2. 中国石化石油物探技术研究院, 南京 211103
2. SINOPEC Geophysical Research Institute, Nanjing 211103, China
0 引 言
曲波(Curvelet)变换是在小波变换(Wavelet)和脊波变换(Ridgelet)基础上发展起来的一种多尺度变换(焦李成和谭山,2003),属于稀疏函数表示理论的范畴,克服了小波变换在表达图像边缘的方向特性等方面的内在缺陷,引入方向参数,在表示二维或更高维数据时表现出很强的方向性特征,使其更适合表现图像的曲线细节特征,并且能同时获得对图像平滑区域和边缘部分的稀疏表达,是一种多分辨、带通、具有方向性的函数分析方法(郑静静等,2009).较之小波变换和脊波变换,它能更好的解决高维函数的特征表示问题,在图像去噪、图像增强、图像融合、图像恢复等方面有极大的优越性,有着良好的发展前景.
从曲波变换提出以来,国内外的学者也做了大量的工作,主要是按照提出者的思路进行了一些方法的试验,在图像处理等方面有了一些初步的应用,在地震资料处理方面主要是地震数据的去噪方面有一些探索性的研究(仝中飞等,2008;张恒磊等,2008).去噪是地震资料处理中的一项重要环节,去噪效果的好坏,将直接影响地震资料的可靠性、参数提取的精度及提高分辨率的效果等,同时也对地震资料的保幅和有效信号的保护有着很大的影响.曲波变换的多尺度和高度各向异性的特点,在地震数据处理领域有着巨大的发展潜力.
目前,曲波变换应用于地震去噪的方法主要是阈值去噪,通过对含噪数据的多尺度曲波变换,利用噪声和有效信号在不同方向和尺度的分布,通过设定一定的阈值条件,将噪声和有效信号进行分离,进而达到去噪效果.本文在曲波变换阈值去噪算法基础上引入循环平移(即Cycle spinning)技术(梁栋,2005;Felix et al., 2008),可以抑制由于变换缺乏平移不变性而产生的伪吉布斯现象(Gibbs-like phenomena),而且可以很好的保留信号,获得更好的去噪效果.
1 曲波变换基本原理
曲波变换最早是由Candès和Donoho(1999)在Ridgelet变换的基础上提出来的.Ridgelet变换也是一种多尺度变换,它为了克服Wavelet变换对自然图像线奇异特性表达不能达到最优化逼近的不足,解决了Wavelet处理高维奇异性带来的问题,但对于含曲线奇异的多变量函数,其逼近性能只相当于Wavelet变换,不具有最优的非线性逼近误差衰减阶.曲波变换具有很强的方向性能够高效地表示图像的边缘,第一代曲波变换(Candès and Donoho, 2000)通过子带分解、平滑分块、正规化和Ridgelet分析等一系列步骤来实现,它的算法的实现较困难,而且曲波变换金字塔式的分解也带来了巨大的数据冗余量,Candès和Donoho又提出了新的曲波变换紧致框架,它是基于频域的曲波变换实现方法,实现更简单、更便于理解,被称为第二代曲波变换(Candès and Donoho, 2005).它直接从多尺度分析理论出发,在频域进行分析实现,通过设计一个特殊的频率窗来进行数值计算,使Curvelet成为真正意义上的多尺度分析法.它减少了实现过程的参数,计算速度更快,冗余量更小,是不连续边缘的优化稀疏表示.新框架曲波变换的提出使得曲波分析理论前进了一大步.Candès等人给出了基于第二代曲波变换理论的快速离散算法——USFFT和Wrapping(Candès et al., 2006),使曲波变换得到快速发展.
1.1 连续曲波变换
连续曲波变换和小波变换、脊波变换理论一样都属于稀疏理论的范畴,采用基函数与信号的内积形式实现信号的稀疏表示,曲波变换可表示为
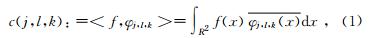
曲波变换在频率域内实现,采用频率域中的窗函数U来实现φ在频率域中的显示.
定义一对窗函数:径向窗函数W(r),r∈(1/2,2)和角度窗函数V(t),t∈[-1,1],它们都满足可允许条件:

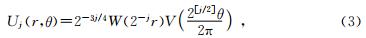
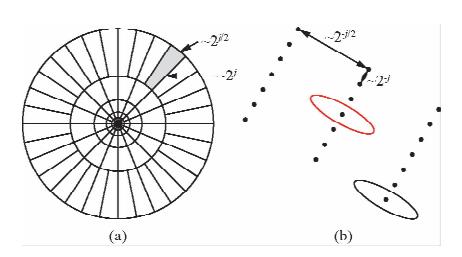 |
图 1 曲波变换的频域和空间域 (a)频域;(b)空间域. Fig. 1 2D curvelet tiling of space and frequency (a)Frequency domain;(b)Frequency domain. |
在连续曲波变换的频率窗定义中,曲波函数的频率域采样是在极坐标系下进行的,而在空间域则采用直角坐标系.实际计算中,采用两种坐标系在频率域和空间域中不能直接计算,用在地震数据分析时就很不方便.因为地震数据在空间域利用直角坐标系,经过傅立叶变换到频率域后,也是直角坐标系,因此,将频率域中的极坐标结构用直角坐标结构来代替处理起来就方便得多,这样,极坐标系中的同心圆环(图 1a)就变为直角坐标系中的同心正方形环,旋转对称被剪切对称所代替,如图 2所示.
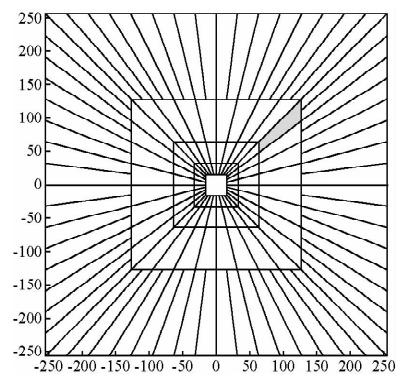 | 图 2 离散曲波变换尺度角度分割示意图 Fig. 2 2D discrete curvelet transform angle and scale division |
以笛卡尔坐标系下的f[t1,t2](0≤t1,t2
离散曲波变换的实现方法有两种快速算法,分别是USFFT算法(Unequispaced fast fourier transforms)和WRAPPING算法(Wrapping-based transform).这里采用基于Wrapping的快速离散曲波变换实现方法,在具体实现时对任意区域,通过周期化技术一一映射到原点的仿射区域.该方法,具体实现过程如下:
(1)对于给定的一个二维函数进行二维快速傅立叶变换,转换到二维频率域:
(2)在频率域,对于每一对(j,l)(尺度,角度),重采样或者插值
(3)用窗函数
(4)围绕原点Wrapping局部化
(5)对每一个
2 基于曲波变换的循环平移阈值去噪方法
在地震勘探中,随机噪声是一种频带较宽的干扰波,常规的去噪方法效果不理想(刘志刚等,2009).曲波变换沿曲线描绘边缘和异常点,可以用很少的系数实现相当准确的重构,而且它具有多尺度特性和良好的方向性,噪声信息和边缘信息能够很好的分开,在噪声抑制方面有很好的优越性.基于曲波变换的阈值去噪(Donoho,1995;Starck et al.,2002),和小波变换的思想一致(Coifman and Donoho, 1995),通过对含噪数据的多尺度曲波变换,利用噪声和有效信号在不同方向和尺度的分布,通过设定一定的阈值条件,将噪声和有效信号进行分离,进而达到去噪效果(姜宇东等,2012),其主要优点是在曲波变换去噪的图像中,不含有基于小波变换的去噪图像中出现的边缘问题.
在阈值去噪过程中,如果变换缺乏平移不变性,就会在有效信号的不连续点相邻位置产生伪吉布斯现象,导致视觉失真,尤其对于图像中的边缘细节部分,伪吉布斯现象尤为明显.循环平移(cycle Spinning)方法就是为了抑制小波变换阈值去噪过程中产生的这一现象提出的(Coifman and Donoho, 1995;梁栋等,2005),曲波变换本身也有这一特性,这里将这一方法引入到曲波变换的地震随机噪声衰减领域,在地震数据随机噪声衰减过程中对含噪信号分块,然后在行和列方向进行“循环平移-阈值去噪-逆向循环平移”.这样每次平移后的信号进行阈值去噪会使伪吉布斯现象出现在不同地方,行和列方向上的次平移处理都会得到一个不同的去噪结果:
对所有去噪结果进行线性平均将得到抑制伪吉布斯现象的去噪结果:
利用cycle spinning方法的计算流程可用图 3表示.主要包括以下几个步骤:
(1)对含噪数据采用循环平移方法(即cycle spinning),即通过一个平移函数对由含噪数据组成的二维矩阵沿行和列方向进行平移,形成新的二维数组,每次移动1行1列.
(2)对得到的二维数组进行Curvelet变换得到曲波系数.
(3)对得到的曲波系数进行阈值去噪得到新的曲波系数.
(4)对得到的新的曲波系数进行Curvelet逆变换得到新的二维数组.
(5)对得到的新的二维数组进行行和列方向的逆向平移,恢复数据原先的状态,即得到一次平移的去噪结果.
(6)判断是否达到设定的循环处理次数,如果达到,则处理完成,转入步骤(7);如果否,则返回步骤(1),这里可以设定最小平移次数为1,最大平移次数为行数×列数. 具体实施时,可以只移动1次,也能达到效果,移动次数越多,去除的信息会越来越多,一般实施时,按最大平移次数进行处理,目的就是让噪声出现在不同的地方进行反复的去噪,得到更好的去噪效果.
(7)对所有去噪结果进行线性平均得到最终去噪结果.
根据以上流程,对地震数据进行随机噪声衰减试验,对地震模拟单炮记录加入白噪声,应用Wrpping算法对含噪数据进行曲波变换,选取合适的阈值条件,通过Cycle Spinning方法进行循环平移再去噪.图 4为对地震单炮记录添加最大值5%的白噪声然后进行去噪的效果.图 5、图 6分别为含不同噪声水平的地震模拟单炮记录的去噪效果.从去噪结果来看,利用循环偏移技术进行阈值去噪,在去除的噪音里几乎看不到有效波成分,去噪对有效信号的保护效果明显.
图 7为地震单炮记录原始数据与去噪结果的频谱对比,从结果来看,基于曲波变换的循环平移阈值去噪方法,对不同含噪能量的地震数据去噪都得到了较好的效果,去掉的噪声中看不到有效波信息,而且去噪前后数据的频谱基本上没有什么变化.
为了进一步探索对于实际地震数据随机噪声衰减效果,选取了一个含随机噪声的地震剖面进行了试验,如图 8所示.从去噪效果来看,随机噪声被有效去除,而且重构的信号很好的保留了图像的边缘信息,断层和同相轴刻画清晰,达到了去噪目的.可见,基于曲波变换的循环偏移阈值去噪方法能够用于随机噪声衰减.
曲波变换是一种新的多尺度几何分析方法,它在地震数据处理中的应用也越来越广泛,对曲波变换的地震数据随机噪声衰减方法进行了探索,利用曲波变换阈值去噪结合循环平移(Cycle spinning)方法提出了基于曲波变换的Cycle spinning的阈值去噪方法,并应用这些方法对地震数据随机噪声衰减进行了研究.得到几点认识:
(1)利用地震记录上有效信号与随机噪声在相关性方面的差异,并且结合曲波变换的多尺度和高度各向异性特征,通过曲波变换可以将地震数据的有效信号和噪音变换到不同的尺度和方向上,利用阈值去噪方法是有效的.
(2)通过引入循环平移(Cycle Spinning)方法,将地震数据分块进行循环平移之后再利用曲波变换阈值去噪方法进行去噪,可以消除伪吉布斯效应,而且从去噪后的视觉效果、去噪前后的频谱分析对比等方面的分析可以看出,这种方法能够得到较好的去噪效果,但由于平移带来了较大的计算量,影响了计算效率.
(3)曲波变换作为一种先进的多尺度变换,目前在图像去噪、图像增强、图像融合、图像恢复等方面优于其它算法,有着良好的发展前景.由于曲波变换的先进思想,针对地震资料处理与解释的曲波变换方法研究将成为地震资料分析领域的一个重要研究方向.
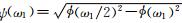 ,定义
,定义

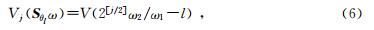
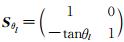 .θl并非等间距的,但是斜率是等间距的.图 2中阴影部分是尺度j=6,l=8时的尺度角度分割.定义
.θl并非等间距的,但是斜率是等间距的.图 2中阴影部分是尺度j=6,l=8时的尺度角度分割.定义
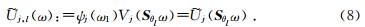
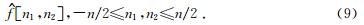
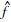 [n1,n2],得到新的采样值:
[n1,n2],得到新的采样值:
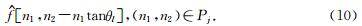
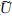 j乘以重采样后的目标函数f,在方位角为θl的平行四边形内局域化f,得到:
j乘以重采样后的目标函数f,在方位角为θl的平行四边形内局域化f,得到: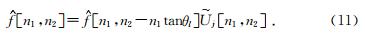
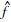 [n1,n2],得到
[n1,n2],得到
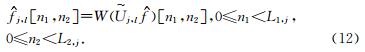
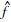 j,l进行二维快速傅立叶逆变换,得到离散的曲波系数集合cD(j,l,k).
j,l进行二维快速傅立叶逆变换,得到离散的曲波系数集合cD(j,l,k).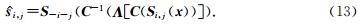

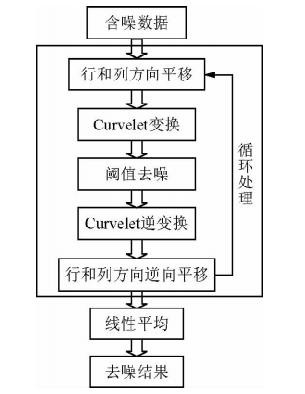
图 3 循环平移方法阈值去噪流程
Fig. 3 Thresholding process using
cycle spinning method

图 4 地震单炮记录循环平移方法阈值去噪(含噪5%)
(a)含噪数据;(b)去噪结果;(c)去除的噪声.
Fig. 4 Seismic thresholding De-noising using cycle spinning method(noisy 5%)
(a)Noisy data;(b)Denoising result;(c)Removed noise.

图 5 地震单炮记录循环平移方法阈值去噪(含噪10%)
(a)含噪数据;(b)去噪结果;(c)去除的噪声.
Fig. 5 Seismic thresholding De-noising using cycle spinning method(noisy 10%)
(a)Noisy data;(b)Denoising result;(c)Removed noise.

图 6 地震单炮记录循环平移方法阈值去噪(含噪15%)
(a)含噪数据;(b)去噪结果;(c)去除的噪声.
Fig. 6 Seismic thresholding De-noising using cycle spinning method(noisy 15%)
(a)Noisy data;(b)Denoising result;(c)Removed noise.
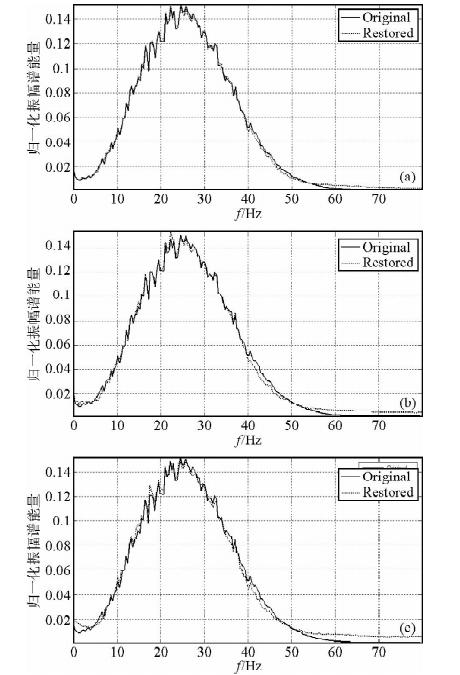
图 7 地震单炮记录原始数据与去噪结果的频谱对比
(a)含噪5%;(b)含噪10%;(c)含噪15%.
Fig. 7 Spectral contrast of seismic original data
and de-noising result
(a)Noisy 5%;(b)Noisy 10%;(c)Noisy 15%.
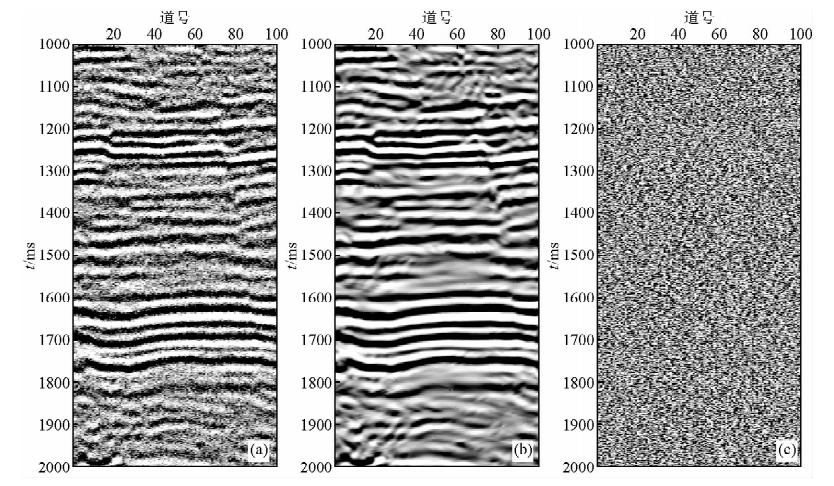
图 8 实际地震剖面随机噪声衰减试验
(a)含噪数据;(b)去噪结果;(c)去除的噪声.
Fig. 8 Field seismic de-noising test using cycle spinning method
(a)Noisy data;(b)Denoising result;(c)Removed noise.
| [1] | Candès E, Donoho D L. 1999. Curvelets[R]. Stanford: Stanford University. |
| [2] | Candès E J, Guo F. 2002. New multiscale transforms, minimum total variation synthesis: applications to edge-preserving image reconstruction[J]. Signal Processing, 82(11): 1519-1543. |
| [3] | Candès E, Donoho D L. 2005. Continuous curvelet transform: I. resolution of the wavefront set[J]. Applied and Computational Harmonic Analysis, 19(2): 162-197. |
| [4] | Candès E, Demanet L, Donoho D, et al. 2006. Fast discrete curvelet transforms[J]. Multiscale Modeling & Simulation, 5(3): 861-899. |
| [5] | Coifman R R, Donoho D L. 1995. Translation-invariant de-noising[A].//Wavelets and Statistics, Springer Lecture Notes in Statistics[C]. New York: Springer-Vedag, 125-150. |
| [6] | Donoho D L. 1995. De-Noising by Soft-thresholding[J]. IEEE Transactions on Information Theory, 41(3): 613-627. |
| [7] | Donoho D L, Duncan M R. 2000. Digital curvelet transform: Strategy, implementation and experiments[A].//Proceeding of SPIE[C]. San Jose, CA: SPIE Press, 12-30. |
| [8] | Herrmann F J, Wang D L, Hennenfent G, et al. 2008. Curvelet-based seismic data processing: A multiscale and nonlinear approach[J]. Geophysics, 73(1): A1-A5. |
| [9] | Starck J L, Candès E J, Donoho D L. 2002. The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing, 11(6): 670-684. |
| [10] | 姜宇东, 杨勤勇, 何柯,等. 2012. 基于曲波变换的地面微地震资料去噪方法研究[J]. 石油物探, 51(6): 620-624. |
| [11] | 焦李成, 谭山. 2003. 图像的多尺度几何分析: 回顾和展望[J]. 电子学报, 31(12A): 1975-1981. |
| [12] | 梁栋, 沈敏, 高清维,等. 2005. 一种基于Contourlet递归Cycle Spinning的图像去噪方法[J]. 电子学报, 33(11): 2044-2046. |
| [13] | 刘志刚, 谢言光, 陈峰. 2009. 地震数据处理中噪声衰减方法的探讨[J]. 石油地球物理勘探, 44(S1): 67-71. |
| [14] | 张恒磊, 张云翠, 宋双,等. 2008. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 43(5): 508-513. |
| [15] | 郑静静, 印兴耀, 张广智. 2009. 基于Curvelet变换的多尺度分析技术[J]. 石油地球物理勘探, 44(5): 543-547. |
| [16] | 仝中飞, 王德利, 刘冰. 2008. 基于Curvelet变换阈值法的地震数据去噪方法[J]. 吉林大学学报(地球科学版), 38(sup.): 48-52. |
 2015, Vol. 30
2015, Vol. 30

