2. 中国石化胜利油田物探研究院, 东营 257000
2. Shengli Oilfield Geophysical Institute, Dongyin 257000, China
0 引 言
地震波的传播速度是地震勘探中的一个基本参数,在地震资料处理和地震解释的诸多环节中扮演着重要的角色.影响地震波传播速度的因素有很多,诸如地下介质的岩性、密度、孔隙度、埋藏深度等等,这些因素最终体现在地震波的走时、波形、振幅和相位等属性上变化.只有充分了解速度及影响因素的相互关系,才有可能更为准确地估计出地下的结构和构造.全波形反演是利用全波场的正演模拟技术,通过正演得到地震记录与实际野外观测记录进行匹配,以数据残差最小化为目标函数,利用最优化方法进行迭代求解的方法.全波形反演因其利用走时、波形、振幅等信息进行反演而具有高分辨率的特性.
全波形反演从20世纪80年代开始,主要经历了三个阶段:第一阶段为全波形反演理论建立和验证阶段.时间域全波形反演的理论框架最先由Lailly、Tarantola等人于20世纪80年代建立,其基本思想为利用波动方程进行正演获得初始的地震记录,通过进行正演数据与观测数据之间的匹配来获得波场残差,利用以波场残差为震源进行波场逆时外推,通过正传波场与残差波场逆时外推的波场进行互相关构建梯度算子,以获得迭代更新方向(Lailly,1983; Tarantola,1984; Gauthier et al., 1986; Kolb et al., 1986; Mora,1987).第二阶段为全波形反演理论发展阶段,其中以频率域的全波形反演为代表:Pratt等人将时间域残差反传的思想引入频率域,在单频的地震数据内进行波形匹配,简历了完善的频率域全波形反演理论.相比于时间域,频率域全波形反演可利用低频向高频的反演策略实现多尺度反演,以减弱全波形反演中强烈的非线性(Pratt,1999; Sirgue and Pratt, 2004).自21世纪初至今,全波形反演达到了蓬勃发展的阶段,全波形反演因其高分辨率的特点受到学者关注,其理论算法也逐步从二维反演走向三维反演,从声波走向弹性波反演,从单参数反演走向多参数反演,从理论模型验证到实际资料的反演(Shin and Cha, 2007;Ben-Hadj-Ali et al., 2008; Shin and Cha, 2008; Virieux and Operto, 2009;卞爱飞等,2010; Warner et al., 2013; 陈永芮等,2013;董良国等;2013;高凤霞等,2013;刘璐等,2013;任浩然等,2013;曹书红和陈景波,2014).
全波形反演利用的是叠前地震记录,通过匹配地震数据进行反演,不仅利用了地震信号的走时,而且还利用了地震信号的振幅值信息,理论上具有较高的分辨率的优秀特性.但是全波形反演也存在难以克服的缺点:(1)在反演过程中需要多次求解波动方程,需要巨大的数据运算和海量数据读写,在时间域全波形反演需要读取、保存全波场的地震数据,对数据I/O要求较高,在频率域的全波形反演需要求解大型稀疏矩阵,对计算机硬件内存要求较高(殷文等,2008;廖建平等,2011);(2)全波形反演是大规模的非线性反演问题,反演过程中非线性强烈,对初始速度较为敏感,当初始速度模型较差或者地震信号中缺失低频信号时,反演过程中会陷入局部极值(杨午阳等,2013).
时间域全波形反演在迭代反演过程中,需要求取目标函数的梯度算子,梯度算子和逆时偏移算法相近,构建都需要主要分为三步:(1)利用地震正演进行求解震源子波的正传波场;(2)以波场残差为震源求解逆时反传波场;(3)两波场互相关构建梯度算子.因为求解正演波场的时间顺序和求解残差的反演波场的时间顺序相反,必须先在磁盘中保存所有的正演全波形地震数据,其数据读写量大,效率低.针对数据运算量大的缺点,学者也给出不同的优化算法:如逆时偏移过程中的随机边界算法和Nguyen等人的激发振幅成像条件等算法.随机边界算法是通过保存边界处的波场值,在检波器点处的波场逆时反传的同时进行震波波场的重建,随机边界的思想是通过增加计算量来减少数据的读写(Clapp,2009).Nguyen和McMechan提出基于稳定激发振幅成像条件则是利用激发最大振幅值进行波场成像,从而避免了硬盘存储和减少了I/O吞吐(Nguyen and McMechan, 2012;张智等,2012).本文针对时间域梯度算子数据量大的问题,提出了特征能量梯度公式,用以解决反演中过程中梯度算法数据读写量大的缺点.文章首先介绍了全波形反演的基本原理和梯度算子的表达式;第二部分介绍了特征能量梯度算法的原理;第三部分将通过Marmousi模型来和实际资料的反演来验证优化算法的计算精度和求解效率;最后给出结论和认识.
1 全波形反演核心内容
1.1 目标函数
全波形反演是基于波场残差最小平方的非线性反演问题,首先建立目标函数目E(m):正演地震记录与野外观测地震记录的波场残差的L2模为
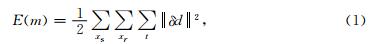
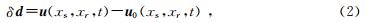
1.2 时间域梯度算子
全波形反演的目标是通过求取合理的模型参数m使得波场残差值的最小,在数学上属于非线性、无约束、多参数的最优化问题,一般的求取方法采用无约束的局部最优化方法进行迭代求解,如梯度类算法和牛顿类算法.其中基于最速下降法属于梯度类算法,其迭代更新公式为

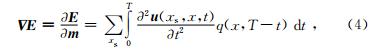
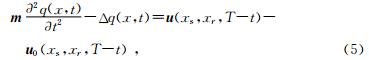
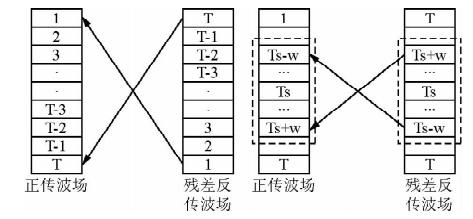 |
图 1 构建梯度算子示意图 (a)常规梯度算法;(b)特征能量梯度算法. Fig. 1 Illustration of Gradient algorithm (a)Conventional gradient equation; (b)Eigen energy gradient equation. |
由公式(4)梯度公式可知:梯度是由震源激发正传波场的二阶偏导与波场反传为震源的波场反传波场关于时间t的互相关构成的.互相关的总的时间长度为正演波场的总时间长度T.但在构建梯度算子过程中,不同时刻的波场值对梯度算子的贡献度是不同的,越靠近波前面的波场值对梯度算子的贡献度越大,所以在构建梯度算子过程中,无需保存全波场的地震数据,只需要保存对于梯度算子贡献较大的波场值,然后在波场残差反传过程中,抽取向对应时刻的波长值进行构建梯度算子.基于此思想,本文提出特征能量梯度算子,首先定义特征能量:
在时间维度上,两波场并非所有的时间上都构成梯度算子,而是主要集中在以正传波场的最大特征能量值的为中心的一段时间段内,即正传波场的特征能量.定义每个正演网格点上最大激发特征能量值Emax为
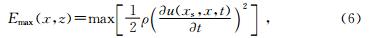
其中ρ为介质密度,最大特征能量Emax对于的时间步为Ts.
特征能量梯度算法是计算正传波场时,计算每一个空间网格点上的最大激发能量强度,以及最大能量强度对应时间步Ts,保存以该时间步为中心的一个时窗长度2×w内所有的激发振幅值,这些振幅集中了震源激发波场传播的特征能量;然后在计算波场误差反传时,寻找到最大振幅对应的时间步与当前时刻相等的网格点空间坐标,并将该点在最大振幅对应的时间步对应时窗内的波场误差反传波场、激发最大振幅值、以及相应系数相乘并求和,就得到该点的梯度.公式为
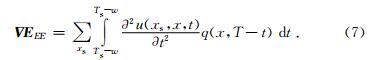
特征能量梯度算法实现的步骤:
(1)估算构建特征能量梯度的长度和时间;
(2)在正传波场中计算每个网格点上的波场能量值,保存特征能量长度2w内的波场值,以及最大特征能量值Emax对应的时间步Ts;
(3)在波场残差反传中,根据各个网格点的特征能量时间步Ts,保存特征能量长度内的误差反传的波场值;
(4)根据公式特征能量优化梯度算子计算梯度.
常规梯度算法利用保存全部时刻的正传波场记录,利用互相关条件与残差反传波场进行互相关成梯度,如图 1a所示,利用的波场数据量为全波场时间长度T的数量级.特征能量梯度算法通过估算特征能量出现的时间步Ts,估算特征能量延续的时间长度,利用特征能量互相关构建梯度,如图 1b虚线所示,利用的波场数据量为子波长度2 w的数量级.
特征能量梯度算子的精度依赖于特征能量的时间长度,当选取的特征能量较长时候,构建的梯度算子的精度越高,当特征能量的时间长度选择为总的正演时间长度的时候,特征能量梯度算法就等于常规梯度算法.为了验证特征能量的精度,设计了平层速度进行对比常规梯度算法和特征能量算法,图 2a为真实速度模型,三层的速度分别为2 km/s、3 km/s、4 km/s,选取平滑的背景速度作为反演的初始速度模型.图 2.b为利用的常规梯度算法求出的梯度算子,梯度算子的数量级为[-4e-5,6e-5].本文分别选取了特征能量时间点数为25和101进行梯度测试,其构建梯度算子分别如图 2c、d所示.从图中可知,时间长度选取25个点时,特征能量构建的梯度形态与常规梯度算子总体一致,但是数量级在[-2e-6,6e-6]之间,当是当特征能量时间长度延长至101点时,梯度算子的数量级和形态与常规梯度算子一致.
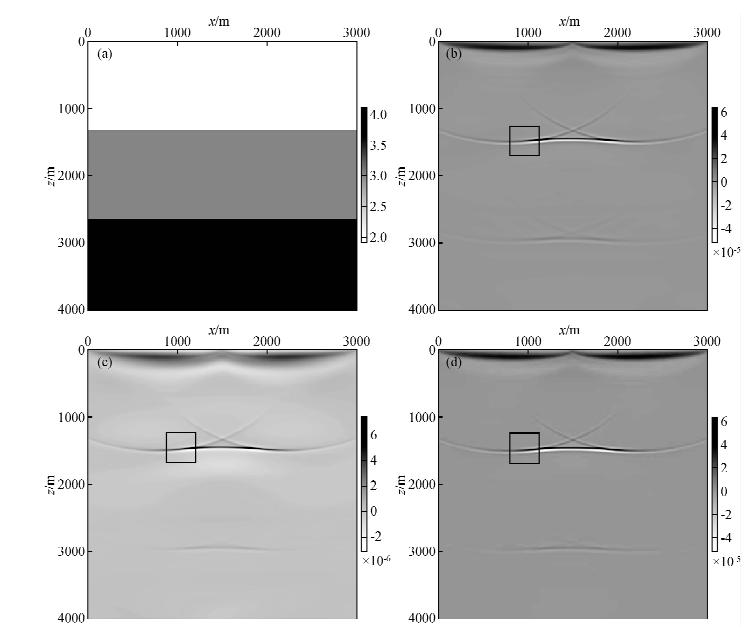 |
图 2 简单速度模型测试 (a)平层速度模型,单位为[km/s];(b)利用常规梯度算法求解的梯度; (c)利用时间长度25个点构建提算子的特征 能量梯度算法求解梯度;(d)利用时间长度101个点构建提算子的特征能量梯度算法求解梯度. Fig. 2 A simple test (a)Velocity model;(b)Conventional gradient method;(c)Eigen gradient method using 25 points; (d)Eigen gradient method using 101 points. |
图 3为抽取的单道梯度对比图,从图中也能发现当特征能量时间长度较短时,构建的梯度算子能量较弱,与真实梯度算子相差较大,当梯度算子较长时,构建的梯度算子越符合真实梯度算子.本文通过验证了当特征能量时间长度选取为一个子波周期的延续时,特征能量梯度算子可以满足精度需求.
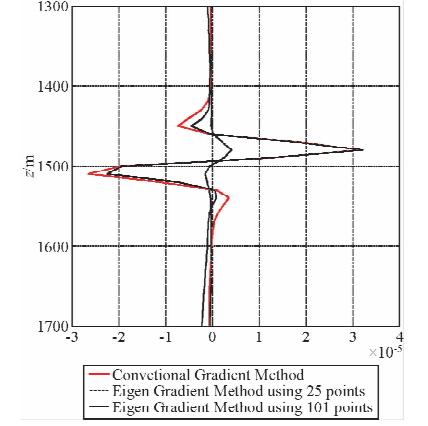 | 图 3 单道梯度算子对比图 Fig. 3 Illusion single trace of gradient |
红线为常规梯度算法;黑色破折线为时间长度25个特征能量梯度算子;黑色实线为时间长度101个特征能量梯度算子.
2 Marmousi模型测试
为测试特征能量梯度算法在复杂模型中的精度,设计了的Marmousi模型的反演梯度试验:模型的网格点数为:1501×401,网格间距为10 m.单炮的检波线长度为3000 m,震源 点中间激发,检波器双边接收,炮数为43炮,炮间隔为50 m,时间采样点数为6001,时间采样间隔为0.4 ms,反演利用的速度模型为平滑过后的Marmousi模型,如图 4a、b所 示.震源子波选取的为20 Hz雷克子波,其子波周期为0.05 s,则特征能量的时间长度为125个时间点.
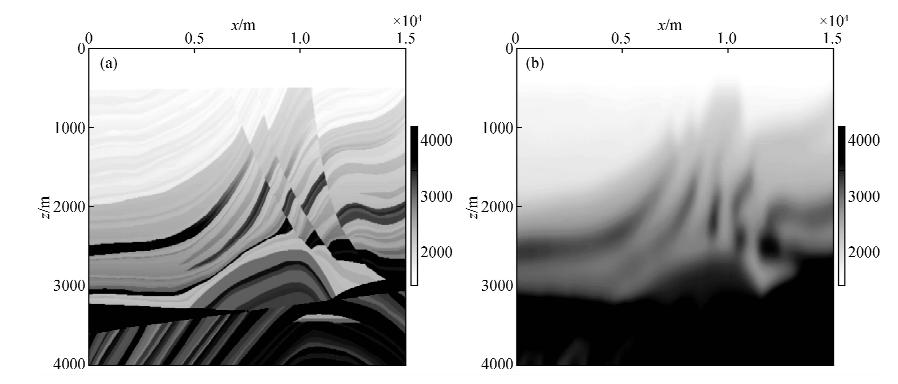 |
图 4 Marmousi速度模型 (a)平滑初始速度模型;(b)真实速度模型. Fig. 4 Marmousi velocity model (a)Smoothed velocity for initial iteration;(b)True velocity model. |
利用特征能量梯度算法进行全波形反演,对比与常规梯度算法的梯度求取结果:首先根据真实的速度模型进行有限差分正演,获得实际野外的观测地震记录,然后利用平滑的速度模型进行全波形反演.其中图 4a为真实的Marmousi模型,b为平滑的Marmousi模型.平滑模型作为全波形反演的初始速度模型.在全波形反演过程中,通过初速模型模型正演获得地震观测记录与实际野外观测记录的进行匹配,获得波场残差值,如图 5a、b所示.特征能量梯度算法在求取正演波场时,利用公式(6)计算每一个网格点上的激发能量值,求取每个网格点的最大激发特征能量值以及最大激发特征能量值对应的时间步,如图 6a、b所示.
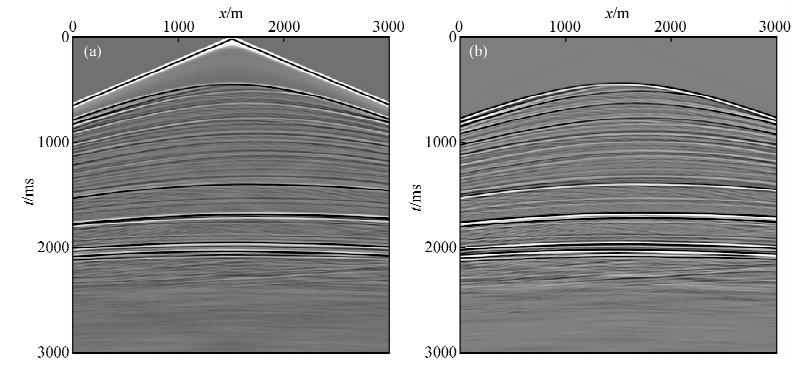 |
图 5 Marmousi第10炮地震记录 (a)反演的观测地震记录;(b)反演过程中的波场残差记录. Fig. 5 No 10 shot’s seismic record (a)Oberved record;(b)Residual data. |
 | 图 6(a)单炮Marmousi模型的激发最大特征能量分布;(b)激发最大特征能量对应的的时间步. Fig. 6 Single-shot marmousi velocity test (a)Max eigen energy;(b)Corresponding time step. |
为说明特征能力梯度的精度问题,分别对比单炮Marmousi梯度和多炮Marmousi梯度.图 7为第10炮的单炮梯度测试结果,其中图a为单炮内计算的最大激发振幅值;图b为激发振幅值所对应时间步,单位为ms;图c为利用公式(4)常规梯度算法计算的单炮Marmousi梯度;图d为利用公式(6)特征能量梯度算法计算的梯度.
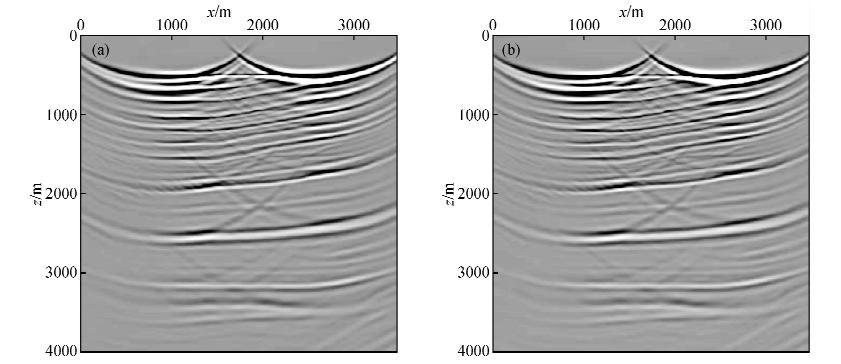 |
图 7 Marmousi单炮梯度对比图 (a)常规算法求取梯度;(b)特征能量算法求取梯度. Fig. 7 The single shot gradient of marmousi model (a)Gradient using conventional equation;(b)Gradient using eigen energy gradient equation. |
图 8为多炮Marmousi梯度对图比,图a为常规梯度,图b为特征能量梯度,为对比二者的精度,进行归一化作差,二者的相对差值均在3%以内.
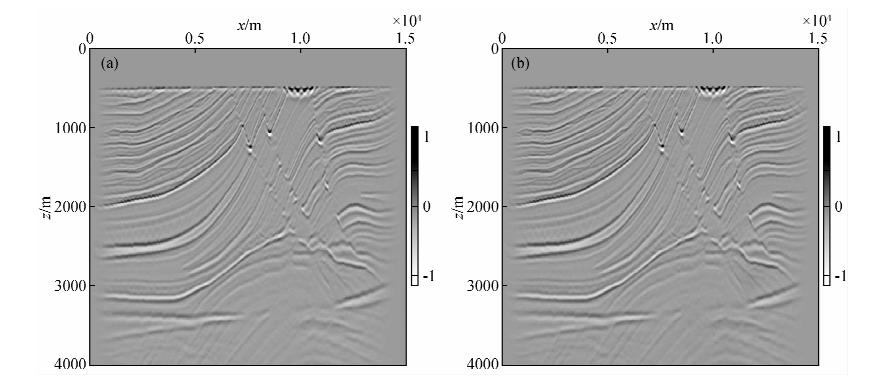 |
图 8 Marmousi多炮梯度对比图 (a)常规算法求取梯度;(b)特征能量算法求取梯度. Fig. 8 The multishot shot gradient of marmousi model (a)Gradient using conventional equation;(b)Gradient using eigen energy gradient equation. |
在I/O数据吞吐量上,因为特征能量梯度算法构建梯度算子仅仅利用了一个地震子波延续时间的时间长度的波场进行构建梯度,数据量大大的减少.表 1是统计Marmousi模型中单炮数据和多炮数据的数据吞吐量.特征能量梯度算法I/O吞吐量是仅为常规梯度算法的46分之一,可以减少I/O吞吐时间,提高反演的效率.
|
|
表 1 Marmousi模型I/O吞吐数据量统计 Table 1 The statistic for Input/Output date in Marmousi velocity |
为了验证特征能量梯度算法在实际资料中的效果,本文对胜利某工区的实际地震资料进行反演.从三维观测系统中抽取的一条二维线进行反演,反演工区大小为25600 m,地震资料的炮数为128炮,双边检波器接收,单边最大偏移距为4000 m.采取的正演算法是常规网格10阶的有限差分正演算法,选取的PML吸收边界条件.通过频谱分析,地震子波的优势频带在10~25 Hz,则子波选取的为20 Hz的雷克子波,为保证激发振幅特征能量梯度算法的精度,时窗长度选取150 ms.
硬件信息为:服务器型号R910,CPU为Intel Xeon E7-4830,主频2.13 GHz,内存容量为126 GB,软件编译环境为RHL5.5系统,C语言编译器为:icc.利用常规的梯度算法是迭代一次耗时时间约为320 min.利用OpenMP并行API接口,开辟32个线程,并行策略为:利用OpenMP开辟多线程进行单炮梯度并行计算,每一线程分别进行计算正传波场、计算波场残差、波场残差反传以及求取单炮梯度,如图 6所示.
图 10为两者算法的在第一次迭代的梯度对比图;图 11为不同迭代次数的波形对比图,其中左图为实际观测记录,右图为不同迭代速度模型的正演模型;图 9为两种算法的误差下降曲线对比图;图 12为反演的初始速度模型.图 13为反演的最终结果.
 | 图 9 基于特征能量梯度算法并行计算流程图 Fig. 9 Workflow of FWI in one iteration: for shot loop we use OpenMP to create thread parallel and for gradient calculation we use excitation main energy gradient equation |
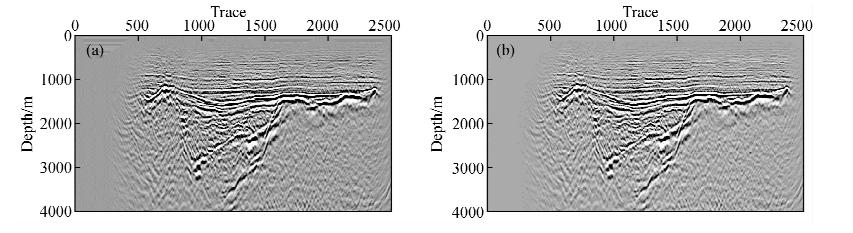 |
图 10 实际资料的第一次迭代梯度对比图 (a)常规算法求取梯度;(b)特征能量算法求取梯度. Fig. 10 The first iteration gradient comparison (a)Gradient using conventional gradient equation;(b)Gradient using excitation main energy gradient equation. |
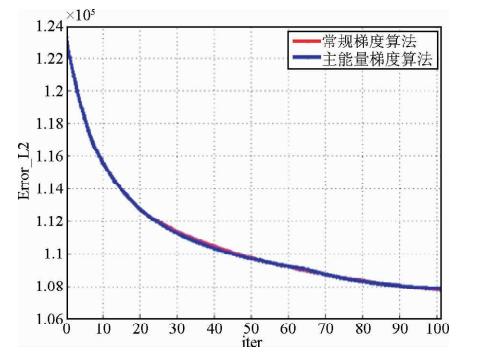 | 图 11 误差下降曲线图,常规梯度算法(红线), 特征能量梯度算法(黑线) Fig. 11 Convergence curve of residual error function conventional gradient equation(red line),excitation main energy gradient equation(black line) |
 |
图 12 特征能量梯度算法在不同迭代次数的波形匹配图
左图为实际地震记录,右图为正演地震记录 (a)第1次迭代;(b)第50次迭代;(c)第100次迭代. Fig. 12 The waveform comparison in different iteration,the left is real seismic record and the right is modeling seismic record (a)1th iteration;(b)50th iterations;(c)100th iterations. |
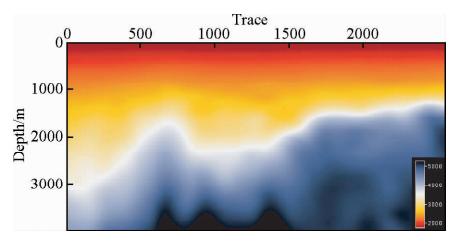 | 图 13 反演初始速度模型 Fig. 13 Initial velocity model |
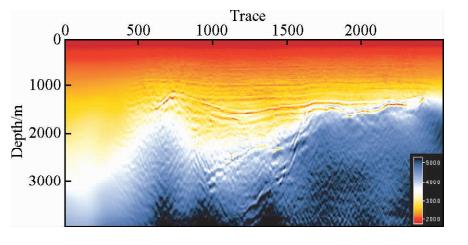 | 图 14 最终反演结果 Fig. 14 Inversion velocity model |
实际资料的效率分析:在大模型的全波形反演中,数据的读写占据了大部分时间,数量级达到数百Gb甚至是Tb级别. 表 2是基于实际资料的两种算法的数据对比,在常规梯度算法中每迭代I/O吞吐量为968 Gb.在全波形反演程序中读写968 Gb数据占据了迭代一次时间的76%,严重消耗时间.基于特征能量梯度算法是不保存全部的波场值,只保存构建梯度的关键特征波场值,将数据吞吐量减少到了64 Gb,减少了程序运行中的数据的读写,效率提高了3倍左右.
|
|
表 2 两种算法的数据对比 Table 2 The time consume for gradient methods |
4.1 本文研究了特征能量梯度优化算法,并应用于理论模型测试和实际地震资料的反演,通过理论模型测试表明:优化梯度算法与常规梯度算法相比,精度满足需求;通过实际资料的测试表明:在反演大模型过程中,特征能量梯度算法可以有效的减少I/O吞吐,缩短数据读写时间,提高了计算效率.该算法将构成梯度的数据量从总的时间长度减少到一个子波时间长度,减少数据读写时间.
4.2 本文实现了时间域全波形反演算法,并将算法运用到了实际资料反演.在处理实际中,全波形反演存在诸多问题,如正演算子精度问题、初始速度来源问题、实际野外地震资料预处理问题、周波跳跃问题、效率问题等等.针对效率问题,本文利用优化算法,在保证精度的情况下,提升了反演效率.
致 谢 感谢审稿专家和编辑部的帮助和支持.| [1] | Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Goephys. (in Chinese), 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [2] | Cao S H, Chen J B. 2014. Studies on complex frequencies in frequency domain full waveform inversion[J]. Chinese J. Geophys. (in Chinese), 57(7): 2302-2313, doi: 10.6038/cjg20140724. |
| [3] | Chen Y R, Li Z C, Qin N, et al. 2013. Full waveform inversion with wave equation bi-directional illumination optimization[J]. Progress in Geophys. (in Chinese), 28(6): 3015-3021, doi: 10.6038/pg20130624. |
| [4] | Clapp R G. 2009. Reverse time migration with random boundaries[C]. SEG Technical Program Expanded Abstracts, 28: 2809-2813. |
| [5] | Dong L G, Chi B X, TAO J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion[J]. Chinese J. Geophys. (in Chinese), 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [6] | Gao F X, Liu C, Feng X, et al. 2013. Comparisons and analyses of several optimization methods in the application of frequency-domain full waveform inversion[J]. Progress in Geophys. (in Chinese), 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [7] | Gauthier O, Virieux J, Tarantola A. 1986. Two-dimensional nonlinear inversion of seismic waveforms; Numerical results[J]. Geophysics, 51(7): 1387-1403. |
| [8] | Kolb P, Collino F, Lailly P. 1986. Pre-stack inversion of a 1-D medium[J]. Proceedings of the IEEE, 74(3): 498-508. |
| [9] | Lailly P. 1983. The seismic inverse problem as a sequence of before-stack migrations[M].//Conference on Inverse Scattering: Theory and Applications. Society for Industrial and Applied Mathematics. Philadelphia: SIAM, 206-220. |
| [10] | Liao J P, Liu H X, Wang H Z, et al. 2011. Study on rapid highly accurate acoustic wave numerical simulation in frequency space domain[J]. Process in Geophys. (in Chinese), 26(4): 1359-1363, doi: 10.3969/j.issn.1004-2903.2011.04.029. |
| [11] | Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese J. Geophys. (in Chinese), 56(7): 2447-2451, doi: 10.6038/cjg20130730. |
| [12] | Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 52(9): 1211-1228. |
| [13] | Nguyen B D, McMechan G A. 2012. Excitation amplitude imaging condition for prestack reverse-time migration[J]. Geophysics, 78(1): S37-S46. |
| [14] | Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 167(2): 495-503. |
| [15] | Pratt R G. 1999. Seismic waveform inversion in the frequency domain; Part 1, Theory and verification in a physical scale model[J]. Geophysics, 64(3): 888-901. |
| [16] | Ren H R, Huang G H, Wang H Z, et al. 2013. A research on the Hessian operator in seismic inversion imaging[J]. Chinese J. Geophys. (in Chinese), 56(7): 2429-2436, doi: 10.6038/cjg20130728. |
| [17] | Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 173(3): 922-931. |
| [18] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 69(1): 231-248. |
| [19] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49(8): 1259-1266. |
| [20] | Virieux J, Operto S. 2009. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 74(6): WCC1-WCC26. |
| [21] | Warner M, Ratcliffe A, Nangoo T, et al. 2013. Anisotropic 3D full-waveform inversion[J]. Geophysics, 78(2): R59-R80. |
| [22] | Yang J Z, Liu Y Z, Dong L G. 2014. A multi-parameter full waveform inversion strategy for acoustic media with variable density[J]. Chinese J. Geophys. (in Chinese), 57(2): 628-643, doi: 10.6038/cjg20140226. |
| [23] | Yang W Y, Wang X W, Yang X S, et al. 2014. The review of seismic full waveform inversion method[J]. Process in Geophys. (in Chinese), 28(2): 766-776, doi: 10.6038/pg20130225. |
| [24] | Zhang Z, Liu Y S, Xu T, et al. A stable excitation amplitude imaging condition for reverse time migration in elastic wave equation[J]. Chinese J. Geophys. (in Chinese), 56(10): 3523-3533, doi: 10.6038/cjg20131027. |
| [25] | Yin W, Yin X Y, Wu G C, et al. 2006. The method of finite difference of high precision elastic wave equations in the frequency domain and wave_field simulation [J]. Chinese J. Geophys. (in Chinese), 49(2): 561-568. |
| [26] | 卞爱飞, 於文辉, 周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [27] | 曹书红, 陈景波. 2014. 频率域全波形反演中关于复频率的研究[J]. 地球物理学报, 57(7): 2302-2313, doi: 10.6038/cjg20140724. |
| [28] | 陈永芮, 李振春, 秦宁,等. 2013. 波动方程双向照明优化的全波形反演[J]. 地球物理学进展, 28(6): 3015-3021, doi: 10.6038/pg20130624. |
| [29] | 董良国, 迟本鑫, 陶纪霞,等. 2013. 声波全波形反演目标函数性态[J]. 地球物理学报, 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [30] | 高凤霞, 刘财, 冯晅,等. 2013. 几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J]. 地球物理学进展, 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [31] | 廖建平, 刘和秀, 王华忠,等. 2011. 快速高精度的频率空间域声波数值模拟方法研究[J]. 地球物理学进展, 26(4): 1359-1363, doi: 10.3969/j.issn.1004-2903.2011.04.029. |
| [32] | 刘璐, 刘洪, 张衡,等. 2013. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 56(7): 2447-2451, doi: 10.6038/cjg20130730. |
| [33] | 任浩然, 黄光辉, 王华忠,等. 2013. 地震反演成像中的Hessian算子研究[J]. 地球物理学报, 56(7): 2429-2436, doi: 10.6038/cjg20130728. |
| [34] | 杨积忠, 刘玉柱, 董良国. 2014. 变密度声波方程多参数全波形反演策略[J]. 地球物理学报, 57(2): 628-643, doi: 10.6038/cjg20140226. |
| [35] | 杨午阳, 王西文, 雍学善,等. 2013. 地震全波形反演方法研究综述[J]. 地球物理学进展, 28(2): 766-776, doi: 10.6038/pg20130225. |
| [36] | 张智, 刘有山, 徐涛,等. 2013. 弹性波逆时偏移中的稳定激发振幅成像条件[J]. 地球物理学报, 56(10): 3523-3533, doi: 10.6038/cjg20131027. |
| [37] | 殷文, 印兴耀, 吴国忱,等. 2006. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 49(2): 561-568. |
 2015, Vol. 30
2015, Vol. 30

