0 引 言

地震数值模拟技术在复杂油气藏地震勘探开发中起着至关重要的作用.近年来，相继在四川盆地川东地区发现了以孔隙裂缝型碳酸盐储层为主的大型构造-岩性-成岩圈闭的天然气藏(郭一华，1994)，在塔里木盆地塔中地区发现了中-古生界以溶蚀缝洞型为主的塔中油气藏等(李延钧，1998)，这些油气藏的发现为我国构造岩性复合型勘探带来新的研究机遇.而伴随而来的是对地震波数值模拟技术提出更为严峻的考验，传统的地震波数值模拟技术一般基于均匀介质或者层状介质的弹性理论进行分析，在解决复杂的非均质性强的介质时会出现一定的局限性，因此需要提出新的地震波数值模拟技术以适应这一要求.

在地震波数值模拟中，有限差分数值模拟方法是应用最为普遍的方法(冯英杰等，2007).Alterman和Karal(1968)最早提出有限差分数值模拟方法；Madariaga(1976)进一步提出了交错网格方法，并将其应用于弹性介质、使得差分精度提高为O(Δt²+Δx²)；Virieux(1984，1986)利用交错网格有限差分方法成功实现了各向同性介质中的SH 波和P-SV波的模拟；董良国等(2000)详细阐述了一阶速度应力方程交错网格高阶有限差分的实现方法，从理论上证明了交错网格具有较高的计算精度和计算效率.以上研究都是基于规则网格的，对于非均匀小尺度介质进行模拟，为了避免因规则网格过采样导致计算效率低等问题，Moczo(1989)首先提出可变网格的有限差分思想来提高数值模拟效率；Jastram和Behle(1992)，Jastram和Tessmer(1994)提出了可变网格的网格 步长可取任意倍数算法；朱生旺和魏修成(2005)利用插值方法实现了变网格有限差分数值模拟的研究，在保证计算精度的条件下较大的提高了地震波数值模拟的效率；孙成禹等(2008)利用传统常规网格有限差分算法和变网格有限差分算法模拟了近地表低速层和地层中夹有低速层两种地层模型，模拟结果表明变网格有限差分算法不仅提高了模拟分辨率而且也提高了计算效率；杜启振等(2010)将强、弱两种约束条件引入交错网格空间离散差分算子，对差分算子通过求取条件极值的方法进行了优化；胡英等(2012)以BISQ模型基本方程为基础，推导出了完全匹配层(PML)吸收边界的交错网格高阶有限差分方法的表达式.

本文在前人研究的基础上，为了避免插值因素导致计算效率低以及引入的额外计算误差等问题，对可变网格有限差分算法进行了改进，并建立了不同的介质模型验证模拟结果的有效性，从而解决了模拟精度和计算效率不能均衡的缺陷，进一步增强了地震波数值模拟技术对小尺度非均质介质的适应性.

1 变网格基本原理

1.1 多尺度网格离散策略

在地震波数值模拟过程中，首先需做的是利用网格对速度场进行剖分.常规网格一般采用单一尺度网格剖分方式，而为了满足复杂介质的多尺度网格离散需求，一般可以采用包含大尺度、小尺度两个区域的速度场来进行离散(如图 1a所示).采用高阶有限差分进行数值模拟时需作插值处理解决大小尺度网格边界问题，而插值处理一方面降低数值模拟效率，另一方面插值势必会引起一定的计算误差积累，影响数值模拟的精度.为了避免上述后果，本文采用改进的速度场剖分方式(如图 1b所示)，将全局速度场剖分分为Ⅰ、Ⅱ、Ⅲ三个尺度的区域(Ⅰ小尺度区域、Ⅱ大尺度区域、Ⅲ过渡带区域)，这样进行高阶差分数值模拟时就可以消除插值因素的影响，使得模型能够自然逐渐过渡、增加数值模拟过程的稳定性.

图 1

Fig. 1

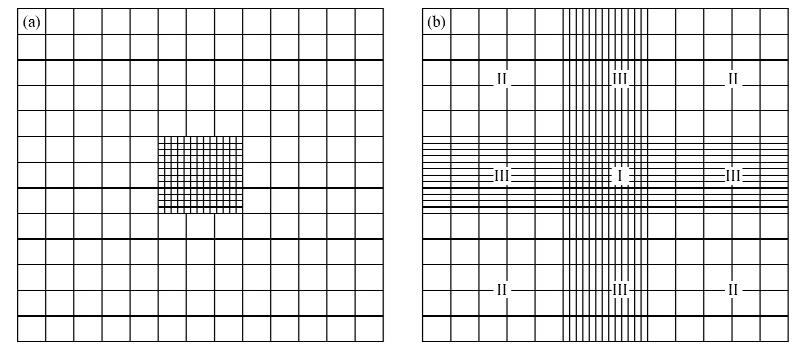图 1 速度场的离散方式 Fig. 1 The discrete way of velocity fields

目前，交错网格算法是有限差分数值模拟中最好的方法之一(董良国等，2000；裴正林和牟永光，2003；裴正林，2004；张建磊等，2008；孟凡顺等，2013)，因此本文以交错网格为例说明可变网格的实现方法.图 2为可变交错网格在过渡区网格差分处理方式示意图(以网格半节点导数差分为例)，为了保证大小尺度网格过渡带所有半节点导数不用插值就可以求其高阶差分数值，不难看出大小尺度网格步长必须为奇整数倍，假设大小尺度网格步长比为l，以网格步长比l=3为例给出可变交错网格的高阶差分算法.这样，高阶有限差分算法以速度场剖分方式为依据，分为三种情况：(1)大尺度网格区域内部；(2)小尺度网格区域内部；(3)大小尺度网格过渡区内部.

图 2

Fig. 2

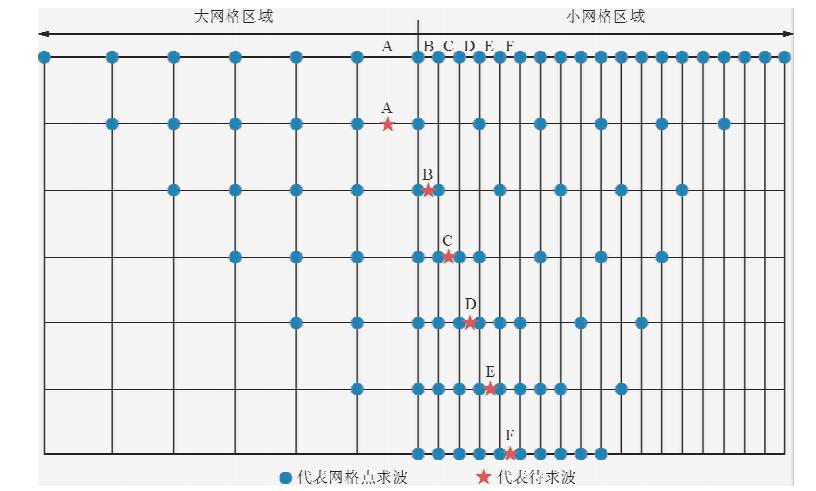图 2 可变交错网格过渡区网格差分处理方式示意图 Fig. 2 The schematic diagram of grid finite difference approach in the variable staggered grid transition zone

大尺度网格区域内部一阶导数∂u/∂x的高阶差分计算公式为

表 1(Table 1)

表 1 可变交错网格过渡带对应的10阶精度的差分系数(粗细比3:1) Table 1 The differential coefficient of 10 order accuracy in the variable staggered grid transition zone(thickness ratio 3:1) 过渡带 所处位置 C′1 C′2 C′3 C′4 C′5 A 0.4037 -2.991E-2 4.614E-3 -5.885E-4 3.956E-5 B 1.0314 -5.262E-2 4.818E-4 -4.478E-5 2.763E-5 C 1.1467 -4.984E-2 3.323E-3 -1.424E-5 5.284E-6 D 1.1857 -7.260E-2 6.467E-3 -2.727E-4 4.477E-6 E 1.2034 -8.423E-2 1.123E-2 -9.823E-4 1.826E-4 F 1.2112 -8.972E-2 1.384E-3 -1.766E-3 1.186E-4

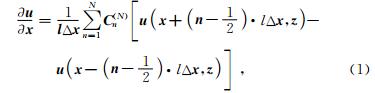
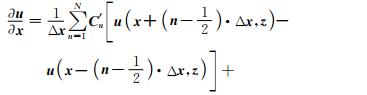
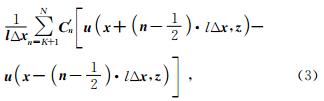
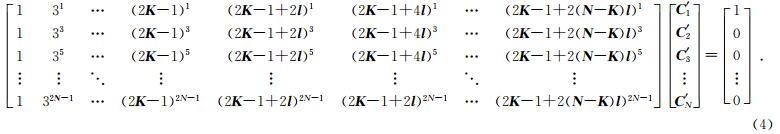
表 1 可变交错网格过渡带对应的10阶精度的差分系数(粗细比3:1) Table 1 The differential coefficient of 10 order accuracy in the variable staggered grid transition zone(thickness ratio 3:1)

在地震波数值模拟中，有限差分模拟存在两大问题：一是吸收边界问题，二是数值频散问题.在高阶有限差分数值模拟中，由于实际介质的无限性，计算的有限性决定了在数值模拟时必然引入人工边界反射问题.本文采用完全匹配层吸收边界条件(PML)实现对可变网格数值模拟的边界处理，根据完全匹配层(PML)吸收边界原理和参量的分裂思想，在不同的方向分别加相应的阻尼衰减因子，解决边界的反射问题.可变网格PML吸收边界同样按照速度场离散方式采用多尺度网格进行剖分，实现方式同交错网格PML吸收边界相似(董良国，1999；王永刚等，2007；杜启振和李宾，2009；李文杰等，2009；孙林洁和印兴耀，2011；刘有山等，2013)，在此不再赘述.

其次，数值频散问题是由单一波长内空间采样数过少产生的，这是因为高阶差分方程离散化后近似连续导数的波动方程时会使得相速度变成空间离散间隔和时间步长的函数(蔡其新等，2003；薛东川和王尚旭，2008；孙成禹等，2009).图 3为空间差分精度分别为4阶、6阶时不同纵横网格间距比数值频散变化情况.为了定量分析空间差分数值频散，这里引入最佳入射角概念.当空间步长比和空间差分精度一定时，空间差分数值频散最小时对应的入射角即为最佳入射角.当l≠1时，在最佳入射角两侧，空间差分数值频散作用明显不同，入射角小于最佳入射角时空间差分数值频散影响较弱，相反超过最佳入射角时空间差分数值频散较严重，并且随着纵横网格步长比的增大，空间差分数值频散越发严重.而可变网格过渡带由于采用矩形网格离散，因此不可避免地会导致一定的数值频散现象产生，而通常过渡带处于非目标区域，因此一定的数值频散对目标区的精细数值模拟研究影响不大.同样也可以适当提高空间差分精度或者使入射角小于最佳入射角来压制空间差分数值频散的影响.

图 3

Fig. 3

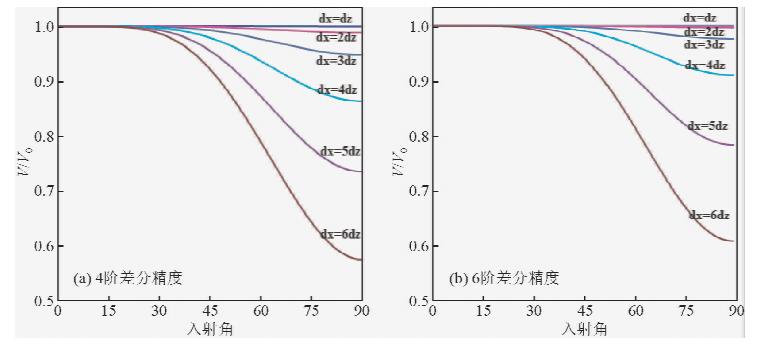图 3 不同纵横网格间距比数值频散曲线 Fig. 3 The numerical dispersion curve of the vertical and horizontal grid with different spacing ratio

为了验证可变交错网格算法的有效性和稳定性，在这里分别设计地堑和生物礁两个介质模型加以验证.

2.1 地堑介质模型

图 4为地堑介质模型，模型大小为1800 m×1800 m，速度从上至下依次为2000 m/s、2500 m/s、3000 m/s，介质的密度设为常数.可变交错网格数值模拟在模型虚线框内采用小尺度网格步长3 m×3 m，虚线框外采用大尺度网格步长为9 m×9 m；常规交错网格均采用小尺度网格步长3 m×3 m.

图 4

Fig. 4

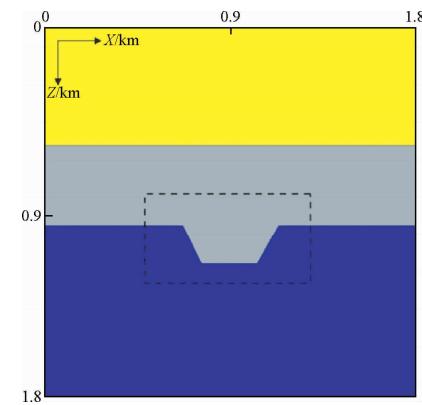图 4 地堑介质模型 Fig. 4 The graben medium model

在地表面激发，数值模拟精度为O(Δt²，Δx¹⁰).图 5、图 6分别为可变交错网格与常规交错网格数值模拟的波场快照和数值模拟记录.这里需要说明的是，由于大小尺度不同网格导致可变网格显示存在拉伸压缩现象，当波场从大尺度网格传播至小尺度网格，地震波场被压缩3倍，为了便于与常规交错网格模拟结果进行对比，只需对可变网格模拟结果进行一次重采样，即在小尺度网格采用9 m间距重新进行网格采样.

图 5

Fig. 5

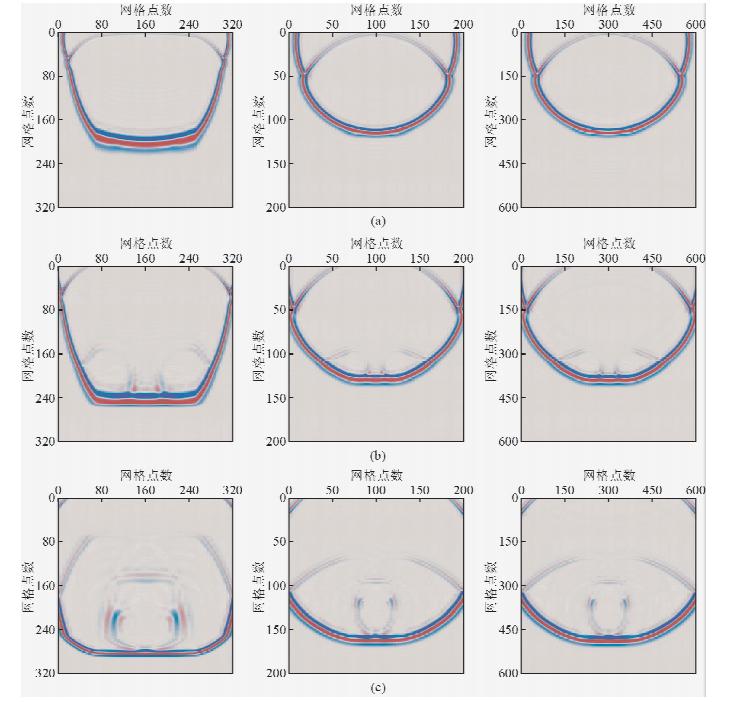图 5 可变交错网格与常规交错网格波场快照 (a)t=450 ms；(b)t=500 ms；(c)t=600 ms (左)可变交错网格；(中)处理后可变交错网格；(右)常规交错网格 Fig. 5 The wave field snapshot of variable staggered grid and conventional staggered grid

图 6

Fig. 6

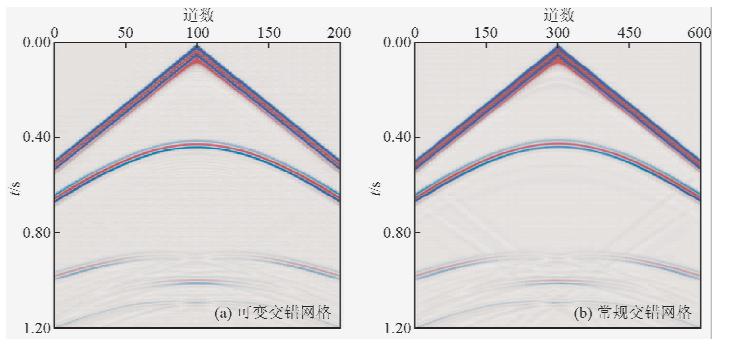图 6 可变交错网格与常规交错网格数值模拟记录 Fig. 6 The numerical simulation record of variable staggered grid and conventional staggered grid

从波场快照可以看出，当t=500 ms时，地堑两侧绕射点产生绕射波，在未处理可变交错网格波场快照中尤为明显，而处理后的可变交错网格与常规精细交错网格在地堑处精度基本一致，这是由于可变交错网格在地堑处采用小尺度网格离散的缘故.在数值模拟记录中，这里需要说明的是常规交错网格炮检距为3 m，可变交错网格炮检距为9 m.在地堑处两翼水平地层界面间断，使得两绕射波同相轴出现交叉现象，同时可变交错网格模拟记录和常规交错网格模拟记录具有较好的一致性.

2.2 生物礁介质模型

为了验证可变网格对复杂介质的适应性，这里设计了生物礁介质模型(如图 7所示).模型大小为2160 m×2160 m.可变网格在生物礁地质体附近即虚线框内采用小尺度网格3 m×3 m，在虚线框外采用大尺度网格9 m×9 m；常规细交错网格步长均为3 m×3 m，常规粗交错网格步长均为9 m×9 m，数值模拟精度均为 O(Δt²，Δx¹⁰).图 8为450 ms可变交错网格与常规细交错网格增益波场快照，图 9为生物礁介质模型可变交错网格与常规交错网格数值模拟记录.

图 7

Fig. 7

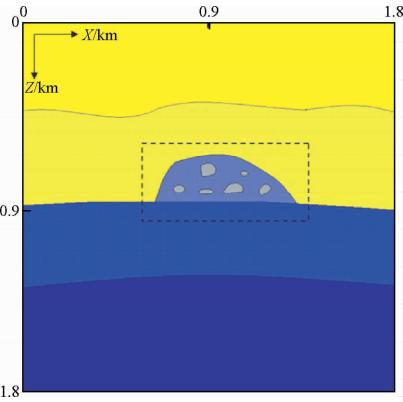图 7 生物礁介质模型 Fig. 7 The organic reefs medium model

图 8

Fig. 8

图 8 可变交错网格与常规细交错网格增益波场快照 Fig. 8 The gain wave field snapshot of variable staggered grid and conventional staggered grid

图 9

Fig. 9

图 9 生物礁可变交错网格与常规交错网格数值模拟记录 Fig. 9 The numerical simulation record of variable staggered grid and conventional staggered grid based on organic reefs

从生物礁介质增益波场快照中可以看出，可变网格与精细网格在波场精度刻画上基本一致，在箭头①所示处由于可变网格采用大尺度网格步长，因此出现轻微的数值频散现象，而对应在精细网格由于采用小尺度网格步长数值频散不明显；在箭头②生物礁处，由于可变网格采用小尺度网格步长其计算精度与精细网格步长基本一致.因此可变网格数值模拟在保证模拟效率的前提下更有利于对局部波场的精细刻画.

从数值模拟记录分析，对比图中虚线框部分模拟记录，可变网格由于在生物礁地质体处采用小尺度精细网格，达到了与常规精细网格精度一致的波场刻画.而对比常规粗网格模拟记录，可变网格只在箭头所示处有轻微的数值频散现象，这里常规粗网格在生物礁底部也出现了因空间差分而导致的数值频散现象.表 2给出了不同网格类型对生物礁介质数值模拟所用的计算时间，常规细交错网格模拟时间为常规粗交错网格模拟时间的11.93倍，计算效率明显降低；采用可变交错网格相对于常规细交错网格数值模拟计算效率提高了7.75倍.因此采用多尺度网格剖分的可变交错网格算法不仅提高了局部波场特征的分辨率，而且数值模拟的计算效率相对于常规细交错网格也有明显的提升，进一步增强了数值模拟对复杂介质的适应性.

表 2(Table 2)

表 2 不同网格类型对生物礁介质模型的计算时间 Table 2 The computation time of different grid type corresponding reefs medium model 网格类型 网格步长(m) 计算效率(s) 相对常规粗网格计算时间倍数 常规粗交错网格 9 m×9 m 186.844 1.00 可变交错网格 粗网格9 m×9 m 细网格3 m×3 m 288.188 1.54 常规细交错网格 3 m×3 m 2229.937 11.93

表 2 不同网格类型对生物礁介质模型的计算时间 Table 2 The computation time of different grid type corresponding reefs medium model

本文在常规交错网格高阶有限差分算法的基础上，进一步给出了可变网格高阶有限差分算法.尤其是以精细的岩性构造储层为研究对象，不得不考虑小尺度非均质性对地震波传播规律的影响，为此引入不同区域采用不同尺度网格离散的可变网格算法.从地堑介质模型和生物礁介质模型的模拟实例，主要获得以下几方面结论和认识：

(1)传统的可变网格算法一般采用插值方法解决大小尺度网格边界问题，一方面降低了数值模拟效率，另一方面插值必然会引入一定的计算误差积累，为了避免插值因素的影响，本文在大小尺度网格边界适当引入过渡区域，可以实现模型的自然、逐渐过渡，提高波场数值模拟的稳定性.

(2)可变网格算法在大小尺度网格边界未产生人工反射问题，从一定程度上说明算法的稳定性.同时一方面采用大尺度网格对构造简单的均匀介质即可满足对稳定性的保障和数值频散抑制的要求，另一方面小尺度网格能够达到对模型物性横向变化较大或者精细介质进行精细刻画，使模拟效率与模拟精度都能满足研究的要求.