2. 长安大学 地质工程与测绘学院, 西安 710054
2. School of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China
瞬变电磁法(TEM法)属于时间域电磁感应法,通过向地下发送一次脉冲场,在一次脉冲磁场间歇期间接收二次场,该二次场是由地下良导地质体受激励引起的涡流所产生,故可根据二次场衰减曲线特征判断地下地质体的电性、规模、产状等(李貅,2002).近年来瞬变电磁法一维、2.5维、三维正演都取得了较大的进展(岳建华等,2007;薛国强等,2008;丁艳飞等,2012;李建慧等,2012;孙怀凤等,2013);一些学者又提出了新的瞬变电磁数据处理方法(薛国强等, 2004,2013;李貅等, 2007,2010,2012),使得瞬变电磁法广泛应用于环境和工程领域(张保祥和刘春华,2004;嵇艳鞠等,2005;杨建军等,2006;韩自豪等,2008;薛国强和李貅,2008).目前国内用于煤田采空区勘探的地球物理方法主要有人工地震法、高密度电法、瞬变电磁法、地质雷达法等(唐庆兵等,2001).当煤田采空区位于潜水面以下时多富水,与围岩存在显著电阻率差异,使得电磁感应类方法成为最有效的勘探工具之一(杨建军等,2006).
大定源回线TEM法具有工作效率高,信号强度大,横向分辨率高等优点,用于采空区勘探的电磁类方法多以此方法为主(冯兵等,2010).该方法利用中心回线晚期视电阻率进行定性解释,为了提高工作效率,作业一般都在回线中心某一范围内测量.这样导致不满足晚期条件的早期道视电阻率计算结果偏大;当勘探区距离回线边较近时受场不均匀影响,存在“边界效应”.全区视电阻率可解决上述两个问题(冯兵等,2010).诸多学者对回线源TEM法垂直磁场分量定义的全区视电阻率进行计算:白登海等(2003)提出时间域瞬变电磁法中心方式全程视电阻率的数值计算方法;熊彬(2005)利用逆样条插值法计算大回线瞬变电磁法全区视电阻率;李建平等(2007)利用水平电偶极子合成回线源,再利用水平电偶极子垂直磁场求取任意形状回线全区视电阻率;王华军(2008)利用平移算法计算中心回线方式瞬变电磁全区视电阻率;张成范等(2009)利用二分搜索算法计算矩形大定源回线瞬变电磁测深全区视电阻率;武军杰等(2013)提出利用磁偶极子等效的大定源回线瞬变响应的视电阻率定义.
其中偶极子合成回线源方式可计算回线内任意点全区视电阻率(李建平等,2007;武军杰等2013);二分法计算全区视电阻率具有总是稳定收敛、不发散的特点(张成范等,2009). 但利用偶极子合成回线源方式和二分法计算时,每搜索一次,需要计算几十次误差函数,误差函数积分计算十分耗时.陈清礼(2009)研究了一种改进算法计算误差函数,计算一个测点仍需要1min左右,使得用该方法处理大量实测数据受到限制.本文用自变量复杂化的双曲正切函数近似误差函数,解决了全区视电阻率计算速度慢的问题,计算一个40道实测点耗时不到1s.作者编制了相关程序,对煤矿采空区勘探中实测回线源TEM数据进行全区视电阻率处理,得到较好结果.
1 算法 1.1 晚期视电阻率
圆型回线源瞬变晚期视电阻率可做如下定义(李貅,2002),均匀半空间上圆型回线中心点处垂直磁感应强度对时间变化率为

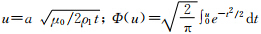 ,L1和L2分别为矩形回线的边长,μ0为磁率;
,L1和L2分别为矩形回线的边长,μ0为磁率; 为误差函数.
为误差函数.在晚期,u<<1,(1)可简化为


本文利用水平电偶极子合成回线源方式计算全区视电阻率(李建平等,2007).全区视电阻率有两重含义,首先不分早晚期,其次与回线内测量位置无关,不受回线内场不均匀影响,即不存在“边界效应”.
水平电偶极子均匀半空间上垂直磁感应强度对时间变化率为

 ,y为测点纵坐标.
,y为测点纵坐标.则均匀半空间上矩形回线源一条边激发的垂直磁感应强度对时间变化率可由水平电偶极子激发的垂直磁感应强度对时间变化率沿回线边积分得到

则均匀半空间上矩形回线源任意位置垂直磁感应强度对时间变化率为
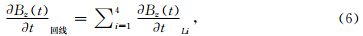
1.3 误差函数的处理
对Φ(u)稍作变换便可得到误差函数一般表达式

前言已提到,误差函数直接积分计算十分耗时.为了提高计算效率,我们用双曲正切函数近似计算法来计算误差函数值(田锦州等,2009),并与Matlab软件erf函数计算结果(这里认为是误差函数真实值的最佳近似值)进行对比来验证该方法的有效性.
从图 1a可看出,直接用双曲正切函数来近似误差函数,当u<1时,相对误差达到12%.为此,对双曲正切函数tanh(x)的自变量复杂化,表示为tanh[f(x)],假设双曲正切函数自变量为f(x)时,与自变量为x的误差函数相等,即
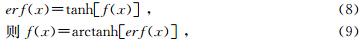
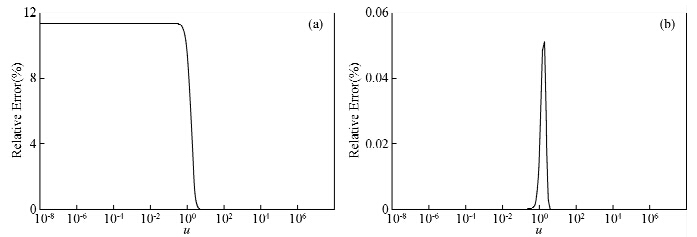 |
图 1 利用双曲正切函数来近似误差函数的相对误差 (a)用tanh(x)近似;(b)用tanh[f(x)]近似. Fig. 1 Relative error of using tanh function to approximate erf function (a)Using tanh(x) to approximate;(b)Using tanh[f(x)] to approximate. |
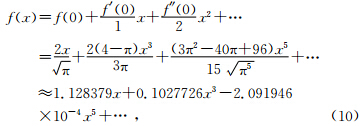
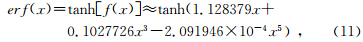
至此,用自变量复杂化的双曲正切函数近似误差函数,避免了直接数值积分的耗时,使得计算全区视电阻率的效率有了很大提高.作者编制了相关处理程序,计算一个40道测点仅需不到1 s时间.
2 算法验证
前面介绍了全区视电阻率计算方法.下面利用一维理论模型正演结果计算全区视电阻率,来验证该方法的有效性和利用双曲正切函数近似误差函数的正确性.表 1为一维理论模型参数表;图 2为发射回线与测点位置示意图.回线边长为400×400 m;点距为20 m;供电电流为10 A;测道数为40道;采样窗口时间为0.087~712.7 ms.
|
|
表 1 一维理论模型参数表 Table 1 Parameters for 1D forward model |
 | 图 2 正演发射回线与测点示意图 Fig. 2 Schematic of transmitter loop and measuring measuring polnt polisttion for forward |
图 3为回线中心点调用Matlab误差函数和自变量复杂化的双曲正切函数代替误差函数计算全区视电阻率的曲线对比图,从(a)可看出,两曲线基本重合,从图(b)可看出,双曲正切函数在早期道计算误差较大,但小于0.2%,因此可利用自变量复杂化的双曲正切函数代替误差函数计算全区视电阻率.
 |
图 3 中心点两种误差函数计算方法全区视电阻率对比 (a)全区视电阻率;(b)相对误差. Fig. 3 All-time apparent resistivity comparison using two erf function calculation method at middle point (a)All-time apparent resistivity;(b)Relative error. |
图 4为连续三个回线框内视电阻率多测道断面图,(b)晚期视电阻率断面图存在很强“边界效应”,横向形成向下弯曲的圆弧等值线,中部低阻、边部高阻,此外,在第20道附近每个框内都形成一个圈闭假异常,这是由于晚期视电阻率“边界效应”影响范围大,以至在较深部(20道附近)依然等值线呈向下弯曲的圆弧状,形成了第20道附近假异常;(a)全区视电阻率断面图在对应视电阻率曲线假极值点附近出现不平直,但不存在晚期视电阻率“边界效应”.全区视电阻率在早期道不存在晚期视电阻率假高值,更能反映地电断面特征.
 |
图 4 理论模型H型不同视电阻率多测道断面图 (a)全区视电阻率;(b)晚期视电阻率. Fig. 4 Profile of H-type apparent resistivity (a)All-time apparent resistivity;(b)Later-time apparent resistivity. |
3.1 工区地质概况及地球物理特征
勘探区域位于山西宁武煤田南端,井田内总体为单斜构造,且全部被新生界地层覆盖,根据钻孔揭露及勘探区资料,地层自老到新有:奥陶系中统峰峰组(O2f),岩性以厚层状致密石灰岩为主,电性表现为高阻;石炭系中统本溪组(C2b),以砂岩、砂质泥岩、泥岩为主,电性表现为中高阻;上统太原组(C3t),为主要含煤地层,以砂质泥岩、泥岩、煤层为主,电性表现为中低阻;二叠系下统山西组(P1s),主要为泥岩、砂质泥岩、煤层,下石盒子组(P1x)、上统上石盒子组(P2s)均以泥岩、砂质泥岩为主,电性表现为中低阻;上新近系上新统(N2),以粘土、亚粘土为主,电性表现为低阻;第四系(Q),主要为含砂粘土、亚砂土、上覆现代冲洪积物,电性表现为中低阻,大约100 Ω · m左右,且存在局部不均匀体.含煤地层主要为太原组(C3t)和山西组(P1s),约150 m厚,可采煤层均位于山西组(P1s)内,深度为250 m到330 m;峰峰组(O2f)为煤系地层基底.本次勘探任务要求基本查明勘探区山西组内煤层空区及采空积水区的范围及状况.
3.2 瞬变电磁数据采集
本次勘探使用长沙白云仪器开发公司生产的MSD-1脉冲瞬变电磁仪.经过实地实验之后,确定如下工作参数:大回线框边长为400 m;频率为75 Hz;采样窗口时间为0.024~2.88毫秒;测道数为40道;发射电流为7A左右;叠加次数为512次;延时为250微秒;接收探头等效面积为2000 m2.图 5为实际测量回线与测点位置示意图,十字点为实测点.
 | 图 5 实测发射回线与测点位置示意图 Fig. 5 Schematic of transmitter loop and measuring point position for measurement |
数据处理采用全区视电阻率方法,并与晚期视电阻率计算结果做对比.这里选228线处理结果.图 6为228线150点和170点全区视电阻率和晚期视电阻率曲线对比图,可以看出全区视电阻率曲线和晚期视电阻率曲线在早期道有差异,在晚期道基本重合.浅部地层主要为第四系的含砂粘土、亚砂土,电阻率相对较低,一般为100 Ω · m左右.晚期视电阻率由于在早期不满足晚期条件,计算结果偏大,与实际不符;全区视电阻率计算结果与实际地层电阻率较接近.在图 6a中全区视电阻率对浅部的相对低阻异常有很好的反映,而晚期视电阻率表现为相对高阻.
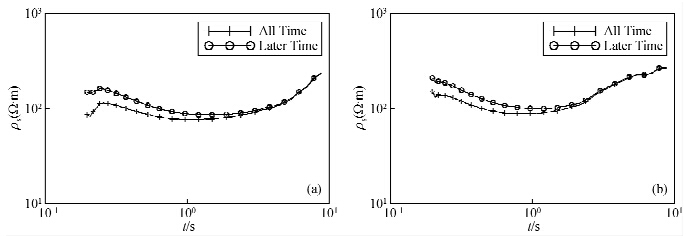 |
图 6 228线全区视电阻率和晚期视电阻率曲线对比 (a)150号点;(b)170号点.All Time:全区视电阻率曲线;Later Time:晚期视电阻率曲线 Fig. 6 Comparison between all-time and later-time apparent resistivity curve about line 228 (a)Point of 150;(b)Point of 170. |
图 7为228线两种不同方式处理得到的视电阻率断面图:(a)为全区视电阻率断面图,(b)为晚期视电阻率断面图.228线与回线框位置关系在图 5中给出.可看出两幅图在浅部差异比较大,深部基本无差别.在海拔1200~1250 m之间,晚期视电阻率断面图表现为高阻,均在130 Ω · m以上,最高可达280 Ω · m,大于地层真实电阻率;全区视电阻率断面图表现为低阻,在100 Ω · m左右,存在相对高阻和相对低阻的局部异常,反映了第四系地层和存在的局部不均匀体,与地层的真实情况最为符合.在海拔1000~1200 m之间,视电阻率断面图均表现出低阻异常,反映了上新近系上新统的粘土和亚粘土层;在海拔800~1000 m之间,视电阻率表现为中低阻和下凹的局部低阻异常,推测该层为含煤的太原组和山西组泥沙岩地层,下凹的局部低阻异常是采空区引起,此类异常与已知采空区对应较好,据此推断两个可能采空区.在海拔800 m以下,视电阻率表现为高阻,反映了奥陶系峰峰组致密石灰岩.
 |
图 7 228线全区视电阻率和晚期视电阻率断面图对比 (a)全区视电阻率断面图;(b)晚期视电阻率断面图. Fig. 7 Comparison between all-time and later-time apparent resistivity section about line 228 (a)Section of all-time apparent resistivity;(b)Section of later-time apparent resistivity. |
周楠楠等(2011)研究发现在观测晚期,回线内垂直磁场分布较均匀,早期响应分布具有中间大,周边小的特点.因此在利用晚期视电阻率公式计算时,在早期存在“边界效应”,该效应在视电阻率等值线断面图表现为横向上形成向下弯曲的圆弧等值线,中部低阻、边部高阻(冯兵等,2010).在228线晚期视电阻率断面图上同样存在该效应,表现为一个框在早期形成一个圈闭的假异常,给解释带来误导.但在228线全区视电阻率断面图上,该效应基本消除,方便解释.
在图 7a中,在浅层147~153点之间,存在局部相对低阻异常,该异常在图 7b中基本无显示.是因为晚期视电阻率在早期道存在假高值,掩盖了浅层低阻异常;全区视电阻率对浅层相对低阻异常有明显、直观地反映,更加符合客观规律.当煤层埋深较浅,有过小规模个人开采,在浅层可能存在积水小煤窑,表现为局部低阻.若浅层积水小煤窑不在勘探盲区,则全区视电阻率对其有很好反映,晚期视电阻率则受早期道假高值影响对其反映不明显.因此全区视电阻率对探测埋深较浅的积水小煤窑具有重要意义.
4 结 论4.1利用偶极子合成回线方式和二分法可计算矩形回线源内任意位置全区视电阻率,但需计算多次误差函数,直接利用数值积分计算该函数十分耗时.为此,本文利用自变量复杂化的双曲正切函数近似误差函数,提高了计算效率,可以很快计算出实测数据全区视电阻率.
4.2一维理论模型计算结果表明:利用自变量复杂化的双曲正切函数代替误差函数计算得到的全区视电阻率误差较小;全区视电阻率不存在晚期视电阻率“边界效应”,在早期道不存在晚期视电阻率假高值,更能反映地电断面特征.
4.3在矩形大定源回线TEM煤田采空区勘探中,全区视电阻率基本消除了中心回线晚期视电阻率存在的“边界效应”,有利于解释;全区视电阻率不存在晚期视电阻率在早期道的假高值,接近地表真实电阻率,对近地表局部异常有较好反映,对探测埋深较浅的积水小煤窑具有重要意义.
致 谢 感谢评审老师和编辑对本文的帮助.| [1] | Bai D H, Meju M A, Lu J, et al. 2003. Numerical calculation of all-time apparent resistivity for the central loop transient electromagnetic method[J]. Chinese J. Geophys. (in Chinese), 46(5): 697-704. |
| [2] | Chen Q L. 2009. Searching algorithm for full time apparent resistivity from tem electromotive force data[J]. Journal of Oil and Gas Technology (J. JPI) (in Chinese), 31(2): 45-49. |
| [3] | Ding Y F, Bai D H, Xu C. 2012. A rapid algorithm for calculating time domain transient electromagnetic responses of a large fixed rectangular loop on the half space[J]. Chinese J. Geophys. (in Chinese), 55(6): 2087-2096, doi: 10.6038/j.issn.0001-5733.2012.06.030. |
| [4] | Feng B, Meng X H, Zhang B. 2010. Transmitting coil boundary effect for TEM large loop source and elimination method[J]. Coal Geology & Exploration (in Chinese), 38(5): 61-66. |
| [5] | Han Z H, Wei W B, Zhang W B. 2008. Study on the exploration depth of transient electromagnetic method in northern China coalfield[J]. Progress in Geophysics (in Chinese), 23(1): 237-241. |
| [6] | Ji Y J, Lin J, Zhu K G, et al. 2005. Underground water prospecting by Transient electromagnetic method[J]. Progress in Geophysics (in Chinese), 20(3): 828-833. |
| [7] | Li J H, Zhu Z Q, Zeng S H, et al. 2012. Progress of forward computation in transient electromagnetic method[J]. Progress in Geophysics (in Chinese), 27(4): 1393-1400, doi: 10.6038/j.issn.1004-2903.2012.04.013. |
| [8] | Li J P, Li T L, Zhao X F, et al. 2007. Study on the TEM all-time apparent resistivity of arbitrary shape loop source over the layered medium[J]. Progress in Geophysics (in Chinese), 22(6): 1777-1780. |
| [9] | Li X. 2002. Theory and Application of Transient Electromagnetic Sounding[M]. Xi'an: Shanxi Science Press. |
| [10] | Li X, Xue G Q, Guo W B. 2007. Research progress in TEM pseudo-seismic imaging[J]. Progress in Geophysics (in Chinese), 22(3): 811-816. |
| [11] | Li X, Qi Z P, Xue G Q. 2010. Three dimensional curved surface continuation image based on TEM pseudo wave-field[J]. Chinese J. Geophys. (in Chinese), 53(12), 3005-3011, doi: 10.3969/j.issn.0001-5733.2010.12.025. |
| [12] | Li X, Xue G Q, Liu Y A, et al. 2012. A research on TEM imaging method based on synthetic-aperture technology[J]. Chinese J. Geophys. (in Chinese), 55(1): 333-340, doi: 10.6038/j.issn.0001-5733.2012.01.034. |
| [13] | Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese J. Geophys. (in Chinese), 56(3): 1049-1061, doi: 10.6038/cjg20130333. |
| [14] | Tang Q B, Li D X, Fan W Y. 2001. Synthetic method of georadar and one meter geothermomery for the determination of the mined region and area on fire in a coal field[J]. Geological Science and Technology Information (in Chinese), 20(3): 95-100. |
| [15] | Tian J Z, Xu L Z, Li F M. 2009. Proximate calculation of error function erf(x) and its application in mining subsidence prediction[J]. Coal Mining Technology (in Chinese), 14(2): 33-35. |
| [16] | Wang H J. 2008. Time domain transient electromagnetism all time apparent resistivity translation algorithm[J]. Chinese J. Geophys. (in Chinese), 51(6): 1936-1942. |
| [17] | Wu J J, Zhang J, Wang C X, et al. 2013. Calculation of fixed TEM response and apparent resistivity based on equivalent magnetic dipole[J]. Coal Geology & Exploration (in Chinese), 4(3): 68-71. |
| [18] | Xiong B. 2005. Inverse spline interpolation for the calculation of Al-l Time resistivity for the large-loop transient electromagnetic method[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 35(4): 515-519. |
| [19] | Xue G Q, Li X, Song J P, et al. 2004. Theoretical analysis and numerical calculation of loop-source transient electromagnetic imaging[J]. Chinese J. Geophys. (in Chinese), 47(2): 338-343. |
| [20] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
| [21] | Xue G Q, Li X. 2008. The technology of TEM tunnel prediction imaging[J]. Chinese J. Geophys. (in Chinese), 51(3): 894-900. |
| [22] | Xue G Q, Chen W Y, Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding[J]. Chinese J. Geophys. (in Chinese), 56(1): 255-261, doi: 10.6038/cjg20130126. |
| [23] | Yue J H, Yang H Y, Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine[J]. Progress in Geophysics (in Chinese), 22(6): 1904-1909. |
| [24] | Yang J J, Wu H N, Feng B, et al. 2006. Research on prospecting effect for gob area of coal mines[J]. Coal Geology & Exploration (in Chinese), 34(1): 67-70. |
| [25] | Zhang B X, Liu C H. 2004. Summarization on applications to groundwater exploration by using transient electromagnetic methods[J]. Progress in Geophysics (in Chinese), 19(3): 537-542. |
| [26] | Zhang C F, Weng A H, Sun S D, et al. 2009. Computation of whole-time apparent reisistivity of large rectangular loop[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 39(4): 755-758. |
| [27] | Zhou N N, Xue G Q, Li M F, 2011. et al. Response of large-loop TEM based on approximation of electric dipole[J]. Coal Geology & Exploration (in Chinese), 39(4): 50-54. |
| [28] | 白登海, Meju M A, 卢健,等. 2003. 时间域瞬变电磁法中心方式全程视电阻率的数值计算[J]. 地球物理学报, 46(5): 697-704. |
| [29] | 陈清礼. 2009. 瞬变电磁法全区视电阻率的二分搜索算法[J]. 石油天然气学报(江汉石油学院学报), 31(2): 45-49. |
| [30] | 丁艳飞, 白登海, 许诚. 2012. 均匀半空间表面大定源瞬变电磁响应的快速算法[J]. 地球物理学报, 55(6): 2087-2096, doi: 10.6038/j.issn.0001-5733.2012.06.030. |
| [31] | 冯兵, 孟小红, 张斌. 2010. TEM框内回线装置发射框边界影响及消除方法[J]. 煤田地质与勘探, 38(5): 61-66. |
| [32] | 韩自豪, 魏文博, 张文波. 2008. 华北煤田瞬变电磁勘探深度研究[J]. 地球物理学进展, 23(1): 237-241. |
| [33] | 嵇艳鞠, 林君, 朱凯光,等. 2005. 利用瞬变电磁技术进行地下水资源勘察[J]. 地球物理学进展, 20(3): 828-833. |
| [34] | 李建慧, 朱自强, 曾思红,等. 2012. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 27(4): 1393-1400, doi: 10.6038/j.issn.1004-2903.2012.04.013. |
| [35] | 李建平, 李桐林, 赵雪峰,等. 2007. 层状介质任意形状回线源瞬变电磁全区视电阻率的研究[J]. 地球物理学进展, 22(6): 1777 -1780. |
| [36] | 李貅. 2002. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社. |
| [37] | 李貅, 薛国强, 郭文波. 2007. 瞬变电磁法拟地震成像研究进展[J]. 地球物理学进展, 22(3): 811-816. |
| [38] | 李貅, 戚志鹏, 薛国强. 2010. 瞬变电磁虚拟波场的三维曲面延拓成像[J]. 地球物理学报, 53(12), 3005-3011, doi: 10.3969/j.issn.0001-5733.2010.12.025. |
| [39] | 李貅, 薛国强, 刘银爱,等. 2012. 瞬变电磁合成孔径成像方法研究[J]. 地球物理学报, 55(1): 333-340, doi: 10.6038/j.issn.0001-5733.2012.01.034. |
| [40] | 孙怀凤, 李貅, 李术才,等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演[J]. 地球物理学报, 56(3): 1049-1061, doi: 10.6038/cjg20130333. |
| [41] | 唐庆兵, 李大心, 樊武义. 2001. 综合物探方法在煤田采空区圈定和着火区调查中的应用研究[J]. 地质科技情报, 20(3): 95-100. |
| [42] | 田锦州, 徐乃忠, 李凤明. 2009. 误差函数erf(x)近似计算及其在开采沉陷预计中的应用[J]. 煤矿开采, 14(2): 33-35. |
| [43] | 王华军. 2008. 时间域瞬变电磁法全区视电阻率的平移算法[J]. 地球物理学报, 51(6): 1936-1942. |
| [44] | 武军杰, 张杰, 王兴春,等. 2013. 基于等效磁偶极子的定源回线瞬变响应计算方法及视电阻率定义[J]. 煤田地质与勘探, 4(3): 68-71. |
| [45] | 熊彬. 2005. 大回线瞬变电磁法全区视电阻率的逆样条插值计算[J]. 吉林大学学报(地球科学版), 35(4): 515-519. |
| [46] | 薛国强, 李貅, 宋建平,等. 2004. 回线源瞬变电磁成像的理论分析及数值计算[J]. 地球物理学报, 47(2): 338-343. |
| [47] | 薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 23(4): 1165-1172. |
| [48] | 薛国强, 李貅. 2008. 瞬变电磁隧道超前预报成像技术[J]. 地球物理学报, 51(3): 894-900. |
| [49] | 薛国强, 陈卫营, 周楠楠,等. 2013. 接地源瞬变电磁短偏移深部探测技术[J]. 地球物理学报, 56(1): 255-261, doi: 10.6038/cjg20130126. |
| [50] | 岳建华, 杨海燕, 胡搏. 2007. 矿井瞬变电磁法三维时域有限差分数值模拟[J]. 地球物理学进展, 22(6): 1904-1909. |
| [51] | 杨建军, 吴汉宁, 冯兵,等. 2006. 煤矿采空区探测效果研究[J]. 煤田地质与勘探, 34(1): 67-70. |
| [52] | 张保祥, 刘春华. 2004. 瞬变电磁法在地下水勘查中的应用综述[J]. 地球物理学进展, 19(3): 537-542. |
| [53] | 张成范, 翁爱华, 孙世栋,等. 2009. 计算矩形大定源回线瞬变电磁测深全区视电阻率[J]. 吉林大学学报(地球科学版), 39(4): 755-758. |
| [54] | 周楠楠, 薛国强, 李梅芳,等. 2011. 基于电偶极子近似的多边形回线源瞬变电磁响应[J]. 煤田地质与勘探, 39(4): 50-54. |
 2015, Vol. 30
2015, Vol. 30

