2. 中煤科工集团西安研究院有限公司, 西安 710077;
3. 中石油长庆油田勘探开发研究院, 西安 710049
2. China Coal Research Institute Xi'an Science and Industry Group, Xi'an 710077, China;
3. Research Institute of Exploration and Development, Petro Changqing Oilfield Company, Xi'an 710077, China
0 引 言
由于流体渗流过程的复杂性,相对渗透率受到岩石润湿性、流体间界面张力、储层孔隙结构、温度、流体粘度等多种因素影响,而试验所测得的相渗曲线正是各种影响因素综合的结果(黄祥峰等,2013).因此,相对渗透率曲线在油气田开发中得到广泛应用,比如计算开发指标,进行动态分析,确定储层中流体分布,计算驱气效率和预测采收率(孟召平等,2010)等.目前,气水两相相对渗透率曲线主要通过取心岩样在室内实验室测定.气藏开发过程中采集的是多层合采的生产数据,其渗流特征包含储层非均质性以及不同样品润湿性差异,需要用一条相渗曲线反映气藏总的渗流特征.拟合油气藏综合相渗曲线在实践中已广泛应用,但对致密砂岩气藏相渗曲线的拟合却鲜有研究.国内外现有的拟合方法都是用较早的经验公式进行拟合(戴胜群等,2011),拟合误差较大且并不完全适用于致密砂岩气藏.本文利用实验室气水相渗数据,通过孔隙度和渗透率对数与自由气饱和度的关系筛选出合格的相渗曲线并根据气、水相对渗透率曲线的交点(即等渗点)及曲线形态把相渗曲线分为了三类.然后利用自动历史拟合方法推导出了综合相渗曲线的定量表达式,实现了对气水相渗曲线的归一化,平均拟合相对误差在18%以下.
1 气水相渗曲线的筛选与分类
由于受岩样完好程度、仪器灵敏度、试验条件和读数误差等因素影响,不是所有岩心得到的相渗曲线都符合一般的渗流规律.因此对相渗曲线进行筛选,优选出试验误差小、试验结果合理的相渗曲线作为区块拟合相渗曲线的基础曲线进而对相渗曲线进行统一描述是十分必要的.岩心样品在一定试验压差下,大的孔喉孔隙能够参与流动,小的孔喉孔隙因渗流阻力大不能参与流动.即随颗粒粒径增加,可参与流动的孔隙体积增加,自由气饱和度随渗透率增加而升高.根据统计结果,孔隙度和渗透率对数与自由气饱和度呈直线关系.


致密砂岩储集层孔隙连通性差异大,孔隙结构比较复杂,属于非均质性较强的储集层.岩石的润湿性、饱和顺序、岩石孔隙结构、温度、流体粘度、毛管力等因素都将增加相渗曲线形态的复杂性,无法直接对所有相渗曲线进行非线性拟合.因此可以根据反映上述因素影响结果的等渗点将相渗曲线分为三类.图 1是基于长庆油田苏东的气水相渗试验数据得到的气水相渗曲线分类图.由图 1可以看出,第1类的气水相渗曲线的交点在水饱和度Sw=64%左右,第2类的气水相渗曲线的交点在Sw=68%左右,第3类的气水相渗曲线的交点在Sw=73%左右.
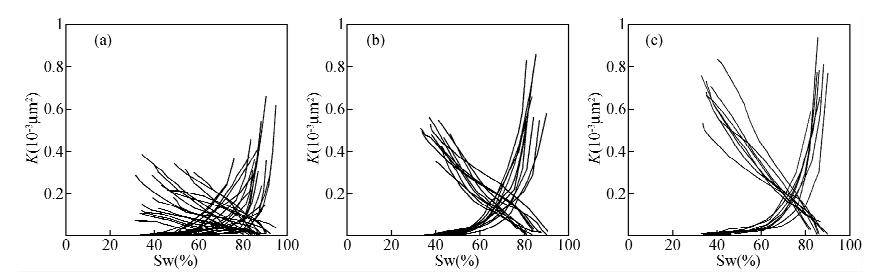 |
图 1 气水相渗曲线分类 (a)第1类气水相渗曲线;(b)第2类气水相渗曲线;(c)第3类气水相渗曲线. Fig. 1 Gas-water relative permeability curve classification (a)First type of gas-water relative permeability curve;(b)Second type of gas-water relative permeability curve; (c)Third type of gas-water relative permeability curve. |
图 2是根据图 1中每一类气水相渗曲线的曲线形态及两相渗流区的范围,将横坐标Sw等分,求取每一个小区域内Sw和Krw或Krg的平均值作为本区域的一个数据点从而产生的每一类气水相渗曲线的代表曲线.Krw,Krg分别为水和气的相对渗透率.
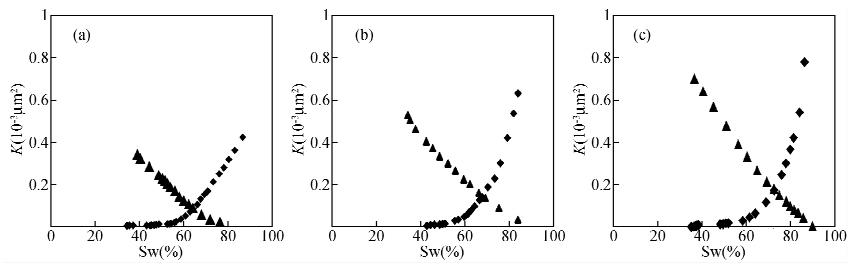 |
图 2 各类相渗曲线的代表曲线 (a)第1类代表曲线;(b)第2类代表曲线;(c)第3类代表曲线. Fig. 2 Representative curves of various phase permeability curve (a)First type of representative curve;(b)Second type of representative curve; (c)Third type of representative curve. |
试验得到的相渗曲线为离散的数值,自上世纪50年代起,不少学者研究了利用试验数据回归经验公式表征相渗曲线,找到了一些经验公式.比如Jone Park J等(1945)对于砂岩和泥质砂岩提出的关系式,柯里(Corey,1954)公式、霍纳普(Honarpour,1982)公式和勒克(Lake,1985)公式等.
|
|
表 1 求取相对渗透率的经验公式 Table 1 Empirical formulas of calculating relative permeability |
用上述经验公式对长庆致密砂岩气藏气水相渗曲线进行拟合发现拟合相对误差都在26%以上,有的甚至达到35%以上,拟合参数无法实现归一化.主要原因为上述经验公式都是针对油藏或油气藏,而岩石对油、气润湿性存在差异并且流体的粘度不同,缺少对气藏特点的专一性研究,因此降低了拟合效果.本文根据最基本的Jone Park J等(1945)对于砂岩和泥质砂岩提出的油水两相经验公式并结合相渗曲线的物理意义,去掉油的影响而加入残余气的影响因子及分析水、气、油三相的关系,得到如下关系式:
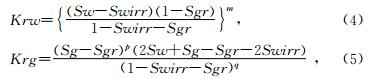
3 气水相渗曲线的归一化处理
不同样品的气水相渗曲线,其束缚水饱和度和残余气饱和度不等,而且试验曲线记录的数据个数和相对渗透率对应的含水饱和度均不相等,因此单一类的样品曲线不能直接代表综合相渗曲线,需要进行归一化处理.归一化后的综合相渗曲线使得气水相渗公式中的拟合参数唯一且可以较好地满足于每一类相渗曲线.
归一化处理的具体步骤为:
(1)将每一类气水相渗代表曲线与相渗定量公式计算曲线分别拟合,得到各自拟合误差最小时的m、p、q值;
(2)根据每一类相渗曲线确定的m、p、q值明确拟合参数的范围;
(3)综合拟合所有代表曲线的气水相渗数据,在m、p、q范围里,综合考虑绝对误差和相对误差的大小,确定最终的拟合参数.
根据以上步骤,以长庆油田东二区气水相渗数据为例,得到的气水相渗公式为
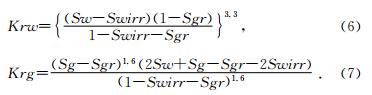
图 3为每一类试验相渗曲线及其公式拟合的曲线.从图中可以看出,归一化后的相渗公式可以较好地代表综合相渗曲线.表 2是对每一类相渗曲线拟合误差的统计.
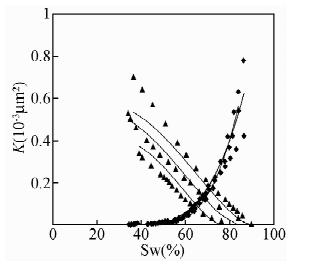 | 图 3 归一化气水相渗曲线 Fig. 3 Normalized gas-water relative permeability curve |
|
|
表 2 气水相渗拟合误差统计 Table 2 Gas-water relative permeability fitting error statistics |
选取图 1中每一类气、水相渗曲线各三条,用公式(6)、(7)进行拟合.相渗曲线的选取原则为每一类中选取的相渗曲线形态和数据值差异尽量大,这样可以较全面地说明气水相渗公式的可行性和准确性.图 4为各类选取的试验数据点和相渗公式拟合曲线图.
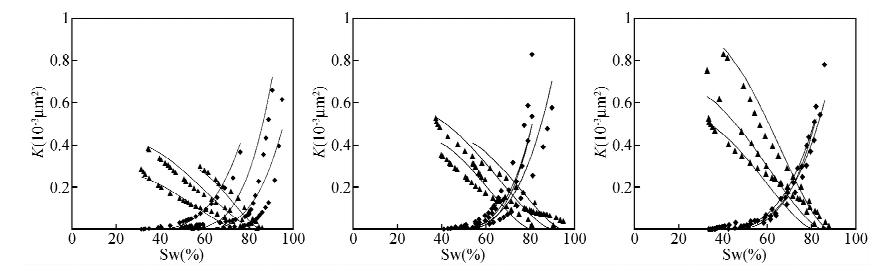 |
图 4 气水相渗试验数据点和其拟合曲线 (a)第1类试验数据点和拟合曲线;(b)第2类试验数据点和拟合曲线;(c)第3类试验数据点和拟合曲线. Fig. 4 Gas-water relative permeability test data points and the fitted curve (a)First type of test data points and the fitted curve;(b)Second type of test data points and the fitted curve; (c)Third type of test data points and the fitted curve. |
4.1 数据拟合前通过孔隙度和渗透率对数与自由气饱和度的关系筛选出合格的气水相渗曲线,有助于提高拟合的准确性;
4.2 对气水相渗曲线进行分类可以较全面地概括各类相渗情况;
4.3 用气水相渗代表曲线拟合气藏综合相渗曲线中的拟合参数关系到综合曲线是否能正确表征气藏渗流状况,是拟合气藏综合相渗曲线的关键步骤;
4.4 根据Jone Park J等(1945)的油水两相经验公式并结合相渗曲线的物理意义,去掉油的影响而加入残余气的影响因子及分析水、气、油三相的关系所建立的气水相渗公式拟合效果较好,对致密砂岩气藏采收率和流量比的预测具有指导性意义.
致 谢 感谢国家自然基金鄂尔多斯盆地大型低渗透岩性地层油气藏开发示范工程(2011ZX05044)和煤与煤层气地质条件精细探测技术与装备(2011ZX05040-002)的资助;感谢在项目研究期间给予帮助的各位专家老师以及地球物理学进展编辑部的支持与帮助!| [1] | Dai S Q, Fu B, Hong X E, et al.2011. The methods to fit the curve of integrated relative permeability in reservoir[J]. Reservoir Evaluation and Development,1(3):1-4. |
| [2] | Huang X F, Zhang G M, Guo J L, et al. 2013. New measurement methods for relative permeability cure and its application[J]. Petroleum Geology and Engineering,27(1):53-55. |
| [3] | Jia X F.2013.The Automatic History Matching Method to Calculate Relative permeability[D][Master's Thesis]. Beijing: China University of Geosciences. |
| [4] | Li M, Xiao W L, Guo X, et al. 2009.Laboratory study of the effective pressure law for permeability in Ta-Ba-Miao low-permeability sandstones[J]. Geophysics(in Chinese),52(12): 3166-3174. |
| [5] | Liu Z H, Wu S Q, Du B H, et al. 2013.Experimental study on the relationship between reservoir permeability and its formation resistivity factor[J]. Geophysics(in Chinese),56(6): 2088-2097. |
| [6] | Meng Z P, Hou Q L. 2013.Coupling model of stress-dependent permeability in high-rank coal reservoir and its control mechanism[J]. Geophysics(in Chinese),56(2): 667-675. |
| [7] | Sun D S, Li A W, Wang H C, et al. 2012. Experiment on anisotropy of permeability with tight sandstone[J]. Progress in Geophysics(in Chinese),27(3): 1101-1106. |
| [8] | Wang S G, Zhao G Z,Yu B J. 2005.Statistical regularity of oil-water relative permeability in Daqing Oilfield[J]. Acta Petrolei Sinica,26(3):78-81. |
| [9] | Zhang J C, Song K P.2007. Eigen Curve of relative permeability and its application[J]. Acta Petrolei Sinica,28(4):104-107. |
| [10] | 戴胜群,付波,洪秀娥,等.2011.油藏综合相渗曲线拟合方法[J].油气藏评价与开发,1(3):1-4. |
| [11] | 黄祥峰,张光明,郭俊磊,等.2013.计算油藏相渗曲线的新方法及应用[J].石油地质与工程,27(1):53-55. |
| [12] | 贾秀芬.2013.计算相对渗透率的自动历史拟合方法[D][硕士论文].北京:中国地质大学. |
| [13] | 李闽,肖文联,郭肖,等.2009.塔巴庙低渗致密砂岩渗透率有效应力定律实验研究[J].地球物理学报,52(12):3166-3174. |
| [14] | 刘忠华,吴淑琴,杜宝会,等.2013.储层渗透性与地层因素关系的实验研究与分析[J].地球物理学报,56(6):2088-2097. |
| [15] | 孟召平,侯泉林.2013.高煤级煤储层渗透性与应力耦合模型及控制机理[J].地球物理学报,56(2): 667-675. |
| [16] | 孙东生,李阿伟,王红才,等.2012.低渗砂岩储层渗透率各向异性规律的实验研究[J].地球物理学进展,27(3):1101-1106. |
| [17] | 王曙光,赵国忠,余碧君.2005.大庆油田油水相对渗透率统计规律及其应用[J].石油学报,26(3):78-81. |
| [18] | 张继成,宋考平.2007.相对渗透率特征曲线及其应用[J].石油学报,28(4):104-107. |
 2015, Vol. 30
2015, Vol. 30



