2. 油气藏地质及开发国家重点实验室, 成都 610500;
3. 中国科学院水库水环境重点实验室, 重庆 400714
2. State Key Laboratory of Gas Reservoir Geology and Exploitation, Chengdu 610500, China;
3. Key Laboratory of Reservoir Aquatic Environment, Chinese Academy of Sciences, Chongqing 400714, China
孔隙度是油气工业储量评价与产能预测的重要基础参数.在工程上主要利用声波、中子、密度测井曲线结合室内岩心实验建立储层孔隙度剖面,其中声波数据是最常用的矿场资料,声波的传播具有路径选择性,对于孔隙空间非均质性极强,离散孔洞发育的碳酸盐岩储层而言是否还能利用基于声波时差资料的Wyllie时间平均公式计算孔隙度有待研究.
目前,国内大部分研究集中在对于三曲线测井资料的矫正应用和利用数学手段对数据进一步精细处理(景建恩等,2003;漆立新等,2010;陈继华等,2011;赵辉等,2012).近些年出现了一些新的研究手段和数据处理方法,利用全直径岩心和小岩柱岩心间孔隙度的关系以实现测井孔隙度的正确预测(张豆娟等,2007;李淑荣等,2010).利用测井资料和最小二乘法拟合孔隙度与波阻抗的关系,建立预测模型(雷芬丽等,2010).研究不同压实情况下孔隙度对地震属性的影响,深度压实储层,反射系数随孔隙度的增加而减小;欠压实储层,反射系数随孔隙度的增加而增加(武国宁等,2013).利用电阻率数据通过递归分析受流体影响较小的测井资料建立了有效孔隙度计算模型(将进勇,2004).通过深入研究电成像测量方法,提出看一种基于电成像低频分量的电阻率刻度公式,结合阿尔奇公式,推导了基于电成像数据的孔隙度计算方法(李晓辉等,2012).
除了上述工程性应用研究,也有学者开展了大量基础理论与方法研究.利用人工物理模型下的超声波测试,分析了缝、洞孔隙度对地震波属性的影响,研究表明,随孔隙度增加,波速、振幅、衰减和主频等都有不同程度的减小,并且振幅、衰减和主频的减小程度要比速度高1~3个数量级(曹均等,2004).通过对Gassmann方程的合理简化并引入Esheby-Walsh干燥岩石椭球包体近似公式,推导出包含岩石孔隙结构参数的孔隙度计算公式,实践证明该方法的精度高于常规方法(高刚,2013).利用含有裂隙的有效弹性模量关系与骨架的组合理论建立模型,用于描述波速与孔隙度的关系(陈祖安和伍向阳,2000).基于岩石物理学中临界孔隙度模型,进行了地震波的数值模拟,结合模拟结果分析了孔隙度对地震波传播的影响(郭继亮等,2012).利用地震资料预测孔隙度的广义协克里格法,并应用到松辽盆地宋站地区(孙树海和刘雪莹,1993).
国外学者在Wyllie公式的应用上有存在两种观点,一种认为不该再用此公式计算孔隙度,具有代表性的意见有,Geertsma指出Wyllie 公式未考虑岩石的体积形变,难以在复杂地质条件下应用(Geertsma and Smith, 1961).Russell指出它不适用于含气砂岩孔隙度的预测(Russell et al., 2003).另外一种观点认为针对不同的地层特征应该对Wyllie公式进行一定的修正,Saleh指出常规Wyllie 公式低估了孔隙结构纵横比高的波速,但是又高估了岩化程度低的波速,因此,提供了一种更广泛的时间平均公式形式来描述声波速度与孔隙度之间的关系,将粒间孔和晶间孔归一类孔隙,球形或近球形孔隙归一类分别进行了研究(Saleh and Castagna, 2004).
可以看出,此研究领域在工程资料的深度加工、基础实验研究、数值模拟研究及Wyllie公式适用性问题的探讨上均非常活跃.以此为研究背景,本文将开展孔隙尺寸与孔隙密度对碳酸盐岩地层声波属性与孔隙度相关性影响研究,在此基础上探讨Wyllie公式的适用性并探索基于声波衰减属性的孔隙度预测模型.
1 数值模拟方案
1.1 wyllie时间平均公式物理基础
Wyllie假设岩石满足:具有相对均匀的矿物;被液体饱和;在高有效压力下,声波在岩石中直线传播的时间是在骨架中的传播时间与在孔隙流体中的传播时间的和,以此为基础,根据岩石体积模型: t=tma+tf .
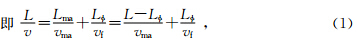


利用有限差分求解二维声波波动方程,再对方程的显式差分近似进行离散化处理,然后设置相应的初始条件、边界条件、收敛条件和震源(陈乔等,2012).
本文主要目的在于模拟室内小岩柱超声波透射物理试验,因此以被测试样品的纵向剖面为模型,设置的小岩柱岩 心模型尺寸为50×25 mm,如图 1,岩心骨架速度为6200 m/s,孔隙中流体速度为340 m/s,通过波速来表征岩石孔隙与骨架的弹性性质.提取实验室超声波探头激发信号作为数值模拟的输入波形,如图 2.将岩心纵向剖面区域划分成500×250的网格,模型空间采样间隔为0.1 mm,数值模拟时间采样间隔为10 ns.应用Matlab编程来实现超声波透射实验模拟.
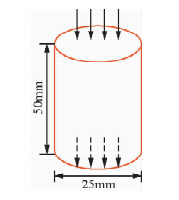 | 图 1 数值模型示意图Fig. 1 Numerical model diagram |
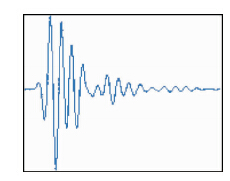 | 图 2 数值计算输入波形图Fig. 2 Numerical calculation input waveform |
Lucia(1995年)和Choquette(1970年)分别按照孔洞尺寸的不同对孔隙进行了分类,见表 1(雍士和和张超谟,1996).
| | 表 1 孔隙分类标准 Table 1 Pore classification criteria |
本文以上表为依据,设计模型参数如表 2的理想数字岩心模型.设计了四个具有代表性的孔隙度,在定孔隙度下通过减小孔洞半径来进行了孔洞密度调整,半径范围为0.315~3.09 mm,模型尺度基本覆盖了中、大孔洞.不同孔隙度,相同孔密度下的孔洞分布位置完全相同,分布方式为均匀随机分布.
| | 表 2 理想数字岩心参数表 Table 2 The parameters of ideal core |
1.4.1 波速的处理
本研究的数值模拟实验,均是提取初至波进行波速计算,如图 3.
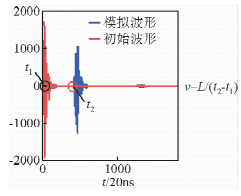 | 图 3 波速计算示意图Fig. 3 Wave velocity calculation schematic diagram |
其中t1是入射波的初至波起跳时间,t2为透射波的初至波起跳时间,L为岩心长度,v是计算得到的初至波波速.
1.4.2 衰减特性的处理
声波品质因素Q值是反映弹性波在岩石中传播衰减程度的重要参数.Q值是储能与耗散能的比率,它作为岩石的一种内凛特性.Q值可在频率域内和时域内计算,其计算方法主要有频谱振幅比法、波形反演法、能量法.
频谱振幅比法要求试件中传播的是平面波,要求试件必须很大.根据国际岩石力学学会对实验室的建议(国际岩石力学学会,1981),试件的最小横向尺寸D(垂直于波的传播方向)应不小于波长L的10倍,即D≥10L.波形反演法要求样品直径足够细可视为杆,具体要求波长与直径的比值大于5,长度与直径的比值大于3.严格来说,只有当样品直径大于80 mm时,才可采用频谱振幅比法;只有当样品直径小于1.6 mm时,才能将样品视为杆.对石油行业而言,实验室待测样品岩心柱长度范围在40~60 mm,其波速约为4000 m/s左右,换能器主频约为100 kHz以上,波长为8 mm左右.
因此本文采用能量法计算Q值.任意测试距离Q值的计算方法为
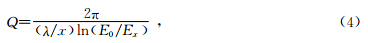
2.1 理想岩样的数值计算分析
图 4为孔隙度为5%时不同孔密下的波场快照图,图 5~图 6为数值计算结果,可以看出定孔隙度情况下随着孔洞尺寸的减小和孔洞密度的增加,声波速度呈现出减小趋势,且这种减小趋势随孔隙度的增加而变大,图中红色虚线为根据wyllie公式进行理论计算得到相应孔隙度下对应的波速理论值,当孔密度0.08~0.064个/mm2时实测孔隙度-波速关系远离wyllie计算值,当孔密度大于0.096个/mm2时,实测孔隙度-波速的关系非常接近wyllie理论计算值.
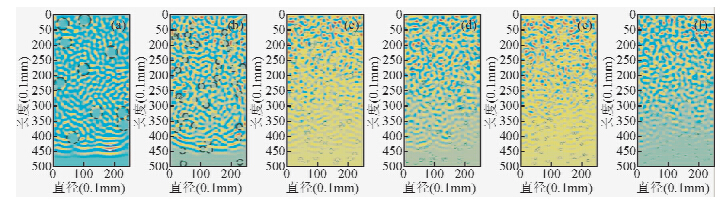 | 图 4 孔隙度为5%时不同孔洞密度波场快照图(a~f孔密度从0.008个/mm2~0.16个/ mm2逐渐变大)Fig. 4 Snap shot of 5% porosity different pore density(pore density gradually becomes larger from0.008~0.16) |
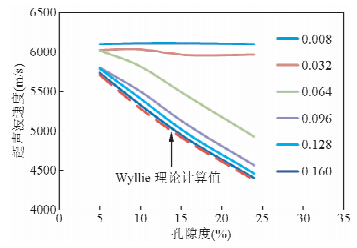 | 图 5 孔隙度-超声波速度关系图Fig. 5 The relationship of porosity and ultrasonic velocity |
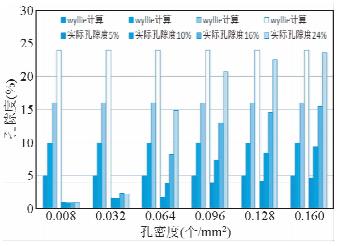 | 图 6 孔密度-孔隙度关系图Fig. 6 The relationship of porosity and pore density |
上述模拟结果说明除了孔洞尺寸外孔洞密度也是影响其超声波传播规律的一个重要因素.当孔洞密度很小,并且很离散时,即使孔洞较大,接受到的初至波信息可能不含有能反映孔洞的信息;当孔洞密度较大,虽然此时孔洞尺寸依然比较大,但是这增加了声波通过孔洞的机率,因此就表现出了图 6的情况.当孔密较小时,不同孔隙度间的波速相差很小,但是当孔密增加后,不同孔隙度间的波速差异就明显增加了.
从上述研究可知,wyllie平均时间公式能否在孔洞型碳酸盐岩地层中适用,不仅由孔洞尺寸决定,而是受到孔洞尺寸及孔洞密度的共同控制.当孔隙尺寸及孔隙密度满足一定要求时wyllie平均公式是适用的,当孔隙尺寸较大且孔洞分布较离散孔隙密度较小时wyllie平均公式就不适用,此时该类地层的孔隙度预测就成了问题,基于此,在前面波速分析的基础上,对波形中涵盖的声波能量信息进行分析,得到结果如图 7~图 8.
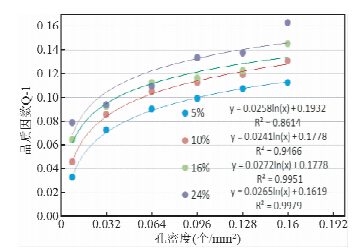 | 图 7 孔密度-品质因数关系图Fig. 7 The relationship of quality factor and pore density |
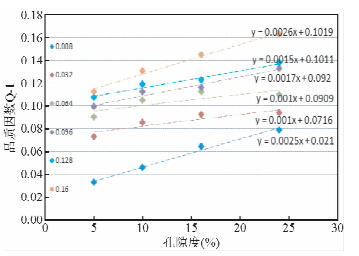 | 图 8 孔隙度-品质因数关系图Fig. 8 The relationship of quality factor and porosity |
由结果图可知,定孔隙度时,孔隙密度-衰减系数呈Q-1=aln(ρ)+b对数规律变化,定孔隙密度时,孔隙度-品质因数呈φ=aQ-1+b线性规律变化.相关性系数大小与孔隙度大小和孔隙密度之间没有明显的关系,但是拟合模型的系数直接受到孔隙密度的影响,孔隙密度越大则b值越大,a值的影响有待进一步研究.这就为孔洞型碳酸盐岩地层孔隙度预测提供了另一种思路,在波速应用效果不好,并且具有波形资料的情况下,可以考虑用衰减特性进行孔隙度的预测,当然由于衰减特性受到多方因素的影响,因此目前应用存在一定困难,但随着全波列测井资料的逐渐推广,衰减特性作为一种储备技术进行前期研究是可行的. 2.2 实际岩样的数值计算分析
上述数值计算是基于一组理想的孔洞模型(实际岩心的重复性较差),在此我们利用四川盆地某地层的一块真实碳酸盐岩岩样进行了基于图像数字处理提取孔隙结构的超声波数值模拟研究,验证上述数值模拟结果的可行性.图片9是岩样的实物照片,从照片可以看出岩心富含离散孔洞,以溶蚀孔洞和粒间孔隙为主,孔洞尺寸变化范围较大,横向最大尺寸达5 mm,最小不过零点几毫米,岩心直径为25 mm,长度为47 mm,孔隙度为0.22.
 | 图 9 实物岩样照片Fig. 9 The kind rock sample photo |
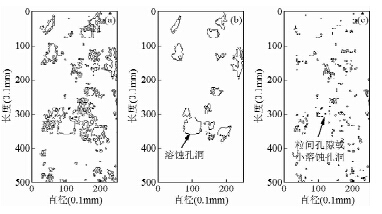 | 图 10 二值化处理并提取孔隙后岩样孔隙结构 (a)模型1;(b)模型2;(c)模型3.Fig. 10 The pore structure after binarization processing and extraction |
以图 9为研究基础,对图中的孔隙和基质骨架区域进行分割、二值化处理及边缘提取得到图 10,建立三个数值模拟物理模型,模型1为实际岩样孔隙结构、模型2以溶蚀孔洞为主、模型3以小溶蚀孔隙和粒间孔隙为主,模型1孔隙度为0.22,模型2和3的孔隙度均为0.11.模型大小以岩心实际直径和长度为基准,网格步长为0.1 mm.
图 10所示的数字图像通过方形单元映射的方法可以很方便地转化成有限差分网格数据,数字图像是由一个矩形排列的像素点组成,每个像素点是一个小正方形,均可作为有限差分计算中的四边形单元.其中每个单元的 4个节点坐标通过图像实际尺寸与像素尺寸之间的比例关系,可以转换为相应矢量空间的物理坐标,整个图像就可转换为正方形有限差分网格,然后根据每个像素点所属灰度值,给每个单元赋予相应的材料参数,从而把数字图像表征的孔隙引入到数值模型中.转化后的数值模型如图 11 所示,图中颜色愈红表示弹性模量愈大,波速越大(Mora et al., 1998;Yue et al., 2003;范留明和李宁,2005;于庆磊等,2010).
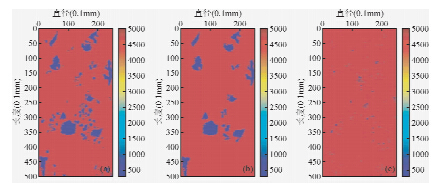 | 图 11 计算模型速度云图 (a)模型1速度云图;(b)模型2速度云图;(c)模型3速度云图.Fig. 11 Calculation model speed nephogram |
图 12~图 14为真实岩心的超声波数值模拟结果.当将岩心中的孔隙结构进行分类处理,分别提取出大孔隙和小孔隙,两部分孔隙度相同而孔隙密度不同,进行超声波数值模拟结果显示,当富含连续性较强的小孔隙时相对饱含离散大孔洞而言,其波速趋近于wyllie理论计算值,与此同时见图 14其衰减大小基本上符合之前理论计算建立的模型.
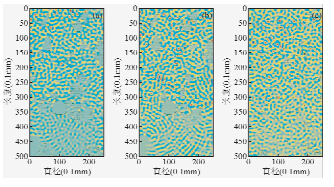 | 图 12 数值计算后的波场快照图 (a)模型1波场快照图;(b)模型2波场快照图;(c)模型3波场快照图.Fig. 12 Snap shot of rock sample |
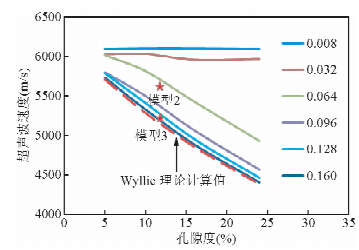 | 图 13 实际岩样与理想岩样速度结果对比分析Fig. 13 A comparative analysis of actual rock samples ideal rock speed |
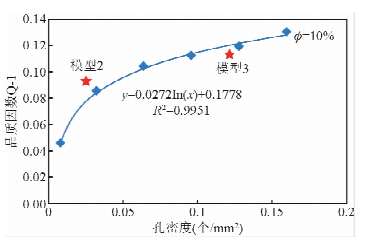 | 图 14 实际岩样与理想岩样品质因数对比分析Fig. 14 comparative analysis of actual rock samples ideal rock quality factor |
通过上述研究,本文得到如下有益结论:
(1)wyllie平均时间公式能否在孔洞型碳酸盐岩地层中适用,不仅由孔洞尺寸决定,而是由孔洞尺寸及孔洞密度共同决定.
(2)当孔密度为0.08~0.064个/mm2时,实测孔隙度-波速关系背离wyllie计算值,当孔密度大于0.096个/mm2时,实测孔隙度-波速的关系趋近于wyllie理论计算值.
(3)定孔隙度时,孔隙密度-衰减系数呈Q-1=aln(ρ)+b的对数规律变化.
(4)定孔隙密度时,孔隙度-衰减系数呈φ=aQ-1+b的线性规律变化.相关性系数大小与孔隙度大小和孔隙密度之间没有明显的关系,但是模型的系数直接受到孔隙密度的影响,孔隙密度越大则b值越大.
建议:
本文是结合超声波数值模拟方法和数字图像处理技术对岩石孔隙度预测进行的探索性研究,证明了该研究方法的可行性,证实孔隙密度是一个关键影响因素,接下的研究中可以对孔隙密度和尺寸进行细化,得到更加准确的模型,对模型系数的影响因素进行单独分析,用实验数据和测井数据进行验证.
致 谢 西南石油大学油气藏地质及开发工程国家重点实验室岩石力学实验室的刘向君教授在本文研究中提供了大量意见并进行指导,在此给予最衷心的感谢!| [1] | Cao J, He Z H, Hang J D, et al. 2004. Physical modeling and Ultrasonic experiment of pore-crack in reservoirs[J]. Progress in Geophysics (in Chinese), 19(2): 386-391, doi: 10.3969/j.issn.1004-2903.2004.02.027. |
| [2] | Chen J H, Xiao L, Mao Z Q. 2011. Method for evaluating porosity in carbonate reservoir with pores and vugs[J]. Journal of Oil and Gas Technology (in Chinese), 33(6): 92-97. |
| [3] | Chen Q, Liu X J, Liang L X, et al. 2012. Numerical simulation of the fractured model acoustic attenuation coefficient[J]. Chinese Journal of Geophysics (in Chinese), 55(6): 2044-2052, doi: 10.6038/j.issn.0001-5733.2012.06.026. |
| [4] | Chen Z A, Wu X Y. 2000. A model for the relation between wave velocity and porosity as well as clay content in sandstone [J]. Progress in Geophysics (in Chinese), 15(1): 78-82, doi: 10.3969/j.issn.1004-2903.2000.01.007. |
| [5] | Fan L M, Li N. 2005. Study on rock mass joint measurement based on digital photogrammetry[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 24(5): 792-797. |
| [6] | Gao G. 2013. Method for predicting the porosity based on the pore structure of carbonate[J].. Progress in Geophysics (in Chinese), 28(2): 920-927, doi: 10.6038/pg20130245. |
| [7] | Geertsma J, Smith D C. 1961. Some aspects of elastic wave propagation in fluid–saturated porous solids[J]. Geophysics, 26(2): 169-181. |
| [8] | Guo J L, Niu B H, Sun C Y, et al. 2012. Seismic wave propagation based on critical porosity model[J]. Chinese Journal of Geophysics (in Chinese), 55(11): 3813-3820, doi: 10.6038/j.issn.0001-5733.2012.11.028. |
| [9] | Jiang J Y. 2004. The porosity interpretation model for carbonate reservoir in Tahe Oilfield[J]. Geophysical Prospecting for Petroleum (in Chinese), 43(6): 564-567. |
| [10] | Jing J E, Mei Z W, Li Z B. 2003. Investigation of well logging evaluation and identification methods for carbonate reservoirs with fracture and vug in Tahe oil field[J].. Progress in Geophysics (in Chinese), 18(2): 336-341, doi: 10.3969/j.issn.1004-2903.2003.02.026. |
| [11] | Le F L, He Z H, Wen X T, et al. 2010. ZH carbonate reservoir porosity prediction method[J]. Oil and Gas Technology(J.JPI) (in Chinese), 32(3): 236-239. |
| [12] | Li S R, Li A H, Qian Q, et al. 2010. An approach to calibrate logging porosity with whole well cores data[J]. Well Logging Technology (in Chinese), 34(6): 572-575. |
| [13] | Li X H, Zhou Y Q, Gou Y H, et al. 2012. Porosity analysis of micro-electric imaging logging and its application in carbonate reservoir production capacity forecast[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 42(4): 928-934. |
| [14] | Mora C F, Kwan A K H, Chan H C. 1998. Particle size distribution analysis of coarse aggregate using digital image processing[J]. Cement and Concrete Research, 28(6): 921-932. |
| [15] | Qi L X, Fan Z J, Li Z J, et al. 2010. Tri-porosity logging model of carbonate reservoir in Tahe Oilfield and its application[J]. Geophysical Prospecting for Petroleum (in Chinese), 49(5): 489-494. |
| [16] | Russell B H, Hedlin K, Hilterman F J, et al. 2003. Fluid-property discrimination with AVO: A Biot-Gassman prospective[J]. Geophysics, 68(1): 29-39. |
| [17] | Saleh A A, Castagna J P. 2004. Revisiting the Wyllie time average equation in the case of near-spherical pores[J]. Geophysics, 69(1): 45-55. |
| [18] | Sun S H, Liu X Y. 1993. Generalized cokriging of porosity prediction from seismic data[J]. Chinese Journal of Geophysics (in Chinese), 36(6): 798-803. |
| [19] | Wu G N, Sun L, Cao S Y. 2013. Impact of porosity on seismic attributes in thinly layered porous media[J]. Progress in Geophysics (in Chinese), 28(3): 1408-1416, doi: 10.6038/pg20130334. |
| [20] | Yong S H, Zhang M C. 1996. Logging Data Processing and Integrated Interpretation (in Chinese)[M]. Dongying: University of Petroleum Press. |
| [21] | Yu Q L, Yang T H, Tang C A, et al. 2010. Actual meso-structure based three-dimensional modeling method for quasi-brittle material and its primary application[J]. Chinese Journal of Computational Mechanics (in Chinese), 27(5): 887-893. |
| [22] | Yue Z Q, Chen S, Tham L G. 2003. Finite element modeling of geomaterials using digital image processing[J]. Computers and Geotechnics, 30(5): 375-397. |
| [23] | Zhang D J, Chen C Y, Wang S J, et al. 2007. Study on relation between core analysis porosities of small samples and that of whole diameter samples in carbonate reservoirs[J]. Well Logging Technology (in Chinese), 31(4): 307-310. |
| [24] | Zhao H, Shi X, Shima L Q. 2012. Study on porosity exponent, saturation and fracture porosity for fractured reservoirs[J]. Progress in Geophysics (in Chinese), 27(6): 2639-2645, doi: 10.6038/j.issn.1004-2903.2012.06.043. |
| [25] | 曹均, 贺振华, 黄德济,等. 2004. 储层孔(裂)隙的物理模拟与超声波实验研究[J]. 地球物理学进展, 19(2): 386-391, doi: 10.3969/j.issn.1004-2903.2004.02.027. |
| [26] | 陈继华, 肖亮, 毛志强. 2011. 溶孔洞型含气碳酸盐岩储层孔隙度评价方法研究[J]. 石油天然气学报, 33(6): 92-97. |
| [27] | 陈乔, 刘向君, 梁利喜,等. 2012. 裂缝模型声波衰减系数的数值模拟[J]. 地球物理学报, 55(6): 2044-2052, doi: 10.6038/j.issn.0001-5733.2012.06.026. |
| [28] | 陈祖安, 伍向阳. 2000. 砂岩孔隙度和含泥量与波速关系的模型[J]. 地球物理学进展, 15(1): 78-82, doi: 10.3969/j.issn.1004-2903.2000.01.007. |
| [29] | 范留明, 李宁. 2005. 基于数码摄影技术的岩体裂隙测量方法初探[J]. 岩石力学与工程学报, 24(5): 792-797. |
| [30] | 高刚. 2013. 基于碳酸盐岩孔隙结构预测孔隙度方法研究[J]. 地球物理学进展, 28(2): 920-927, doi: 10.6038/pg20130245. |
| [31] | 郭继亮, 牛滨华, 孙春岩,等. 2012. 基于临界孔隙度模型的地震波传播[J]. 地球物理学报, 55(11): 3813-3820, doi: 10.6038/j.issn.0001-5733.2012.11.028. |
| [32] | 将进勇. 2004. 塔河油田碳酸盐岩储层孔隙度模型的改进[J]. 石油物探, 43(6): 564-567. |
| [33] | 景建恩, 梅忠武, 李舟波. 2003. 塔河油田碳酸盐岩缝洞型储层的测井识别与评价方法研究[J]. 地球物理学进展, 18(2): 336-341, doi: 10.3969/j.issn.1004-2903.2003.02.026. |
| [34] | 雷芬丽, 贺振华, 文晓涛,等. 2010. ZH区碳酸盐岩储层孔隙度预测方法研究[J]. 石油天然气学报(江汉石油学院学报), 32(3): 236-239. |
| [35] | 李淑荣, 李爱华, 钱勤,等. 2010. 利用全直径岩心刻度测井孔隙度方法探讨[J]. 测井技术, 34(6): 572-575. |
| [36] | 李晓辉, 周彦球, 缑艳红,等. 2012. 电成像测井孔隙度分析技术及其在碳酸盐岩储层产能预测中的应用[J]. 吉林大学学报(地球科学版), 42(4): 928-934. |
| [37] | 漆立新, 樊政军, 李宗杰,等. 2010. 塔河油田碳酸盐岩储层三孔隙度测井模型的建立及其应用[J]. 石油物探, 49(5): 489-494. |
| [38] | 孙树海, 刘雪莹. 1993. 用地震资料预测孔隙度的广义协克里格法[J]. 地球物理学报, 36(6): 798-804. |
| [39] | 武国宁, 孙娜, 曹思远. 2013. 层状孔隙介质孔隙度对地震属性影响分析[J]. 地球物理学进展, 28(3): 1408-1416, doi: 10.6038/pg20130334. |
| [40] | 雍士和, 张超谟. 1996. 测井数据处理与综合解释[M]. 东营: 石油大学出版社. |
| [41] | 于庆磊, 杨天鸿, 唐春安,等. 2010. 基于真实细观结构的准脆性材料三维建模及应用初探[J]. 计算力学学报, 27(5): 887-893. |
| [42] | 张豆娟, 陈存元, 王善江,等. 2007. 碳酸盐岩储层小岩样与全直径岩心分析孔隙度关系研究[J]. 测井技术, 31(4): 307-310. |
| [43] | 赵辉, 石新, 司马立强. 2012. 裂缝性储层孔隙指数、饱和度及裂缝孔隙度计算研究[J]. 地球物理学进展, 27(6): 2639-2645, doi: 10.6038/j.issn.1004-2903.2012.06.043. |
 2015, Vol. 30
2015, Vol. 30


