2. 中石化胜利油田石油开发中心, 东营 257000
2. Petroleum Development Center of Sinopec Shengli Oilfield, Dongying 257000, China
全波形反演(FWI)是一种利用地震数据的全部信息以获得高分辨率地下介质模型的数据拟合方法.最初,Lailly(1983),Tarantola(1984,1987),Mora(1987,1988)等人将梯度类全波形反演算法引入勘探地球物理领域,目前其已经成为地球物理学家的研究热点(Shin and Min, 2006;任浩然,2011; 任浩然等,2013;Biondi and Almomin, 2013;杨午阳等,2013;董良国等,2013;刘璐等,2013;魏哲枫等,2014).
全波形反演可以在时域或频域实现.频域全波形反演(Sirgue and Pratt, 2004;Operto et al., 2007;卞爱飞等,2010;高凤霞等,2013;廖建平等,2014)需要应用大型稀疏矩阵的LU分解,对于炮数较多的地震数据较为有效,但需要较大的存储空间,适用于2D或者小3D反演问题(Operto et al., 2007),另一个优势是有可能仅仅需要选取一系列频率进行反演,但这取决于目标深度和最大偏移距(Sirgue and Pratt, 2004),然而对于实际观测系统而言,大多数地质目标体埋深大且偏移距小,一般需要十几到几十个频率,这使得时域全波形反演更具吸引力.时域全波形反演,由于需要进行成千上百次迭代计算,需要研究快速的正演算法,其实现过程简单,需要的计算内存少.缺点是如果正演中的时间间隔较小或者需要计算多炮数据,尤其是3D,需要耗费大量的计算时间.时域方法由于需要同时反演低频和高频信息存在“跳周”(cycle-skipping)现象,并且由于梯度计算中的时间导数问题,低频估计也是一个较大的问题(Sirgue and Pratt, 2004).
本文以时域全波形反演原理为基础,首先分析了数据完备性、数据噪声、正问题(正问题表征、震源子波、边界及频散等)、初始模型、正则化以及多尺度等因素对时域全波形反演的影响,然后探索了加入井数据约束的反演策略,给出了相应的井约束全波形反演误差泛函与梯度计算公式以及CPU并行实现流程,利用复杂地震地质模型验证了方法的正确性. 1 时域全波形反演基本原理
常密度声介质波动方程可以表示为

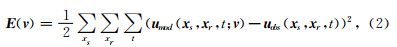

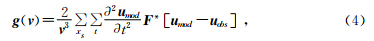
利用共轭梯度修正因子为β修正梯度,设置共轭梯度为 ψ,ψ0=-g0,则有
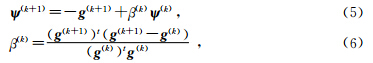

地震观测记录中包含有地球介质中岩石物性参数及地下构造信息,能够较为真实地反映地震波在地下传播的规律,但也受到很多因素的影响,限制了地震勘探的分辨率、保真度和精度.因此,在全波形反演中,研究各个因素对反演结果的影响是非常必要的:一则可以将不利的影响因素消除或者降至最低,二则可以将有利的影响因素进行优化或者放大,以使有利因素和不利因素之间达到最佳的匹配和均衡状态,从而获得最佳的、具有合理地球物理意义的、符合地下真实地质情况的全波形反演结果. 2.1 数据完备性
由于地震勘探野外观测系统设计的限制,一般来说,得到的地震记录都是有限观测孔径的数据,包括地面激发地面接收的地面地震、地面激发井中接收的VSP、井中激发地面接收的逆VSP以及井中激发井中接收的井间地震.这些观测方式有一个共同的特点:数据都是不完备的.但是,长期以来应用的观测系统就是这样的,有些数据又不方便进行二次采集,这就给全波形反演带来了较大的困难.查阅近年来全波形反演文献中的实例可以发现:大多数观测系统设计均为长排列、宽方位角采集.这种采集方式不难解释:首先,时域全波形反演对低频成分的要求较高,长排列大偏移距地震记录包含了丰富的低频信息,能够为全波形反演提供好的背景速度场;其次,宽方位角采集增加了数据的完备程度,这对于全波形反演是非常有用的.
因此,在全波形反演应用之前,做好与之相关的观测系统设计及优化是非常必要的.可以通过波动方程双向照明分析实现观测系统优化设计,优化设计的内容主要包括:炮点个数及间距,检波点个数及偏移距、检波间距,总排列长度等(陈永芮等,2013),另外,从目的层出发在地面接收的双向照明分析能够很大程度上优化观测系统设计,使得全波形反演的能量尽可能多地到达目标区,获得针对目标区的高精度反演结果. 2.2 数据噪声
地震勘探中的噪声可以划分为相干噪声和非相干噪声.相干噪声包括面波、特殊构造产生的反射波、折射波和多次波等,其可以在地震道上识别、压制或者消除.非相干噪声往往是指随机噪声,具有空间随机性和不可预测性,一种是可重复随机噪声,主要是由异常体和不均匀体的散射造成的,能量小;另一种是不可重复随机噪声,主要是由风吹草动或者检波器附近人员走动等原因产生的.
在波形反演中,需要将野外观测数据与正演模拟数据进行拟合,噪声的存在会使得后续的反演求解产生迭代累积误差,污染甚至破坏整个反演过程的稳定性和收敛性.当然,这里所指的噪声跟常规地震勘探中的噪声有所不同,从广义上讲,波形反演中的噪声主要包含两种情况:①观测数据中不能利用波动方程正演模拟表征的波现象或者信号,②正演模拟过程中产生的边界反射和数据误差;第二种情况已经作为正问题进行了分析,此处不再赘述.以下将重点针对第一种情况(即观测数据中不能利用正演模拟表征的波现象或信号),提出可行的实用化方案:首先,要弄清楚全波形反演是基于哪种理论的波动方程进行正演模拟的,以确定正演过程中可以表征的波型(或者信号)类型;其次,针对特定的波现象和波型信息,研究相应的噪声压制或消除方法;最后,在最大程度保证有效信号(正演过程能够模拟的信号)的前提下,进行噪声压制或者消除. 2.3 正问题
全波形反演中,正问题贯穿于计算的始终.当然,这个正问题的范畴不仅仅是单纯的正演模拟,其包含了声介质波动方程正向传播和反向传播的整个过程.正问题中主要涉及:正问题的描述与表征、震源子波估计与反演、正问题的边界条件及频散等.
(1)正问题的描述与表征
地震波在地下介质中的传播是很复杂的,并不是当前任何形式的波动方程所能够描述的.前面已经说过,如果在工程中采用某种近似手段获取一个问题的最优解(并不一定是真实解),就认为解决了该问题,全波形反演就是在这样的假设框架下实施的.首先,选取能够合理描述或表征地下真实介质中地震波传播规律的波动方程,即确定正问题的表征方式,在此框架下进行全波形反演的公式推导与等价近似,然后利用其振幅和旅行时信息来恢复地下速度构造.王华忠教授等提出了一种特征波形反演,意在利用能够表征地震波传播主要成分的一种正传播算子进行全波形反演,作者认为是一种很好的思路,但是具体实现中存在的诸多问题有待进一步探讨和研究.
(2)震源子波估计与反演
震源子波估计是全波形反演中较为关键的步骤.地震子波估计不准,会对地震记录的波形和旅行时产生较大影响,严重损坏反演中数据拟合的质量. 针对震源子波的估计与反演问题,国内外专家学者提出了很多方法,总结起来不外乎两类:一类是利用原始叠前数据进行子波估计(各商业软件也有相应的模块);另一类是利用全波形反演从原始叠前数据中反演子波,或者进行速度与子波的联合反演.无论采用什么样的方法,都需要根据具体问题进行分析,以优选一种合理、可行、有效的子波估计或者反演方法用于实现全波形反演.
(3)正问题的边界条件及频散
时域正演模拟中,边界条件和频散的影响会对全波形反演产生较大的累积误差,以至于将这种累积效应引入后续的数据拟合环节,使得计算噪声污染整个反问题的搜索方向及收敛速度.通过全波形反演公式推导可以发现,与逆时偏移不同,由于边界条件和频散影响带来的数值误差不会由于干涉效应得到一定程度的消除,而是全部累积到更新梯度以及误差泛函的计算中,对其后的迭代过程产生很大的负面影响.因此,一定要细致处理全波形反演中正问题的边界条件及频散问题. 2.4 初始模型
全波形反演本质上的强非线性性质,要求输入一个较为准确的初始速度,以避免出现“跳周”(cycle-skipping)现象.何谓“跳周”现象?所有应用梯度类方法的全波形反演需要提供一个长波长速度模型(即低频成分),使得观测记录与正演记录差值控制在半个主波长范围内以保证其能够收敛到全局极小值(图 1).全波形反演中,这种观测数据与模型数据的强非线性现象,称之为周波跳跃或者跳周.
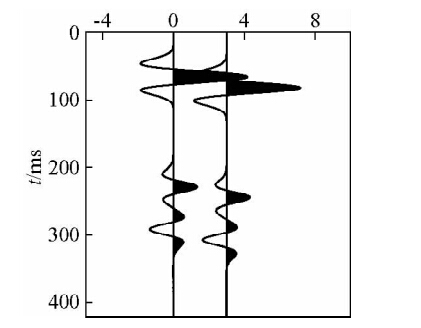 | 图 1 半波长范围内的观测记录与正演记录Fig. 1 Observational record and modeling record in half-wavelength |
换一个角度来看,初始模型也是提供给全波形反演的一种先验约束.虽然其在数学上具有很完美的理论基础,但是在缺乏先验约束的情况下它将一事无成.可以这么说,初始速度模型的准确程度直接控制着全波形反演的成败,因此如何获取一个避免出现“跳周”的初始速度模型变得尤为重要.好的初始模型能够使全波形反演在迭代较少次数后较快地收敛到真实解附近.以下分析不同初始模型对全波形反演的影响.
为了测试初始模型的影响,本节截取Marmousi的浅层进行数值试算.速度模型纵横向采样点数分别为350和737,纵横向间距均为5 m,地表放炮,炮数50炮,第一炮位置500 m,炮间距55 m,地表全孔径接收,采用25 Hz的雷克子波激发. 得到的炮记录时间采样点数4001,时间采样率0.5 ms,记录长度2 s.分别采用两个不同平滑度和一个常梯度初始模型进行数值模拟试算,其中平滑初始模型是利用Seismic Unix里面的smooth2命令进行平滑,平滑因子分别选取r1=r2=40以及r1=r2=70.图 2a是Marmousi真实模型,分别利用图 2b、图 2d和图 2f所示的初始模型进行FWI试算,其迭代70次后的反演结果显示在图 2c、图 2e和图 2g中.
 | 图 2 Marmousi模型不同初始模型全波形反演数值试算Fig. 2 FWI numerical tests of Marmousi model with different initial velocity models |
根据图 2所示的反演结果,可以得到如下的结论:利用常梯度速度作为初始模型进行迭代反演得到的结果最差,平滑因子为70的初始模型得到的反演结果精度居中,平滑因子为40的初始模型得到的反演结果精度最高,但是平滑因子为40和70时的初始速度得到的反演结果精度相差不大.究其原因,可以有如下解释:平滑速度模型是一种比较好的初始模型,因为速度构造中的低频成分保留得较为完整,高频成分可以通过迭代过程得到较好地恢复.图 2c和图 2e浅部构造反演结果相差不大,但是深度构造细节的恢复情况,前者要优于后者.而图 2g所示的常梯度初始模型获得的反演结果,与平滑初始速度模型的反演结果相差较大,这主要是由于其低频成分不够准确使得最终的反演结果难以收敛到真实解. 2.5 正则化
地震全波形反演问题是一个典型的非线性病态问题:①地震勘探的观测方式造成数据的不完备性,由于观测系统的限制,不可能得到地下所有投影角度的观测数据,因此其反过程会产生解的不适定性;②模型空间不同分量的不确定性不同(即观测数据对模型参数的分辨能力不同),这些分量有的是超定的,易于收敛,有的是欠定的,不确定性强,在反演中很难收敛,更甚至有些是零空间分量,依靠现有的观测数据根本无法将其反演出来.这些问题是全波形反演与生俱来的先天缺陷,只能通过一些方法加以约束和改善,使得全波形反演能够为解决实际问题提供帮助.地震处理和反演中常用的方法就是正则化.
正则化方法的选取在很大程度上依赖于所研究问题的特质以及预期加入的地球介质的特定分量.因此可以说,正则化在某种程度上具有较大的主观性.以下总结几种地震全波形反演中常用的正则化方法:
(1)Tikhonov正则化:
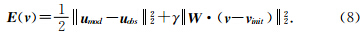
(2)总变差正则化:
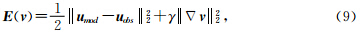
(3)模型参数化方式的正则化问题
用来离散空间连续介质模型的基函数在反演问题的正则化中发挥着重要作用,因为它们事先确定了模型的种类.例如,选择诸如调和函数的谱基准就相当于施加了平滑约束,不再允许模型中有突变特征存在.
由于全波形反演旨在恢复强反射面,因此需要用到局部基函数.对于优化正则化而言,需要将基函数调整为对可分辨波长的先验估计,这将有助于避免不可分辨的短波长扰动.这种全球范围自适应离散方法已经被很多学者证实(Debayle and Sambridge, 2004;Nolet and Montelli, 2005).在区域范围内,尤其是全波形反演,利用离散进行数值模拟来研究地球介质是很自然的事情.例如,Tape等人(2010)利用Lagrange多项式基函数来实现谱元模拟.这种方法的参数化方式能够自动调整为地震波的波长,并且至少在覆盖次数较多的区域同预期可分辨波长大致吻合.
(4)迭代次数选取的正则化问题
这是一种难以量化的正则化方式,其通过有限次迭代以估计最优化模型参数.随着非线性反演由一个模型变换到另一个模型,误差泛函不断减小.在这个过程中,数据奇异值逐渐变成主控因素,会引入很多假象,因此反演需要在迭代一定次数后结束,当然这个一定的次数需要反演人员进行操控.虽然这种正则化方式常常被人忽略,但是却是非线性反问题中一个非常重要的内容.
综上所述,正则化就是反演人员给全波形反演提供的一种约束和预期,目的是让其沿着这种先验约束和预期逐步获得一个精确度较高的反演结果. 2.6 多尺度问题
时域全波形反演的强非线性极易导致反演解陷入局部极值,这就要求对模型进行多尺度分析.多尺度思想可以将反演在不同尺度上实施,尽量避免局部极小值问题.目前,时域多尺度全波形反演主要是基于时间域多重网格实现的,经典的实现方案是由Bunks等人建立起来的,基于速度网格的不同剖分层次来实现多尺度反演(Bunks,1995;刘雅宁等,2014):首先,利用大的空间网格,限定数据频带范围以满足稳定性,计算大尺度上的宏观背景速度.其次,利用更新速度作为下一尺度反演的输入,通过逐步缩小速度网格大小来达到多尺度反演的目的. 3 井数据约束探索 3.1 井数据约束基本原理
对于地震勘探实际工区而言,能够利用的先验约束主要有:先验地震信息、测井数据信息以及对工区主要目的层的地质构造认识.其中,测井数据被认为是较准确、可靠的先验信息,尤其是与地层慢度对应的声波时差测井曲线,可以用来作为先验约束加入到时域全波形反演误差泛函正则化项的构建中.基于以上考虑,可以构建如下的井约束全波形反演误差泛函表达式:
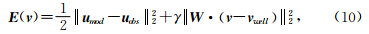
对应的速度更新梯度 g(v)可以写为
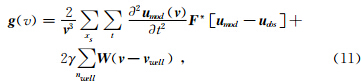
(1)正则化矩阵W的求取
以井位点所在横向位置为基准,采用指数衰减形式构建归一化的正则化矩阵,即井位点A所在横向位置处对正则化贡献最大,其矩阵元素设置为wA=1,其附近任一位置B处采用如下的指数函数计算矩阵元素:wB=(fac)m,该处底数fac满足0
(2)正则化因子γ的选取
由公式(10)可以看出:正则化因子γ的作用主要就是调节纯数据误差泛函项 基于CPU并行实现的井约束全波形反演技术路线(图 3)可以概括为:
(1)初始模型的获取.本文采用基于角道集的层析速度反演获得的深度域速度场作为初始速度模型输入.
(2)速度更新梯度的并行计算.首先,在初始模型中计算正传播波场,并通过观测炮记录与模型炮记录的求差运算获取炮记录残差;其次,将炮记录残差和正传波场分别进行反向传播(采用计算换取存储的策略),求取单炮梯度,等待所有炮计算完毕,利用规约算子将所有炮的结果进行叠加获取总的速度更新梯度,通过公式(11)加入井约束正则化项.
(3)迭代更新步长的并行计算.给定一个试探步长,求得一个伪速度模型,基于伪速度模型进行有限差分正演计算(炮并行)并求取总的记录残差以得到优化的迭代步长,然后实现速度更新,通过迭代条件的判断确定是否需要进一步迭代.若不满足迭代终止条件,则返回步骤(2)继续循环,若已经满足要求,则输出最终的反演结果.
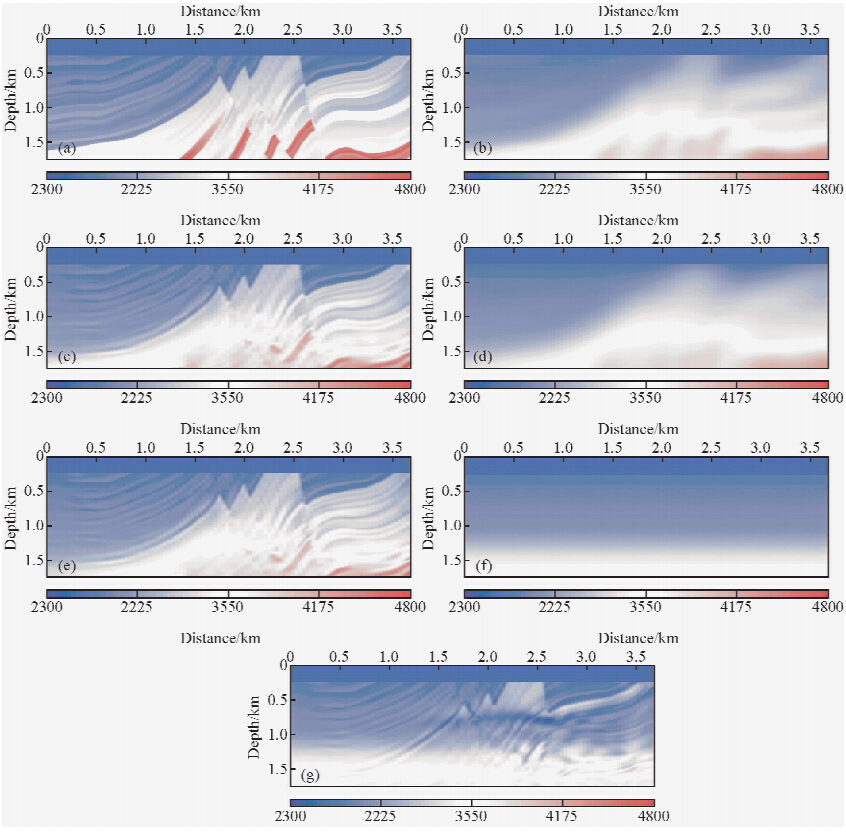
其中,迭代终止条件一般有这样两个:一是迭代次数的控制.这个需要根据经验以及实验试算来获取一个大致的迭代次数,超过这个迭代次数反演就会朝着“过收敛”方向发展,这个时候更多的迭代次数反而会使反演结果更差.二是迭代收敛性准则.可以表示为 利用复杂地震地质模型对井数据约束全波形反演进行模型试算.基于计算效率的考虑,此处对该模型进行了深度截短和重采样.速度网格大小(nx×nz)为1041×566,纵横向网格采样间距分别为8 m,观测系统采用地面放炮地面接收,56炮激发,炮间距80 m,第一炮的位置为1600 m处,地表全孔径接收,检波间距为8 m.震源子波采用25 Hz的Ricker子波,炮记录采样率0.5 ms,记录长度3 s.模型表层的一系列薄层设为一套大层,内部的极薄层不变,初始模型为成像域走时层析反演进行了平滑的速度场.采用模型Distance=3 km和5 km处的真实速度作为井约束数据.
图 4a为地震地质模型速度场,图 4b所示为利用角道集走时层析获得的反演速度场经过平滑以后得到的,可以看到背景低频速度分量都已经得到了较好的恢复,构造模糊可见,这样的速度场作为初始速度输入是符合全波形反演对于初始速度的条件要求的.利用加入井约束的误差泛函公式(10)进行全波形反演,该处设置的井约束参数如下:fac=0.85,γ=1×10-4.经过40次迭代以后,得到如图 4c所示的井数据约束全波形反演速度场,可以看到:浅层大套层段里面的极薄层得到了很精确的刻画,中间部分逆冲断裂中的薄层也得到了准确的恢复,右侧的地层尖灭形态和轮廓清晰,只有最左边断层下盘里面的薄层恢复得较差,究其原因主要是由于边界处覆盖较少造成的照明不足,以及上盘处的照明遮蔽效应.图 4d为Distance=3 km和5.05 km处真实速度、层析反演平滑速度、未加井约束FWI速度以及井约束FWI速度的对比图,可以得到结论:走时层析反演速度经过平滑以后可以作为较好的全波形反演初始速度,与未加井约束FWI速度相比,井约束反演速度同真实速度吻合度更高,并且靠近井位处的反演精度高于远离井位处的反演精度,验证了方法的正确性.
以声波时域全波形反演原理为基础,分析了数据完备性、数据噪声、正问题(正问题表征、震源子波、边界及频散等)、初始模型、正则化以及多尺度等因素对时域全波形反演的影响,并提出了相应的实用化建议;探索了加入井数据约束的反演策略,给出了相应的井约束全波形反演误差泛函与梯度计算公式以及CPU并行实现流程,利用复杂地震地质模型分析验证了方法的正确性.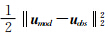 与井数据约束项
与井数据约束项 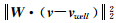 两者权重的一个参数,该因子采用试算法进行选取.试算方式为:分别计算公式(10)中的纯数据误差泛函项
两者权重的一个参数,该因子采用试算法进行选取.试算方式为:分别计算公式(10)中的纯数据误差泛函项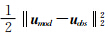 和正则化项
和正则化项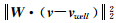 ,以及公式(11)中纯梯度项
,以及公式(11)中纯梯度项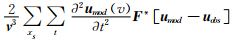 和正则化项
和正则化项 ,分析其数量级并选定一个合适的正则化因子γ.一般而言,正则化项最大不超过相应纯数据误差泛函项(或者纯梯度项)的10 %.
3.2 CPU并行井约束全波形反演的实现
,分析其数量级并选定一个合适的正则化因子γ.一般而言,正则化项最大不超过相应纯数据误差泛函项(或者纯梯度项)的10 %.
3.2 CPU并行井约束全波形反演的实现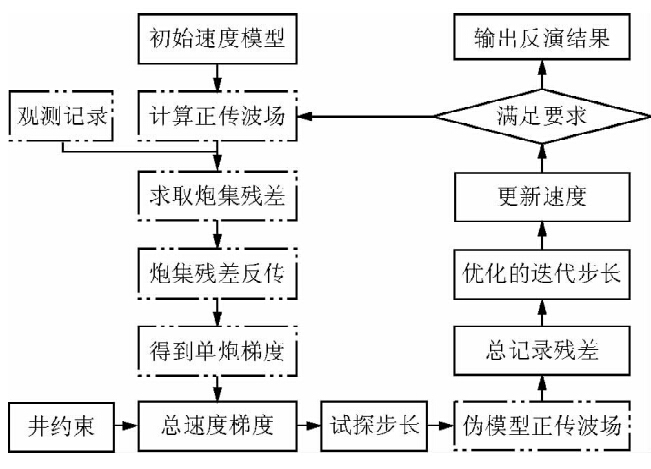
图 3 CPU并行井约束全波形反演流程图
(虚线框表示CPU并行部分)Fig. 3 Flowchart of FWI with well-constraint based on CPU parallel implementation
(The dashed box in this picture is carried out by CPU parallel)
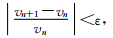
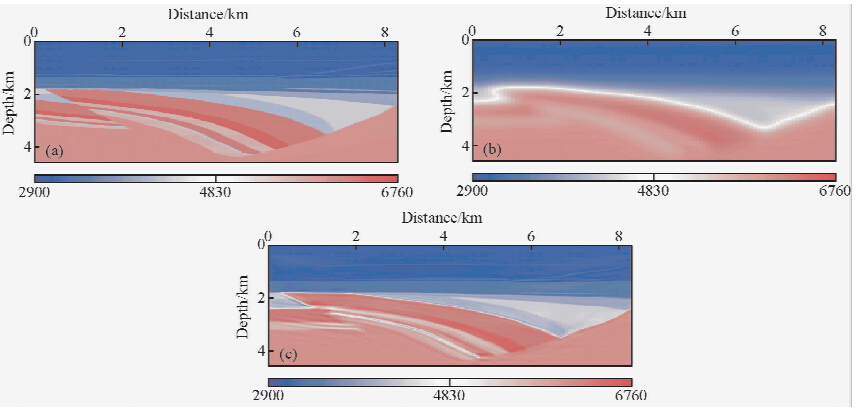
图 4 地震地质模型井数据约束全波形反演数值试算Fig. 4 FWI numerical test of seismic geology model with well constraint
| [1] | Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics (in Chinese), 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [2] | Biondi B, Almomin A. 2013. Tomographic full waveform inversion (TFWI) by extending the velocity model along the time-lag axis[C].//SEG Technical Program Expanded Abstracts, 1031-1036. |
| [3] | Bunks C, Saleck F M, Zaleski S, et al. 1995. Multiscale seismic waveform inversion[J]. Geophysics, 60(5): 1457-1473. |
| [4] | Chen Y R, Li Z C, Qin N, et al. 2013. Full waveform inversion with wave equation bi-directional illumination optimization[J]. Progress in Geophysics (in Chinese), 28(6): 3015-3021, doi: 10.6038/pg2013 0624. |
| [5] | Debayle E, Sambridge M. 2004. Inversion of massive surface wave data sets: model construction and resolution assessment[J]. J. Geophys. Res., 109(B2), doi: 10.1029/2003JB002652. |
| [6] | Dong L G, Chi B X, Tao J X, et al. 2013. Objective function behavior in acoustic full-waveform inversion[J]. Chinese Journal of Geophysics (in Chinese), 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [7] | Gao F X, Liu C, Feng X, et al. 2013. Comparisons and analyses of several optimization methods in the application of frequency-domain full waveform inversion[J]. Progress in Geophysics (in Chinese), 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [8] | Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations[A].//Bednar B J, ed. Conference on Inverse Scattering-Theory and Application[M]. Tulsa: Society for Industrial and Applied Mathematics (SIAM), 206-220. |
| [9] | Liao J P, Liu H X, Zheng G J, et al. 2014. Research on multiscale iterative three dimensional acoustic wave full waveform velocity inversion in frequency-space domain-theoretical model[J]. Progress in Geophysics (in Chinese), 29(1): 204-208, doi: 10.6038/pg20140128. |
| [10] | Liu L, Liu H, Zhang H, et al. 2013. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2447-2451, doi: 10.6038/cjg20130730. |
| [11] | Liu Y N, Liu G F, Zang Z F. 2014. Multiscale computation problem in seismic wave propagation and imaging[J]. Progress in Geophysics (in Chinese), 29(1): 122-128, doi: 10.6038/pg20140116. |
| [12] | Mora P. 1987. Nonlinear two-dimensional elastic inversion of multioffset seismic data[J]. Geophysics, 52(9): 1211-1228. |
| [13] | Mora P. 1988. Elastic wave-field inversion of reflection and transmission data[J]. Geophysics, 53(6): 750-759. |
| [14] | Nolet G, Montelli R. 2005. Optimal parametrization of tomographic models[J]. Geophys. J. Int., 161(2): 365-372. |
| [15] | Operto S, Virieux J, Amestoy P, et al. 2007. 3D finite-difference frequency-domain modeling of visco-acoustic wave propagation using a massively parallel direct solver: A feasibility study[J]. Geophysics, 72(5): SM195-SM211. |
| [16] | Plessix R E. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophys. J. Int., 167(2): 495-503. |
| [17] | Ren H R. 2011. A study of the seismic wave inversion method for imaging in the acoustic media[Ph. D. thesis]. Shanghai: Tongji University. |
| [18] | Ren H R, Huang G H, Wang H Z, et al. 2013. A research on the Hessian operator in seismic inversion imaging[J]. Chinese Journal of Geophysics (in Chinese), 56(7): 2429-2436, doi: 10.6038/cjg20130728. |
| [19] | Shin C, Min D J. 2006. Waveform inversion using a logarithmic wavefield[J]. Geophysics, 71(3): R31-R42. |
| [20] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 69(1): 231-248. |
| [21] | Tang Y X, Lee S W, Baumstein A, et al. 2013. Tomographically enhanced full wavefield inversion[C].//SEG Technical Program Expanded Abstracts, 1037-1041. |
| [22] | Tape C, Liu Q Y, Maggi A, et al. 2010. Seismic tomography of the southern California crust based on spectral-element and adjoint methods[J]. Geophys. J. Int., 180(1): 433-462. |
| [23] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 49(8): 1259-1266. |
| [24] | Tarantola A. 1987. Inverse problem theory: Methods for data fitting and model parameter estimation[M]. 2nd ed. University of California: Elsevier. |
| [25] | Wei Z F, Gao H W, Zhang J F. 2014. Time-domain full waveform inversion based on an irregular-grid acoustic modeling method[J]. Chinese Journal of Geophysics (in Chinese), 57(2): 586-594, doi: 10.6038/cjg20140222. |
| [26] | Yang W Y, Wang X W, Yong X S, et al. 2013. The review of seismic Full waveform inversion method[J]. Progress in Geophysics (in Chinese), 28(2): 766-776, doi: 10.6038/pg20130225. |
| [27] | 卞爱飞, 於文辉, 周华伟. 2010. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993, doi: 10.3969/j.issn.1004-2903.2010.03.037. |
| [28] | 陈永芮, 李振春, 秦宁,等. 2013. 波动方程双向照明优化的全波形反演[J]. 地球物理学进展, 28(6): 3015-3021, doi: 10.6038/pg20130624. |
| [29] | 董良国, 迟本鑫, 陶纪霞,等. 2013. 声波全波形反演目标函数性态[J]. 地球物理学报, 56(10): 3445-3460, doi: 10.6038/cjg20131020. |
| [30] | 高凤霞, 刘财, 冯晅,等. 2013. 几种优化方法在频率域全波形反演中的应用效果及对比分析研究[J]. 地球物理学进展, 28(4): 2060-2068, doi: 10.6038/pg20130450. |
| [31] | 廖建平, 刘和秀, 郑桂娟,等. 2014. 基于多尺度迭代求解三维频率-空间域声波方程的全波形速度反演研究-理论模型[J]. 地球物理学进展, 29(1): 204-208, doi: 10.6038/pg20140128. |
| [32] | 刘璐, 刘洪, 张衡,等. 2013. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 56(7): 2447-2451, doi: 10.6038/cjg20130730. |
| [33] | 刘雅宁, 刘国峰, 张致付. 2014. 地震波传播和成像中的多尺度计算问题[J]. 地球物理学进展, 29(1): 122-128, doi: 10.6038/pg20140116. |
| [34] | 任浩然. 2011. 声介质地震波反演成像方法研究[博士论文]. 上海: 同济大学. |
| [35] | 任浩然, 黄光辉, 王华忠,等. 2013. 地震反演成像中的Hessian算子研究[J]. 地球物理学报, 56(7): 2429-2436, doi: 10.6038/cjg20130728. |
| [36] | 魏哲枫, 高红伟, 张剑锋. 2014. 基于非规则网格声波正演的时间域全波形反演[J]. 地球物理学报, 57(2): 586-594, doi: 10.6038/cjg20140222. |
| [37] | 杨午阳, 王西文, 雍学善,等. 2013. 地震全波形反演方法研究综述[J]. 地球物理学进展, 28(2): 766-776, doi: 10.6038/pg20130225. |
 2015, Vol. 30
2015, Vol. 30

