地球物理学进展  2015, Vol. 30 Issue (1): 165-170   PDF    
引用本文
王维红, 李莹, 张振. 反假频时延Radon变换多次波压制方法研究[J]. 地球物理学进展, 2015, 30(1): 165-170, doi: 10.6038/pg20150125  
WANG Wei-hong, LI Ying, ZHANG Zhen. Investigation on multiple suppression by anti-aliased delay time Radon transform. Progress in Geophysics, 2015, 30(1): 165-170, doi: 10.6038/pg20150125   
反假频时延Radon变换多次波压制方法研究
王维红, 李莹, 张振    
东北石油大学地球科学学院, 大庆 163318
收稿日期: 2014-11-10 修回日期: 2015-01-06 .
基金项目：国家自然科学基金项目(41474118)和国家“863”高技术研究发展计划项目(2012AA061202)联合资助.
作者简介：王维红, 男, 1975年生, 博士, 副教授, 主要从事地震资料数字处理方面的研究.(E-mail: wwhsy@sina.com)
摘要：多次波压制是地震数据处理的重要环节之一, 而Radon变换方法以其优势被广泛应用于多次波处理环节中.本文提出利用时间延迟量Γ代替传统抛物Radon变换的曲率参数q, 对地震记录同相轴进行积分运算.当使用时延Radon变换时, 输入数据的道数作为重要参数直接影响Radon变换域的假频, 而非传统抛物Radon变换空间方向的采样间隔.使用预条件算子通过重建间接增加输入数据的道数, 消除Radon域的假频问题, 提高成像精度, 进而更好的实现多次波压制.利用本文方法对水平层状介质和复杂模型数据进行试算, 结果表明, Radon域假频得到有效抑制, 多次波压制效果明显.
关键词： 时延Radon变换     时间延迟量     多次波压制     反假频    
Investigation on multiple suppression by anti-aliased delay time Radon transform
WANG Wei-hong, LI Ying, ZHANG Zhen    
Geoscience Institute of Northeast Petroleum University, Daqing 163318, China
Abstract: Multiple suppression is one of key steps in seismic data processing, Radon transform is popular and widely used in multiple suppression in seismic data pre-processing. The curvature parameter q is substituted by time-delay value Γ during the course of integral algorithm in the proposed approach in this paper. The artifacts in the time-delay Radon domain is decided by the trace number in the input CMP or shot records, but not the spatial interval along offset direction in the traditional Radon transform algorithm. To decrease the artifact, and also to improve the precision of imaging in the transform domain, the pre-condition operator is used in the proposed method, and then the better result is acquired for multiple suppression. The simple and complex forward modeling shot records are tested for multiple suppression using time-delay Radon transform, the results demonstrated that the proposed approach is anti-aliased, and the primary is preserved better after multiple suppressing.
Key words: time-delay Radon transform     time-delay value     multiple suppression     anti-alias    
0 引 言

基于一次波与多次波之间的时差差异，可利用抛物Radon变换方法有效地实现多次波压制，但在实际应用时也会受到一些问题的困扰，如空间假频等.一般来说地震数据在空间方向采样稀疏或不规则，会导致假频问题的出现.黄新武等(2003)详细分析了由于采样不足造成的抛物Radon变换域假频问题，以及变换域成像数据体的能量发散和拉伸情况，Schonewille等(2001)将离散Fourier变换理论映射到抛物Radon域，推导出了能够成功应用抛物Radon变换的采样准则，以及能够稳定求解的曲率采样参数最小间隔.Greenhalgh(1990)和Turner(1990)等人对线性Radon变换中的假频问题做了详细讨论，刘喜武等(2004)从倾斜叠加的概念出发，综合讨论了高分辨率Radon变换的方法及其在地震信号处理中的应用，并给出了求解的具体算法.熊登等(2009)提出了一种混合域高分辨抛物Radon变换压制多次波的方法，既保持了较高的分辨率又有很高的计算效率. Zhou Yu等(2007)提出了一种基于多尺度Wavelet-Radon变换的假频消除方法，并将其应用于地震数据重建方面.牛滨华(2001)介绍了二次多项式Radon变换，讨论了多项式正反Radon变换的公式、实现方法和有关计算参数的选择.薛雅茹等(2012)从保护一次波AVO特性方面提出了一种基于Radon变换和正交多项式变换的多方向正交多项式变换压制多次波方法.冯晅等(2011)依据多道相关中衡量多道信号相似性的能量比标准，对叠加过程加以控制，压制变换中出现的假频. Wang Yanghua(2002)在抛物Radon变换及线性Radon变换的基础上提出了一种时间延迟Radon变换，使用远偏移距道的时间延迟量Γ来代替传统抛物Radon变换中的曲率参数q或线性Radon变换的射线参数p，并推导了Γ的反假频条件.

本文将反假频时延Radon变换应用于多次波压制方面，并利用预条件算子在时延Radon变换前进行处理，可有效避免变换域假频的产生.使用时延Radon变换时，其变换域成像精度的主要影响因素为输入地震数据的道数，而不是传统变换中的空间方向的采样间隔.预条件算子可通过空间方向的重建，进而增加或规则化输入数据的道数，提高变换域成像数据的质量，最终可有效实现多次波压制处理. 1 时延Radon变换基本理论

时延Radon变换利用远偏移距道的时间延迟量Γ代替传统抛物Radon变换中的曲率参数q.实际运算时，Radon 正变换的结果m(τ，q)可通过求解如下表达式的反问题得到，

式中：d(t，x)为时空域的输入数据.该非线性求逆问题的离散形式可通过类比Fourier变换理论表示为

曲率参数q描述了顶点位于零偏移距处的抛物线，而远偏移距道的延迟时间表达式为

Γ的值可较为容易地由地震记录得到，如图 1所示，而q的值则需通过计算(3)式得到.令参数γ=qx2，抛物Radon反变换(2)的形式可改写为

式中：di(ω)为第i道的采样数据，mj(ω)为第j个相干同相轴的子波，γij为第i道的第j个同相轴的时差，式(4)是以延迟时差γij为参数的Radon变换.
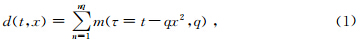
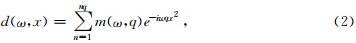
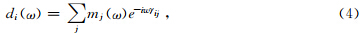
图 1 时延Radon变换中参数Γ示意图Fig. 1 Schematic diagram of parameter Γ in delay time Radon transform

时延Radon变换中，时间方向的采样对变换域的假频影响不大，但是Γ离散化程度的选取则是Radon域数据成像效果的关键因素.

方程(2)的积分形式可表示为

根据Fourier变换形式的Nyquist采样定理，可知由反假频条件得到的参数q采样间隔为

如果将方程(5)视为从m(ω，q)到d(ω，x)的Fourier正变换，那么关于变量x2的反Fourier变换可定义为

根据Fourier变换理论，空间采样的反假频条件为

对于给定的数据体，xmax和Δx为固定值，通过方程(8)可推导出曲率的最大范围

这里假设Δx≡Δxmax，即空间方向为规则采样的情况.

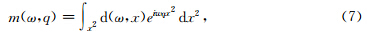
方程(6)和(9)为传统抛物Radon变换的两个反假频条件.若将方程两边同时乘以x2max，则关于远偏移距道的延迟时间Γ的反假频条件可表示为

式中，Μ代表Radon变换输入数据的道数，方程(10)和(11)代表的是关于频率的函数.

抛物Radon变换的反假频条件(9)是关于空间采样间隔和最大偏移距的函数.当使用时延Radon变换时，反假频条件(11)表明参数Γ的范围由输入道集的道数Μ控制.对于固定的最大偏移距xmax来说，增加道数Μ会增大Γlimit.这种情况下，增加道数Μ则会减小采样间隔Δx，进而增大qlimit.对于固定的采样间隔Δx，式(11)表明增加道数Μ会增大Γlimit，同时意味着增大xmax，根据式(9)，qlimit将会减小. 2 预条件反假频算子

就实际地震记录而言，特别是浅层部分，Γ的最大值往往要超过假频条件(11)所定义的Γlimit.在理想情况下，Γ的Radon变换道数应严格依赖于频率.然而当道集的实际Γ值大于反假频限制时，就不能较好地模拟地震数据的同相轴，Radon域成像在高Γ值处会出现分散的背景噪音，即空间假频.为了压制假频，可以设计一个低通滤波器，将其应用于Radon域的成像结果.一般来说，滤波函数为

该滤波器将滤除上式定义的频率范围以外的部分，但是这种反假频处理方法虽然 消除了 假频在 Radon域成像结果的能量，但在Radon反变换后会在远偏移距位置出现误差.本文提出在Radon变换前，利用预条件算子对输入数据进行处理，设计的预条件算子将重建道集至足够的道数.按照反假频条件(11)，Radon变换前至少需要输入的道数为

式中，ω0为参考频率.实际计算时，为了提高计算效率，使用了最大频率ωmax.Μ代表原始数据道数，M*代表预条件处理后数据道数.

定义 Q 为预条件处理算子(M*×M)，将输入的Μ道转化为M*道输出. R *(N×M*)是将重采样的 M *道数据变换为Radon域N道的算子，R(N×M)为将输入的Μ道数据变换为Radon域N道算子.则 R 可表示为

Radon正变换定义为

式中，d代表包含多次波的原始数据向量，m 为Radon域成像结果的向量.Radon反变换的形式由方程(4)给出.

L为M×N的相位变化矩阵.

Radon算子R*的求解方式与方程(16)线性系统的求解方式相似，但是其观测系统不同，输入数据的道数为M*而非Μ，即：

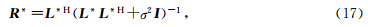
L*为M*×N的相位变化矩阵，L *H为 L *的Hermitian型转置矩阵，σ2为增强求解稳定性的系数，σ2通常取主对角线上数据的1%，I为单位矩阵.

预条件算子Q 由一对正反离散Fourier变换算子构成，

F +代表与输入数据观测系统有关的离散Fourier正变换算子，F *代表离散Fourier反变换算子.

正向离散Fourier变换(DFT)的谱通过求解如下的线性方程得到

d(x)为x坐标轴方向的信号序列，u(kl)为波数谱.Δk为均匀波数采样间隔，kl=lΔk.式(19)的矩阵乘向量形式为

式(18)中的正向DFT算子 F +定义为

式中，C 为稀疏约束矩阵，用于控制DFT谱的稀疏度.式(18)中的反向DFT算子F*与F 的定义方式相同，只不过空间采样不同.

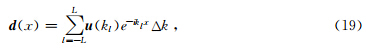
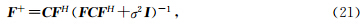
预条件算子通过增加输入数据的道数可以大大降低Radon域的假频噪音.这种时延Radon变换可应用于任意形式的积分路径，既可模拟抛物Radon变换也可模拟线性Radon变换.预条件算子矩阵 Q 只与输入数据的观测系统有关，而与频率无关，因此对每个输入道集只需要计算一次，便可应用于所有频率成分.另外为改善计算效率，在实际运算时引入了GPU技术加速矩阵运算.输入数据既可以是空间规则采样也可以是非规则采样，对于不规则采样的Μ道数据体来说，其Nyquist波数是由各采样点间的平均采样间隔决定的.即可覆盖的最大空间波数为

Δxa为不规则数据体的平均空间采样间隔.

在利用预条件算子克服假频问题的同时，也在Radon变换之前也起到了空间规则化的作用.通常在Radon变换计算中，需要对每个输入道集的观测系统进行检查，判断其Radon算子是否需要重新计算.由于预条件算子对每个道集做了规则化，矩阵R*只需对拥有M *道的观测系统进行计算即可应用于整条测线.假设某一道集的观测系统与其它道集不同，预条件算子只需重新计算一次，因为它与频率无关.但是如果Radon变换的算子重新计算，由于Radon算子与频率有关，则所有频率的最小平方解都需要重新计算，也就是说在Radon变换前利用预条件算子进行处理可提高整体计算效率. 3 算例分析 3.1 水平层状介质模型

按照上述理论，形成了反假频的时延Radon变换方法，为验证方法的正确性，首先设计简单层状介质模型进行方法实验.理论合成的单炮地震记录共1000个采样点，时间采样间隔为4 ms，模拟数据的地震子波为主频25 Hz的Ricker 子波，单炮包括400道数据，原始记录空间采样间距为20 m，在实际计算时将炮记录抽稀，每3道保留1道，即单炮数据为134道，道间距为60 m.模型共包括5个水平地层，介质速 度由上至下分别为2500 m/s、2000 m/s、3200 m/s、3000 m/s、 2000 m/s，密度为给定的恒定值，2.4 g/cm3，每层层厚均为400 m.

图 2a为模拟的含多次波原始炮记录，除四个有效波同相轴外，还包括复杂的多次波噪音干扰，图 2b为经部分NMO校正后的炮记录，该记录传统时延Radon变换结果如图 2c所示，由于空间方向采样稀疏，在图 2c中出现了较为明显的假频噪音.应用本文提出的预条件反假频算子进行处理，结果如图 2d所示，假频得到了有效压制，对图 2d的结果在Radon域进行多次波压制的滤波处理，滤波后的结果如图 2e所示，最后将该结果进行时延Radon反变换，即得到时间空间域多次波压制后的炮记录，如图 2f所示.分析可知应用该方法压制多次波后，四个有效波同相轴能量都得到很好的保持，也就是说该方法在压制规则噪音、提高地震数据信噪比的同时，也具有较好的保幅性.

图 2 反假频时延Radon变换多次波压制
(a)原始单炮记录；(b)部分NMO后炮记录； (c)传统时延Radon域剖面； (d)预条件算子反假频Radon域剖面；(e)滤波后的结果；(f)多次波压制结果.Fig. 2 Multiple suppression by anti-alias delay time Radon transform approach
(a)Original shot record;(b)Shot record after NMO correction; (c)Conventional time delay Radon domain panel; (d)Radon domain panel after pre-condition processing;(e)Radon panel after filtering; (f)Shot record after multiple suppression.
3.2 复杂地质模型

为测试研制的多次波算法对复杂介质和复杂水域采集资料的适应能力，模拟了复杂地质条件的深海地震数据，其速度模型如图 3所示，该模型的海底条件复杂，同时也包括复杂断层和尖灭等地质现象.对该模型应用单程波动方程方法完成了理论数据模拟，模拟炮记录的时间采样间隔为2 ms，道长为2 s，也就是1000个时间采样点，正演模拟了800炮合成地震记录，每炮400道，道间距为10 m.为验证本文给出方法的有效性和实用性，将模拟数据抽稀，抽稀后的炮数据的空间采样间隔为30 m.抽稀处理后的第200炮记录如图 4a所示，可以看出深部复杂的多次波现象，以及复杂介质中炮记录同相轴的复杂时距曲线.利用反假频时延Radon变换进行多次波压制计算，多次波压制后的炮记录如图 4b所示.对比两图，可知双程旅行时在1 s以下的不同阶数的多次波均得到较为明显的压制，地震数据的信噪比得到有效提高.

图 3 复杂介质速度模型Fig. 3 Velocity model of complex media

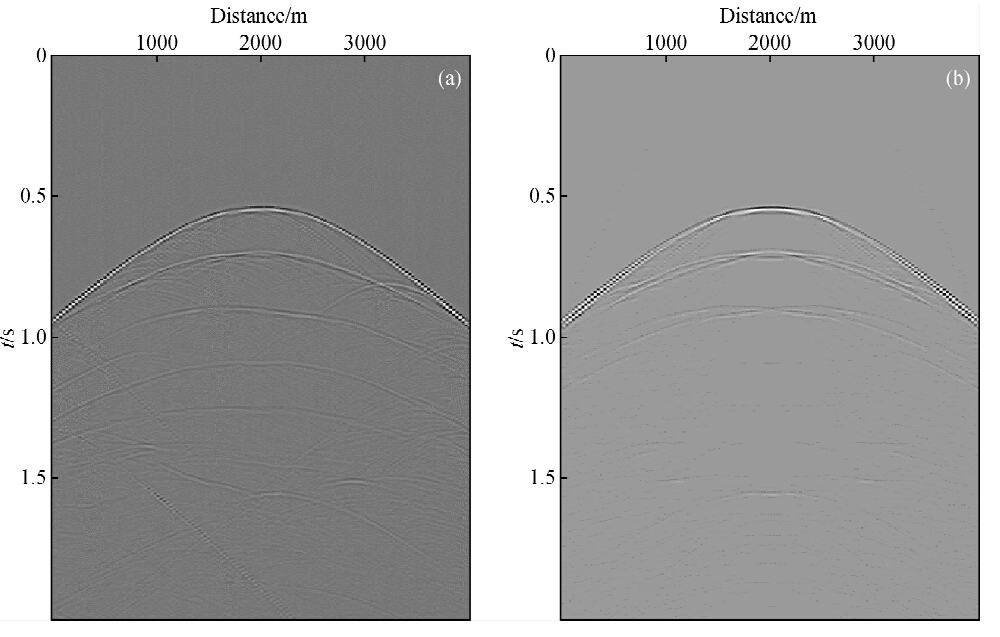图 4 反假频时延Radon变换压制复杂模型数据的多次波
(a)含多次波的原始炮记录；(b)反假频时延Radon变换多次波压制结果. Fig. 4 Multiple suppression in complex synthetic data by anti-alias delay time Radon transform approach
(a)Original shot record with multiples;(b)Multiple suppression result by delay time Radon transform approach.
4 结 论

利用Radon变换方法压制多次波，通过引入时间延迟量Γ，输入数据的道数就成为直接影响Radon域假频的重要参数.利用预条件算子对数据的空间采样方向重新采样或规则化处理，可消除时延Radon变换域中空间假频的影响，提高Radon变换域数据成像的精度.为进一步提高计算效率，在计算时延Radon变换过程中，引入GPU/CPU协同并行加速计算技术，以减小地震数据多次波预处理的周期.理论模型数据的试算进一步表明，反假频时延Radon变换压制多次波方法，可有效压制地震数据中的多次波，也可有效保持地震数据中有效波的振幅.

参考文献
[1] Binzhong Zhou, Stewart A. Greenhalgh. 1994. Wave-equation extrapolation-based multiple suppression: 2-D filtering in the f-k domain[J]. Geophysics, 59(9): 1377-1391.
[2] Binzhong Zhou, Stewart A. Greenhalgh. 1996. Multiple suppression by 2D filtering in the parabolic τ-pdomain: a wave-equation -based method[J]. Geophysical Prospecting, 44: 375-401.
[3] Charles I. Puryear, Oleg N. Portniaguine, Carlos M. Cobos, et al. 2012. Constrained least-squares spectral analysis: Application to seismic data[J]. Geophysics, 77(5): 143-167.
[4] Daniel Trad, Tadeusz Ulrych, Mauricio Sacchi. 2003. Latest views of the sparse Radon transform[J]. Geophysics, 68(1): 386-399.
[5] Douglas J. Foster, Charles C. Mosher. 1992. Suppression of multiple reflections using the Radon transform[J]. Geophysics, 57(3): 386-395.
[6] Einar Maeland. 2003. Short Note Disruption of seismic images by the parabolic Radon transform[J]. Geophysics, 68(3): 1060-1064.
[7] Ethan J. Nowak, Matthias G. Imhof. 2006. Amplitude preservation of Radon-based multiple-removal filters[J]. Geophysics, 71(5): 123-126.
[8] Feng X, Zhang X W, Liu C, et al. 2011. Separating P-P and P-SV wave by parabolic Radon transform with multiple coherence. Chinese J. Geophys., 54(2): 304-309. doi: 10.3969/j.issn.0001-5733.2011.02.005.
[9] Greenhalgh S.A., Mason I.M., Lucas E., et al. 1990. Controlled direct ion reception filtering of P- and S- waves in τ-pspace[J]. Geophysical Journal International, 100: 221-234.
[10] Huang X W, Wu L, Niu B H, et al. 2003. Sampling and aliasing of parameters in parabolic Radon transform[J]. Journal of the University of Petroleum,China, 27(2): 27-31.
[11] Kabir M N, Verschuur D J. 1995. Restoration of missing offsets by parabolic Radon transform[J]. Geophysical Prospecting, 43: 347-368.
[12] Kurt J. Marfurt, Robert V. Schneider, Michael C. Mueller. 1996. Pitfalls of using conventional and discrete Radon transforms on poorly sampled data[J]. Geophysics, 61(5): 1467-1482.
[13] Li X, Hu T Y. 2009. Surface-related multiple removal with inverse scattering series method[J]. Chinese J. Geophys., 52(6): 1633-1640. doi: 10.3969/j.issn.0001-5733.2009.06.026.
[14] Li Z C, Li Z N, Guo S J, et al. 2013. Comparison of multiple attenuation methods in data domain and image domain[J]. Progress in Geophysics, 28(6): 2901-2910. doi:10.6038/pg20130610.
[15] Liu X W, Liu H, Li Y M. 2004. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 19(1): 8-15.
[16] Liu Y K, Zhu W L, Mi L J, et al. 2014. Characteristics of multiples in the slope of the northern South China Seaand the suppressing method[J]. Chinese J. Geophys., 57(10): 3354-3362. doi: 10.6038/cjg20141022.
[17] Ma J T, Mrinal K. Sen, Chen X H. 2009. Multiple attenuation using inverse data processing in the plane-wave domain[J]. Chinese Journal Geophysics, 52(3): 808-816.
[18] Turner G. 1990. Aliasing in the τ-p transform domain and the removal of spatial aliased coherent noise[J]. Geophysics, 55: 1496-1503.
[19] Wang B L, M. D. Sacchi, Ying X Y, et al. 2014. Multiple attenuation based on amplitude preserving Radon transform[J]. Chinese J. Geophys., 57(6): 1924-1933, doi: 10.6038/cjg20140623.
[20] Wang Yanghua. 2002. Antialiasing conditions in the delay-time Radon transform[J]. Geophysical prospecting, 50: 665-672.
[21] Wang Yanghua. 2003. Sparseness-constrained least-squares inversion:Application to seismic wave reconstruction[J]. Geophysical prospecting, 51: 75-87.
[22] Wang Yanghua. 2003. Multiple suppression: coping with the spatial truncation effect in the Radon transform domain[J]. Geophysical prospecting, 50: 665-672.
[23] Schonewille M A, Duijndam A J W. 2001. Parabolic Radon transform,sampling and efficiency[J]. Geophysics, 66(2): 667-678.
[24] Song J W, D.J. Verschuur, Chen X H. 2014. Research status and progress in multiple elimination[J]. Progress in Geophysics, 29(1): 240-247, doi:10.6038/pg20140134.
[25] Wenkai Lu. 2013. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 78(4): 147-155.
[26] Xiong D, Zhao W, Zhang J F. 2009. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese J. Geophys., 52(4): 1068-1077, doi: 10.3969/j.issn.0001-5733.2009.04.024.
[27] Xue Y R, Chen X H, Ma J T. 2012. Multiples attenuation based on directional orthogonal polynomial transform[J]. Chinese J. Geophys., 55(10): 3450-3458, doi: 10.6038/j.issn.0001-5733.2012.10.028.
[28] Zhou Yu, John Ferguson, George McMechan, Phil Anno. 2007. Wavelet-Radon domain dealiasing and interpolation of seismic data[J]. Geophysics, 72(2): 41-49.
[29] Zhu S W, Wei X C, Li F, et al. 2002. Separating and suppressing multipies by sparse solution of parabolic Radon transform[J]. Oil Geophysical prospecting, 37(2): 110-115.
[30] 薛亚茹, 陈小宏, 马继涛. 2012. 多方向正交多项式变换压制多次波[J]. 地球物理学报, 55(10): 3450-3458, doi:10.6038/j.issn.0001-5733.2012.10.028.
[31] 冯晅, 张先武, 刘财, 等. 2011. 带有多道相关的抛物线Radon变换法分离P-P、P-SV波[J]. 地球物理学报, 54(2): 304-309, doi:10.3969/j.issn.0001-5733.2011.02.005.
[32] 马继涛, Mrinal K. Sen, 陈小宏. 2009. 平面波域反数据处理压制多次波方法研究[J]. 地球物理学报, 52(3): 808-816.
[33] 熊登, 赵伟, 张剑锋. 2009. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 52(4): 1068-107. doi:10.3969/j.issn.0001-5733.2009.04.024.
[34] 李翔, 胡天跃. 2009. 逆散射级数法去除自由表面多次波[J]. 地球物理学报, 52(6): 1633-1640, doi:10.3969/j.issn.0001-5733.2009.06.026.
[35] 王保丽, M. D. Sacchi, 印兴耀, 等. 2014. 基于保幅拉东变换的多次波衰减[J]. 地球物理学报, 57(6): 1924-1933, doi:10.6038/cjg20140623.
[36] 刘伊克, 朱伟林, 米立军, 等. 2014. 南海北部陆坡区多次波发育特征及压制策略分析[J]. 地球物理学报, 57(10): 3354-3362, doi:10.6038/cjg20141022.
[37] 刘喜武, 刘洪, 李幼铭. 2004. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 19(1): 8-15.
[38] 宋家文, D.J.Verschuur, 陈小宏. 2014. 多次波压制的研究现状与进展[J]. 地球物理学进展, 29(1): 240-247, doi:10.6038/pg20140134.
[39] 李振春, 李志娜, 郭书娟, 等. 2013. 数据域与成像域多次波压制方法对比[J]. 地球物理学进展, 28(6): 2901-2910, doi:10.6038/pg20130610.
[40] 黄新武, 吴律, 牛滨华, 等. 2003. 抛物线Radon变换中的参数采样与假频[J]. 石油大学学报, 27(2): 27-31.
[41] 朱生旺, 魏修成, 李锋, 等. 2002. 用抛物线Radon 变换稀疏解分离和压制多次波[J]. 石油地球物理勘探, 37 ( 2 ): 110-115.