2. 成都地质调查中心, 成都 610082;
3. 东华理工大学 核工程与地球物理学院, 南昌 344000
2. Chengdu Center, China Geological Survey, VChengdu, Sichuan 610082, China;
3. College of Nuclear Engineering and geophysics, ECIT, Nanchang, Jiangxi 344000, China
随着地球物理勘探事业的发展,复杂地区的勘探日益增多,野外干扰因素也进一步加大,瞬变电磁法数据采集越来越受工作区域条件的限制,特别是在隧道、井下超前探中,由于施工条件有限,只能采取多匝小线框装置(于景邨等,2007;岳建华等,2007;杨海燕和岳建华2008).在金属矿山及很多领域的勘探中需要以深部勘探为目的的瞬变电磁测深则需要大线框装置(张保祥和刘春华,2004;薛国强等,2011;侯彦威,2012;陈卫营和薛国强,2013).
笔者在使用一些商用软件处理瞬变电磁资料的过程中发现:多数软件对100 m×100 m重叠回线、中心装置采集的数据反演拟合曲线及反演效果较好.对于多匝小线框装置的反演曲线与实测曲线的拟合不太理想,且电阻率变化剧烈,反演电阻率较实际情况偏小.对于边长超过100 m×100 m的装置特别是内(中心)回线装置,反演曲线与实测曲线的拟合也不是很好,甚至出现不能反演的情况,反演电阻率也较实际情况偏高.要解决这个问题需要更高维数的反演软件(2D、3D).近年我国高维瞬变电磁正演技术发展迅速,出现了2维、2.5维、3维正演(熊彬和罗延钟,2004;岳建华等,2007;杨海燕和岳建华,2008;李建慧等,2013;薛国强等,2014).但以上方法还停留在正演阶段,目前瞬变电磁法商用 反演的软件虽然种类繁多,但资料处理解释水平不高,基本停留在一维阶段(薛国强等,2008).为克服该困难,本文针对瞬变电磁法1D反演,通过物理模拟准则推导出相同模型的发射线框边长非100 m的回线装置与发射边长100 m重叠回线装置响应转换公式,将小线框重叠回线、内(中心)回线,大线框内(中心)回线、重叠回线响应转化为100 m×100 m发射线框的重叠回线,然后进行反演.该方法定名为物理模拟相似法(Physical Simulation Method).通过该方法预处理后的反演结果与不做预处理反演结果对比,判断预处理方法的有效性. 1 相似准则
实验室中模拟自然界的某种物理现象所遵守的一定的准则,在物理模拟中称之为相似准则.电磁法的物理模拟所遵守的相似准则,从麦克斯韦方程推出,基本的有两条.同时遵守着两条准则进行模拟实验,称之为全模拟.对于时间域电磁法,这两条准则

由于位移电流在绝大多数情况下都可忽略不计,即介电常数的影响很小,所以几乎所有的模拟实验工作都可以不考虑(1)式的准则.由于时间域电磁法测量的是绝对量,是有量纲的,所以除需模拟场的几何分布形态外,尚需模拟系统的绝对值,这样的模拟除也常简称为几何模拟外,有时又称之为绝对(比例)模拟,绝对模拟需附加一个条件:

此式称为振幅校正系数.
应当指出(3)式是在假设电流相同,采用重叠回线或同一回线组合,并且都只有一匝回线的情况下得出的,如果野外工作与模拟实验的电流不相等,圈数又不同,或者是采用中心回线组合,对于重叠回线组合应遵守


对(1)式做进一步分析,需进一步说明的是: 在介质只导电而不导磁的情况下,即μm=μf,则(1)式简化为

(蒋邦远,1998). 2 预处理方法
由于很多反演软件对100 m×100 m的发射线框反演效果较好,因此取Lf=100 m,不管重叠、同一、中心回线装置均取AR=10000 m2.
因此假设取tm=tf,由(6)式得


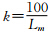 ,则有
,则有


均匀半空间中心回线、重叠回线、同一回线的晚期近区电阻率计算公式为
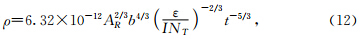

令和为归一化感应电位(即I=1 A),有

采用 对非100 m×100 m单匝重叠回线的重叠、内(中心)回线装置进行延时和感应电位的转换,即可得到相同地电模型下的100 m×100 m单匝重叠回线的响应曲线.其处理流程参见图 1:
对非100 m×100 m单匝重叠回线的重叠、内(中心)回线装置进行延时和感应电位的转换,即可得到相同地电模型下的100 m×100 m单匝重叠回线的响应曲线.其处理流程参见图 1:
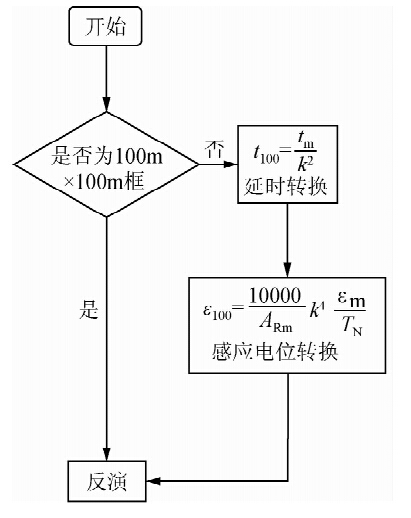 | 图 1 处理方法流程图Fig. 1 The process of this method |
本文选取一个边长小于100 m发射线框例子和两个边长大于100 m发射线框例子,分别从一维反演模型响应曲线与实测曲线的拟合程度,反演电阻率与实际电阻率的接近程度,以及反演结果与实际地质情况的接近程度来说明相似模拟法应用在瞬变电磁法反演前预处理的有效性. 3.1 10 m×10 m重叠回线装置
例1的装置为10 m×10 m多匝重叠回线装置,装置为正方形框,边长10 m,发射线框为4匝,接收线框为4匝,测点间距为20 m.从单点数据实测曲线和一维反演模型响应曲线来看(图 2),未经预处理的测量数据和反演模型响应曲线拟合度不高,特别是在曲线的后期数据(实测数据曲线和反演模型响应曲线RMS=2.605).预处理后的反演模型的响应曲线几乎与实测曲线重合(实测数据曲线和反演模型响应曲线RMS=0.103).显然,单从实测曲线与反演模型响应曲线拟合度来看,预处理后的曲线拟合度大大提高.从反演电阻率拟断面图(图 3、4)可以看出,预处理前和预处理后的断面图大致趋势一致,但低阻异常中心深度存在一定差异.从反演电阻率看,采用原始数据的反演电阻率值从0.1~90 Ω · m,断面图中电阻率大部分在10 Ω · m以下,明显比实际的电阻率偏低.经预处理后的反演电阻率值从5~200 Ω · m断面图中反演电阻率大部分高于50 Ω · m,比未经预处理的反演电阻率更接近实际情况.从矿方提供的钻孔 验证资料来看,煤层采空区底板在约60 m深度处,且采空区塌陷充水,显然采用该方法预处理后的低阻异常体深度更接近实际情况,反演电阻率也更接近实际的电阻率值.由此可见相似模拟法对于瞬变电磁多匝小线框在反演前的预处理是有效的.
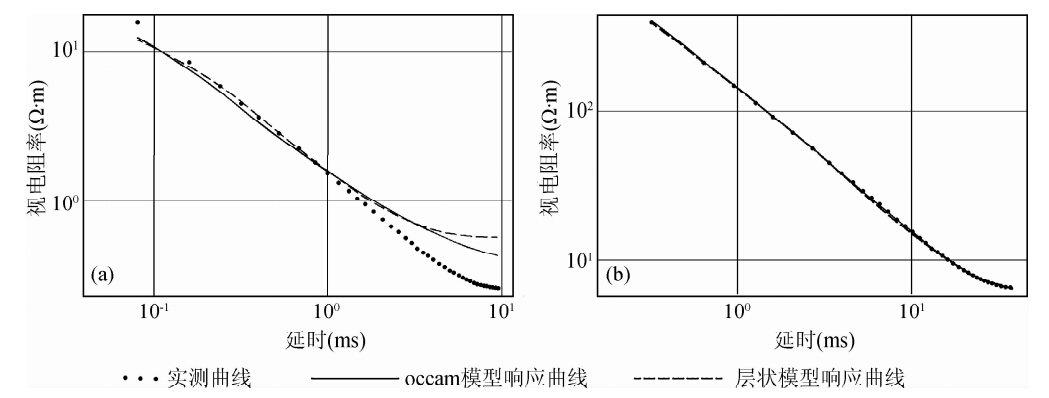 | 图 2 10 m×10 m多匝小回线重叠回线装置拟合情况预处理前后对比图Fig. 2 The fitting situation diagram of the 10 m×10 m coincident loop configuration before and after preprocessing |
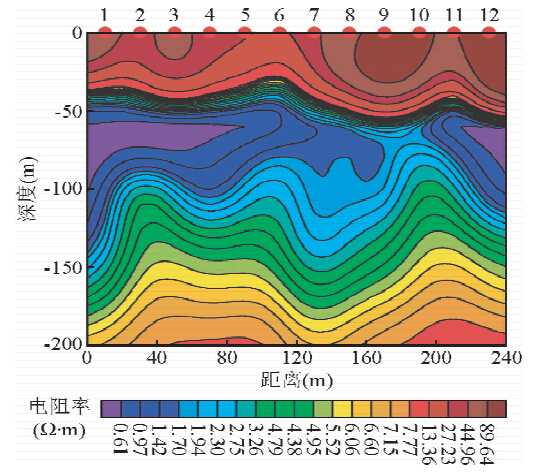 | 图 3 10 m×10 m多匝小回线重叠回线装置反演结果Fig. 3 The inversion results of the 10 m×10 m coincident loop configuration |
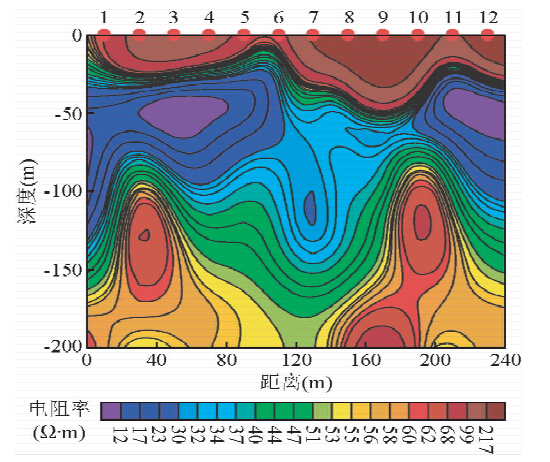 | 图 4 预处理后反演结果Fig. 4 The inversion results after preprocessing |
例2的装置为200 m×200 m中心回线装置,装置为正方形框,边长200 m,发射线框为1匝,接收线框为2m×2m×100匝,测点间距为20 m.该装置采集的原始数据采用几种商用反演软件均不能得到反演结果,而采用物理模拟相似法将实测数据转化为100 m×100 m重叠回线装置的响应可以得到反演结果(见图 5).该数据采集地点地表为含水土层,地表部分出露泥质板岩,从钻孔资料上得知深度10 m到218 m为泥质板岩,在深约218 m处见一层炭质板岩. 从反演电阻率来看,反演电 阻率从 10~500 Ω · m比较接近实际地质情况.这说明相似模拟法对于超过100 m发射线框的中 心回线装置的预处理也是有效的,模拟为100 m×100 m重叠回线装置后的响应数据后的反演结果较接近实际地质情况.
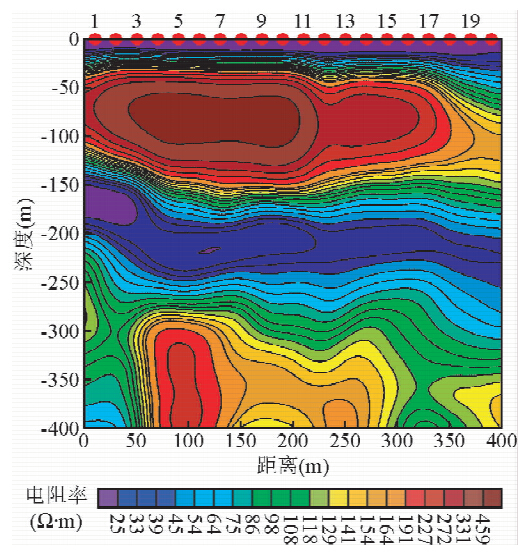 | 图 5 预处理后反演结果Fig. 5 The inversion results after preprocessing |
例3的装置为400 m×600 m定源回线装置,装置发射线框为400 m×600 m单匝矩形线框,接收线框为等效面积200 m2探头,测点间距为25m或50 m.从单点数据实测曲线和一维反演模型响应曲线来看(图 6),未经预处理的测量数据和反演模型响应曲线拟合度不高,特别是在曲线的早期数据(实测数据曲线和反演模型响应曲线RMS=0.851).预处理后的反演模型的响应曲线几乎与实测曲线重合(实测数据曲线和反演模型响应曲线RMS=0.120).显然,单从实测曲线与反演模型响应曲线拟合度来看,预处理后的曲线拟合度有所提高.从反演电阻率拟断面图(图 7、8)可以看出,预处理前和预处理后的断面图大致趋势一致,但浅部异常的形态和位置有所差异.从反演电阻率看,采用原始数据的反演电阻率值从500~15000 Ω · m,断面图中电阻率大部分在4000 Ω · m以上,明显比实际的电阻率偏高.经预处理后的反演电阻率值从80~1200 Ω · m,比未经预处理的反演电阻率更接近实际情况.从分辨率来看,预处理后的反演断面图在横向上,特别是浅部更高.从矿方提供的已知资料来看,在2号测点附近,和12号测点附近为已知的铅锌矿体,预处理前的反演结果12号点附近的矿脉有低阻反应,而2号点附近则没有异常,而预处理后的断面图两条矿脉均有反应,因此相似模拟法对于大定源内测装置也具有一定效果.
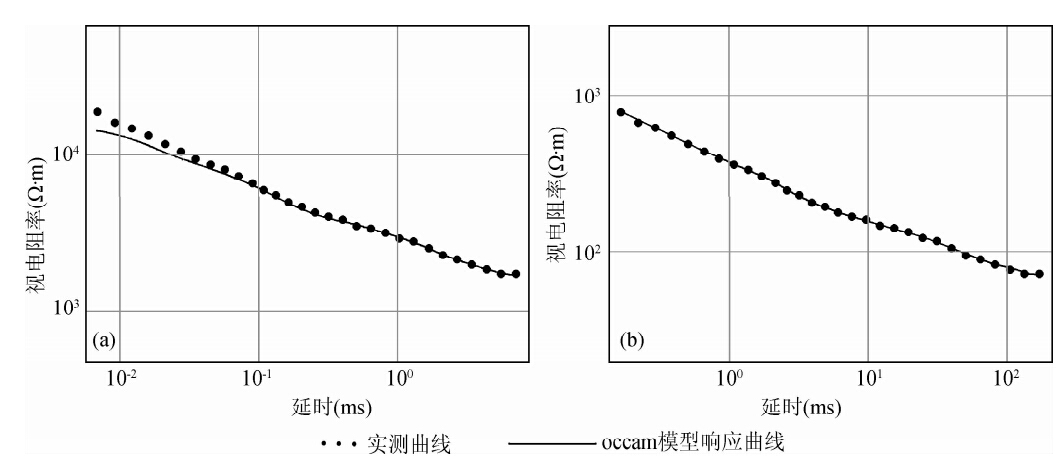 | 图 6 400 m×600 m定源回线装置拟合情况预处理前后对比图Fig. 6 The fitting situation diagram of the 400 m×600 m fixed loop configuration before and after preprocessing |
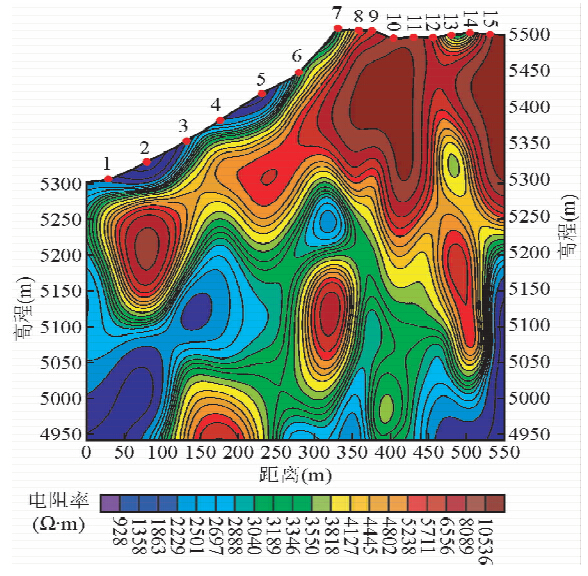 | 图 7 400 m×600 m定源回线装置反演结果Fig. 7 The inversion results of the 400 m×600 m fixed loop configuration |
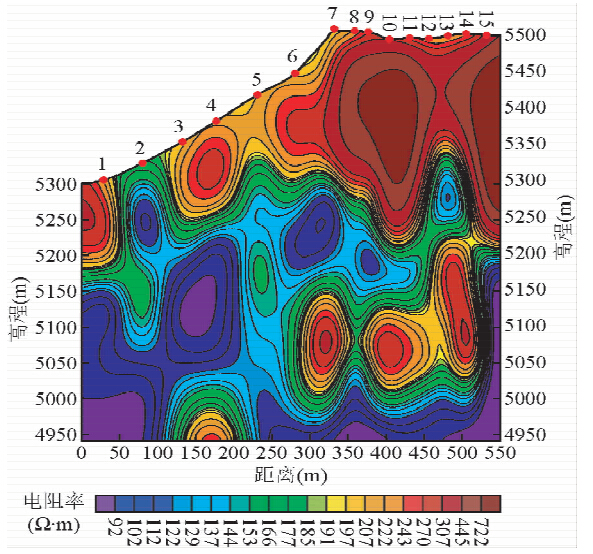 | 图 8 预处理后反演结果Fig. 8 The inversion results after preprocessing |
| [1] | Chen S D, He S, Zhang S. 2014. Calibration of ground transient electromagnetic system[J]. Progress in Geophysics (in Chinese), 29(2): 660-667, doi:10.6038/pg20140225. |
| [2] | Chen W Y, Xue G Q. 2013. Application on coal-mine voids detection with multi-device TEM technology[J]. Progress in Geophysics (in Chinese), 28(5): 2709-2717, doi:10.6038/pg20130554. |
| [3] | Cheng J L, Li M X, Xiao Y L, et al. 2014. Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space[J]. Chinese Journal of Geophysics (in Chinese), 57(10): 3478-3484, doi:10.6038/cjg20141033. |
| [4] | Dai Q W, Hou Z C, Chai X C. 2013. Application of transient electromagnetic method and EH-4 to investigation of mined-out areas of molybdenum deposits[J]. Progress in Geophysics (in Chinese), 28(3): 1541-1546, doi:10.6038/pg20130350. |
| [5] | Ding Y F, Bai D H, Xu C. 2012. A rapid algorithm for calculating time domain transient electromagnetic responses of a large fixed rectangular loop on the half space[J]. Chinese Journal of Geophysics (in Chinese), 55(6): 2087-2096, doi:10.6038/j.issn.0001-5733.2012.06.030. |
| [6] | Fang W Z, Li Y G, Li X. 1993. Transient Electromagnetic Sounding Method Principle (in Chinese) [M]. Xi'an: Northwestern University Press, 9-15. |
| [7] | Hou Y W. 2012. The detection on the using of transient electromagnetic method search for deep water source in Inner Mongolia[J]. Progress in Geophysics (in Chinese), 27(6): 2698-2703, doi:10.6038/j.issn.1004-2903.2012.06.049. |
| [8] | Jiang B Y. 1998. People's Republic of China Ministry of Geology and Mineral Resources (in Chinese) [M]. Beijing: Geological Publishing House, 162-198. |
| [9] | Kaufman A A, Keller G V. 1987. Frequency and Transient Soundings (in Chinese) [M]. Wang J M Translate. Beijing: Ecological Publishing House, 246-281. |
| [10] | Li J H, Hu X Y, Zeng S H, et al. 2013. Three-dimensional forward calculation for loop source transient electromagnetic method based on electric field Helmholtz equation[J]. Chinese J. Geophys. (in Chinese), 56(12): 4256-4267, doi:10.6038/cjg20131228. |
| [11] | Li J H, Zhu Z Q, Zeng S H, et al. 2012. Progress of forward computation in transient electromagnetic method[J]. Progress in Geophys. (in Chinese), 27(4): 1393-1400, doi:10.6038/j.issn.1004-2903.2012.04.013. |
| [12] | Li J H, Zhu Z Q, Lu G Y, et al. 2013. Study on three-dimensional forward of transient electromagnetic method excited by loop source[J]. Progress in Geophys. (in Chinese), 28(2): 754-765, doi:10.6038/pg20130224. |
| [13] | Li X. 2002. Transient Electromagnetic Sounding Theory and Its Application (in Chinese) [M]. Xi'an: Shanxi Science and Technology Press, 9, 1-4, 102-105. |
| [14] | Niu Z L. 2007. Transient Electromagnetic Theory (in Chinese) [M]. Changsha: Central South University Press, 12, 64-65. |
| [15] | Piao H R. 1990. Principle of Electromagnetic Sounding Method (in Chinese) [M]. Beijing: Geological Publishing House, 139-161. |
| [16] | Qiu Z P, Li Z H, Li D Z, et al. 2013. Non-orthogonal-Grid-based three dimensional modeling of transient electromagnetic field with topography[J]. Chinese Journal of Geophysics (in Chinese), 56(12): 4245-4255, doi:10.6038/cjg20131227. |
| [17] | Xin H C, Tang J T, Xu Z M. 2014. Finite-difference modeling of 2.5-D transient electromagnetic[J]. Progress in Geophysics (in Chinese), 29(5): 2278-2286, doi:10.6038/pg20140543. |
| [18] | Xiong B, Luo Y Z. 2006. Finite element modeling of 2.5-D TEM with block homogeneous conductivity[J]. Chinese J. Geophys. (in Chinese), 49(2): 590-597, doi:10.3321/j.issn:0001-5733.2006.02.036. |
| [19] | Xue G Q, Li X, Di Q Y. 2007. The progress of TEM in theory and application[J]. Progress in Geophysics (in Chinese), 22(4): 1195-1200, doi:10.3969/j.issn.1004-2903.2007.04.026. |
| [20] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
| [21] | Xue G Q, Qin K Z, Li X, et al. 2011. Discovery and TEM detection to a large-scale porphyry molybdenum deposit in Tibet[J]. Progress of Geophysics (in Chinese), 26(3): 954-960, doi:10.3969/j.issn.1004-2903.2011.03.022. |
| [22] | Xue G Q, Chen W Y, Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding[J]. Chinese Journal of Geophysics (in Chinese), 56(1): 255-261, doi:10.6038/cjg20130126. |
| [23] | Xue G Q, Wang H Y, Yan S, et al. 2014. Time—domain Green function solution for transient electromagnetic field[J]. Chinese J. Geophys. (in Chinese), 57(2): 671-678, doi:10.6038/cjg20140230. |
| [24] | Yan S, Chen M S, Fu J M. 2002. Direct time-domain numerical analysis of transient electromagnetic fields[J]. Chinese J. Geophys. (in Chinese), 45(2): 275-284. |
| [25] | Yang H Y, Yue J H. 2008. Response characteristics of the 3D whole-space TEM disturbed by roadway[J]. Journal of Jilin University (Earth Science Edition) (in Chinese), 38(1): 129-134. |
| [26] | Yang J M, Wei Z Z, Gao X W. 2014. The application of the methods of high density resistivity method and transient electromagnetic to detecting coal mining Goaf and to inspect grouting effect[J]. Progress in Geophysics (in Chinese), 29(1): 362-369, doi:10.6038/pg20140151. |
| [27] | Yu J C, Liu Z X, Tang J Y, et al. 2007. Transient electromagnetic detecting technique for water hazard to the roof of fully mechanized sub-level caving face[J]. Journal of China University of Mining and Technology (in Chinese), 36(4): 542-546. |
| [28] | Yue J H, Yang H Y, Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine [J]. Progress in Geophysics (in Chinese), 22(6): 1904-1909, doi:10.3969/j.issn.1004-2903.2007.06.036. |
| [29] | Zhang B X, Liu C H. 2004. Summarization on applications to groundwater exploration by using transient electromagnetic methods[J]. Progress in Geophysics (in Chinese), 19⑶: 537-541, doi:10.3969/j.issn.1004-2903.2004.03.008. |
| [30] | Zhang S, He S, Chen S D. 2014. Effect of high-order mutual induction response on transient electromagnetic system calibration[J]. Progress in Geophysics (in Chinese), 29(1): 191-196, doi:10.6038/pg20140126. |
| [31] | 陈曙东, 何胜, 张爽. 2014. 地面瞬变电磁系统标定的理论研究[J]. 地球物理学进展, 29(2): 660-667, doi:10.6038/pg20140225. |
| [32] | 陈卫营, 薛国强. 2013. 瞬变电磁法多装置探测技术在煤矿采空区调查中的应用[J]. 地球物理学进展, 28(5): 2709-2717, doi:10.6038/pg20130554. |
| [33] | 程久龙, 李明星, 肖艳丽,等. 2014.全空间条件下矿井瞬变电磁法粒子群优化反演研究[J]. 地球物理学报, 57(10): 3478-3484, doi:10.6038/cjg20141033. |
| [34] | 戴前伟, 侯智超, 柴新朝. 2013. 瞬变电磁法及EH-4在钼矿采空区探测中的应用[J]. 地球物理学进展, 28(3): 1541-1546, doi:10.6038/pg20130350. |
| [35] | 丁艳飞, 白登海, 许诚. 2012. 均匀半空间表面大定源瞬变电磁响应的快速算法[J]. 地球物理学报, 55(6): 2087-2096, doi:10.6038/j.issn.0001-5733.2012.06.030. |
| [36] | 方文藻, 李予国, 李貅. 1993. 瞬变电磁测深法原理[M]. 西安: 西北工业大学出版社, 9-15. |
| [37] | 侯彦威. 2012. 内蒙古地区深部水源瞬变电磁法探测[J]. 地球物理学进展, 27(6): 2698-2703, doi:10.6038/j.issn.1004-2903.2012.06.049. |
| [38] | 蒋邦远. 1998. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 162-198. |
| [39] | 考夫曼, 凯勒. 1987. 频率域和时间域电磁测深[M]. 王建谋译. 北京: 地质出版社, 246-281. |
| [40] | 李建慧, 朱自强, 曾思红,等. 2012. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 27(4): 1393-1400, doi:10.6038/j.issn.1004-2903.2012.04.013. |
| [41] | 李建慧, 朱自强, 鲁光银,等. 2013a. 回线源瞬变电磁法的三维正演研究[J]. 地球物理学进展, 28(2): 754-765, doi:10.6038/pg20130224. |
| [42] | 李建慧, 胡祥云, 曾思红,等. 2013b. 基于电场Helmholtz方程的回线源瞬变电磁法三维正演[J]. 地球物理学报, 56(12): 4256-4267, doi:10.6038/cjg20131228. |
| [43] | 李貅. 2002. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社, 9, 1-4, 102-105. |
| [44] | 牛之琏. 2007. 时间域电磁法原理[M]. 长沙: 中南大学出版社, 12, 64-65. |
| [45] | 朴化荣. 1990. 电磁测深法原理[M]. 北京: 地质出版社, 139-161. |
| [46] | 邱稚鹏, 李展辉, 李墩柱,等. 2013. 基于非正交网格的带地形三维瞬变电磁场模拟[J]. 地球物理学报, 56(12): 4245-4255, doi:10.6038/cjg20131227. |
| [47] | 辛会翠, 汤井田, 徐志敏. 2014. 瞬变电磁法2.5维有限差分正演模拟[J]. 地球物理学进展, 29(5): 2278-2286, doi:10.6038/pg20140543. |
| [48] | 熊彬, 罗延钟. 2006. 电导率分块均匀的瞬变电磁2.5维有限元数值模拟[J]. 地球物理学报, 49(2): 590-597, doi:10.3321/j.issn:0001-5733.2006.02.036. |
| [49] | 薛国强, 李貅, 底青云. 2007. 瞬变电磁法理论与应用研究进展[J]. 地球物理学进展, 22(4): 1195-1200, doi:10.3969/j.issn.1004-2903.2007.04.026. |
| [50] | 薛国强, 李貅, 底青云. 2008. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 23(4): 1165-1172. |
| [51] | 薛国强, 秦克章, 李貅,等. 2011. 西藏沙让特大型钼矿的发现与瞬变电磁法探查[J]. 地球物理学进展, 26(3): 954-960, doi:10.3969/j.issn.1004-2903.2011.03.022. |
| [52] | 薛国强, 陈卫营, 周楠楠,等. 2013. 接地源瞬变电磁短偏移深部探测技术[J]. 地球物理学报, 56(1): 255-261, doi:10.6038/cjg20130126. |
| [53] | 薛国强, 王贺元, 闫述,等. 2014. 瞬变电磁场时域格林函数解[J]. 地球物理学报, 57(2): 671-678, doi:10.6038/cjg20140230. |
| [54] | 闫述, 陈明生, 傅君眉. 2002. 瞬变电磁场的直接时域数值分析. 地球物理学报, 45(2): 275-284. |
| [55] | 杨海燕, 岳建华. 2008. 巷道影响下三维全空间瞬变电磁法响应特征[J]. 吉林大学学报, 38(1): 129-134. |
| [56] | 杨镜明, 魏周政, 高晓伟. 2014. 高密度电阻率法和瞬变电磁法在煤田采空区勘查及注浆检测中的应用[J]. 地球物理学进展, 29(1): 362-369, doi:10.6038/pg20140151. |
| [57] | 于景邨, 刘志新, 汤金云,等. 2007. 用瞬变电磁法探查综放工作面顶板水体的研究[J]. 中国矿业大学学报, 36(4): 542-546. |
| [58] | 岳建华, 杨海燕, 胡搏. 2007. 矿井瞬变电磁法三维时域有限差分数值模拟[J]. 地球物理学进展, 22(6): 1904-1909, doi:10.3969/j.issn.1004-2903.2007.06.036. |
| [59] | 张保祥, 刘春华. 2004. 瞬变电磁法在地下水勘查中的应用综述. 地球物理学进展, 19(3): 537-541, doi:10.3969/j.issn.1004-2903.2004.03.008. |
| [60] | 张爽, 何胜, 陈曙东. 2014. 高次互感响应对瞬变电磁系统标定的影响[J]. 地球物理学进展, 29(1): 191-196, doi:10.6038/pg20140126. |
 2015, Vol. 30
2015, Vol. 30

