地球物理学进展  2015, Vol. 30 Issue (1): 77-84   PDF    
引用本文
赵永红, 张丹, 王航. 地震预测方法Ⅲ:固体潮与地震[J]. 地球物理学进展, 2015, 30(1): 77-84, doi: 10.6038/pg20150112  
ZHAO Yong-hong, ZHANG Dan, WANG Hang. Earthquake prediction methods Ⅲ: correlation between tidal and earthquake. Progress in Geophysics, 2015, 30(1): 77-84, doi: 10.6038/pg20150112   
地震预测方法Ⅲ:固体潮与地震
赵永红, 张丹, 王航    
北京大学地球与空间科学学院, 北京 100871
收稿日期: 2014-09-09 修回日期: 2014-10-10 .
基金项目：国家自然科学基金项目(40872133, 40821062, 41274094)资助.
作者简介：赵永红, 博士, 教授, 1982年毕业于北京大学地质系, 主要从事地球动力学、实验岩石力学的教学和研究工作. (E-mail: zhaoyh@pku.edu.cn)
摘要：本文从分析研究固体潮与地震发生的相关性的物理机制出发, 探讨了用观测固体潮的方法来预测地震发生的可能性.首先, 根据地震发生的物理力学过程, 给出了地震产生所需要的应力应变条件.实验室岩石力学实验结果和地震应力的观测以及计算结果给出, 完整地壳岩石的强度界于10~103 MPa之间, 断层介质的强度界于1~102 MPa之间.其次, 将固体潮所引起的全球地壳变形在某个活动断裂带附近产生的形变值与地震触发的应变值进行对比, 讨论了固体潮触发地震的可能性.计算分析表明:固体潮在地表对应的应变在10-8的量级, 对岩石介质所引起的应力最高可以达到1.6×10-2 MPa量级, 这样的载荷水平不足以引发地震.最后, 本文结合固体潮观测资料表明, 地震活动性与固体潮的周期性变化无明显相关性, 固体潮对于临震前的含有活动断裂的岩体在某个方向发生地震可能有触发作用, 但是由于这种触发作用与地震发震的时间、地点和震级关系的不确定性, 从而无法用来作为地震预测的方法.
关键词： 地震     固体潮     相关性     物理机制    
Earthquake prediction methods Ⅲ: correlation between tidal and earthquake
ZHAO Yong-hong, ZHANG Dan, WANG Hang    
School of Earth and Space Sciences, Peking University, Beijing 100871, China
Abstract: This paper discussed the possibility of earthquake prediction by tidal observation method by analysis of the correlation between the physical mechanisms of tidal and earthquake. First, the stress-strain conditions for earthquake to occur were introduced according to mechanical process of earthquake. From the observation and result of rock mechanics experiments as well as seismic stress calculation, the strength of crustal rock is between 10~103 MPa, and the strength of fault medium is between 1~102 MPa. Then, the possibility for tidal to trigger the earthquake was analyzed by comparing the global crustal deformation value along the active fault induced by tidal to the critical deformation value for earthquake to happen. Analysis shows that the order of the surface strain corresponding to tidal is around 10-8, induced elastic stress in rock media is around 1.6×10-2 MPa. This load level is not enough to trigger earthquake. Finally, combined with the tidal observation, we demonstrated that there is no significant correlation between seismic activity and cyclical change of tidal. Tidal may play a role in triggering earthquake in rock which has fault in certain direction before breaking occurs. However, there is no obvious correlation among this effect and time, place, magnitude of seismic earthquake. Therefore, tidal can't be used as an earthquake prediction method.
Key words: earthquake     tidal     correlation     physical mechanism    
0 引 言

固体潮与地震发生的相关性一直以来是地球物理学者所关注的问题之一.由于固体潮的发生时间与一些可以观察到的自然现象及地震前兆在时间上有重合之处，所以不少研究人员利用观测和统计的手段试图寻找固体潮与地震发生的相关性.有的研究表明，固体潮可以引起井水水位的周期性变化，而地震孕育和发生所导致的地块的变形也会使得井孔围岩发生形变，从而引起井水位发生变化.通过捕捉井水水位的变化异常，排除固体潮周期性影响因素，寻找哪些水位异常是由于地震孕育过程引起的(刘澜波和郑香媛，1985；李春洪等，1994).Matsumoto等(2003)在日本中部观测深井水位，提取影响水位变化的五个因素，进行时间序列分析：大气压力、潮汐、降水、观测噪声、剩余水位，通过研究发现五个因素都有扰动，不能确定哪一个是造成水位变化的主要原因.还有一些学者将关注点放在井水水位固体潮的加载相应比值上，通过岩石的应力应变的非线性响应，得出这种加载响应率在地震发生前会有较大的变化(张昭栋等，1997).对于固体潮与地震时间序列的关系，Heaton(1975)对以往的资料进行了研究，这些资料对中到大的地震的潮汐应力进行了时间分析，认为部分地区的浅部(<30 km)的震级较大斜滑和走滑断层的地震可能由潮汐应力触发.但是通过统计研究表明没有相应的触发数据与浅层走滑断层地震或者任何中部深部地震有相关性，潮汐应力的触发作用是基于扩容扩散模式，统计模型表明，潮汐与地震触发没有太大的相关性.在对水的直接观察的手段上，根据地下水中一些特征元素的异常变化来探讨固体潮与地震的关系，也是很多学者的研究方向.例如对氡的实测曲线进行分析，发现其变化规律与固体潮周期有契合之处，从而寻找氡的变化与岩石受力的关系，为氡元素的含量与地震发生提供联系，将固体潮与氡联系起来(史勇和张伟，1993).更多的研究者从统计学和波形分析的角度探究二者之间的关系(张雁滨等，1998；杨又陵等，2004；李强和杨军，2004).其他固体潮与地震的相关性的分析方法，还包括通过调和分析求各因子，将观测值用统计学的方法进行组合(Tanaka et al.，2004)，再分离出所需要的波形(冯德益等，1981；吴雪芳，1991)，研究其变化规律，其中调和分析所用的方法为维涅迪克夫法和别尔采夫法.部分学者对加载响应比信号进行了统计研究，Wang等(2004)针对lattice固体地球模型研究了统计稳健性，结果表明在岩石样品破坏的一般时间之前，总体平均加载响应比显著上升，与大地震前观测到的高加载响应比值的现象一致，而对剪切加卸载响应比的测试信号的统计研究也表明，较大的地震事件更容易发生在加卸载相应更高的时候.近些年对于固体潮在地震的前兆分析中采用了一些数理新方法(Sauck，1975；Linde et al.，1992；Wilcock，2001；Tanaka et al.，2002； Tanaka，2010)，包括Z分析、时频分析、参数化谱分析等.以上这些方法重点关注从现象上揭示固体潮与地震发生的相关度，并没有从物理机制上提出二者之间有效的关系.如果将固体潮方法用于地震预测，弄清楚地震发生的物理过程是十分重要的(赵永红等，2014a，2014b)，从中找出与活动断裂带的破坏过程相关的岩石力学性质的变化，对比于固体潮所引起的岩石力学性质的变化，从物理机制上讨论其相关性.本文基于前人所作的固体潮与地震的相关性的研究，对地震的力学过程进行分析，试图找寻固体潮的应力应变能否引起这样一种能量级别下的物理现象，从而探讨二者相关性的物理机制. 1 地震发生的物理力学过程

岩石在受力情况下发生变形，当所受应力超过岩石本身的强度时，岩石发生破坏.而对于有预制裂纹的岩石，岩石破裂的发生地点往往与预制裂纹有着较好的相关性，岩石破坏的强度也小于完整岩石(赵永红等，1993，1995).因此对于地震的发生，需要分两种情况来研究：一是完整地块发生地震时所需要的能量和形变，二是有断裂带出现的情况下地震发生所需要的条件.前人观察可知(陈荣华等，2009)，固体潮可能诱发的地震多发生在断裂带上以及断裂带附近，因此研究发震断裂成为一个主要方向.

发震断裂从平稳变形到发震经历了几个阶段(韦杰，2009)：一为原始阶段，积累应变能，时间漫长；二为临震阶段，应变能积聚到临界状态，应力超过晶体强度，岩石微裂隙产生；三为发震阶段，此时应变能导致岩体体积迅速膨胀，当超过其强度时，岩体发生断裂，能量释放，应力以地震波的形势传播出去(图 1).

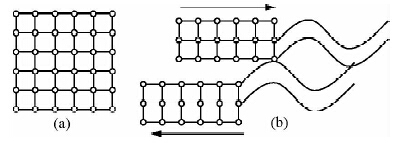图 1(a)原始阶段晶体;(b)断裂阶段晶体，波浪形为地震波.Fig. 1(a)Crystal on original stage;(b)Crystal on broken stage.

根据发生地点的岩体性质和断裂带性质的不同，地震发生所需要的应力应变也不一样.以四川省龙门山断裂带为例，该处发震断裂附近的主要岩性为基底杂岩(姚琪，2012)，这是花岗岩变质后形成的一种岩石.为了探寻其力学性质，以花岗岩为参考标准.花岗岩在常温下的力学性质，以20 ℃的岩石力学实验为例(杜守继，2004)，在应力达到150 MPa，应变达到0.7%~0.8%时，岩石发生破坏，这是完整岩石破裂所需要的力学条件.对于有断裂带存在的条件下，考虑不含流体等干扰因素的简化模型，根据断裂带的特征和实验数据观察，其破坏所达到的应力和应变均小于完整岩体情况，但数量级不会相差太多(杨明芝和马禾青，2011；马胜利等，2003). 2 固体潮力对完整岩体变形破坏过程的影响 2.1 简易模型计算

为了得到固体潮所引起的岩体应力应变的变化情况，建立地球简化模型如图 2.

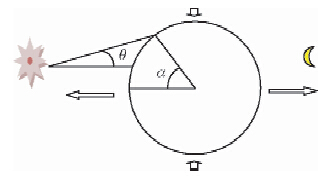图 2 地球所受固体潮力的作用的示意图Fig. 2 Schematic demonstration of tidal force on earth

在南北极方向，地球所受的日月引力导致的形变为压缩，而在赤道方向，忽略黄赤交角因素，地球所受的形变为拉伸.根据万有引力定律，推导出地球上任意一点质量为m的物质受到的日月作用力为

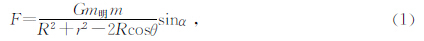
其中θ为地球某点处自转惯性力与地球半径的夹角，α为日月所产生的引力与地球某点处连线与赤道的夹角，R为地球半径，r为日月到地球表面的平均距离，m为质量.代入相关数据进行计算，可以得到，在图中所示点处所受的固体潮力介于赤道拉力最大值约25 Pa和北极压力最大值约13 Pa之间.由于地球模型经过简化，计算会有误差，但可以从数量级上进行判断.2.2 观测值计算

为了更准确的得到固体潮对于岩体形变的影响，前人进行了一些相关的计算研究.在地表正南北、正东西两个方向的线伸缩观测值计算应变的公式为

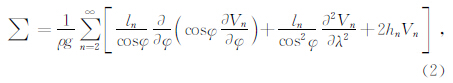
其中ρ为密度，g为重力加速度，Vn为力位，满足拉普拉斯方程，Ln为线度，h为高度(刘序俨等，1988)，由此可计算得到固体潮引起的某局部区域应变观测值最大约为30e-8.根据相关岩石力学参数(表 1).
表 1 相关岩石力学参数 Table 1 Rock mechanics parameters

计算得出讨论区的花岗岩岩体在固体潮作用下产生的应力为

其中应变ε=30e-8，杨氏模量E=5.4e4 MPa.根据前人的相关实验(陈勇和王志亮，2014)，选用岩石样品为黑云母花岗岩，仪器采用武汉岩土所的岩石高压动三轴试验系统.分别加了5种围压，每种围压有4种不同的应变率.比较花岗岩在10-4/s速率下的强度367.9 MPa，在10-3/s时强度为557.86 MPa.Zhao等(1993，1995)Zhao(1998)在实验室岩石力学实验结果和地震应力的观测以及计算结果给出，完整地壳岩石的强度界于10~103 MPa之间，断层介质的强度界于1~102 MPa之间.结合简易模型可以看出，固体潮所产生的应力和应变的量级远不能引起完整的岩体发生破坏. 3 固体潮对含断层岩体的临界状况的影响

自然界中的岩体大多数是不完整的，尤其在地震常发生区域即活动断裂带带附近，岩石破坏强度往往会伴随着断裂带的存在而下降.因此，在考虑完整岩体的破坏条件的基础上，必须考虑有断层因素的情况.如前文计算可以看出，固体潮不能引起完整岩体发生破坏，但是在断裂带的应力积累到一定程度即临界状态时，固体潮所产生的应力或应变有可能是触发地震的诱因之一.在这种情况下，断层与地面的夹角不同，固体潮对断层两盘的作用力也会有变化.下面以三维莫尔圆来说明固体潮所产生的作用力对断层滑动的影响.

根据三维莫尔圆的主应力与剪应力表达式

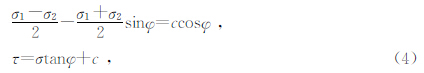
其中σ为正应力，τ为剪应力，φ为剪切角，c为摩擦常数，可得三维莫尔圆的应力状态图.当固体潮所产生的作用力叠加到原始莫尔圆上时，莫尔圆的半径会发生变化，并且莫尔圆会向两边移动.这时可以根据其能否触碰到破裂线来判断在固体潮产生的应力的作用下，岩体能否发生破坏.

根据龙门山地区的地震断层模型数据(石耀霖，2010)，得到最大主应力约为7.5 MPa，最小主应力约为3 MPa，中间主应力为4.2 MPa，发震断层最大主应力和最小主应力的方向北西向60°，地面与断层夹角30°左右，最大潮汐力取数据如表 2(吴小平等，2001).

表 2 固体潮应力值 Table 2 Stress value from tidal

以此绘出在固体潮力的作用下，该含断层岩体的三维莫尔圆的应力状态图(图 3).由图可得，在此地区的固体潮作用下，应力莫尔圆向右移动，半径增大，但是其数量级增加无法与破裂线相切，故在含该断层状态下，固体潮引起岩体破坏的可能性很小，但是也不排除在应力集中非常接近临界状态时，很小的固体潮力也能引起岩体发生破坏.

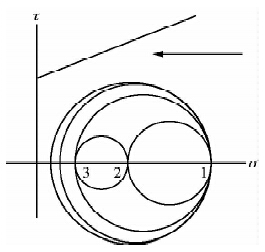图 3 固体潮力作用下的三维应力莫尔圆Fig. 3 Three-dimensional Mohr circle under tidal force
4 固体潮与地震相关性的现象学分析

固体潮与地震的关系的研究主要集中在对地下水的反映、潮汐参数的变化以及波形相位的研究上等.对于地下水的研究主要有水井水位变化的研究和地下水特征元素含量变化的研究，深井水位变化可以有效的记录固体潮和地震波(蔡祖煌，1980；Bower and Heaton，1978；Roeloffs，1998)，承压含水层受到外加构造应力的作用时，地下水的波动微分方程为

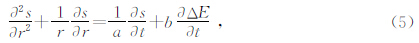
其中s为位移，r为半径，t为时间，E为能量，方程表示了在固体潮作用下地下水位产生的波动，可以对固体潮进行响应.这种解释在含水层中的流体扩散和考虑弹性性能的情况下是可用的，并受到固体潮现象的扰动.通过研究指出井水位对固体潮的响应比较敏感，同时地震也能引起水位的变化，但是二者之间的联系却不是很清楚.对于地震引起的水位变化，汪成明等(1982)对江苏山东等地的20余口井进行了初步调查，发现其可以观察到地下水位振荡现象，但是这种水位变化是地震发生时及发生后所记录到的，它是由地震引起的瑞利波而导致，对于地震前兆的研究意义不大.对于地下水中所含特征元素的观察，史勇和张炜(1993)以氡元素为指标，采用谱分析和滤波，对其时变曲线进行分析.分析方法为将氡的时变曲线进行傅里叶展开，然后利用快速傅里叶变换程序可得氡的时变曲线的振幅谱和相位谱.从谱分析结果可以看到(图 4)，氡的变化潮汐特征明显，在地壳岩石应力没有异常的情况下，氡的时变曲线的变化反映出来的基本上是与固体潮周期一致.当地壳应力发生变化时，氡的时变曲线会有异常发生，这表明氡可以反映地壳应力的变化.
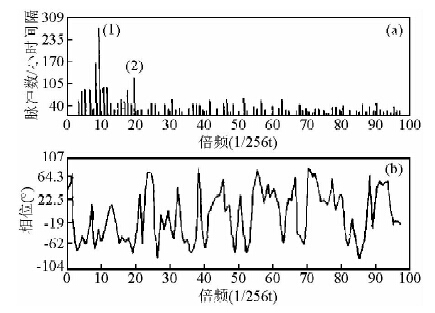图 4 氡时变曲线的振幅谱与相位谱Fig. 4 time spectrum of amplitude and phase in Radon

对于潮汐参数，勒夫数是其中的一种，它具有介质探寻参数特征.勒夫数的变化可以反映地壳的变形，它可以用在固体潮观测资料的计算中(张雁滨等，1998).根据球坐标中的位移分量定义勒夫数H与L为

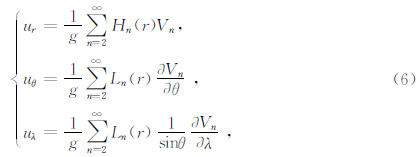
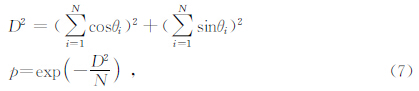
其中，u为形变的三个位移分量，Vn为起潮力位，再经过对固体潮观测资料的处理反演得到二阶勒夫数(刘序俨，1994)，可以反映全球的变形情况和起潮力位.因为一般所需要观测的地震现象位于某个断层带附近，在宏观上是比较局部的一个区域，可以选择勒夫数中的h2来计算讨论(张雁滨等，1998).对于固体潮波形相位，Mohler(1980)把加州1976年6月20日到7月1日之间超过4700次的余震的发生事件与固体潮的相位相比较，其相关性表现在余震爆发时，固体潮可能有利于某些区域的断层运动，而不是在整个序列中连续触发一系列的小的地震事件本身.而根据潮汐相位角的分布情况，Tanaka等(2006)对于过去20年里发生在日本海中部的每个地震事件，借助于计算断层面上的潮汐剪切应力在原始时刻设置了相位角，用统计学的方法测试了相位角是否在一定特定的角度上比较集中对比于能量比较小的地震，计算公式为

其中，θ为潮汐相位角，D为N个事件基础上获得的元素和，P值为显著性水平，计算结果发现没有明显相关性.Métivier等(2009)指出海洋潮汐虽然对地壳有额外的加载，但是并不能够通过足够完整的地震数据库检测到这样的相关性.

对于其它的一些现象，前人也进行了针对性分析.有些学者对能量较小的微震也进行了研究.Glasby和Kasahara(2001)发现潮汐对微震的周期性影响往往是复杂的，因为潮汐在地球表面分布不均匀，而微震又发生在各种各样的地质环境中.很多关于周期性潮汐影响地震的资料都是相对短期的监测，缺乏统计有效性.Ambeh和Fairhead(1991)则发现微震事件以近乎恒定的幅度和规律性发生在有限的范围内，根据该地区的微震发生区域很小，并且该地区接近赤道，潮汐变形最大，作者在验证前猜测此为潮汐触发作用引起.但是考察了半日潮的统计事件后发现，没有相关性(图 5)，左为地震事件，右为潮汐事件.

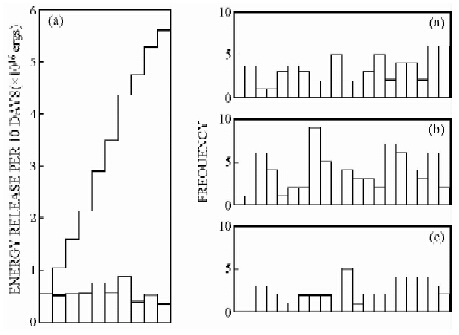图 5 坎麦隆火山微震事件与固体潮的相关性对比图Fig. 5 Correlation between volcano microseismic events and tidal in Cameroon

Rydelek等(1988)也研究了属于微震的火山型地震与潮汐的关系，他们用离散傅里叶数据的方法求出潮汐扰动函数，并没有发现明显的相关性.Knopoff(1970)从月球与地球的关系上来研究相关性，经过统计发现地震与月球近地点时和新月现象的出现时有一定的相关性，但是在大多数地区，却是随机的，根据统计图(图 6)可以看出这种随机性.

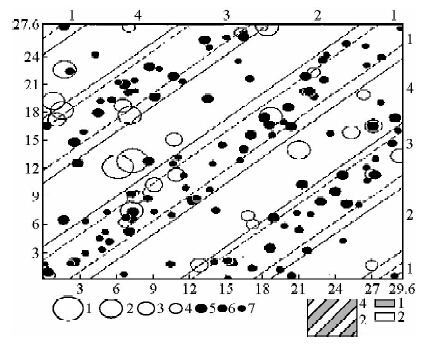图 6 地震事件与月球近地点与新月时刻的关系Fig. 6 Relationship between seismic events and lunar perigee or crescent

Crockett等(2006)指出部分相关性与海潮负荷引发地震的诱因可能一致，在其研究地区的最西段，地震事件与新满月相关性比平均水平高38%.Palumbo(1986)则在此基础上考虑了太阳的因素，他运用了一种通过观察月球和太阳的组合引力的每日变化的方法来测定地震发生的相关性，采用的数据来自于发生在意大利的能量最大的地震事件组合(1900-1983年)，提供了第一个与固体潮的相关性的大型数据库，采用了常规球函数分解的方法为

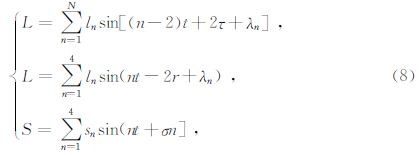
L为月球日变量，S为太阳日变量，n为事件数，t和τ为时间，σ和τ为相位角，研究发现这些大的震动分析没有显著的证据证明意大利的地震由潮汐触发，分析所用的方法为常规球谐函数分解. 5 固体潮与地震活动相关性的观测数据统计

为了验证固体潮与地震发生前兆的相关性，本文对实际发震的情况与固体潮的应力应变的变化情况进行了对比.固体潮的应力和应变数值随时间和经纬度变化的理论值可由公式计算得出，可由图 7反映出变化规律(周江存等，2013)，在一天之内，应力应变的最大值出现两次.研究地震是否由固体潮引起的，需要看在同一区域内，地震发生的时间是否与固体潮的最大应力应变值有相关性.为此统计龙门山地区及周边三年以来的地震信息如表 3(数据来源为中国地震台网http://www.ceic.ac.cn/history)，用统计的方法研究其发震时间的关系如图 8，可以看出，地震在一天内的发震时间分布较为随机，与图 7的固体潮在一天内所产生的两次最大应力和应变无明显相关性.

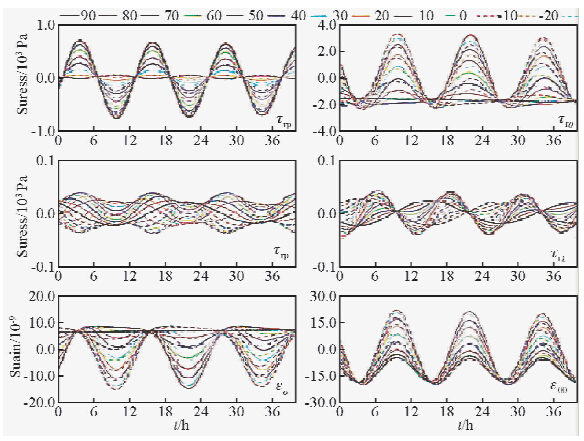图 7 不同纬度处的潮汐应力和应变随时间的变化Fig. 7 Tidal stress and strain changes at different latitudes

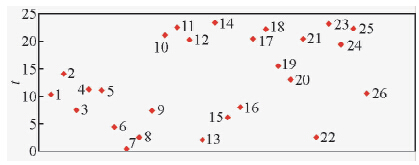图 8 龙门山及周边地区4级以上地震发生日时刻(2012年1月-2014年5月)Fig. 8 Earthquake occurring time(MS>4.0)at Longmen Mountain and the surrounding areas(January，2012~May，2014)

表 3 龙门山及其周边地区的地震发震信息 Table 3 Earthquake information at Longmen Mountain and the surrounding area
6 结论与讨论

本文通过对固体潮与地震发生相关性的物理机制的分析和对大量已有的观测研究结果的总结分析，从地震发生三要素的角度对固体潮引发地震从而用于地震预测的可能性进行了探讨.通过分析和研究可得出如下结论：

(1)固体潮所产生的作用力最高为1.6×10-2 MPa，其数量级远远小于完整岩石10~103 MPa或者含断层岩石1~102 MPa的强度，因此固体潮不能够直接引起地震的发生.

(2)在临界状态下，固体潮的作用对含断层岩体所引起的应力可能在某个方向上触发断层滑动，但是相关性很小.尽管在某些地区，正断层和走滑断层比逆断层显得好像容易被固体潮触发，没有明显的统计学证据证明它是基于震源机制的地震触发.

(3)固体潮的每日变化与地震发生的时间没有明显的相关性，固体潮作用力所产生的一日内的最大应力应变值并不是引起地震发生时间的原因.

对于发震前的不同的临界状态下的孕震岩体，其所存储的应变能具体数值是多少，还需要多少的应力和应变就能发生破坏，固体潮对于什么样的孕震条件下的岩体可以起到触发地震的作用，这些都需要多角度的研究思路和进一步的深入研究才能做回答.

对于地震发生的地点，前人的计算模型与实际地震数据对比得出，固体潮在地球上所产生的应力最大值的地点，并不一定是地震的多发地点，地震的发生更多的取决于断裂带的位置与走向.对于地震发生的时间，固体潮是周期性行为，而地震的发生时间是随机性的，不存在明显的周期性.对于震级，地震的震级主要是由孕震岩体所积累的弹性能能量大小决定. 因此，固体潮对于临震前的含有活动断裂的岩体在某个方向发生地震可能有触发作用，但是由于这种触发作用与地震发震的时间、地点和震级关系的不确定性，无法用固体潮作为地震预测的方法之一.

参考文献
[1] Ambeh W B, Fairhead J D. 1991. Regular, deep seismicity beneath Mt Cameroon volcano: lack of evidence for tidal triggering[J]. Geophys. J. Int., 106(1): 287-291.
[2] Bower D R, Heaton K C. 1978. Response of an aquifer near Ottawa to tidal forcing and the Alaskan earthquake of 1964[J]. Canadian Journal of Earth Sciences, 15(3): 331-340.
[3] Bredehoeft J D. 1967. Response of well-aquifer systems to earth tides[J]. J. Geophys. Res., 72(12): 3075-3087.
[4] Cai Z H. 1980. Earth tides and seismic waves recorded by the level fluctuations in a deep borehole at Wali near Beijing[J]. Acta Seismologica Sinica (in Chinese), 2(2): 205-214.
[5] Chen Y, Wang Z L. 2014. A study of the dynamic behavior and failure criterion of the granite in Huashan (in Chinese)[J]. Hydrogeology & Engineering Geology (in Chinese), 41(3): 66-69.
[6] Chen R H, Zhang J, Li Z H. 2009. Two examples of the solid tide stress triggering significant shocks before a large earthquake[J]. Inland Earthquake (in Chinese), 23(4): 413-416.
[7] Crockett R G M, Gillmore G K, Phillips P S, et al. 2006. Tidal synchronicity of the 26 december 2004 sumatran earthquake and its aftershocks[J]. Geophysical Research Letters, 33(19), doi: 10.1029/2006GL027074.
[8] Du S J, Liu H, Zhi H T, et al. 2004. Testing study on mechanical properties of post-high-temperature granite[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 23(14): 2359-2364.
[9] Feng D Y, Gu J P, Luo R M, et al. 1981. Tne statistical indexes of seismicity and the probability prediction for the time of earthquake occurrence[J]. Journal of Seismological Research (in Chinese), 4(1): 1-9.
[10] Glasby G P, Kasahara J. 2001. Influence of tidal effects on the periodicity of earthquake activity in diverse geological settings with particular emphasis on submarine hydrothermal systems[J]. Earth-Science Reviews, 52(4): 261-297.
[11] Hartzell S, Heaton T. 1989. The fortnightly tide and the tidal triggering of earthquakes[J]. Bulletin of the Seismological Society of America, 79(4): 1282-1286.
[12] Heaton T H. 1975. Tidal triggering of earthquakes[J]. Geophys. J. Int., 43(2): 307-326.
[13] Heki K. 2003. Snow load and seasonal variation of earthquake occurrence in Japan[J]. Earth and Planetary Science Letters, 207(1-4): 159-164.
[14] Hu H, Wang R, Li X M. 2000. Force caused by luni-solar tide and earthquake[J]. Publications of the Yunnan Observatoty (in Chinese), (4): 101-104.
[15] Knopoff L. 1970. Correlation of earthquakes with lunar orbital motions[J]. The Moon, 2(2): 140-143.
[16] Li Q, Yang J. 2004. Research on variation of tilt tidal factor before south yellow sea Ms6. 1 earthquake[J]. Journal of Geodesy and Geodynamics (in Chinese), 24(3): 84-86.
[17] Li C H, Chen Y H, Tian Z J, et al. 1990. Theory of the response of well—aquifer system to earth tides and its application[J]. Hydrogeology and Engineering Geology (in Chinese), (6): 10-13.
[18] Linde A T, Gladwin M T, Johnston M J S. 1992. The loma prieta earthquake, 1989 and earth strain tidal amplitudes: an unsuccessful search for associated changes[J]. Geophysical Research Letters, 19(3): 317-320.
[19] Liu L B, Zheng X Y. 1985. The analysis results of water-well earth tides and their applications to earthquake prediction[J]. Earthquake (in Chinese), (1): 7-12.
[20] Liu X Y, Li P, Zhang Y B. 1988. Calculation of theoretical value of cubic expansion tide and its harmonic analysis[J]. Crustal Deformation and Earthquake (in Chinese), 8(4): 354-358.
[21] Liu X Y. 1994. Analysis on earth strain tide of guza seismic station[J]. Acta Geophysica Sinica (in Chinese), 37(Suppl.2): 213-221.
[22] Métivier L, de Viron O, Conrad C P, et al. 2009. Evidence of earthquake triggering by the solid earth tides[J]. Earth and Planetary Science Letters, 278(3-4): 370-375.
[23] Ma S L, Liu L Q, Ma J, et al. 2003. A discussion on related issues of physical process of faulting and strong earthquake based on experimental results[J]. Earth Science Frontiers (in Chinese), 10(1): 225-232.
[24] Matsumoto N, Kitagawa G, Roeloffs E A. 2003. Hydrological response to earthquakes in the Haibara well, central Japan–I. Groundwater level changes revealed using state space decomposition of atmospheric pressure, rainfall and tidal responses[J]. Geophys. J. Int., 155(3): 885-898.
[25] Mohler A S. 1980. Earthquake/earth tide correlation and other features of the Susanville, California, earthquake sequence of June-July, 1976[J]. Bulletin of the Seismological Society of America, 70(5): 1583-1593.
[26] Palumbo A. 1986. Lunar and solar tidal components in the occurrence of earthquakes in Italy[J]. Geophys. J. R. Astr. Soc., 84(1): 93-99.
[27] Roeloffs E A. 1998. Persistent water level changes in a well near Park field, California, due to local and distant earthquakes[J]. JGR, 103(B1): 869-889.
[28] Rydelek P A, Davis P M, Koyanagi R Y. 1988. Tidal triggering of earthquake swarms at Kilauea Volcano, Hawaii[J]. JGR, 93(B5): 4401-4411.
[29] Sauck W A. 1975. The brawley, California earthquake sequence of January, 1975, and triggering by earth tides[J]. Geophysical Research Letters, 2(11): 506-509.
[30] Shi Y, Zhang W. 1993. The mechanical basis of earthquake prediction in radon[J]. Acta Seismologica Sinica (in Chinese), 15(1): 103-108.
[31] Tanaka S, Ohtake M, Sato H. 2002. Spatio-temporal variation of the tidal triggering effect on earthquake occurrence associated with the 1982 South Tonga earthquake of Mw 7. 5[J]. Geophysical Research Letters, 29(16): 3-1-3-4.
[32] Tanaka S, Ohtake M, Sato H. 2004. Tidal triggering of earthquakes in Japan related to the regional tectonic stress[J]. Earth, Planets and Space, 56(5): 511-515.
[33] Tanaka S, Sato H, Matsumura S, et al. 2006. Tidal triggering of earthquakes in the subducting Philippine Sea plate beneath the locked zone of the plate interface in the Tokai region, Japan[J]. Tectonophysics, 417(1-2): 69-80.
[34] Tanaka S. 2010. Tidal triggering of earthquakes precursory to the recent Sumatra megathrust earthquakes of 26 December 2004 (Mw 9. 0), 28 March 2005 (Mw 8. 6), and 12 September 2007 (Mw 8. 5)[J]. Geophysical Research Letters, 37(2), doi: 10.1029/2009GL041581.
[35] Wang C M, Zhuo M B, Guo Y X, et al. 1983. Oscillation in deep well level caused by earthquake[J]. Earthquake (in Chinese), (2): 34-38.
[36] Wang Y C, Mora P, Yin C, et al. 2004. Statistical tests of load-unload response ratio signals by lattice solid model: implication to tidal triggering and earthquake prediction[J]. Pure Appl. Geophys., 161(9-10): 1829-1839.
[37] Wei J. 2009. Discussion on the mechanism of the Wenchuan earthquake and Geodynamics (in Chinese)[C].//Analysis Investigation and Research about Earthquake Damage in Projection. Beijing: Rock Mechanics and Engineering Society of China, 88-93.
[38] Wilcock W S D. 2001. Tidal triggering of microearthquakes on the Juan de Fuca Ridge[J]. Geophysical Research Letters, 28(20): 3999-4002.
[39] Wu X F. 1991. Theoretical basis and method for earthquake prediction by earth tide[J]. Earthquake (in Chinese), (1): 8-14.
[40] Wu X P, Huang Y, Hu J F, et al. 2001. Calculation of additional tidal stress along seimic principle stress orientation and study on its action mode on seismogenic fault[J]. Journal of Seismological Research (in Chinese), 24(1): 48-54.
[41] Yang M Z, Ma H Q. 2011. Variation of energy field of Longmenshan fault zone before the Wenchuan Ms8. 0 earthquake[J]. Earthquake Research in China (in Chinese), 27(3): 260-267.
[42] Yang Y L, Liu H, Jiang C K, et al. 2004. Preliminary study of the relations between the observation of deformation earth tide and the mid-strong earthquakes in Xinjiang[J]. South China Journal of Seismology (in Chinese), 24(1): 1-9.
[43] Yao Q, Xing H L, Xu Q W, et al. 2012. Influence of lithologic differences on either walls of the fault on the Wenchuan earthquake[J]. Chinese Journal of Geophysics (in Chinese), 55(11): 3634-3647, doi: 10.6038/j.issn.0001-5733.2012.11.012.
[44] Zhang Y B, Jiang J, Li X D, et al. 1998. Tidal integrated elastic characteristic parameters and its precursory anomaly evolution[J] Acta Seismologica Sinica (in Chinese), 20(4): 388-393.
[45] Zhang Z D, Chen X Z, Chen J M, et al. 1997. Precursor of earthquake in unload response ratio from water well changed by tidal[J]. Acta Seismologica Sinica (in Chinese), 19(2): 174-180.
[46] Zhang Z D, Zheng J H, Geng J, et al. 2002. Physical mechanism and unitary mathematical equation for tidal phenomena of ground water[J]. Seismology and Geology (in Chinese), 24(2): 208-214.
[47] Zhao Y H, Huang J F, Wang R. 1993. Real-time SEM observations of the microfracturing process in rock during a compression test[J]. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr.(in Chinese), 36(4): 453-462.
[48] Zhao Y H, Huang H, Hou J J, et al. 1995. Experimental study of meso-fractures in rock and its implication for understanding seismic activities[J]. Chinese Journal of Geophysics (in Chinese), 38(5): 627-636.
[49] Zhao Y H. 1998. Crack pattern evolution and a fractal damage constitutive model for rock[J] Int. J. Rock Mech. Min. Sci., 35(3): 349-366.
[50] Zhao Y H, Wang H, Yang J Y, et al. 2014a. Earthquake prediction methods Ⅱ: comment[J]. Progress in Geophysics (in Chinese), 29(2): 630-637, doi: 10.6038/pg20140221.
[51] Zhao Y H, Yang J Y, Hui H J, et al. 2014b. Earthquake prediction methods Ⅰ: review[J]. Progress in Geophysics (in Chinese), 29(1): 129-140, doi: 10.6038/pg20140117.
[52] Zhou J C, Sun H P, Xu J Q, et al. 2013. Tidal strain and tidal stress in the earth's interior[J]. Chinese Journal of Geophysics (in Chinese), 56(11): 3779-3787, doi: 10.6038/cjg20131119.
[53] 蔡祖煌. 1980. 北京洼里深井水位变化所记录的地球固体潮和地震波[J]. 地震学报, 2(2): 205-214.
[54] 陈勇, 王志亮. 2014. 华山花岗岩动力学行为与破坏准则研究[J]. 水文地质工程地质, 41(3): 66-69.
[55] 陈荣华, 张晶, 李志海. 2009. 固体潮应力对大地震前显著地震触发的两个例子[J]. 内陆地震, 23(4): 413-416.
[56] 杜守继, 刘华, 职洪涛,等. 2004. 高温后花岗岩力学性能的试验研究[J]. 岩石力学与工程学报, 23(14): 2359-2364.
[57] 冯德益, 顾瑾平, 罗瑞铭,等. 1981. 地震活动的统计指标与发震时间的概率预报[J]. 地震研究, 4(1): 1-9.
[58] 胡辉, 王锐, 李晓明. 2000. 日月引潮力与地震[J]. 云南天文台台刊, (4): 101-104.
[59] 李强, 杨军. 2004. 南黄海6.1 级地震前倾斜潮汐因子变化研究[J]. 大地测量与地球动力学, 24(3): 84-86.
[60] 李春洪, 陈益惠, 田竹君,等. 1990. 井-含水层系统对固体潮响应的理论及其应用[J]. 水文地质工程地质, (6): 10-13.
[61] 刘澜波, 郑香媛. 1985. 井水固体潮分析结果及其在地震预报中的应用[J]. 地震, (1): 7-12.
[62] 刘序俨, 李平, 张雁滨. 1988. 地表的面应变和体应变固体潮理论值计算及其调和分析[J]. 地壳形变与地震, 8(4): 354-358.
[63] 刘序俨. 1994. 应变固体潮主应变及剪应变的计算──四川姑咱台应变固体潮分析[J]. 地球物理学报, 37(增刊2): 213-221.
[64] 马胜利, 刘力强, 马瑾,等. 2003. 基于实验结果讨论断层破裂与强震物理过程的若干问题[J]. 地学前缘, 10(特刊1): 225-232.
[65] 史勇, 张炜. 1993. 以氡报震的力学基础——氡与固体潮的关系[J]. 地震学报, 15(1): 103-108.
[66] 汪成民, 卓明葆, 郭一新,等. 1983, 地震引起的深井水位振荡现象[J]. 地震, (2): 34-38.
[67] 韦杰. 2009. 浅论汶川地震机制与地球动力学机理[C]. //汶川大地震工程震害调查分析与研究. 北京: 中国岩石力学与工程学会, 88-93.
[68] 吴雪芳. 1991. 固体潮预报地震的理论基础与方法[J]. 地震, (1): 8-14.
[69] 吴小平, 黄雍, 胡家富,等. 2001. 地震主应力方向的附加潮汐应力计算及其对发震断层的作用方式研究[J]. 地震研究, 24(1): 48-54.
[70] 杨明芝, 马禾青. 2011. 汶川8. 0 级地震前龙门山断裂带能量场变化[J]. 中国地震, 27(3): 260-267.
[71] 杨又陵, 刘辉, 江崇昆,等. 2004.新疆形变固体潮观测与中强地震关系的初步研究[J] 华南地震, 24(1): 1-9.
[72] 姚琪, 邢会林, 徐锡伟,等. 2012. 断裂两盘岩性差异对汶川地震的影响[J]. 地球物理学报, 55(11): 3634-3647, doi: 10.6038/j.issn.0001-5733.2012.11.012.
[73] 张雁滨, 蒋骏, 李旭东,等. 1998. 固体潮综合弹性特征参数及其前兆异常演化[J]. 地震学报, 20(4): 388-393.
[74] 张昭栋, 陈学忠, 陈建民,等. 1997. 井水位固体潮加卸载响应比的地震短临前兆[J]. 地震学报, 19(2): 174-180.
[75] 张昭栋, 郑金涵, 耿杰,等. 2002. 地下水潮汐现象的物理机制和统一数学方程[J]. 地震地质, 24(2): 208-214.
[76] 赵永红, 黄杰藩, 王仁. 1993. 破裂带发育的SEM实验研究及其对地震前兆的启示[J]. 地球物理学报, 36(4): 453-462.
[77] 赵永红, 黄杰藩, 候建军,等. 1995. 岩石细观破裂的实验观测研究及其对认识地震活动性的启示[J]. 地球物理学报, 38(5): 627-636.
[78] 赵永红 王航 杨家英,等. 2014a. 地震预测方法II: 评述[J]. 地球物理学进展, 29(2): 630-637, doi: 10.6038/pg20140221.
[79] 赵永红 杨家英 惠红军,等. 2014b. 地震预测方法I: 综述[J]. 地球物理学进展, 29(1): 129-140, doi: 10.6038/pg20140117.
[80] 周江存, 孙和平, 徐建桥,等. 2013. 地球内部应变与应力固体潮[J]. 地球物理学报, 56(11): 3779-3787, doi: 10.6038/cjg20131119.