2. 成都理工大学地球物理学院, 成都 610059;
3. 中国地质科学院地质力学所, 北京 100081;
4. 中国地质科学院, 北京 100037
2. Institute of Geophysics, Chengdu University of technology, Chengdu 610059, China;
3. Institute of Geomechanics, Chinese Academy of Geological Sciences, Beijing 100081, China;
4. Chinese Academy of Geological Sciences, Beijing 100037, China
近几十年,利用地震仪记录到的天然地震信号探索地球内部地震波速度结构取得了丰硕的成果.但是由于大多数地震只是发生在活动的地质构造板块边界,所以大部分的地区是无法获取地震信息的.近些年兴起的背景噪声层析成像技术极大的改善了因为震源分布不均匀反演速度结构时所导致的问题,为研究地球的内部结构提供了有力的工具.50多年以前,Aki(1957)从理论地震学方法预计背景噪声可以用来获得面波在台阵下方的传播速度(Prieto,2012);随着观测仪器的改进以及计算性能的提高,曾经理论的设想如今在实际应用中已经获得应用.
Weaver和Lobkis(2001)Lobkis和Weaver(2001)的声学实验展示出两个接受器叠加的互相关函数等同于他们之间的格林函数;这个具有开创意义的工作被Shapiro和Campillo(2004)和Shapiro 等(2005)应用到地震学界.将一对台站的背景噪声地震波形记录进行互相关并叠加之后,相干信号就会从白噪声一般的记录中浮现出来.所提取的信号就是格林函数,对其进行分析就可以获得面波在两个台站之间的传播速度和频散曲线(Prieto,2012;Li et al., 2010).在之后的研究中,从叠加的互相关函数中获取面波的相速度和群速度已经成为背景噪声层析成像的标准流程(Lin et al., 2008;Gorbatov et al., 2013).
天然地震总是有特定的地理分布,这在一定程度上限制了地震数据分析的方法;同时,由于难以准确获得震源位置以及破裂过程的信息,更使得利用天然地震信号全面分析地球内部结构较困难(Prieto,2012).而利用背景噪声技术叠加得到的互相关函数等同于点源脉冲从一个台站传播到另一个台站的地震图(Stehly,2009),相当于地震的震源位置和破裂过程都是已知的,同时台站的位置可以根据研究对象的需要而布设.相对于天然地震数据而言,背景噪声技术获得的面波优势在于(Li et al., 2010a):
(1)任意两个台站之间都可以得到格林函数,这大大提高了射线覆盖率,而且方位角覆盖更均匀;.
(2)背景噪声并不依靠地震事件.
(3)可以获得更短周期的面波信息,天然地震数据得到的频散曲线周期范围在15~20 s以上,背景噪声则可以低至4~6 s.从背景噪声里获得的短周期(小于20 s)面波有效地提高了地壳内部成像的精度(Lin et al., 2008;Bensen et al., 2008; Poli et al., 2012).
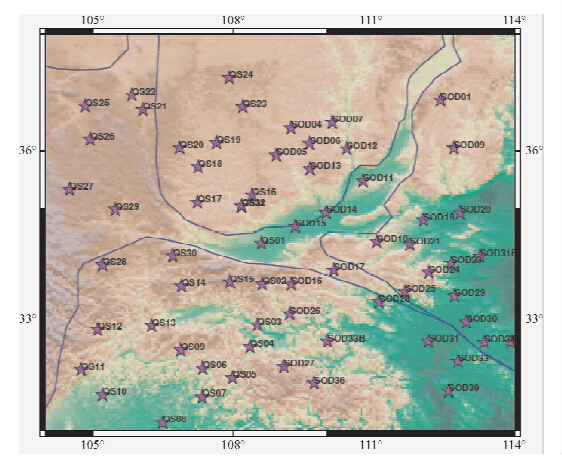 | 图 1 本文的研究区域—秦岭地区.QS和SOD台站分别是地科院和北京大学架设Fig. 1 Study area and station locations. QS- and SOD-stations were installed by CAGS and Peking University respectively |
Campillo &和Paul(2003)和Paul 等(2005)展示出Love波可以像Rayleigh波一样被提取出来.而早期的探索工作首先集中在地震记录的垂直分量上,也就是Rayleigh面波,在取得了卓有成效的结果之后,学术界逐渐探索对地震记录的水平分量也开始运用背景噪声方法来提取Love波(Lin et al., 2008;Li et al., 2010b).对于Love波的研究晚于Rayleigh波,这是由于水平分量上的信噪比较低,所以互相关函数在叠加的时候,相干信号—也就是Love波并不是像Rayleigh波明显,Love波频散曲线的频带宽度相应的也比Rayleigh波要窄一些.
在能量均分的假设下,各个弹性模式的振幅是一样的,Weaver和Lobkis(2001)在理论上证明了互相关叠加可以得到两台站间的格林函数.而在实际的地震数据处理中,有两个条件影响了叠加的互相关函数与格林函数之间的数学关系.首先就是各个模式的能量并不是均分的,在互相关函数叠加的时候权重就不是一样的了;第二就是噪声源并不是均匀分布的,这使得在地球表面的积分用离散的求和代替时会产生不可避免的偏差.在能量不是均分在各个模式,噪声源不是均匀分布在地球表面的时候,相干的信号在叠加的时候就难以得到加强,得到的互相关函数信噪比就会较低.Schimmel和Paulssen(1997)提出了phase-weighted-stack(PWS)方法,在多道信号叠加的过程中,有效的压制了不相干信号—也就是真正的噪声,并提高了相干信号的强度.在叠加互相关函数获取Love波的过程中,本文采用了PWS这种技术;其结果与传统的线性叠加结果相比起来确实提高了格林函数的信噪比,拓宽了频散曲线的周期范围.
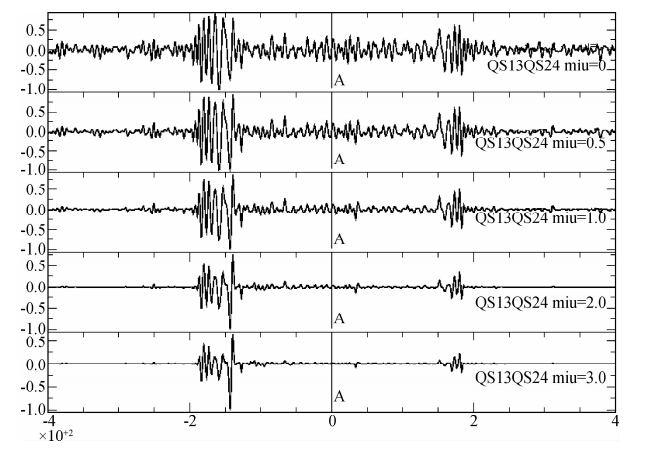 | 图 2 QS13-QS24之间的Love波互相关函数.从上到下,指数为0,0.5,1,2,3Fig. 2 Cross correlation functions between QS13 and QS24 stations. Index is 0,0.5,1,2,3 from to bottom |
在叠加得到任意两个台站之间的Love波互相关函数之后,本文应用Frequency Time domain Analysis(FTAN)分析得到各个台站对之间的相速度和群速度,在这个过程中还用到了Phase Matched Filter(Levshin et al., 1992).进而通过层析成像得到了研究区域的相速度分布,进一步做了三维 SH波速度反演.在分层介质中,Love波是由于SH波耦合产生的.Love波的相速度和群速度与介质的密度和SH波速度有关,对SH波的敏感度远大于对密度的敏感度,即使是在横向各向同性的情况下,Love波对于SV的敏感度也是可以忽略的(Widmer-Schnidrig and Laske, 2007).面波反演对于初始模型依赖较强,选择一个贴合实际的模型对于面波反演十分重要,本文选择的初始模型为稍加修改的crust 2.0(Bassin et al., 2000).正演程序为在平行层状介质中求解Love波频散曲线,在阻尼最小二乘意义下通过拟合频散曲线来寻找最优化模型的解.为了得到地壳厚度,在SH波反演过程中,Moho面的深度也作为变量参与反演.在利用面波反演剪切波速度结构的方法中,有一种是对各个观测台站进行反演,之后把结果拼合起来得到一个三维的结构.本文的反演并不是逐个台站的一维反演,而是三维反演.反演未知量是研究区域里所有单元里的SH波速度和Moho深度,通过建立一个大型的矩阵方程,包含水平向Laplace平滑,在阻尼最小二乘意义下求解得到三维 SH波速度结构.
本文将这种技术应用到了北京大学与中国地质科学院合作布设在秦岭造山带及其周边地区的(69台)流动地震台阵,利用台站的水平分量噪声记录提取的Love波频散曲线来获得台站间Love波相、群速度,进而得到了从6 s到30 s周期的Love波相速度二维分布图像.进一步进行了三维SH波速度反演.近东-西走向的秦岭造山带横亘中国中部,是分割中国南方(扬子块体)、北方(华北块体)的重要造山带,对于中国大陆构造的形成与演化起着重要的控制作用(袁学诚等,1994;何建坤等,1998).它的形成和演化经历了古生代秦岭大洋岩石圈向华北板块下的俯冲消减、中三叠世华北板块与扬子板块的对接和碰撞等复杂的地质演化过程(滕吉文等,2006).研究区地壳和上地幔SH波三维速度结构的获得,为进一步研究秦岭造山带构造运动和上地幔动力学提供基础观测资料.
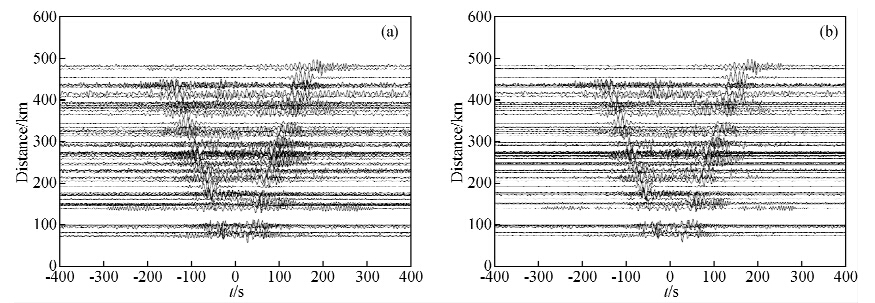 | 图 3(a)QS01与其他台站之间的线性叠加得到的互相关函数;(b)QS01与其他台站之间的PWS算法得到的互相关函数,指数选取为0.5.噪声水平比(a)要低.Fig. 3(a)CCFs with respect to QS01 station using linear stack method; (b)CCFs with respect to QS01 station using PWS with power 0.5. Noise level here is lower than in(a). |
应用地震学方法来研究地壳和上地幔开始于上世纪初期,从此以后地震为地学家认识地球提供了强有力的数据来源,但是稀少的天然地震并不能得到高精度的地球模型.在过去的几年内,蓬勃发展的背景噪声方法为科学家了解地壳和上地幔的精细结构提供了可靠的信息来源.对于背景噪声成像的研究一直在进行,Bense等(2007)非常详细的介绍了处理流程与方法.背景噪声方法能够获得很低周期的频散信息,这使得地震学家能够准确地认识地壳以及上地幔的速度结构(Tang et al., 2013).
Love波的研究并没有Rayleigh波那么广泛(如,Li et al., 2010a,b),但研究Love波的特点在于,这个波并不依赖于P波速度,而只与SH波有关,所以在做反演的时候要求解的参数会少一些,同时矩阵奇异性也会降低.Phase-Weighted-Stack(PWS)方法提高了信噪比,增强了互相关叠加的格林函数.本文先对采用PWS方法得到的互相关函数应用FTAN求取Love波频散曲线,之后应用Barmin等(2005)的原理得到不同周期的二维Love波相速度分布图像,周期范围从6s到30s.对传统线性叠加得到的互相关函数做同样的处理,得到的二维相速度周期范围就窄一些,未曾达到30s.不同周期的Love波二维相速度分布与秦岭地区的地质背景是一致的.
在根据Love波频散曲线反演SH波速度结构的时候,考虑到面波反演十分依赖于初始模型,所以采用了crust 2.0(Bassin et al., 2000)模型作为初始输入模型,之后应用LSQR算法(Lawson et al., 1979;Paige and Saunders, 1982a,b)求解矩阵方程.在应用LSQR求解矩阵方程的时候,阻尼参数的选取是在测试了一系列数值之后,在得到的L形曲线上选取的.值得说明的是,本研究并不是一个点一个点的一维反演,然后拼合成区域剪切波速度模型,而是同时反演整个研究区域的SH波速度模型,得到的是一个三维的结果. 1.1 数据
自2011年初开始,北京大学与中国地质科学院合作,在秦岭造山带及周边地区开展流动地震台阵观测,共安装了69台流动宽频带地震台站.北京大学安装36台仪器,地震仪类型为3ESP,3ESPC和Trillium三种,采集系统记录仪分别为reftek130和Taurus,其中有6台Taurus宽频带地震仪来自武汉大学,来自这36个台站的数据时间跨度为2011年4月到2011年9月,采样率全部为40 Hz.中国地质科学院安装的30台流动台站全部为3ESP地震仪,数据采集系统为reftek 130,时间为2011年8月至2012年9月,采样率为100 Hz.经过筛选,在这69个台站中,本文针对61个台站的数据获得了互相关函数并参与面波层析成像.主要流程见表 1.
|
|
表 1 本研究数据处理流程 Table 1 Processing procedures in this article |
由于记录仪不一样,本研究的第一步是将reftek和Taurus记录到的数据转换为统一的SAC格式,之后将这些连续的波形记录截成每天一个文件.台站的地震摆类型不一致,所以在做互相关之前所有的连续波形记录都要去除仪器响应,并去除平均值和线性倾向; 其中带通滤波器参数也被加入到了去除仪器响应的命令中(这些命令都是在Seismic Analysis Code-SAC下完成的).面波数据处理并不需要高频的记录,所以本研究在互相关之前对所有数据用SAC进行了降采样,降采样之后的数据大大节省了硬盘空间,同时加快了数据处理进程.本研究主要依据Bensen等(2007),Lin等(2008)以及 Schimmel和Paulssen(1997)编制FORTRAN程序来完成互相关函数的计算与叠加. 1.2.1 单台数据处理
在频率域内做互相关只需要两次快速傅里叶变换以及一次向量相乘,速度要比在时间域内快得多.而且由于连续波形记录需要进行谱白化,所以在频率域内做互相关是一种较好的选择.单挑数据处理包括时间域内的归一化和频率域内的谱白化.
时间域内归一化的目的是去除地震信号以及数据记录中不规则的异常值(Bensen et al., 2007; Lin et al,2008).在背景噪声理论中,地震信号会影响格林函数的准确性,而记录中太大的异常会使信号部分对互相关的贡献变弱,所以都要及早去除.在去除仪器响应的命令中,本研究采用的带通滤波范围为5~100 s.天然地震信号的面波在15~50 s的范围内十分明显,所以将经过第2步处理的记录在这个频带内进行滤波,取其绝对值并用移动时窗平滑(在Bensen等(2007)文章中被称为running absolute mean normalization),然后以水平两道中较大者之倒数作为权重同时作用到相应的水平两道各点上.经过时间域内的归一化之后,每一条记录的波谱并不是平坦的;紧接着进行的谱白化就是要扩宽背景噪声信号的频谱宽度.在频率域内,水平两道记录的振幅经过平滑后,选择对应各点较大的值的倒数作为两道数据共同的权重.频率域内的谱白化与时间域内的归一化操作思想是相似的,都是为了使信号在相应的域内变得更平滑.
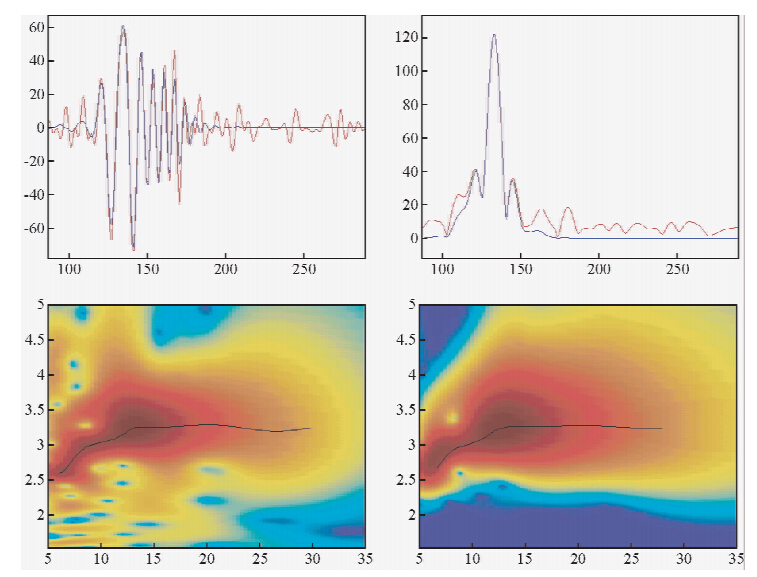 | 图 4 FTAN分析.左上图:蓝色波形为QS24和QS28之间经过242天数据叠加得到的互相关原始波形,红色为清除了噪声之后的波形.左下图:原始FTAN图像和测量的群速度(黑线).右上图:红色为压缩信号,蓝色为截取的压缩信号.右下图:经过Phase Matched Filter之后的FTAN图像和测量的群速度(黑线)Fig. 4 FTAN. Raw(blue) and cleaned(red)waveforms between stations QS24 and QS28 after 242 days stack(Top Left). Raw FTAN diagram and measured group velocity(Bottom Left). Compressed signal(red) and cleaned signal(blue)(Top Right). Cleaned FTAN diagram and measured group velocity with Phase Matched Filter(Bottom Right) |
对每一对水平向记录进行时间域归一化和频率域谱白化之后,在频率域内对任意两个台站对进行各个分量的互相关,并将每一天的互相关结果叠加起来就得到了最后的能够看得出信号的互相关函数.每两个台站都能得到4个互相关分量,分别是E-E,E-N,N-N,N-E.在获取Love波信号的处理中,本研究的处理流程参考的是Lin 等(2008).先做各道的互相关,之后再旋转,这样做的好处是既节省了硬盘存储空间,又加快了处理进程.需要注意的是,在做单台法处理的时候,一定要对水平两道选择同样的权重,只有这样才能保证单台处理步骤与旋转算法是可以互换的.把每天的互相关函数叠加起来而不加权重得到的是传统线性叠加互相关函数.通常情况下,这种线性叠加导致的是低信噪比波形,而且在互相关函数的零时刻点附近出现虚假的波包.这种虚假波包的现象可以从理论公式中寻找一些答案:(1)震源分布不均匀,背景噪声也是有大致固定的噪声源,比如海洋;(2)理论推导过程中的能量均分假设并不符合实际.
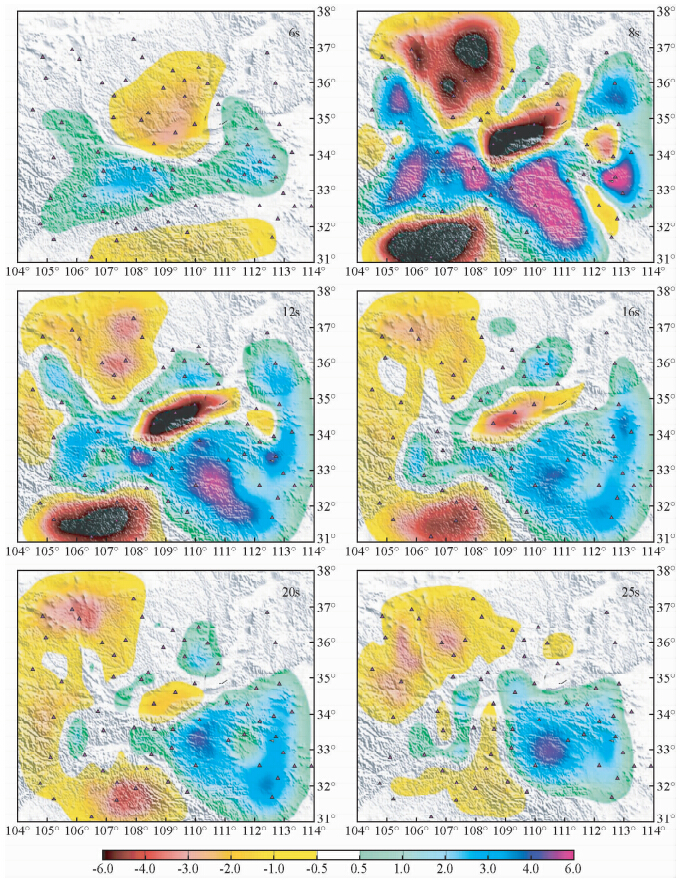 | 图 5 Love波在不同周期的相速度分布图Fig. 5 Tomography of Love wave phase velocities at several periods |
正是因为实际处理过程中存在着并不符合数学理论假设的条件,所以一些研究开始探索如何从叠加的算法进行改进以便提高互相关函数的信噪比(Prieto and Beroza, 2008;Baig et al., 2009;Kimman,2011).Schimmel和Paulssen(1997)提出的PWS是一种非线性的算法,主要应用于压制噪声,提高信号强度.首先,计算所有序列的归一化谱函数,这可以通过先做傅里叶变换,然后除以其振幅,之后在除以叠加序列的个数,这其实就是一个相位叠加函数;其次,将线性叠加得到的互相关函数乘以第一步得到的相位叠加函数的绝对值.在做第二步操作的时候,可以对相位叠加函数取一个指数运算,当指数取为0的时候就是传统的线性叠加运算;跟线性叠加的互相关函数比较而言,指数越大,波形畸变越严重,而信噪比则提高很大,无畸变波形与高信噪比是不可兼得的.在比较了0,0.5,1.0,2.0,3.0这几个指数后,本研究最终采用了0.5,保证了波形在不受到太大影响的情况下提高了信噪比.与传统线性叠加互相关函数相比,PWS得到的互相关函数里的Love波信号并没有收到太大畸变,同时其噪声部分得到了压制,也就是信噪比得到了提高. 1.2.3 背景噪声Love波成像
在获得Love波格林函数之后,用FTAN可以测量得到两台站间Love波的相速度和群速度. 群速度是描述一个波包即能量的行进速度.相速度描述的是不同周期的相位面传播速度.现代技术的发展使得可以同时测量相速度与群速度,这可以通过对一个解析信号进行窄带滤波之后进行FTAN(Frequency Time Domain Analysis)分析实现.解析信号是在频率域内舍去负频率部分,只保留正频率部分得到的(Bensen et al., 2007);在时间域内,解析信号的实部是原始信号,同时虚部是实部的Hilbert变换.为了提高时间序列的信噪比,相位匹配滤波(Phase Matched Filtering,PMF)(Levshin et al., 1992;Turin,1960;Herrin and Goforth, 1977);Goforth and Herrin, 1979)被用到FTAN中的Gabor矩阵上,从而得到更精确的群速度和相速度(Levshin et al., 1992).FTAN的工作原理是,用一系列窄带Gauss滤波器作用到待测量波形上得到一系列波包函数,分析这些波包就可以得到不同周期的群速度和相速度.至于为什么要选取Gauss函数类型的滤波器,主要是考虑到了不确定原理,只有Gauss函数能够保证时间域内的误差与频率域内的误差乘积最小(Dziewonski et al., 1969,1972).为了提高测量的精度,目前的FTAN技术还采纳了相位匹配滤波(Phase Matched Filter).关于已经发展成熟的FTAN技术的详细描述可以参考Levshin等(1992).
对FTAN分析得到的相速度和群速度结果还需要进行一次筛选,主要依据互相关函数的信噪比和台站间距(Bensen et al., 2007;Yang et al., 2011).Barmin等(2005)依据射线理论提出了区域甚至全球尺度的面波速度成像算法.对挑选过的相速度频散曲线进行层析成像得到秦岭及周边地区在不同周期范围内的Love波相速度分布.本研究计算了以下10个周期的Love波相速度分布:6 s,8 s,10 s,12 s,14 s,16 s,20 s,25 s,30 s.之所以选择相速度进行成像研究,是因为相速度的敏感度随深度的分布范围比群速度较深一些,因此,相对于群速度将会包含更深处的介质速度信息.层析成像划分的网格尺寸为0.5度乘以0.5度,将研究区在纬度方向划分为15个网格,经度方向划分为21个网格.
在周期为6 s的相速度分布图像中,秦岭造山带、六盘山和太行山南部都呈现出的是正的速度异常,反映了这些山脉地区浅部对应的速度较高的岩石地体和沉积层较薄甚至无沉积层覆盖.四川盆地和鄂尔多斯地块呈负异常,尤其鄂尔多斯东南部分以及渭河盆地是最大的负异常,这可能是由于四川盆地和鄂尔多斯地块上部覆盖较厚的低速沉积层导致,尤其渭河盆地的沉积层可能最厚.周期为8 s时,负异常主要集中在三个区域,鄂尔多斯块体西北部,鄂尔多斯东南部与秦岭交界的渭河盆地,以及四川盆地北部.Zheng 等(2010)利用背景噪声技术获得青藏高原东北部、鄂尔多斯块体以及四川盆地的Rayleigh波相速度分布,其结果同本研究结果类似,在8 s和12 s的相速度分布图中,鄂尔多斯块体、四川盆地以及渭河盆地都为低速异常.值得注意的是,四川盆地北部以及渭河盆地的这两个较强的负异常从8 s的图像一直延伸到20 s的图像,反映出在中上地壳,这两个地区都是相速度较慢的区域,这与其地质构造背景也是一致的.秦岭造山带的高速异常则是从8 s一直延伸到了20 s,其东部则延伸到25 s.在8 s到20 s的范围呢,本研究区所覆盖的鄂尔多斯南部并不是一个均匀一致的块体,西部一直是负异常,而东部则呈现正异常,可能是由于西部存在较厚的沉积层的影响.从8 s到20 s,在本研究区域的东边,有一条南北方向的高速异常带一直存在(沿着经度113°方向),并且这个异常带从北向南迁移,其南部边界从8 s时候的北纬33°向南迁移到了20 s的北纬32°,这是一个值得注意的观测结果. 2 三维SH波速度反演
面波速度是剪切波(S波)速度、P波速度和密度这三个参数的非线性函数(Bucher and Smith, 1971;Wildmer-Schnidrig and Laske, 2007),但对于剪切波速度的敏感度是最强的(Maceira,2009),而对P波速度和密度的敏感度已经被证明比剪切波小(Aki and Richards, 1980).在出现介质部分熔融的情况下,对于剪切波的速度影响比P波更大(Levshin et al., 1992),通过获取三维剪切波速度模型可以推断研究区的地壳和上地幔温度结构,所以获取秦岭地区的三维剪切波速度结构对于研究该区域地质构造演化十分重要.
在利用Love波相速度观测数据进行反演获得SH波速度结构的计算中,由于本研究的只得到了小于30s周期的Love波相速度分布,所以我们把研究的重心集中到60 km以上的地壳和上地幔结构.在深度方向60 km以内划分21个不同厚度的层,60 km以下采用的是均匀半无限空间地幔.其中,上地壳划分10层,中地壳划分6层,下地壳划分4层.反演迭代的初始速度输入模型为三维的crust 2.0模型(Bassin et al., 2000).反演的目标函数是使得正演计算的频散曲线与观测成像的频散曲线差的平方和最小(Julià et al., 2000;Maceira and Ammon, 2009),限制条件为SH波速度水平向二阶光滑,即Laplace平滑,对于地壳厚度也采用了二阶平滑约束.目标函数和限制条件用Lagrange乘子法转换为矩阵方程之后,用LSQR算法(Lawson et al., 1979;Paige and Saunders, 1982a,b)在阻尼最小二乘意义下求解.
虽然在反演计算中Moho面的深度是一个待求解的参数,但是在经过许多次迭代之后,相比于输入的三维模型crust 2.0,反演得到的Moho面变化很小,这是由于面波对于Moho界面的敏感度很小所以反演的界面深度并不会变化太大.由Love波反演得到的SH波速度与相速度的分布以及研究区地质构造特征是大体一致的.在6 km(图 6a)的时候,鄂尔多斯块体SH波速度较低,而且比较均匀,这是由于块体覆盖着厚厚的沉积层导致;同时还有渭河盆地以及四川盆地,同样是沉积层导致了较低的SH波速度;而秦岭东部则存在一片高速区域,这可能是由于高压超高压岩石被挤上来的结果.在深度为12 km(图 6b)附近,鄂尔多斯块体南部区域则比其北边的区域速度要高,再考虑到鄂尔多斯块体在20 km(图 6c)以及30 km(图 6e)的切片图,可以得出结论,鄂尔多斯块体的上地壳是不均匀的,南部速度较高,同时中下地壳是比较均匀的;而在地壳以下,也就是40 km(图 6e,f)以下,鄂尔多斯西南部分则呈现为高速区域.相比之下,渭河盆地的SH波速度模式则是另一种情形.在上地壳中,速度一直较低,这与沉积层较厚是相呼应的;在中下地壳并没有出现低速层,这个特征与北部的鄂尔多斯块体和南部的秦岭造山带完全不一样;而无论是在浅部还是深部,渭河盆地与四川盆地的SH波模式都十分一致.任隽等(2012)的人工地震结果显示,渭河盆地中上地壳为低速异常,同时下地壳为高速异常,而作为规模较大的陆内裂谷必然会引起地幔热物质主动或被动的上涌.在渭河盆地内部西安市附近,本文反演得到的SH波在深度40 km和50 km范围内显示了一个负速度异常.秦岭造山带东部上地壳比西部SH波速度要高,中下地壳东西较为一致,整个秦岭造山带在上地幔是负异常,低速带是否由于温度异常导致或者存在部分熔融体有待于进一步验证.
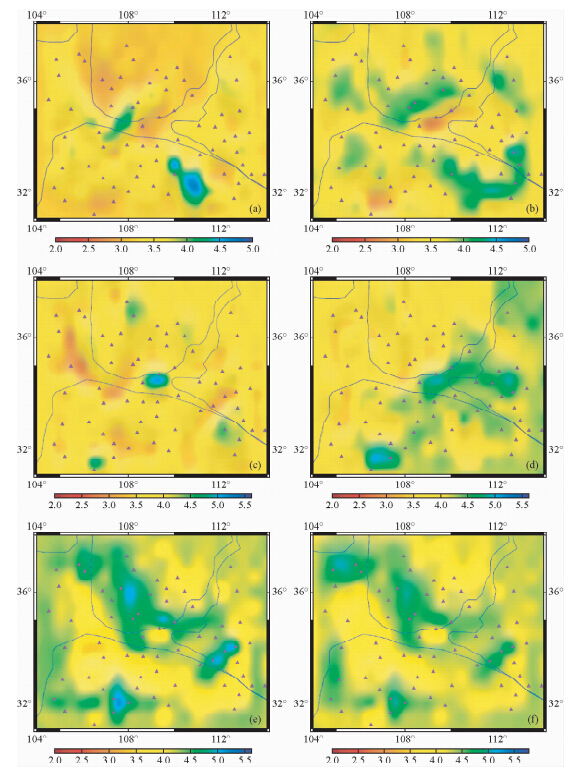 | 图 6 SH波速度在不同深度的反演结果Fig. 6 SH velocity at different depth |
为了便于进一步讨论,我们把研究区域划分为鄂尔多斯块体、秦岭造山带、四川盆地、渭河盆地4个子区域,并计算每个子区域的平均SH波速度随深度变化的曲线(图 7).从图中可以明显地看到,秦岭造山带的上地壳(5~15 km)的SH波速度明显高于其它3个子区域,可能是反映了秦岭造山带由于长时间的地表剥蚀导致了地壳的整体抬升,把原来的下地壳部分(Vsh=3.6~3.8 km/s)抬升到了现在的上地壳位置.更重要的是,秦岭造山带Moho面下面(40~50 km)存在一个较强的低速带.
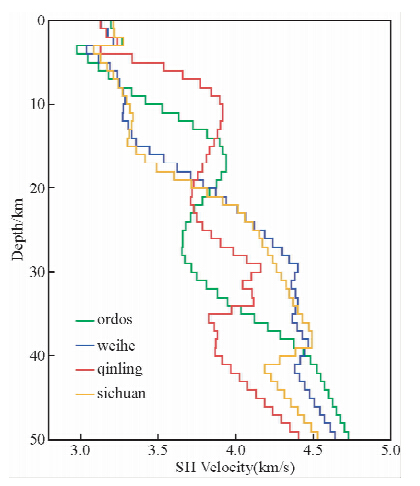 | 图 7 鄂尔多斯块体、秦岭造山带、四川盆地、渭河盆地4个子区域的一维SH波平均速度反演结果Fig. 7 Inverted average 1D SH velocity distribution of the 4 sub-areas |
本文将背景噪声技术应用于北京大学与中国地质科学院合作在秦岭及周边地区布设的流动地震台阵观测记录,提取了台站间Love波频散曲线进行Love波相速度层析成像,获得了台阵所覆盖的研究区域(包括鄂尔多斯南部和秦岭造山带)的Love波相速度分布图像,进一步反演获得研究区下SH波三维速度结构.
无论是Love波相速度分布图,还是SH波分布图都显示出鄂尔多斯块体南部并不是一个均匀的整体,西边相速度比东边的慢,沉积层并不是对称的,西边厚东边薄.鄂尔多斯块体浅层结构与深层结构不一致,中地壳的SH波速度比上地壳和下地壳都高,Moho面以下为高速异常.渭河盆地和四川盆地北部地区上地壳呈现较强的低速异常,揭示这些盆地具有较厚的沉积层.
SH波反演结果显示在6~8 km深度范围,秦岭东部比秦岭西部的速度要高.这一结果支持地质学研究的观点,秦岭海自晚二叠世开始到晚三叠世结束向西关闭,东部的海相沉积岩比西部的更古老(Seguin和翟永建,1995).SH波在50 km深度处的速度分布显示秦岭造山带东部速度高,其原因是地壳厚度高度收缩、消减与抬升,东部有可能是由于拆沉作用而导致地壳减薄且无山根,西部较东部年轻,有残留的山根,高山等(1999)综合了地质、地球物理和地球化学的证据,从地质构造,地壳厚度以及元素分布方面论证了秦岭地区下地壳拆沉机制(张国伟等,1995;高山等,1999).最后,SH波速度在50 km深度的分布图像显示,秦岭造山带以及鄂尔多斯块体外部西北方向呈现较强的低速异常,这个连贯的低速异常带是否是由于温度异常导致或者存在部分熔融体还有待于进一步验证.一种解释是青藏高原上地幔物质向东扩展遇到鄂尔多斯块体和四川盆地块体的阻挡,只能够在这两个块体之间的秦岭造山带下面向东扩展流动,从而导致了本文图 6d显示的秦岭造山带Moho面下(50 km)的连贯的低速异常带,另外,这个模式也可以解释为什么秦岭造山带无“山根”的观测结果.
致 谢 作者十分感谢梁晓峰博士的建议.本研究是北京大学与中国地质科学院合作研究的一部分工作,获得了中国地质科学院工作项目为《中央造山带与南北构造带交汇区地壳深部地质调查》资助.作者对于北京大学和中国地质科学院地质力学研究所安美健研究小组参加野外流动地震台阵布设和数据采集的全体师生表示感谢.| [1] | Aki K. 1957. Space and time spectra of stationary stochastic waves, with special reference to microtremors[J]. Bull. Earthquake-Res. Inst. Tokyo, 35(3): 415-456. |
| [2] | Aki K, Richards P G. 1980. Quantitative Seismology[M]. San Francisco: Freeman. |
| [3] | Baig A M, Campillo M, Brenguier F. 2009. Denoising seismic noise cross correlations[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 114(B8), doi: 10.1029/2008JB006085. |
| [4] | Barmin M P, Ritzwoller M H, Levshin A L. 2001. A fast and reliable method for surface wave tomography[A].//Levshin A L, Ritzwoller M H eds. Monitoring the Comprehensive Nuclear-Test-Ban Treaty: Surface Waves[M]. Basel: Birkhuser Verlag, 1351-1375. |
| [5] | Bassin C, Laske G, Masters G. 2000. The current limits of resolution for surface wave tomography in North America[J]. Eos, 81. |
| [6] | Bensen G D, Ritzwoller M H, Barmin M P, et al. 2007. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophysical Journal International, 169(3): 1239-1260. |
| [7] | Bensen G D, Ritzwoller M H, Shapiro N M. 2008. Broadband ambient noise surface wave tomography across the United States[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 113(B5), doi: 10.1029/2007JB005248. |
| [8] | Bucher R L, Smith R B. 1971. Crustal structure of the eastern basin and range province and the northern Colorado Plateau from phase velocities of rayleigh waves[A].//Heacock J G ed. The Structure and Physical Properties of the Earth's Crust[M]. Washington, DC: American Geophysical Union, 59-70. |
| [9] | Campillo M, Paul A. 2003. Long-range correlations in the diffuse seismic coda[J]. Science, 299(5606): 547-549. |
| [10] | Dziewonski A, Bloch S, Landisman M. 1969. A technique for the analysis of transient seismic signals[J]. Bulletin of the Seismological Society of America, 59(1): 427-444. |
| [11] | Dziewonski A, Mills J, Bloch S. 1972. Residual dispersion measurement—a new method of surface-wave analysis[J]. Bulletin of the Seismological Society of America, 62(1): 129-139. |
| [12] | Gao S, Zhang B R, Jin Z M, et al. 1999. Lower crustal delamination in the Qinling-Dabie orogenic belt[J]. Science in China (Series D) (in Chinese), 42 (4): 423-433. |
| [13] | Goforth T, Herrin E. 1979. Phase-matched filters: application to the study of Love waves[J]. Bulletin of the Seismological Society of America, 69(1): 27-44. |
| [14] | Gorbatov A, Saygin E, Kennett B L N. 2013. Crustal properties from seismic station autocorrelograms[J]. Geophysical Journal International, 192(2): 861-870. |
| [15] | He J K, Liu F T, Liu J H, et al. 1998. The morpholocy of moho discontinuity and it's evolution geodynamics in the eastern Qinling collisional orogenic belt[J]. Acta Geophysica Sinica (in Chinese), 41(S1): 64-76. |
| [16] | Herrin E, Goforth T. 1977. Phase-matched filters: application to the study of Rayleigh waves[J]. Bulletin of the Seismological Society of America, 67(5): 1259-1275. |
| [17] | Julià J, Ammon C J, Herrmann R B, et al. 2000. Joint inversion of receiver function and surface wave dispersion observations[J]. Geophysical Journal International, 143(1): 99-112. |
| [18] | Kimman W P. 2011. Higher mode surface wave interferometry[J]. Geologica Ultraiectina, 336. |
| [19] | Lawson C L, Hanson R J, Kincaid D R, et al. 1979. Basic linear algebra subprograms for Fortran usage[J]. ACM Transactions on Mathematical Software (TOMS), 5(3): 308-323. |
| [20] | Levshin A, Ratnikova L, Berger J. 1992. Peculiarities of surface-wave propagation across central Eurasia[J]. Bulletin of the Seismological Society of America, 82(6): 2464-2493. |
| [21] | Li H Y, Bernardi F, Michelini A. 2010a. Love wave tomography in Italy from seismic ambient noise[J]. Earthquake Science, 23(5): 487-495. |
| [22] | Li H Y, Su W, Wang C Y, et al. 2010b. Ambient noise Love wave tomography in the eastern margin of the Tibetan plateau[J]. Tectonophysics, 491(1-4): 194-204. |
| [23] | Lin F C, Moschetti M P, Ritzwoller M H. 2008. Surface wave tomography of the western United States from ambient seismic noise: Rayleigh and Love wave phase velocity maps[J]. Geophysical Journal International, 173(1): 281-298. |
| [24] | Lobkis O I, Weaver R L. 2001. On the emergence of the Green's function in the correlations of a diffuse field[J]. The Journal of the Acoustical Society of America, 110: 3011. |
| [25] | Maceira M, Ammon C J. 2009. Joint inversion of surface wave velocity and gravity observations and its application to central Asian basins shear velocity structure[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 114(B2), doi: 10.1029/2007JB005157. |
| [26] | Paige C C, Saunders M A. 1982a. LSQR: An algorithm for sparse linear equations and sparse least squares[J]. ACM Transactions on Mathematical Software (TOMS), 8(1): 43-71. |
| [27] | Paige C C, Saunders M A. 1982b. Algorithm 583: LSQR: Sparse linear equations and least squares problems[J]. ACM Transactions on Mathematical Software (TOMS), 8(2): 195-209. |
| [28] | Paul A, Campillo M, Margerin L, et al. 2005. Empirical synthesis of time-asymmetrical Green functions from the correlation of coda waves[J]. Journal of Geophysical Research, 110(B8): B08302, doi: 10.1029/2004JB003521. |
| [29] | Poli P, Campillo M, Pedersen H, et al. 2012. Body-wave imaging of earth's mantle discontinuities from ambient seismic noise[J]. Science, 338(6110): 1063-1065. |
| [30] | Prieto G A, Beroza G C. 2008. Earthquake ground motion prediction using the ambient seismic field[J]. Geophysical Research Letters, 35(14): L14304, doi: 10.1029/2008GL034428. |
| [31] | Prieto G A. 2012. Imaging the deep earth[J]. Science, 338(6110): 1037-1038. |
| [32] | Schimmel M, Paulssen H. 1997. Noise reduction and detection of weak, coherent signals through phase-weighted stacks[J]. Geophysical Journal International, 130(2): 497-505. |
| [33] | Seguin M K, Zhai Y J. 1995. Paleomagnetic constraints on the convergence of the Sino-Korean and Yangtze blocks, China[J]. Acta Geohysica Sinica (in Chinese), 38(1): 34-45. |
| [34] | Shapiro N M, Campillo M. 2004. Emergence of broadband Rayleigh waves from correlations of the ambient seismic noise[J]. Geophysical Research Letters, 31(7), doi: 10.1029/2004GL019491. |
| [35] | Shapiro N M, Campillo M, Stehly L, et al. 2005. High-resolution surface-wave tomography from ambient seismic noise[J]. Science, 307(5715): 1615-1618. |
| [36] | Stehly L, Fry B, Campillo M N, et al. 2009. Tomography of the Alpine region from observations of seismic ambient noise[J]. Geophysical Journal International, 178(1): 338-350. |
| [37] | Tang, Y C, Chen Y J, Zhou et al. 2013. Lithosphere structure and thickness beneath the North China Craton from Joint inversion of ambient noise and surface wave tomography[J]. J. Geophys. Res., 118(5), doi: 10.1002/jgrb.50191. |
| [38] | Teng J W, Yan Y F, Wang G J, et al. 2006. Structure of Earth's crust and upper mantle, inland subduction and its coupling effects on the Dabie orogenic belt and the Tancheng-Lujiang fault zone[J]. Chinese J. Geophys. (in Chinese), 49(2): 449-457. |
| [39] | Turin G. 1960. An introduction to matched filters[J]. IRE Transactions on Information Theory, 6(3): 311-329. |
| [40] | Weaver R L, Lobkis O I. 2001. Ultrasonics without a source: Thermal fluctuation correlations at MHz frequencies[J]. Physical Review Letters, 87(13): 134301. |
| [41] | Widmer-Schnidrig R, Laske G. 2007. 1.03-Theory and observations-normal modes and surface wave measurements[J]. Treatise on Geophysics, 1: 67-125. |
| [42] | Yang Y J, Shen W S, Ritzwoller M H. 2011. Surface wave tomography on a large-scale seismic array combining ambient noise and teleseismic earthquake data[J]. Earthquake Science, 24(1): 55-64. |
| [43] | Yuan X C, Xu C M, Tang W B, et al. 1994. Eastern Qinling seismic reflection profiling[J]. Acta Geophysica Sinica (in Chinese), 37(6): 749-758. |
| [44] | Zhang G W, Meng Q R, Lai S C. 1995. Tectonics and structure of Qinling orogenic belt[J]. Science in China (Series B) (in Chinese), 38(11): 1379-1394. |
| [45] | Zheng Y, Yang Y J, Ritzwoller M H, et al. 2010. Crustal structure of the northeastern Tibetan plateau, the Ordos block and the Sichuan basin from ambient noise tomography[J]. Earthquake Science, 23(5): 465-476. |
| [46] | 高山, 张本仁, 金振民,等. 1999. 秦岭-大别造山带下的地壳拆沉作用[J]. 中国科学(D 辑), 29(6): 532-541. |
| [47] | 何建坤, 刘福田, 刘建华,等. 1998. 东秦岭造山带莫霍面展布与碰撞造山带深部过程的关系[J]. 地球物理学报, 41(增刊): 64-76. |
| [48] | Seguin M K, 翟永建. 1995. 中朝陆块与扬子陆块会聚的古地磁证据[J]. 地球物理学报, 38(1): 34-45. |
| [49] | 滕吉文, 闫雅芬, 王光杰,等. 2006. 大别造山带与郯庐断裂带壳、幔结构和陆内“俯冲”的耦合效应[J]. 地球物理学报, 49(2): 449-457. |
| [50] | 袁学诚, 徐明才, 唐文榜,等. 1994. 东秦岭陆壳反射地震剖面[J]. 地球物理学报, 37(6): 749-758. |
| [51] | 张国伟, 孟庆任, 赖绍聪. 1995. 秦岭造山带的结构构造[J]. 中国科学(B 辑), 25(9): 994-1003. |
 2015, Vol. 30
2015, Vol. 30


