麦克斯韦(James Clerk Maxwell)理论认为,磁铁运动产生电场,而导体运动不产生电场;但爱因斯坦却认为,当一个导体和磁铁相对运动时,在导体里产生的电流并不取决于两者哪个在运动.洛伦兹(Hendrik Antoon Lorentz)认为,力学处于一个优越的地位,而电动力学是从属的;但爱因斯坦却认为,力学与电动力学是平权的,力学和电磁学必须服从共同的原则.于是爱因斯坦指出:不能给予同时性这个概念以任何绝对的意义,两个事件,从一个坐标系看来是同时的,而从另一个相对于这个坐标系运动的坐标系来看,就不能再被认为是同时的事件了.基于这个思想,爱因斯坦提出了狭义相对论的“相对性原理”:凡是对力学方程适用的一切坐标系,对电动力学和光学也一样适用.爱因斯坦同时坚持“相对性原理”和“光速不变”,从而得出了狭义相对论的“速度延缓时间原理”,即:速度越快、时间越慢.
狭义相对论还不完善,不能处理加速度和引力现象.创立狭义相对论之后,爱因斯坦基于把“相对性原理”贯彻到底的信念和认识论的原则,一鼓作气又创立了广义相对论.
牛顿力学认为:惯性系比其它坐标系都要特殊,且速度是相对的而加速度是绝对的.对此,爱因斯坦不以为然.因为伽利略早就发现:一切物体在引力场中都具有同一加速度,即物体的惯性质量同它的引力质量相等.爱因斯坦从这一事实想到了“等效原理”.等效原理也称为“广义相对性原理”,爱因斯坦在这里把狭义相对论的“相对性原理”推广到了加速系:如果在一个引力场里不是引进一个惯性系,而是引进一个相对于它作加速运动的参考系,那么事物就会像在没有引力的空间里那样行动.根据“等效原理”,爱因斯坦得出了广义相对论的“引力延缓时间原理”,即:引力越大、时间越慢.
2 我国学者不久前的工作
狭义相对论以光速为尺度,认为速度越快时间越慢;而广义相对论以引力为尺度,认为引力越大时间越慢.所以总的来说,“引力问题”不是狭义相对论问题而是广义相对论问题.但是,也有学者试图把狭义相对论的尺度和广义相对论的尺度统一起来、也就是把光速和引力速度统一起来,提出了引力速度等于光速的观点(Ohanianet al.,1976; Hartle J B,2008).
不久前,汤克云研究员等发表论文(Tanget al.,2013),认为从重力固体潮的观测资料中证实了引力速度等于光速.随后,黄超光研究员发表论文(Huang,2013),认为汤克云的重力固体潮观测分析与引力速度无关.
实际上,采用重力测量的方法探测引力速度是很困难的.为了探测引力波,马里兰大学的Joseph Weber教授于1959年发明了室温下工作的谐振质量引力波探测器,Ho Jung Paik教授根据其发现的谐振传感器的概念,采用低温超导技术,设计了双模超导传感器去实现引力波探测、并设计了超导重力梯度仪,但是并没有在引力波探测方面取得成功.意大利物理学家Majorana关于重力吸引的实验和假说(Liuet al.,2004),引起了在日全食期间探测引力波的研究.1997年3月,王谦身等在漠河日全食期间利用高精度重力仪实施了观测,发现了“重力谷”现象(王谦身等,2001).2009年7月,方剑等在长江日全食期间利用高精度重力仪实施了观测,但并未发现“重力谷”现象(崔荣花等,2011).
目前,重力测量的精度为10-6至10-7量级,而时间测量的精度则已达到了10-12量级,所以时间测量精度比重力测量精度要高得多;另外,重力测量受外界干扰较大(如海潮、大气、地下水等),而时间测量干扰较小.也就是说,从观测精度上来说,走时间测量的技术路线应该比走重力测量的技术路线更为现实.因此,与汤克云研究员基于日月引力的“重力固体潮实验方案”不同,我们提出基于地球引力的“GPS卫星实验方案”. 3 GPS卫星相对论效应的影响
3.1 狭义相对论效应的影响
根据狭义相对论的“速度延缓时间原理”:速度越快、时间越慢.在地面上具有频率为f0的时钟,安设在以速度Vs运行的卫星上后,钟频将发生变化,其改变量为(因为卫星相对地球运行速度很快,所以卫星上的时钟将变慢)(周忠谟等,1999):
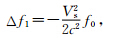
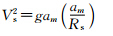
所以
根据广义相对论的“引力延缓时间原理”:引力越大、时间越慢.于是,处于不同等位面的时钟,其频率f0将由于引力位不同而产生变化,这种引力频移的量的大小为(因为卫星相对地球很远、引力很小,所以卫星上的时钟将变快)(周忠谟等,1999):
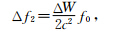
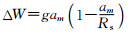
所以
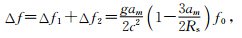
将以上频率影响Δf换算成时间影响Δt:
所以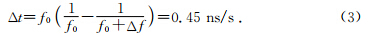
这就是说,受狭义相对论和广义相对论的合并影响,GPS卫星钟比地面钟要快0.45 ns/s,也就是38 μs/d;其中:广义相对论效应影响为45 μs/d,狭义相对论效应影响为-7 μs/d.如果按照1纳秒误差对应的定位精度为0.3 m,那么广义相对论的45 μs/d的误差影响所对应的定位精度为
45×1000×0.3=13500 m/d = 13.5 km/d
4 基于地球引力的“GPS卫星实验方案”GPS卫星的平均高度为20200 km(光速约需要1/15 s),月亮到地球的距离约38万km(光速需1秒多),太阳到地球的距离约1.5亿km(光速约需500秒).目前GPS的观测精度为毫米级,GPS卫星钟的精度为纳秒(10-9)级.我们的“GPS卫星实验方案”的技术思路是:采用时间测量的方法,验证GPS卫星受地球引力的广义相对论效应(45μs/d),是否受到1/15s延迟的影响,以此来验证引力按光速传播.具体方案如下:
设在地球表面上一台GPS接收机为A,空间一颗GPS卫星为B,设引力速度为u,u=αc(c为光速,α≦1为比例系数).
那么,由A点时刻归算到地心时刻为
所以
所以
所以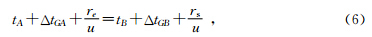
所以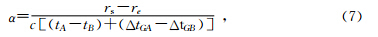
也就是说,在(7)式中,(rs-re)和(tA-tB)为可观测量.(tA-tB)为时间观测量,而(rs-re)也可以换算成时间观测量.
于是,由(tA-tB)和(rs-re)这两个时间观测量,就可以由公式(7)计算出比例系数α,从而进行引力速度等于光速的验证;如果计算出的比例系数α接近1,则可认为引力速度等于光速.
| [1] | Hartle J B. 2008. Gravity: An Introduction to Einstein's General Relativity[M]. San Francisco: Addison Wesley. |
| [2] | Ohanian H C. 1976. Gravitation and Spacetime[M]. New York: W. W. Norton & Company, Inc. Tang K Y, Hua C C, Wen W, et al. 2013. Observational evidences for the speed of the gravity based on the Earth tide[J]. Chin Sci Bull, 58: 474-477. |
| [3] | Huang C G. 2013. The observation of the Earth tide is irrelevant to the speed of gravity[J]. Chin Sci Bull, 58: 3291-3294. |
| [4] | Liu Shaoming, van Ruymbeke M. 2004. Search for Gravitational Absorption Effect During Total Solar Eclipse of August 11, 1999 [J]. Journal of Geodesy and Geodynamics, 25(4): 99-104. |
| [5] | Wang Qianshen, Yang Xinshe, Tang Keyun. 2001. Gravity anomaly during the Mohe total solar eclipse[J]. Chin Sci Bull (in Chinese), 46(12): 1044-1048. |
| [6] | Cui Ronghua, Fang Jian, Wang Xinsheng. 2011. Gravity Observation During 22 July 2009 Total Solar Eclipse in Hubei Province[J]. Geomatics and Information Science of Wuhan University (in Chinese), 36(11): 1332-1335. |
| [7] | Zhou Zhongmo, Yi Jiejun, Zhou Qi. 1999. The principle and application of the GPS satellite measurement[M]. Beijing: Surveying and Mapping Press (in Chinese) . |
| [8] | 汤克云,华昌才,文武,等.2013. 由固体潮发现引力以光速传播的观测证据[J]. 科学通报,58:907-911. |
| [9] | 王谦身,杨新社,汤克云.2001. 漠河日全食期间的重力异常[J].科学通报,46(12):1044-1048. |
| [10] | 崔荣花,方剑,王新胜. 2011. 2009-07-22湖北地区日全食期间的重力观测[J]. 武汉大学学报(信息科学版),36(11):1332-1335. |
| [11] | 周忠谟,易杰军,周琪.1999. GPS卫星测量原理与应用[M].北京:测绘出版社. |
 2014, Vol. 29
2014, Vol. 29

