2. 辽宁工程技术大学计算力学研究所, 阜新 123000
2. Institute of Computational Mechanics, Liaoning Technical University, Fuxin 123000, China
雁列构造是一种野外常见的非连续地质构造.拉张型和挤压型是两类常见且重要的雁列构造.地震界、地质界等领域的众多科技人员开展了大量的与雁列构造有关的研究工作(Segall and Pollard, 1980;Sibson,1985;Ma et al., 1986,2010;Aydin and Schultz, 1990;Swanson,1990;Thomas and Pollard, 1993;Zachariasen and Sieh, 1995;Talwani,1999; de Joussineau et al., 2003;Barker,2005;Smith and Yamauchi, 2005;Soliva et al., 2010).一些关于断层相互作用、地震机理、前兆及过程的研究也常以雁列构造为例进行分析和讨论(Sibson,1985;刘力强等,1986;Ma et al., 1986,2010;马文涛等,1995;马胜利等, 1995a,1995b,2004,2008;马瑾等, 1999,2002,2007,2008;蒋海昆等,2002;刘培洵等,2007;任雅琼等,2013).目前,关于雁列构造的研究主要集中在理论分析、实验研究、野外观测及统计等方面.相比之下,数值模拟方面的研究成果少见(Aydin and Schultz, 1990;Olson and Pollard, 1991;Du and Aydin, 1995;Harris and Day, 1999; de Joussineau et al., 2003;Ohlmacher and Berendsen,2005;Palusznya and Matth ib,2009).随着计算机软、硬件水平的不断发展,数值方法在上述问题研究中可望能发挥越来越重要的作用.采用合适的数值模型,开展实验室尺度模型的研究工作,是实验研究的有力补充,并能积极促进或推动有关的研究向前发展,极大地增进人们对于断层相互作用及失稳前兆的认识和理解.在数值模拟之中,一些费时费力甚至难于在当前技术条件下实现的实验方案,可能方便地实现;一些困扰实验研究的难题可以方便地被克服或避免,例如,试验机压头之间的干涉,多种观测元件之间的干扰,高围压、水压的施加,同批次标本之间或多或少存在差异,声发射监测中的“死时间”问题,观测区域受限或观测变量受限等问题.
过去针对雁列构造的数值模拟研究,多针对应力场、应变场、位移场及动态断裂过程等进行分析,考察的力学量有限.在一些数值模型之中,不允许单元破坏,因而难于研究雁列区的贯通过程及引起的多种力学量的变化规律;少见非均质性被引入.事实上,材料或几何非均质性的重要性怎么强调也不过分.在连续介质模型之中引入某种程度上的非均质性,即可模拟地震的时空复杂形为(Miyatake,1992;Beroza and Mikumo, 1996;Bizzarri et al., 2001;Hillers et al., 2006).
近年来,作者开展了典型断层构造破裂失稳前兆及粘滑过程的数值模拟研究(Wang et al., 2010,2012,2013a,2013b;王学滨等, 2013,2014).考虑到上述问题研究的难度,将上述问题分别对待,采用两种模型分别进行分析和讨论.
在第1种模型中,分别考虑了断层和岩石的非均质性,针对雁列构造及Z字型构造开展研究.这种模型适于模拟一个粘滑周期内断层系统的复杂力学行为.研究发现,挤压雁列区贯通过程中b0值(事件的频次-能量释放关系的斜率的绝对值)表现为下降(Wang et al., 2010),而对于拉张雁列构造则观察不到b0值的明显变化(Wang et al., 2010,2012).在挤压雁列区贯通过程中,与剪切应变降有关的量的表现比较突出,这是由于1个单元的破坏,能引起周围众多单元剪切应变的降低,即弹性卸载(Wang et al., 2013b).
在第2种模型中,未考虑非均质性,断层系统由断层和之外的破坏区(针对雁列构造而言)以及弹性岩石构成.对于断层单元,在应变软化之后考虑了应变硬化,以模拟随着断层滑动距离的增加,断层面的强度愈合现象.采用这种模型,模拟了单一、交叉、拐折及雁列构造的粘滑过程.针对拐折构造的计算发现,大粘滑事件与断层不同段落的同步失稳有关,而小粘滑事件与不同区段的非同步失稳有关(Wang et al., 2013a).
为了探索事件的迁移及前兆规律,本文以拉张型雁列构造为例进行数值分析和讨论.数值计算在FLAC-3D软件中实现,采用了提出的非均质应变软化模型(Wang et al., 2010,2012,2013b).为了研究两条断层的相互影响和作用,在两条断层的内、外侧岩石上布置了若干被监测单元,监测它们的剪切应变的演变规律.在标本全场内对大于某一临界值的剪切应变降进行了捕捉,并对与此有关的3种量进行了统计.文中还阐明了雁列区内的破坏区不启动于断层端部现象的原因.1 计算模型及主要参数
图 1中岩石标本包含两条具有一定重叠量的平行断层,在重叠区域构成雁列构造.断层的重叠量和间距相等,均为0.0184 m.在纸面内,标本的形状为正方形,边长为0.3 m,被剖分成9万个尺寸相同的单元.两条断层与水平方向的夹角均为45°.
在平面应变条件下进行计算,仅允许单元发生小变形.计算过程包括两个阶段:
首先,在静水压力(σ1=σ3=-2 MPa)条件下,将标本加载至静力平衡状态.这一阶段消耗2万个时步.若标本中节点的最大不平衡力已经足够小则意味着标本已经达到静力平衡状态.一个时步是指一次计算循环,从运动方程经由几何方程,到本构方程,再到运动方程.循环一次,则时步数目增加1.
其次,在标本左、右两端进行压缩的位移控制加载,加载速度v=1×10-9 m/时步,而标本上、下两端的压应力与第1阶段相同.通过计算标本左、右两端上各节点不平衡力的合力与这两端的几何尺寸的商得到这两端的压应力.计算发现,该压应力的值大于标本上、下两端的压应力的值(2 MPa),所以应为σ1.由于两断层端部连线方向与σ1垂直,所以图 1中的雁列构造为拉张型.
标本中包含两种单元:岩石单元和断层单元.这两种单元的本构模型相同,但有些参数的取值不同.在弹性阶段,两种单元均服从各向同性的线弹性模型;在破坏阶段,两种单元均服从带拉伸截断的应变软化莫尔-库仑模型.
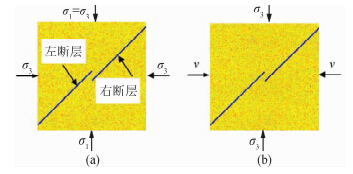 | 图 1 拉张雁列构造的计算模型(a)静水压力加载阶段;(b)水平方向位移控制加载阶段.Fig. 1 A computational model for the extensional echelon fault(a)The initial loading stage;(b)Horizontal displacement-controlled loading stage. |
为了延缓单元的破坏过程,增加发现前兆的可能性,我们对传统的均质模型进行了改进(Wang et al., 2010,2012,2013b),假定一些材料参数在空间上呈不均匀分布,即弹性模量、初始粘聚力和抗拉强度在标本内部服从Weibull分布,非均质性参数取值适中,即m=9,且它们彼此之间不相关.其余参数被认为是均匀的,例如泊松比、初始内摩擦角等.
对于岩石单元和断层单元,弹性模量的均值分别取为55 GPa和5.1 GPa;泊松比分别取为0.25和0.2;初始粘聚力的均值分别取为37.5 MPa和5 MPa;抗拉强度的均值分别取为24 MPa和1.2 MPa;初始内摩擦角分别取为50°和10°,扩容角均取为0°.
为了模拟应变软化,除了需要规定强度参数的初始值,还需规定软化阶段结束时的残余强度参数和所对应的塑性剪切或拉伸应变的值.我们假定,随着单元塑性变形的增加,单元的强度参数倾向于相同.也就是说,具有不同初始强度参数的单元的残余强度参数及所对应的塑性应变相同.这也意味着,强度参数越高的单元的峰后脆性越强.
上述参数的具体取值及依据参见Wang等(2010,2012,2013b). 2 计算结果分析
2.1 破坏区分布
图 2给出了雁列区贯通过程及之前不同时步数时标本中破坏单元的分布规律.黑色单元代表已发生剪切或拉伸破坏的单元.
由图 2可以发现,随着时步数的增加(或σ1方向线应变的增加),破坏单元由远离雁列区的断层上逐渐向雁列区迁移,直至雁列区贯通.
在4.8万个时步数之前(图 2a~c),雁列区内尚未出现破坏单元.当时步数达到4.9万个时(图 2d),在右断层某一位置(过左断层端部且垂直于两条断层的直线与右断层的交点处)扩展出了破坏区.当时步数达到5.0万个时(图 2e),扩展出的破坏区已接近左断层端部.当时步数达到5.1万个时(图 2f),雁列区已被上述破坏区贯通,与此同时,在左断层某一位置(过右断层端部且垂直于两条断层的直线与左断层的交点处)也扩展出了破坏区.随后,这条破坏区也将贯通雁列区.
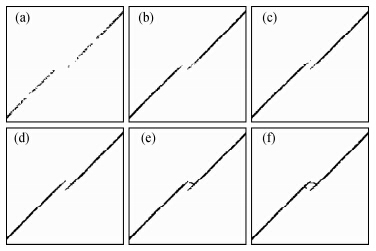 | 图 2 不同时步数时破坏单元的分布(a~f)时步数分别为4.1万、4.6万、4.8万、4.9万、5.0万及5.1万.Fig. 2 Distributions of failed elements for different timestep numbers(a~f)The timestep number is 4.1×104,4.6×104,4.8×104,4.9×104,5.0×104 and 5.1×104,respectively.. |
上述破坏区不启动于断层端部,而启动于断层某一位置的现象似乎有些反常.显然,对于标本中仅有一条断层的情形而言,这种现象不应出现.在实验室及野外,也能观察到上述反常现象(图 3).在图 3a中,拉张雁列区内部的裂纹不启动于两条断层的任一端;在图 3b中,大量声发射事件集中于下方断层的某一位置,预示着这一位置的开裂;在图 3c中,两条断层之间的新断裂启动于下方断层的某一位置.据此推测,上述反常现象的出现应与两条断层之间的相互影响和作用有关.
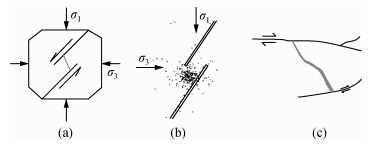 | 图 3 实验室及野外发现的反常裂纹启裂位置(a)陈顺云等(2005);(b)马胜利等(2008);(c)Sibson(1985).Fig. 3 Abnormal crack initiation positions observed in experiments and in situ(a)Chen et al.(2005);(b)Ma et al.(2008);(c)Sibson(1985). |
为了揭示上述反常现象的原因,我们给出了一条反常裂纹启动前后雁列区附近的速度场(图 4).标本在水平方向压缩条件下,右断层下盘的岩石主动地向左运动,而上盘岩石被动地斜向上(或垂直于右断层方向)运动.随着时步数的增加,向上运动的岩石尺寸越来越大,其前锋越来越向雁列区逼近.由于拉张雁列区之内的应力是以拉应力为主,当其前锋抵达拉张雁列区的边缘时,过高的拉应力将使前锋处的岩石单元发生拉破坏,进而诱发出垂直于右断层方向的拉裂纹.
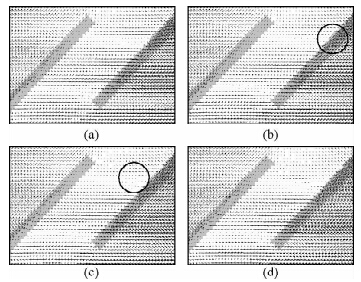 | 图 4 反常裂纹启裂前后雁列区附近的速度场(a~d)时步数分别为4.8万、4.85万、4.9万和4.95万;圆圈位置表示斜向上运动的岩石的前锋. Fig. 4 Velocity fields prior to the abnormal crack initiation and beyond(a~f)The timestep number is 4.8×104,4.85×104,4.9×104 and 4.95×104,respectively. |
在FLAC-3D中,剪切应变增量定义为

为了获得标本中特定位置剪切应变的演变规律,在两条断层的内、外侧均布置了一些被监测单元(图 5).在某条断层的任一侧,被监测单元的连线平行于该断层,且被监测单元等间隔布置.被监测单元均布置在岩石单元上.左断层内侧、外侧、右断层内侧、外侧的被监测单元编号分别为3~32、33~62、63~92及93~122.值得指出的是,有一些被监测单元布置在断层端部的前方,例如,被监测单元3~8等.
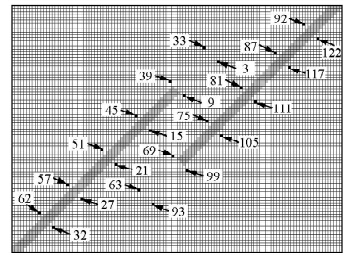 | 图 5 部分被监测单元布置Fig. 5 Arrangement of a part of monitored elements |
图 6给出了左断层内侧(包括断层端部前方)的多个被监测单元的剪切应变随时步数的演变规律,同时,也给出了标本左、右端面的σ1的值随时步数的演变规律(标记为1的曲线).红色箭头指明了雁列区贯通的时刻.由此可以发现:
(1)在雁列区贯通之前及之后,σ1的值总体上呈现上升的态势,但前、后上升速度不同.在大约4.5万个时步数之前,σ1的值上升较快,但此后,σ1的值上升放慢.这与马胜利等(2008)的实验结果(差应力随时间增加的速度明显减缓)基本一致,雁列区的贯通难于在σ1的演变规律中找到明显的标志,但却引起了某些位置被监测单元剪切应变的快速下降,例如被监测单元9、12及15,它们均位于雁列区内部,这与这些单元附近发生破坏有关.马胜利等(2008)通过实验也发现,靠近雁列区的应变释放极为明显.反之,对于被监测单元3及7,由于附近没有破坏单元,所以在雁列区贯通过程中,没有观察到剪切应变快速下降现象.
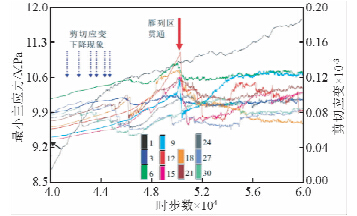 | 图 6 最小主应力(σ1)及左断层内侧被监测单元的剪切应变随时步数的演变规律Fig. 6 Evolution of the minor principal stress(σ1) and shear strains of monitored elements at the inner side of the left fault with timestep number |
(2)在雁列区贯通之前及之后,被监测单元的剪切应变的演变规律有重大的差别.在雁列区贯通之前,可以观察到一些被监测单元的剪切应变的缓慢上升和快速下降现象,这样的现象重复了多次(图 6中蓝色虚箭头),就像粘滑一样;离雁列区越远,剪切应变下降现象出现得越早;在雁列区贯通之后,仅观察到了剪切应变的小幅度震荡现象.马胜利等(2008)通过实验发现,在雁列区贯通之前,断层内侧各点应变在随时间缓慢增加的背景上伴有准周期性的台阶式下降.这与本文的上述结果基本类似.
图 7a~b给出了左、右断层内侧被监测单元的剪切应变的演变规律.由此可以发现下列现象:
(1)在虚线1及1′的位置,剪切应变降仅发生在左断层内侧,例如,第23、25号被监测单元.
(2)在虚线2及2′的位置,剪切应变降同时发生在两条断层内侧,例如,第23、89号被监测单元.
(3)在虚线3及3′的位置,剪切应变降仅发生在右断层内侧,例如,第79号被监测单元.
(4)在虚线4及4′的位置,剪切应变降先发生在左断层内侧,后发生在右断层内侧,例如,第25、79号被监测单元.
(5)在虚线5及5′的位置,剪切应变先发生降低(在左断层内侧),然后发生突增(在右断层内侧),例如,第27号和第87号被监测单元.
至少,部分现象(左、右断层内侧剪切应变降同时发生等)应该根源于断层之间的相互影响和作用.两条断层附近的剪切应变的演变规律非常复杂,同步、不同步共存.马瑾等(2002)从剪应力的角度分析了断层相互作用引起的促震和减震效应.从本文的结果看,断层之间的相互作用对于有的部位产生了减震的作用(剪切应变的突然降低),而对于有的部位产生了促震的作用(剪切应变的突然增加).
利用图 7a,c可以分析左断层内、外侧被监测单元的剪切应变的演变规律.由此可以发现,通常,这些被监测单元的剪切应变的演变都能表现出较好的同步性.例如,在虚线1及1″的位置,当左断层内侧的第23、25号被监测单元的剪切应变下降时,在左断层外侧的第55、57号被监测单元的剪切应变也下降,第25、55号被监测单元(编号相差30)的连线刚好垂直于左断层;在虚线2及2″的位置,第23、53号被监测单元的剪切应变同时表现为下降;在虚线4及4″的位置,第29、59号被监测单元的剪切应变同时表现为下降,等等.上述计算结果表明,通常,可以仅对断层一侧的被监测单元的剪切应变进行分析即可了解断层上事件的发生情况.上述结果与马胜利等(2008)的实验结果有所差异,他们发现,在雁列区贯通之前,断层内侧各点应变的释放引起外侧应变的台阶式上升,当雁列区贯通之后,断层内、外侧应变变化才趋于一致.
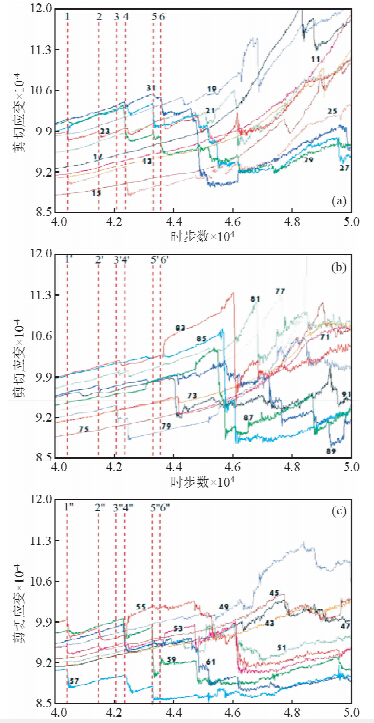 | 图 7 被监测单元剪切应变随着时步数的演变 (a)左断层内侧;(b)右断层内侧;(c)左断层外侧;虚线1、1′及1″对应相同的时步数,依此类推.Fig. 7 Evolution of shear strains of monitored elements with timestep numbers(a)At the inner sides of the left fault;(b)At the inner sides of the right fault;(c)At the outer sides of the left fault;the dotted lines1,1′ and 1″correspond to the same timestep number, and so on. |
我们重点关注那些较大的剪切应变降发生的地点及迁移规律.在图 8中,给出了超过5×10-6的剪切应变降在不同时段内的空间分布规律.如果将上述阈值取得过小,则可能标本各处都有剪切应变降;如果取得过高,可能捕捉不到剪切应变降.根据经验,上述阈值比较合适.每个时段持续1千个时步.第1个时段的结果为4万至4.1万个时步数之间的结果,依此类推.图 9给出了对剪切应变降的一些统计结果,分别是剪切应变降的的累计(在任一时段之内,将所有单元的剪切应变降量求和)、最大值及发生剪切应变降的单元数目.在图 8中,圆圈的半径定量代表剪切应变降的大小,剪切应变降的比例尺均相同,图 8各子图中的最大剪切应变降易于从图 9中看出.
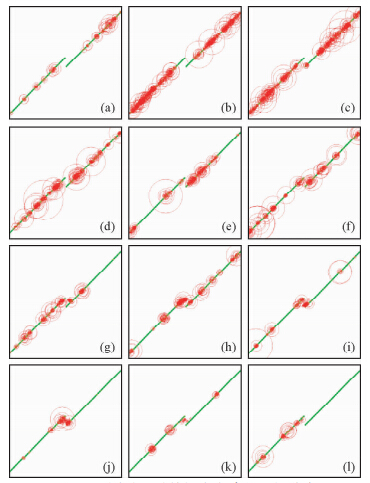 | 图 8 不同时段时剪切应变降的空间分布 (a)时段1;(b)时段4;(c)时段5;(d)时段7;(e)时段8;(f)时段9;(g)时段10;(h)时段11;(i)时段13;(j)时段14;(k)时段15;(l)时段16. Fig. 8 Distributions of shear strain decreases for different timestep intervals |
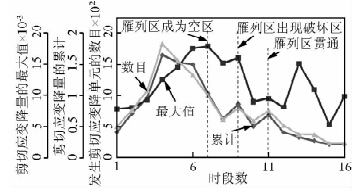 | 图 9 与剪切应变降有关的3种量的演变规律 Fig. 9 Evolution of three kinds of quantities related to shear strain decreases |
由图 8可以发现,随着σ1的值的增加,剪切应变降由远及近迁移.也就是说,由远离雁列区的断层附近,向雁列区附近迁移;之后,剪切应变降云集在雁列区附近;最终,仅两条断层附近个别位置发生剪切应变降.
在4.4万个时步数之前(第1~4个时段,图 8a~b),在雁列区附近,未观察到剪切应变降现象.这意味着雁列区及附近的断层尚未破坏.在远离雁列区的断层附近,剪切应变降密集分布,反映了在断层上发生了大量的破坏事件.剪切应变降的累计及发生剪切应变降(二者的演变规律一直类似)的单元数目在第4个时段内经历了最高值(图 9中左数第1条虚线).
当达到4.5万个时步数时(第5个时段,图 8c),左断层附近的剪切应变降已逼近雁列区,在右断层端部附近,已观察到剪切应变降.
当时步数在4.6~4.7万之间时(第7个时段,图 8d),尽管σ1的值持续增加,但在雁列区附近,未能观察到剪切应变降,雁列区形成了一个空区.此时,在左断层附近出现一个全局(第1~16个时段)最大的剪切应变降,其值约1.7×10-2(图 9).随后,当时步数在4.8~5.0万之间时(第9~10个时段,图 8f~g),上述空区消失.此时,雁列区内已出现破坏单元.
当时步数在5.0~5.1万之间时(第11个时段数,雁列区发生贯通,图 8h),剪切应变降云集在雁列区及附近的断层上,统计的与剪切应变降有关的3种量均不高(图 9中左数第3条虚线).
此后,剪切应变降累计及发生剪切应变降的单元数不断变少,在特定时段内,仅发生在两条断层的某些特定位置上,这些位置可能具有高的强度,因而有时剪切应变降的最大值并不小.
综合分析图 8可以发现,在4.1万个时步数之前,在特定时段之内,剪切应变降仅发生在某些特定位置上,它们彼此孤立.这应该是断层上少量的低强度单元破坏的反映.随后,随着σ1的值的增加,剪切应变降明显增加,发生剪切应变降的区域连成片,密集地分布在远离雁列区的断层附近.这应该是断层上大量的中等强度单元破坏的反映.当雁列区贯通之后,两条断层上某些位置仍可以观察到剪切应变降.这应该是断层上少量的高强度单元破坏的反映.
总之,随着σ1的值的增加,标本中的剪切应变降的表现先从平静变得活跃,雁列区曾一度成为空区,随后空区消失.当拉张雁列区贯通之后,剪切应变降的表现再一次回归平静.马胜利等(2008)通过实验发现,对于拉张雁列构造,雁列区破坏发生在前,而断层滑动发生在后;雁列区的破坏对断层滑动具有指示作用.在雁列区贯通之前的剪切应变降的活跃表现及雁列区之内空区的出现均具有一定的断层失稳前兆意义.由平静到活跃反映了标本应力或应变的增加而引起的发生在断层上的事件越来越多,空区的出现反映了标本应力或应变的增加过程中,拉张雁列区对断层错动一定程度的阻碍作用,尽管这种阻碍作用和挤压雁列的阻碍作用相比要小得多. 3 结 论
3.1 在拉张雁列区贯通过程中,观察到了启动于断层某一位置的破坏区,这根源于标本应力增加过程中两条断层的相互影响和作用.
3.2 在拉张雁列区贯通之前,观察到了一些被监测单元剪切应变的多次缓慢增加及之后的快速下降现象,这反映了标本应力增加过程中,断层上单元的不断破坏造成的卸载.
3.3 在拉张雁列区贯通之前,观察到了剪切应变降由远及近的迁移、雁列区成为空区及空区消失等现象,这些现象可视为断层失稳的前兆.
3.4 随着标本应力的增加,两条断层附近的剪切应变降依次表现为平静、活跃及平静.前后两个平静期与少量的低或高强度单元破坏有关,活跃期与大量的中等强度单元破坏有关.
3.5 在同一时刻,一条断层两侧相对位置的被监测单元的剪切应变演变规律比较类似,但不同断层附近的剪切应变演变规律非常复杂:有时突增,有时陡降,同步、非同步现象共存.这些复杂的表现根源于断层的非均质性及复杂的相互影响和作用,值得深入研究.
致 谢 衷心感谢本文第一作者的博士后合作导师马瑾院士的指导.| [1] | Aydin A, Schultz R A. 1990. Effect of mechanical interaction on the development of strike-slip faults with echelon patterns[J]. J. Struct. Geol.,12(1): 123-129. |
| [2] | Barker S L L. 2005.Pseudotachylyte-generating faults in Central Otago,New Zealand[J]. Tectonophysics,397(3-4): 211-223. |
| [3] | Beroza G C, Mikumo T. 1996. Short slip duration in dynamic rupture in the presence of heterogeneous fault properties[J]. J. Geophys. Res.,101 (B10): 22449-22460. |
| [4] | Bizzarri A, Cocco M, Andrews D J, et al. 2001. Solving the dynamic rupture problem with different numerical approaches and constitutive laws[J]. Geophys J Int.,144(3): 656-678. |
| [5] | Chen S Y, Liu L Q, Ma S L, et al. 2005.An experimental study on variation of b value during deformation of rock samples with different structural models[J]. Acta Seismologica Sinica (in Chinese), 27(3): 317-323. |
| [6] | de Joussineau G, Petit J P, Gauthier B D M. 2003. Photoelastic and numerical investigation of stress distributions around fault models under biaxial compressive loading conditions[J]. Tectonophysics,363(1-2): 19-43. |
| [7] | Du Y J, Aydin A. 1995.Shear fracture patterns and connectivity at geometric complexities along strike-slip faults[J]. J. Geophys. Res.,100(B9): 18093-18102. |
| [8] | Harris R A, Day S M. 1999. Dynamic 3D simulations of earthquakes on en echelon faults[J]. Geophys.Res. Lett.,26(14): 2089-2092. |
| [9] | Hillers G, Ben-Zion Y, Mai P M. 2006.Seismicity on a fault controlled by rate- and state-dependent friction with spatial variations of the critical slip distance[J]. J. Geophys. Res.,111(B1): B01403, doi: 10.1029/2005JB003859. |
| [10] | Jiang H K, Ma S L, Zhang L, et al. 2002. Spatio-temporal characteristics of acoustic emission during the deformation of rock samples with compressional and exten-sional en-echelon fault pattern[J]. Acta Seismologica Sinica (in Chinese), 24(4): 385-395. |
| [11] | Liu L Q, Ma J, Wu XQ. 1986. An experimental study on the process of deformation and instability for en-echelon faults[J]. Acta Seismologica Sinica (in Chinese), 8(4): 393-403. |
| [12] | Liu P X, Ma J, Liu L Q, et al. 2007. An experimental study on variation of thermal fields during the deformation of a compressive en echelon fault set[J]. Prog.Nat. Sci. (in Chinese), 17(4): 454-459. |
| [13] | Ma J, Du Y J, Liu L Q. 1986.The instability of en-echelon cracks and its precursors[J]. J. Phys. Earth.,34(Supplement): S141-S157. |
| [14] | Ma J, Liu L Q, Ma S L. 1999.Fault geometry and departure of precursors from epicenter[J]. Earthquake Research in China(in Chinese), 15(2): 106-115. |
| [15] | Ma J, Ma S L, Liu L Q, et al. 2002.Experimental study on patterns of fault interaction[J]. Progress in Natural Science(in Chinese), 12(5): 503-508. |
| [16] | Ma J, Liu L Q, Liu P X, et al. 2007.Thermal precursory pattern of fault unstable sliding: an experimental study of en echelon faults[J]. Chinese J. Geophys.(in Chinese), 50(4): 1141-1149. |
| [17] | Ma J, Ma S P, Liu P X, et al. 2008.Thermal field indicators for identifying active fault and its instability from laboratory experiments[J]. Seismology and Geology(in Chinese), 30(2): 363-382. |
| [18] | Ma J, Ma S P, Liu L Q, et al. 2010.Experimental study of thermal and strain fields during de-formation of en echelon faults and its geological implications[J]. Geodyn.Tectonophys.,1(1): 24-35. |
| [19] | Ma S L, Deng Z H, Ma W T, et al. 1995a. Experimental study on evolution of physical field during deformation of en-echelon faults(1)[J]. Seismology and Geology(in Chinese), 17(4): 327-335. |
| [20] | Ma S L, Liu L Q, Deng Z H, et al. 1995b. Experimental study on evolution of physical field during deformation of en-echelon faults(2)[J]. Seismology and Geology(in Chinese), 17(4): 336-341. |
| [21] | Ma S L, Jiang H K, Hu X Y, et al. 2004. A discussion on mechanism for seismic quiescence before large earthquakes based on experimental results of acoustic emission[J]. Seismology and Geology(in Chinese), 26(3): 426-435. |
| [22] | Ma S L, Chen S Y, Liu P X, et al. 2008. Effect of fault jogs on frictional behavior: An experimental study[J]. Scientia Sinica Terrae(in Chinese), 38(7): 842-851. |
| [23] | Ma W T, Ma J, Liu L Q, et al. 1995. The characteristics of acoustic emission in en echelon structure[J]. Seismology and Geology(in Chinese), 17(4): 342-348. |
| [24] | Miyatake T. 1992. Numerical simulation of three-dimensional faulting processes with heterogeneous rate- and state-dependent friction[J]. Tectonophysics,211(1-4): 223-232. |
| [25] | Ohlmacher G C, Berendsen P. 2005. Kinematics, mechanics, and potential earthquake hazards for faults in Pottawatomie County, Kansas, USA[J]. Tectonophysics,396(3-4): 227-244. |
| [26] | Olson J E, Pollard D D. 1991. The initiation and growth of enéchelonveins[J]. J. Struct. Geol.,13(5): 595-608. |
| [27] | Palusznya A, Matthib S K. 2009. Numerical modeling of discrete multi-crack growth applied to pattern formation in geological brittle media[J]. Int. J. Solids Struct.,46(18-19): 3383-3397. |
| [28] | Ren Y Q, Liu P X, Ma J, et al. 2013.Experimental study on evolution of thermal field of en echelon fault during the meta-instability stage[J]. Chinese J. Geophys.(in Chinese), 56(7): 2348-2357, doi: 10.6038/cjg20130721. |
| [29] | Segall P, Pollard D D. 1980. Mechanics of discontinuous faults[J]. J. Geophys. Res.,85(B8): 4337-4350. |
| [30] | Sibson R H. 1985. Stopping of earthquake ruptures at dilattionalfault jogs[J]. Nature, 316(6025): 248-251. |
| [31] | Smith J V, Yamauchi S. 2005.Kinematic interpretation of remnant en-echelon rift segments of the southwestern Japan Sea[J]. Tectonophysics,230(3-4): 143-150. |
| [32] | Soliva R, Maerten F, Petit J, et al. 2010. Field evidences for the role of static friction on fracture orientation in extensional relays along strike-slip faults: Comparison with photoelasticity and 3-D numerical modeling[J]. J. Struct. Geol.,32(11): 1721-1731. |
| [33] | Swanson M T. 1990.Extensional duplexing in the York Cliffs strike-slip fault system, southern coastal Maine[J]. J. Struct. Geol.,12(4): 499-512. |
| [34] | Talwani P. 1999.Fault geometry and earthquakes in continental interiors[J]. Tectonophysics,305(1-3): 371-379. |
| [35] | Thomas A L, Pollard D D. 1993. The geometry of echelon fractures in rock: implications from laboratory and numerical experiments[J]. J. Struct. Geol.,15(3-5): 323-334. |
| [36] | Wang X B, Ma J, Liu L Q. 2010. Numerical simulation of failed zone propagation process and anomalies related to the released energy during a compressive jog intersection[J]. J. Mech. Mat. Struct.,5(6): 1007-1022. |
| [37] | Wang X B,Ma J, Liu L Q. 2012. A comparison of mechanical behavior and frequency-energy relations for two kinds of echelon fault structures through numerical simulation[J]. Pure Appl. Geophys.,169(11): 1927-1945. |
| [38] | Wang X B, Ma J, Pan Y S. 2013a. Numerical simulation of stick-slip behaviours of typical faults in biaxial compression based on a frictional-hardening and frictional-softening model[J]. Geophys.J. Int.,194(2): 1023-1041. |
| [39] | Wang X B, Ma J, Liu L Q. 2013b. Numerical simulation of large shear strain drops during jog failure for echelon faults based on a heterogeneous and strain-softening model[J]. Tectonophysics, 608: 667-684. |
| [40] | Wang X B, Gu L, Ma B, et al. 2013c. A Frequency-energy method to determine the hazard faults among faults and numerical simulation[J]. Progress in Geophysics(in Chinese), 28(5): 2739-2747, doi: 10.6038/pg20130558. |
| [41] | Wang X B, Lü J Q, Ma B, et al. 2014. Effects of fault spacing on the deformation, failure process and released energy for the extensional echelon faults: a numerical simulation[J]. Progress in Geophysics(in Chinese), 29(1): 406-411, doi: 10.6038/pg20140158. |
| [42] | Zachariasen J, Sieh K. 1995. The transfer of slip between two en echelon strike-slip faults: a case study from the 1992 Landers earthquake, southern California[J]. J. Geophys. Res.,100(B8): 15281-15301. |
| [43] | 陈顺云, 刘力强, 马胜利,等. 2005. 构造活动模式变化对b值影响的实验研究[J]. 地震学报, 27(3): 317-323. |
| [44] | 蒋海昆, 马胜利, 张流,等. 2002. 雁列式断层组合变形过程中的声发射活动特征[J]. 地震学报, 24(4): 385-395. |
| [45] | 刘力强, 马瑾, 吴秀泉. 1986. 雁列式断层变形与失稳过程的实验研究[J]. 地震学报, 8(4): 393-403. |
| [46] | 刘培洵, 马瑾, 刘力强,等. 2007. 压性雁列构造变形过程中热场演化的实验研究[J]. 自然科学进展, 17(4): 454-459. |
| [47] | 马瑾, 刘力强, 马胜利. 1999. 断层几何与前兆偏离[J]. 中国地震, 15(2): 106-115. |
| [48] | 马瑾, 马胜利, 刘力强,等. 2002. 断层相互作用型式的实验研究[J]. 自然科学进展, 12(5): 503-508. |
| [49] | 马瑾, 刘力强, 刘培洵,等. 2007. 断层失稳错动热场前兆模式: 雁列断层的实验研究[J]. 地球物理学报, 50(4): 1141-1149. |
| [50] | 马瑾, 马少鹏, 刘培洵,等. 2008. 识别断层活动和失稳的热场标志—实验室的证据[J]. 地震地质, 30(2): 363-382. |
| [51] | 马胜利, 邓志辉, 马文涛,等. 1995a. 雁列式断层变形过程中物理场演化的实验研究(一)[J]. 地震地质, 17(4): 327-335. |
| [52] | 马胜利, 刘力强, 邓志辉,等. 1995b. 雁列式断层变形过程中物理场演化的实验研究(二)[J]. 地震地质, 17(4): 336-341. |
| [53] | 马胜利, 蒋海昆, 扈小燕,等. 2004. 基于声发射实验结果讨论大震前地震活动平静现象的机制[J]. 地震地质, 26(3): 426-435. |
| [54] | 马胜利, 陈顺云, 刘培洵,等. 2008. 断层阶区对滑动行为影响的实验研究[J]. 中国科学D辑: 地球科学, 38(7): 842-851. |
| [55] | 马文涛, 马瑾, 刘力强,等. 1995. 雁列断层变形过程中的声发射特征[J]. 地震地质, 17(4): 342-348. |
| [56] | 任雅琼, 刘培洵, 马瑾,等. 2013. 亚失稳阶段雁列断层热场演化的实验研究[J]. 地球物理学报, 56(7): 2348-2357, doi: 10.6038/cjg20130721. |
| [57] | 王学滨, 顾路, 马冰,等. 2013. 断层系统中危险断层识别的频次-能量方法及数值模拟[J]. 地球物理学进展, 28(5): 2739-2747, doi: 10.6038/pg20130558. |
| [58] | 王学滨, 吕家庆, 马冰,等. 2014. 断层间距对拉张雁列构造破坏过程及能量释放影响的模拟[J]. 地球物理学进展, 29(1): 406-411, doi: 10.6038/pg20140158. |
 2014, Vol. 29
2014, Vol. 29

