2. 中国地质大学(北京), 北京 100083;
3. 安徽省地质环境监测总站, 合肥 230001
2. China University of Geosciences, Beijing 100083, China;
3. Anhui Institute Of Geo-Environment Monitoring, Hefei 230001, China
大面积的强夯地基处理效果检测除了要求测试加固后地基土体的承载力和变形参数外,还应该关注地基处理效果的横向均匀性和加固深度.因此,仅靠载荷试验等常规检测方法无法胜任强夯地基处理效果的检测.随着强夯在地基处理中的大量使用,传统方法已显得不足,亟需寻求更有效的检测办法.
自20世纪50年代初人们发现瑞雷波的频散特征后,就开始了利用天然地震记录中的瑞雷波探测地球内部结构的研究(Haskell,1953),并开始利用瑞雷波测试土的弹性模量(Addo and Robertson, 1959),70年代人们开始利用人工激发的瑞雷波解决浅层工程地质问题(Chang and Ballard, 1973;潘佳铁等,2011;余大新等,2014).1984 年Nazarian对瑞雷波在地质工程探测中的应用做了总结并对瑞雷波现场测试方法进行简化,反演出了土层的模量(Nazarian,1984).至此,瑞雷波探测开始应用到工程检测中.近20年来人们对瑞雷波相速度与地基承载力、变形模量之间的关系也做了大量的研究工作,得出各种非线性的数学关系式(杨成林,1993;陈宏林和丰继林,1998;潘冬明等,2010).利用瑞雷波频散曲线求取岩土介质的力学参数是反演的核心问题,也是瑞雷波勘探的关键环节(李杰等,2013).虽然国内外学者在这方面研究很多(白朝旭等,2007),但这一问题一直没有得到很好的解决.
利用瑞雷波频散性及瑞雷波相速度与岩土介质特性的密切相关性检测强夯处理地基具有很多优越性:分辨率高、受场地影响小、设备简单、快捷等,且能够胜任大面积地基处理效果的跟踪检测(陈祥和孙进忠,2006).本文将多道瞬态瑞雷瑞雷波技术应用于北京艾尔标准厂房及配套楼地基强夯处理效果检测,采用瑞雷波测试与载荷试验和取土试验相 结合的方法,统计出瑞雷波相速度与场地岩土体物理力学参数之间的关系式,完成了该场地强夯地基处理效果的检测评价.
1 瑞雷波法的检测原理
瑞雷波是沿介质表面或层面传播的一种弹性波动,波动能量集中在界面附近一定的范围内,离开界面一定距离后其能量迅速衰减,在界面附近其质点振动方式为长轴位于界面法线方向上的逆进椭圆.瑞雷波在非均匀介质中的相速度VR随频率f变化而变化(即瑞雷波的频散性);瑞雷波相速度VR与岩土介质性质密切相关.这为利用瑞雷波检测强夯处理地基提供了理论基础.利用瑞雷波的频散特征求得岩土体中相速度VR的分布,相速度VR可以定性评价强夯地基处理效果.然后再利用相速度与岩土体物理力学参数的相关性反演出场地大范围的物理力学参数,由此对地基岩土体做出定量评价(Sun et al.,2002,2004,2007;田爱萍等,2009;陈昌彦等,2010).
依震源不同瑞雷波测试方法分稳态法和瞬态法两种.稳态法靠不断改变激震装置的输出功率,即可得到不同频率所对应的瑞雷波相速度.该法提取瑞雷波相速度简单明了,但是现场测试比较费时.瞬态法只需重锤锤击地面一次,在激发点产生垂向脉冲,从而在介质中激发出具有一定频率带宽的混频瑞雷波动.利用频谱分析技术提取各个单频成分的瑞雷波相速度,即可得到瑞雷波的频散曲线.与稳态法相比较,瞬态法提取瑞雷波相速度的分析方法比较复杂,但是现场测试只需重锤一击即可完成,激震装置简单,现场测试工作量远远小于稳态法,适用性更好.
关于提取瑞雷波频散曲线,首先要分析两个测点间不同频率成分波动的相位差Δφ,将两个测点间波动的相位差Δφ分解为两个部分:
一是相对于两个测点上瑞雷波初至的初相位之差Δψ(0≤Δψ≤2π);
二是两个测点上瑞雷波到时差τ导致的相位延迟2πfτ,即:Δφ=Δψ+ 2πfτ,这是保证在所有频段上,特别是高频段上,提取得到稳定可靠的频散曲线的关键(祁生文等,2001;Chen et al., 2006;刘雪明等,2009).
用锤击使地面产生一个包含所需频率范围的混频瑞雷波动,假设离震源一定距离处有一观测点M,记录到的瑞雷波是f1(t),根据傅里叶变换,其频谱为
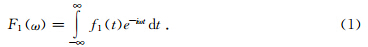
在波的前进方向上与M点相距为Δx的观测点N同样也记录到时间信号f2(t),其频谱是:
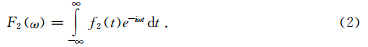
若波从M点传播到N点,它们之间的变化完全是频散引起的,则应有下列的关系式:



根据上式,只要知道M、N两点间的距离Δx和每一频率的相位差,就可以求出每一频率的相速度VR.
根据瑞雷波测试记录提取瑞雷波相速度VR,利用波长、相速度和频率的关系λ=VR / f以及影响深度H与其波长的关系H=β·λ转换求取相速度深度曲线VR-H,进而获得整条测线上(多道测试)不同深度上的瑞雷波相速度分布剖面.联合所有测线的结果,即可获得整个地基范围内的瑞雷波相速度的空间分布VR.
但是瑞雷波相速度VR不能作为基础设计的依据,只能定性评价地基夯实效果.为解决这一问题,需要通过一定数量的原位测试和土工试验得出地基承载力fka、变形模量E0、压实系数k等物理力学参数,进而基于瑞雷波相速度与岩土体介质之间的密切相关性,拟合出VR与fka、E0、k之间的相关关系,利用场地地基瑞雷波相速度VR的分布和上述相关关系,即可换算得到场地的fka、E0、k分布.根据fka、E0、k的分布情况,就能有效、全面地定量评估强夯处理地基夯实效果,为基础设计、施工及后期的沉降预测提供依据.
2 工程实例及分析
2.1 工程概况
北京艾尔标准厂房及配套楼项目位于北京市房山区良乡镇富庄村东北侧良乡工业开发区内,西临京广铁路,距离约200 m,场地周边有几家机械加工厂.建筑物为钢结构厂房及附属用房1栋,地上1层,高度不大于12.0 m,钢结构,无地下室;专家公寓楼1栋,地上3层,地下1层,框架结构,独立基础;警卫室1栋,地上1层,地下1层,砖混结构,条形基础,建筑地基面积为180×88 m2.设计要求地基承载力标准值fka≥200 kPa,压实系数不小于9.5.
检测采用瑞雷波法与静载试验和现场取土试验(测压实系数)相结合的联合检测方法.瑞雷波采集采用多道瞬态法;使用仪器为SWG工程地震仪和SSJ-4.5型低频检波器;现场共布置13条测线,如图 1,每条测线按道间距9 m布设12支检波器.现场布置20个试验点,每个试验点进行一组静载试验并取三个测试土样,共20个载荷试验和60组压实系数测试土样.
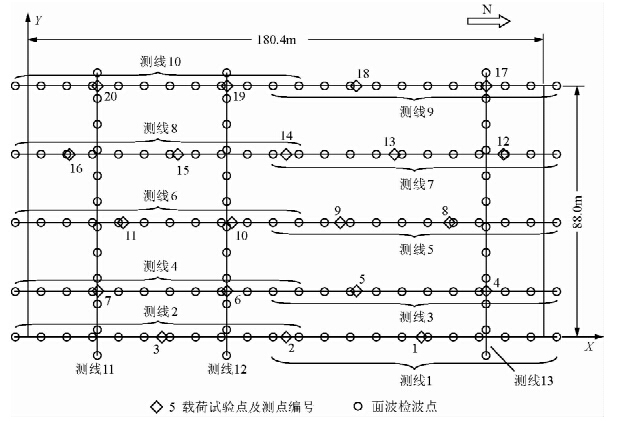 | 图 1 场地面波测线及荷载试验点布置图Fig. 1 Sketch of Rayleigh wave measure lines and loading test pints on the site |
在进行瑞雷波检测前,首先根据工程需要的检测深度确定瑞雷波的工作频率范围,进而选定震源激发装置.
设瑞雷波在地表的振幅为U0,在深度z处振幅衰减为Uz,一般认为当

| | 表 1 不同介质中瑞雷波的穿透深度 Table 1 Penetration depth of Rayleigh wave in different medium |
对各种介质,瑞雷波的穿透深度在0.550λR ~0.875λR之间.对于土体,泊松比ν=0.40~0.45,穿透深度约为0.79λR ~0.84λR.本工程场地填夯的工程岩土体为粉质黏土,取泊松比ν=0.40,H=0.79λR.
本工程地基回填土最深约6 m,强夯处理的有效影响深度要求大10 m,因此可把检测深度定为15 m.当检测深度H=15 m时,则要求所激发的瑞雷波中所含最长波成分应达到λR=19 m.场地15 m深度以上的工程岩土体的平均相速度按VR=250 m/s考虑,根据公式:

介质浅部的检测靠瑞雷波中的高频部分.鉴于此次检测的目的是强夯处理效果的检测,加之土体表层有冻结,因此过于追求浅部工程岩土体的分辨没意义,将分辨上限定为1 m是即可满足要求.按H=1m计,仍取相速度V R=250 m/s,可得出本次检测的工作频段最高频率应在197 Hz左右.
综上所述,本次瑞雷波检测的工作频段应为13~197 Hz.
根据以往检测经验,采用18磅重锤锤击地面即可产生满足工作频段的瑞雷波.源检距为10 m左右,使检波器拾取到的波形便于识别.为提高信噪比,在激发点放置一块直径约为20 cm的圆形钢板.每个激发点进行数次激发,至少保存两个波形良好的瑞雷波记录文件,以保证取得良好的记录数据.
2.3 检测结果
首先对每一次激发所取得记录波形进行震相分析,认清各道记录波形中瑞雷瑞雷波震相的出现时段;然后,通过对相邻两道波形进行相关和频域分析,提取每两道波形之间各个频率成分对应的相速度VR,生成相速度—深度曲线(VR-H),如图 2,该曲线反映了瑞雷波相速度沿深度的变化.联合测线上所有的相速度-深度曲线,得出该测线的相速度-深度剖面图,如图 3,该剖面清晰地反映了测线下每一点的瑞雷波相速度.
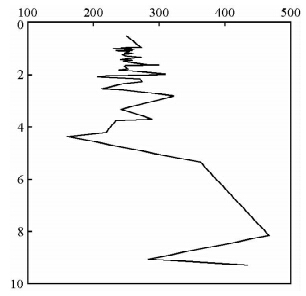 | 图 2 4号测线5-6检波器间VR-H曲线Fig. 2 The VR-H plot of 5-6 detectors of NO.4 |
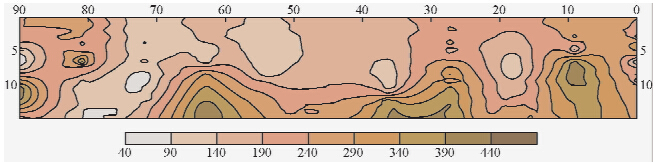 | 图 3 11号测线面波速度VR-H剖面图Fig. 3 VR-H section of measure line 11 |
13条瑞雷波测线控制了整个场地的瑞雷波相速度的空间分布情况,根据各测点相速度-深度曲线统计场地0.5 m和4.0 m深度处的瑞雷波相速度,可得到场地岩土体在0.5 m和4.0 m深度处的瑞雷波相速度平面分布,如图 4、图 5所示.
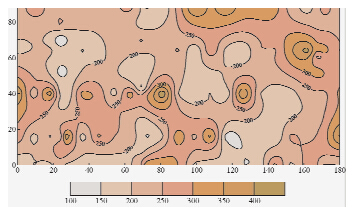 | 图 4 场地0.5 m深度瑞雷波速度平面分布图Fig. 4 VR contour of the site on the depth 0.5 m |
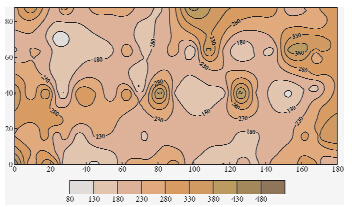 | 图 5 场地4.0 m深度瑞雷波速度平面分布图Fig. 5 VR contour of the site on the depth 4.0 m |
从图 4可知:0.5 m深度处瑞雷波相速度变化范围主要在220~300 m/s之间,局部相速度低于200 m/s,存在3个相对低速区(图中白色区域).从图 5可知:4.0 m深度处瑞雷波相速度变化范围主要在260~320 m/s之间,局部相速度低于200 m/s.从整体上看,强夯处理比较均匀,至于压实程度、承载力、变形能否达到要求,下面将VR和压实系数k、地基承载力fka、变形模量E0做相关性分析即知.
静载试验得出地基承载力为250~320 kPa,变形模量为30~40 MPa,均能满足设计要求;压实系数在0.93~0.96左右,个别点压实系数小于0.95,基本上满足设计要求.但是原位测试数据仅能说明试验点强夯处理效果,为了全面掌握强夯处理效果,将VR和压实系数k、地基承载力fka、变形模量E0做相关性分析.然后反演出整个场地的压实系数k、地基承载力fka、变形模量E0.
某深度处的瑞雷波相速度受该深度以上各层岩土体的影响,即瑞雷波相速度可以反映对应深度范围内岩土体的总体特性.选择多大深度处的瑞雷波相速度与静载试验得出的地基承载力fka和变形模量E0以及压实系数k做相关分析是利用瑞雷波定量评价地基处理效果必须解决的问题.原则上所选择的深度应该与静载试验影响深度相当.静载试验的附加应力对地基的影响深度按照地基变形计算深度确定,一般取附加应力与自重应力的比值为0.2的深度处作为沉降计算深度的界限(陈仲颐,1994;陈祥等,2004).据此计算得该工程静载试验的附加应力影响深度为3.7 m.同时,有关文献通过分析对比,认为用4.0 m深度对应的瑞雷波相速度评价地基处理效果较为合适(祁生文,1999).综合分析后,取4.0 m深度处的瑞雷波相速度与静载试验得出的地基承载力fka和变形模量E0做相关分析.由于压实系数的测试土样取自0.5 m深度处,故取0.5 m深度处的瑞雷波相速度与压实系数做相关分析.
(1)瑞雷波相速度VR与压实系数k相关分析
图 6为压实系数k与瑞雷波相速度散点图.从散点图可知瑞雷波相速度与压实系数之间存在明显的线性相关性,相关系数r=0.80,VR-k关系式为

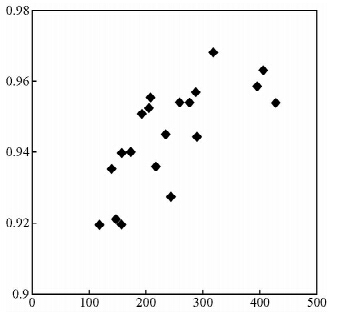 | 图 6 瑞雷波相速度VR与压实系数k散点图Fig. 6 Relationship between VR and k |
从图 7可以得到场地强夯处理地基压实系数在0.93~0.96之间,存在3个低值区(图中浅色区域),最低值大于0.93,基本达到压实系数0.95的要求.压实系数k等值线图的低值区和0.5 m深度瑞雷波相速度的低值区是一致的.
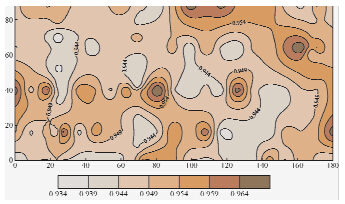 | 图 7 场地压实系数k平面分布图Fig. 7 k contour of the site in the rayleigh layer of soil on the depth 0.5 m |
(2)瑞雷波相速度VR与承载力fka相关分析
图 8为承载力与瑞雷波相速度散点图,从散点图可知瑞雷波相速度与承载力之间的线性相关性明显,相关性系数为0.87,VR-fka关系式为

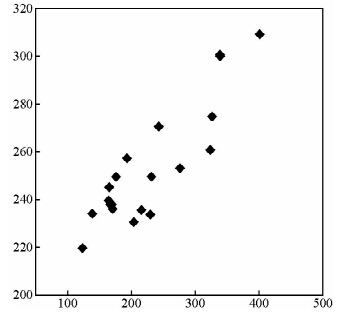 | 图 8 瑞雷波相速度VR与承载力fka散点图Fig. 8 Relationship between VR and fka |
基于大范围的瑞雷波相速度VR,通过VR-fka关系式反演出整个场地的地基承载力,生成场地地基承载力平面分布等值线图,如图 8所示.
从图 9可以得出,地基承载力主要在250~320 kPa,整个场地地基承载力均大于200 kPa,满足设计要求的承载力fka≥200 kPa.地基承载力fka等值线图也存在相应的低值区和相应高值区.
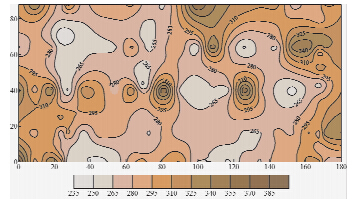 | 图 9 场地承载力fka平面分布图Fig. 9 fka contour of the site |
(3)瑞雷波相速度VR与变形模量E0相关分析
图 10为承载力与瑞雷波相速度散点图,从散点图可知瑞雷波相速度和变形模量之间线性相关性明显,相关性系数为0.86,VR-E0关系式为

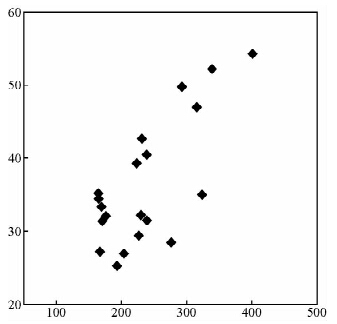 | 图 10 瑞雷波相速度VR与变形模量E0散点图Fig. 10 Relationship between VR and E0 |
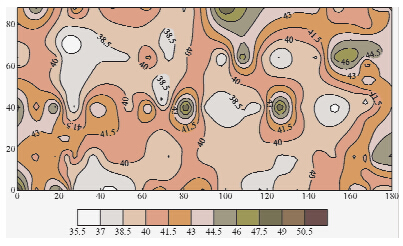 | 图 11 场地变形模量E0平面分布图Fig. 11 E0 contour of the site |
地基岩土体变形模量主要在35~40 MPa之间,最小为25 MPa,最大达65 MPa.这种极值只出现在局部区域,即图中白色区域.根据地基承载力和变形模量计算地基沉降量,最大沉降量为8.0 mm,最小沉降量为5.8 mm.按照最不利原则,取距离场地变形模量最大区域中心点M最近处的最小变形模量区域中心点N,如图 11中M、N所示,量取线段MN长度,换算成实际距离,约为36.9 m,则基础的局部倾斜约为:(8.0~5.8)mm/36.9 m=0.000059<0.002,满足规范要求(GB 5007—2002,2002).总之,本工程地基强夯处理较均匀,满足要求. 3 检测结论
检测结果表明,北京艾尔标准厂房及配套楼地基经强夯加固之后,承载力在250~320 kPa之间,变形模量在35~40 MPa之间,完全达到设计要求;压实系数在0.93~0.96之间,基本达到设计要求,个别不足之处需做进一步处理. 4 小结和认识
4.1 瑞雷波相速度与夯实地基岩土体物理力学参数之间相关性明显,通过它们之间的函数关系式反演出整个场地的物理力学参数,得出的等值线图能全面反映整个场地的夯实效果,克服了传统方法只能对有限测点进行抽检的缺点.
4.2 由于瑞雷波测试结果是测线下岩土体的综合性质,当岩土体性质竖向变化较大时,瑞雷波相速度与压实系数之间的离散性会很大,导致无法拟合,也就不能做反演.反之则可以做相关分析.
4.3 本工程场地瑞雷波相速度与岩土体承载力、变形模量之间存在明显的线性相关性,而很多文献得出非线性关系.地基承载力和变形模量等物理力学参数是一定深度范围内岩土体特性的综合反映,瑞雷波相速度同样也是对应深度范围内岩土体特性的综合反映,为了进一步揭示它们之间的相关性,需要更多的试验研究.
致 谢 感谢审稿专家和编辑部的大力支持.| [1] | Addo K O, Robertson P K. 1959. Shear-wave velocity measurement of soils using Rayleigh waves[J]. Canadian Geotechnical Journal, 29(4): 558-568. |
| [2] | Bai C X, Liu Y, Wang D, et al. 2007. The application of Rayleigh wave testing techniques in geotechnical engineering[J]. Progress in Geophysics, (in Chinese), 22(6): 1959-1965, doi: 10.3969/j.issn.1004-2903.2007.06.046. |
| [3] | Chang F K, Ballard R F. 1973. Rayleigh-wave dispersion technique for rapid subsurface exploration[C].// The 43 rd international geophysical academic conference. |
| [4] | Chen C Y, Bai C X, Song L L, et al. 2010. Application of the multi-channel transient Rayleigh wave method to highway goaf detection[J]. Progress in Geophysics, (in Chinese), 25(2): 701-708, doi: 10.3969/j.issn.1004-2903.2010.02.045. |
| [5] | Chen H L, Feng J L. 1998. Engineering Earthquake Prospect Method (in Chinese)[M].Beijing: Earthquake Press. |
| [6] | Chen X, Sun J Z, Liu J R. 2004. Mechanism of zigzag dispersion curve of Rayleigh waves[J]. Progress in Geophysics (in Chinese), 19(4): 860-863, doi: 10.3969/j.issn.1004-2903.2004.04.025. |
| [7] | Chen X, Sun J Z. 2006. An improved equivalent homogenous half-space method and reverse fitting analysis of Rayleigh wave dispersion curve[J]. Chinese Journal of Geophysics, 49(2): 569-576. |
| [8] | Chen Z Y. 1994. Soil Mechanics (in Chinese)[M]. Beijing: Tsinghua University Press. |
| [9] | GB5007-2002. 2002. Code for design of building foundation [S]. |
| [10] | Haskell N A. 1953. The dispersion of surface waves on multilayered media[J]. Bulletin of the Seismological Society of America, 43(1): 17-34. |
| [11] | Li J, Yang J, Chen X, Chen X H. 2013. Software design of genetic algorithm for rayleigh wave dispersion curve inversion[J]. Progress in Geophysics (in Chinese), 28(5): 2693-2700, doi: 10.6038/pg20130552. |
| [12] | Liu X M, Fan Y H, Zhai J Y, et al. 2009. Numerical simulation of Rayleigh wave zigzag dispersion curves of four typical strata[J]. Chinese Journal of Geophysics (in Chinese), 52(12): 3042-3050, doi: 10.3969/j.issn.0001-5733.2009.12.013. |
| [13] | Nazarian S. 1984. In-situ determination of elastic moduli of soil deposits and pavement systems by spectral-analysis-of-surface waves method[Ph. D. thesis]. Texas: University of Texas, Austin. |
| [14] | Pan D M, Hu M S, Cui R F, et al. 2010. Dispersion analysis of Rayleigh surface waves and application based on Radon transform[J]. Chinese Journal of Geophysics (in Chinese), 53(11): 2760-2766, doi: 10.3969/j.issn.0001-5733.2010.11.025. |
| [15] | Pan J T, Wu Q J, Li Y H, et al. 2011. Rayleigh wave tomography of the phase velocity in North China[J]. Chinese Journal of Geophysics (in Chinese), 54(1): 67-76, doi: 10.3969/j.issn.0001-5733.2011.01.008. |
| [16] | Qi S W. 1999. The theory of Rayleigh wave exploration and its application in the test of dynamic consolidation effect of Houshi power plant foundation [D]. Beijing: China University of Geosciences (Beijing). |
| [17] | Qi S W, Sun J Z, Wan Z Q. 2001. Some improvements in transient Rayleigh wave exploration method[J]. Journal of Liaoning Technical University (Natural Science Edition) (in Chinese), 20(4): 466-468. |
| [18] | Sun J Z, Zhang H, Feng Y G. 2002. Application of surface wave detection to the assessment of the weathering situation of stone relics[C].// The proceedings of the 2nd international conference-new development in rock mechanics and rock engineering. Princeton: Rinton Press, 542-545. |
| [19] | Sun J Z, Qi S W, Zhang H. 2004. Application of Rayleigh wave detection in nondestructive testing for engineering[J]. Journal of Engineering Geology, 12(S1): 427-432. |
| [20] | Sun J Z, Chen X, Tian X F. 2007. Engineering infrastructure nondestructive testing with Rayleigh waves: case studies in transportation and archaeology[J]. Journal of Geophysics and Engineering, 4(3): 268-275. |
| [21] | Tian A P, Liu Y Q, Dai Y J, et al. 2009. Rayleigh wave detection dynamic consolidation effect of foundation at the Nankou sewage treatment plant[J]. Progress in Geophysics (in Chinese), 24(4): 1533-1539, doi: 10.3969/j.issn.1004-2903.2009.04.049. |
| [22] | Yang C L. 1993. Rayleigh Wave Exploration (in Chinese)[M]. Beijing: Geological Press. |
| [23] | Yu D X, Li Y H, Wu Q J, et al. 2014. S-wave velocity structure of the northeastern Tibetan Plateau from joint inversion of Rayleigh wave phase and group velocities[J]. Chinese Journal of Geophysics (in Chinese), 57(3): 800-811, doi: 10.6038/cjg20140310. |
| [24] | 白朝旭, 刘洋, 王典,等. 2007. 瑞雷波测试技术在岩土工程中的应用研究[J]. 地球物理学进展, 22(6): 1959-1965, doi: 10.3969/j.issn.1004-2903.2007.06.046. |
| [25] | 陈昌彦, 白朝旭, 宋连亮,等. 2010. 多道瞬态瑞雷波技术在公路采空塌陷区探测中应用[J]. 地球物理学进展, 25(2): 701-708, doi: 10.3969/j.issn.1004-2903.2010.02.045. |
| [26] | 陈宏林, 丰继林. 1998. 工程地震勘察方法[M]. 北京: 地震出版社. |
| [27] | 陈祥, 孙进忠, 刘景儒. 2004. 瑞雷波“之”形速度—深度曲线的成因[J]. 地球物理学进展, 19(4): 860-863, doi: 10.3969/j.issn.1004-2903.2004.04.025. |
| [28] | 陈祥, 孙进忠. 2006. 改进的等效半空间法及瑞雷波频散曲线反演[J]. 地球物理学报, 49(2): 569-576. |
| [29] | 陈仲颐. 1994. 土力学[M]. 北京: 清华大学出版社. |
| [30] | GB 5007-2002. 2002.建筑地基基础设计规范[S]. |
| [31] | 李杰, 杨婧, 陈宣华. 2013. 面波频散曲线遗传算法反演的程序设计[J]. 地球物理学进展, 28(5): 2693-2700, doi: 10.6038/pg20130552. |
| [32] | 刘雪明, 凡友华, 翟佳羽,等. 2009. 四种典型地层的瑞雷波“之”字型频散曲线数值模拟研究[J]. 地球物理学报, 52(12): 3042-3050, doi: 10.3969/j.issn.0001-5733.2009.12.013. |
| [33] | 潘冬明, 胡明顺, 崔若飞,等. 2010. 基于拉东变换的瑞雷面波频散分析与应用[J]. 地球物理学报, 53(11): 2760-2766, doi: 10.3969/j.issn.0001-5733.2010.11.025. |
| [34] | 潘佳铁, 吴庆举, 李永华,等. 2011. 华北地区瑞雷面波相速度层析成像[J]. 地球物理学报, 54(1): 67-76, doi: 10.3969/j.issn.0001-5733.2011.01.008. |
| [35] | 祁生文. 1999. 瑞雷波勘探原理及其在漳州后石电厂地基强夯效果检测中的应用[硕士论文]. 北京: 中国地质大学(北京). |
| [36] | 祁生文, 孙进忠, 万志清. 2001. 瞬态瑞雷波勘探方法的一点改进[J]. 辽宁工程技术大学学报, 20(4): 466-468. |
| [37] | 田爱萍, 柳亚千, 戴彦杰,等. 2009. 南口污水处理厂强夯处理地基瑞雷波检测[J]. 地球物理学进展, 24(4): 1533-1539, doi: 10.3969/j.issn.1004-2903.2009.04.049. |
| [38] | 杨成林. 1993. 瑞雷波勘探[M]. 北京: 地质出版社. |
| [39] | 余大新, 李永华, 吴庆举,等. 2014. 利用Rayleigh波相速度和群速度联合反演青藏高原东北缘S波速度结构[J]. 地球物理学报, 57(3): 800-811, doi: 10.6038/cjg20140310. |
 2014, Vol. 29
2014, Vol. 29

