2. 山东省东营职业学院, 东营 257091;
3. 中石化胜利油田有限公司物探研究院, 东营 257022
2. Vocation College, Dong Ying city, Dongying 257091, China;
3. Geophysical Research Institute of Shengli Oilfield Company Limited SINOPEC, Dongying 257002, China
基于VSP的传统时深标定技术在相对简单的构造圈闭的勘探开发方面取得了良好的效果(王保利和朱光明,2009;姜本厚等,2012;刘守伟等,2012),对于多数构造圈闭,VSP时深关系应用于偏移剖面时所存在误差,都被井点校正挽救了回来(刘海河,2004;郝守玲和赵群,2008),因为构造形态通常由地震剖面上一组近似平行的同相轴来反映(王成礼等,1996;孟恩等,2005; 张兵等,2008;张广智等,2011),高低几个同相轴不会改变构造的形态.但是进入地震储层预测和描述领域,必须把储层顶底界面与其对应的地震反射准确对应起来,才能给出储层的正确描述,此时井点校正对于解决储层与剖面的正确对应关系已经无能为力(王玉贵等,2008;郭念民和吴国忱,2012).
但传统基于VSP时深标定技术不能适应储层预测和描述的需要,该技术不仅存在基本的理论缺陷(传统时深标定缺乏对VSP时深关系的深入研究,忽略了VSP“时间”与偏移剖面“时间”的不同),技术上也过于粗糙和单一(只适应相对简单的构造圈闭或席状储层的描述,对于复杂储层如河流相储层的描述基本不适应(陈启林和杨占龙,2006;黄中玉等,2008;陈生昌等,2012).而且判别手段过于单一,基本只有合成地震记录一种方法,陷阱较多),不能满足储层预测、复杂构造、低幅度构造等诸多勘探开发工作的需要(李庆忠和张进,2006;张振国等,2010).
时深关系的精确与否直接关系地震资料解释的准确度,在地震资料解释过程中处于上游阶段(李庆忠和张进,2006;He,2006;He et al., 2007; 李伍志等,2011),时深关系不准确会导致整个解释过程重新开展,因此获取精确地时深关系尤为重要.在各种时深关系获取中VSP资料最为准确(王保利等,2009;张振国等,2010;高磊等,2013),然而传统的VSP时深标定都是基于地层倾角为零的基本假设,在地层为平层或地层倾角很小的情况下对于地震资料的解释而言是准确的(方伍宝和陈林,2006;杜婧等,2009;吴世萍等,2011).但是当地层倾角较大时,与平层相比VSP走时存在很大的误差,若依然按照平层模型进行时深标定则会发生层位串层现象,导致地震资料解释不准确.
倾斜地层的存在导致时深关系不准确,关于时深关系很难用统一的解析表达式表示,特别是对于多层介质的情况(Hornby and Yu, 2007;孙文博和孙赞东,2010).本文采用基于高阶有限差分数值模拟的方法实现VSP正演模拟,利用初至拾取得到时深关系.通过倾斜地层和平层地层的对比分析时深关系时差来源,定量分析VSP走时误差,通过时深关系校正实现VSP记录与地面地震精确标定.并通过系统设计和软件研发,建立了一套VSP时差分析校正软件,为储层预测及地震解释提供了新的技术平台.
1 初至拾取
地震波传播时满足Snell定律(即时间最小原理)如图 1所示.以单斜介质为例,位于斜层之上的时候,射线路径一样,位于斜层之下的时候,不同的深度点对应的深度不同.从图上可以得到地层倾斜时波的路径与地层交点已经偏离井与地层交点.下行波的初值时间走时已经不能正确反映过井点处的时间深度.由于不同点处的射线路径不一样,所以用射线追踪的方法拾取初至时间变得非常麻烦,本文采用波动方程来拾取初至时间.
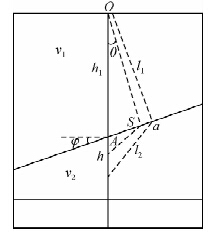 | 图 1 射线路径示意图 Fig. 1 Schematic diagram of the ray path |
下面推导单斜介质时理论误差的求取.如图 1所示,推导过程如下:
当深度小于第一层深度时,有
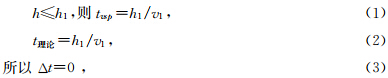
当深度大于第一层深度时,
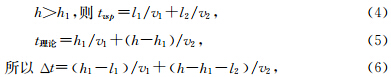
l2=sqrt s2+(h-h1)2+2s(h-h1)cosφ
s=h1sinθ/cos φ-θ .
为了求出射线路径,我们还以单斜模型为例:为了求出上面θ角度大小,根据shell定律,波的射线路径是时间最小的路径,即:
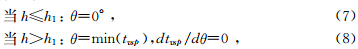
由图 1可见,求取波到达的准确时间很麻烦,对于射线理论不同的位置,射线的路径不一样,如果根据最优的原理求取时间,在层多的时候变得计算量很大,不存在准确值,因此利用射线理论求取波到达的准确时间变得不切实际.我们采用波动方程初至拾取的方法,求取波的时间.
波动方程初至时间拾取的方法很多,最经典的方法就是1985年被提出的能量比法作为地震波初至拾取的的经典方法.该方法在拾取初至时间的时候有很多优点,首先物理意义明确,利用地震道上的能量特征拾取初至时间,其次定义简单明确实际处理中易于实现.与其他方法(如人工拾取,分形分维,神经网络)相比速度较快,易于实现,最重要的是对初至能量较强的地方非常实用,一般初至波的能量都较强所以用这种方法拾取波动方程初至时间比较准确.公式为
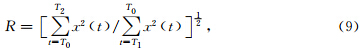
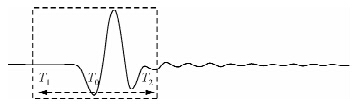 | 图 2 初至拾取示意图 Fig. 2 Schematic diagram of first-arrival picking |
此方法物理意义明确整个时窗都在初至点以前,时窗前后能量主要为仪器噪声,能量比值较小,时窗中心点为初至点时,能量比值为最大值,时窗移入初至后,由于反射波能量变化较小,能量比值也较小.因此,本文采用该方法拾取波动方程的初至时间.下面以多层模型为例,如下图 3~5所示.
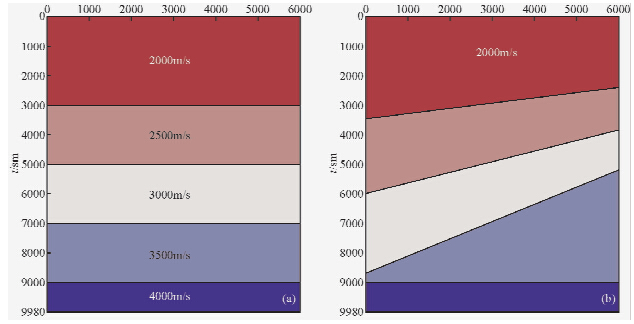 |
图 3 多层模型示意图 (a)平层模型(flat layer);(b)斜层模型(inclined layer). Fig. 3 Schematic diagram of multilayer model |
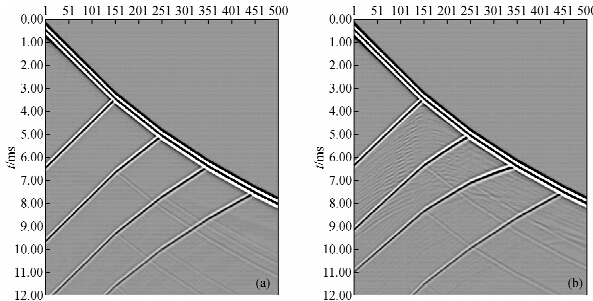 |
图 4 VSP记录 (a)平层的记录(record of flat layer);(b)斜层的记录(record of inclined layer). Fig. 4 VSP record |
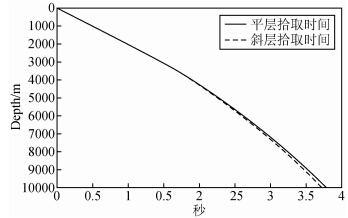 | 图 5 初至拾取时间示意图 Fig. 5 Schematic diagram of first-arrival picking time |
在用VSP记录进行精细标定的时候,经常存在VSP记录与地震记录不一致的情况.此时处理便遇到了困难,是以VSP记录为准呢,还是以地震记录为准.通常的处理过程是以VSP记录为准,将地震记录人为的用VSP记录进行标定.但是从初至拾取的过程中我们可以看到,当地下介质为倾斜的时候VSP记录的初至拾取时间不一样,如果把此时的VSP记录当做时深转化的尺子,此时就会引起VSP记录与地震记录不一致的情况.具体做法为:
(1)建立模型进行VSP正演模拟;
(2)根据初至拾取的时间拾取初至时间;
(3)建立的模型用褶积做当做地震记录;
(4)根据波动方程拾取的初至记录当做VSP记录;
(5)进行归一化将地震记录与VSP记录放在一起显示.
以多层模型为例建立模型(如图 6和图 7所示),然后进行波动方程正演模拟,根据初至拾取的原理,拾取初至时间,通过地面地震对比,当地下介质为水平时候我们地面地震与时深关系重合,当地下为斜层的时候地面地震记录与时深关系一一对应,时深关系存在上移的现象,实际中需要对其进行校正.
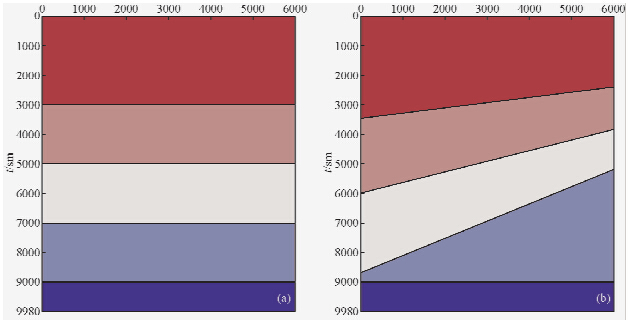 |
图 6 建立模型 (a)平层模型(flat layer);(b)斜层模型(inclined layer). Fig. 6 Established Model |
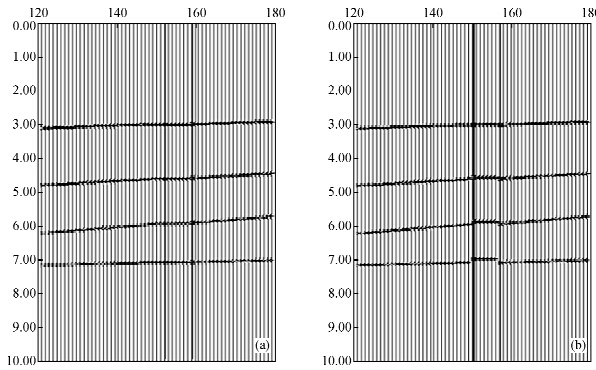 |
图 7 时深关系校正图 (a)校正后(Corrected);(b)校正前(Correct). Fig. 7 Diagram of time-depth relationship correction |
由多层模型得到的时深关系与地震记录进行对比,可以得到如下结论:当地下介质是平层的时候,地震记录与时深关系能够完全对上.但地下介质通常为斜层,此时时深关系与地震记录对不上,时深关系存在上移的现象,此时用标定的时候需要对时深关系进行拉伸或者压缩,使得地震记录与时深关系能够进行对比.
3 软件研制及实际资料处理
在方法研究成果的基础上,采用面向对象技术,基于图形用户接口标准,由数据平台和GUI平台组成的应用开发平台基础之上开发了VSP时差分析校正软件系统,最终形成性能稳定可靠、功能完善、完全自主研发的软件系统,为储层预测及地震解释提供了新的技术平台.
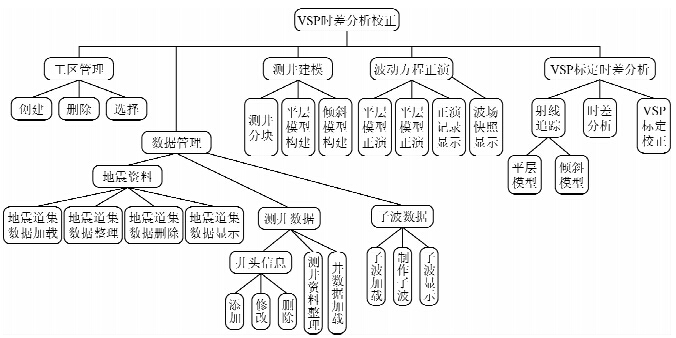 | 图 8 VSP时差分析校正软件系统应用模块结构图 Fig. 8 Structure diagram of application module on software system of time-difference analysis correction |
根据测井曲线,依据最小速度差和最小厚度原理,将测井曲线分成几个层,然后进行波动方程正演得到VSP正演记录,然后根据初至拾取的原理,得到VSP初至拾取的时间.然后进行倾斜时差校正,最后校正旅行时间,使得VSP记录与地面地震记录对应起来.也可以根据时深关系,将地面地震数据由时间域变换到深度域,然后在深度域的地震数据中每层取两个点建立深度域的模型,其余的步骤和根据测井曲线建立模型后的进行的步骤一样,具体的流程图如图 9所示.
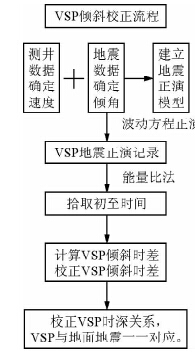 | 图 9 实际处理流程图 Fig. 9 The actual processing flow chart |
首先根据测井曲线,依据最小速度和最小速度差的原理,将测井曲线分层,其次将分的层添加速度,利用地震数据确立地层倾角变成用于地震正演的模型,然后进行波动方程正演模拟,经初至拾取后,得到地震记录与VSP记录进行对比.最终实际处理的时候,使得地震记录与VSP记录能够相一致,便于进行解释.
3.2 倾斜地层VSP时差校正建立模型,然后进行波动方程正演模拟,根据初至拾取的原理,拾取初至时间,通过地面地震对比,当地下介质为水平时候我们地面地震与时深关系重合,当地下为斜层的时候地面地震记录与时深关系一一对应,时深关系存在上移的现象,实际中需要对其进行校正.
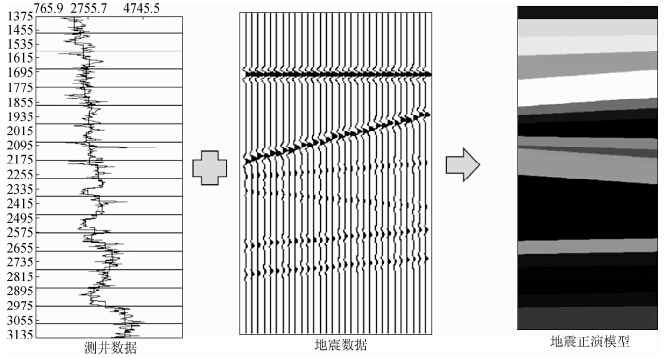 | 图 10 根据测井数据和地震数据建立模型 Fig. 10 The established model with well and seismic data |
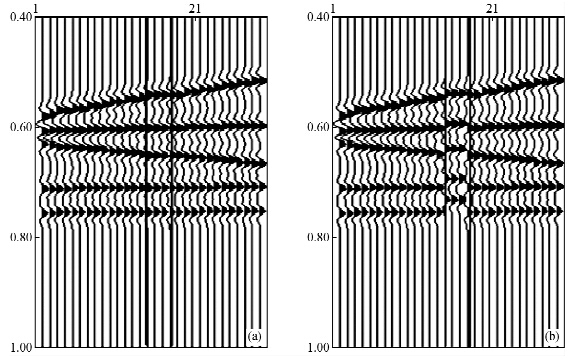 |
图 11 时深关系校正图 (a)校正后(Corrected);(b)校正前(Correct). Fig. 11 Diagram of time-depth relationship correction |
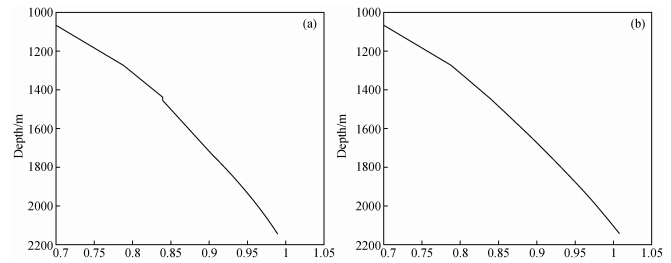 |
图 12 时深关系校正曲线(左图校正前,右图校正后) (a)校正前(Correct);(b)校正后(Corrected). Fig. 12 Curve of time-depth relationship correction(L:Corrected,R:No Correct) |
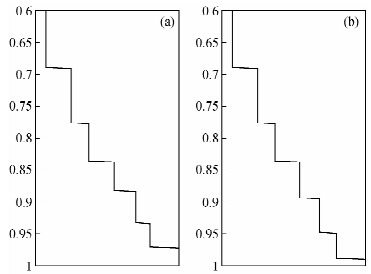 |
图 13 层位标定 (a)校正前(Correct);(b)校正后(Corrected). Fig. 13 Horizon calibration |
由实际模型得到的时深关系与地震记录进行对比,可以得到如下结论,当地下介质是平层的时候,地震记录与时深关系能够完全对上.但地下介质通常为斜层,此时时深关系与地震记录对不上,时深关系存在上移的现象,此时用标定的时候需要对时深关系进行拉伸或者压缩,使得地震记录与时深关系能够进行对比.
时深关系校正后,便得到正确的时间深度关系,然后把这个时间深度关系用于实际的测井数据中,然后根据地震的分层,便可以将实际层位与测井数据能一一对应,下面就是用时深关系对层位进行校正的结果.
4 结论与认识
倾斜地层的存在导致时深关系不准确,关于时深关系很难用统一的解析表达式表示,特别是对于多层介质的情况.因此采用基于高阶有限差分数值模拟的方法实现VSP正演模拟,利用初至拾取得到时深关系.通过倾斜地层和平层地层的对比分析时深关系时差来源,定量分析VSP走时误差.通过时深关系校正实现VSP记录与地面地震精确标定.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部老师的帮助.| [1] | Chen Q L, Yang Z L. 2006. Exploration techniques in lithologic reservoirs[J]. Natural Gas Geoscience (in Chinese), 17(5): 622-626. |
| [2] | Chen S C, Wang H C, Chen L. 2012. A high efficient super-gather migration method for 3D VSP data[J]. Chinese Journal of Geophysics (in Chinese), 55(1): 232-237, doi: 10.6038/j.issn.0001-5733.2012.01.022. |
| [3] | Du J, Wang S X, Liu G C, et al. 2009. VSP wavefield separation using local slopes attribute[J]. Chinese Journal of Geophysics (in Chinese), 52(7): 1867-1872. |
| [4] | Fang W B, Chen L. 2006. Wave equation of prestack depth migration of 3-D VSP data[J]. Geophysical Prospecting for Petroleum (in Chinese), 45(5): 527-531. |
| [5] | Gao L, Chen W C, Wang B L, et al. 2013. Zero-offset VSP wavefield separation using two-step SVD approach[J]. Chinese Journal of Geophysics (in Chinese), 56(5): 1667-1675, doi: 10.6038/cjg20130524. |
| [6] | Guo N M, Wu G C. 2012. Forward-modeling and feasibility study of non-repeating acquired time-lapse seismic exploration[J]. Progress in Geophysics (in Chinese), 27(1): 232-245, doi: 10.6038/j.issn.1004-2903.2012.01.026. |
| [7] | Hao S L, Zhao Q. 2008. Physical modeling research for the effect of lateral velocity on structural imaging[J]. Geophysical Prospecting for Petroleum (in Chinese), 47(1): 49-54. |
| [8] | He R Q. 2006. Wave equation interferometric migration of VSP data[D]. Utah: The University of Utah. |
| [9] | He R Q, Hornby B, Schuster G T. 2007. 3D wave-equation interferometric migration of VSP free-surface multiples[J]. Geophysics, 72(5): S195-S203. |
| [10] | Hornby B, Yu J H. 2007. Interferometric imaging of a salt flank using walkaway VSP data[J]. The Leading Edge, 26(6): 760-763. |
| [11] | Huang Z Y, Qu S L, Wang Y J, et al. 2008. Kirchhoff prestack time migration of PS-wave data for the layered anisotropic medium[J]. Chinese Journal of Geophysics (in Chinese), 52(12): 3109-3115. |
| [12] | Jiang B H, Shen Z H, Zhang P P, et al. 2012. VSP time-depth calibration in tilted stratum[J]. Oil Geophysical Prospecting (in Chinese), 47(4): 598-603. |
| [13] | Li Q Z, Zhang J. 2006. Exploration Method of Lithological Oil And Gas Field (in Chinese)[M]. Qingdao: China Ocean University Press. |
| [14] | Li W Z, Wang P J, Zhang G C, et al. 2011. Researches on time-depth conversion of deep-seated basal strata of Pearl River Mouth basin[J]. Chinese Journal of Geophysics (in Chinese), 54(2): 449-455, doi: 10.3969/j.issn.0001-5733.2011.02.023. |
| [15] | Liu H H. 2004. On accurately acquiring time-depth relationship using VSP data[J]. Well Logging Technology (in Chinese), 28(4): 622-626. |
| [16] | Liu S W, Wang H Z, Chen S C, et al. 2012. Joint imaging method of VSP upgoing and downgoing reflection wave[J]. Chinese Journal of Geophysics (in Chinese), 55(9): 3126-3133, doi: 10.6038/j.issn.0001-5733.2012.09.030. |
| [17] | Meng E, Mu F M, Zhao Y Q, et al. 2005. Dip-moveout-correction (DMO) for VSP corridor stack[J]. Oil Geophysical Prospecting (in Chinese), 40(6): 700-702. |
| [18] | Sun W B, Sun Z D. 2010. VSP reverse time migration based on the pseudo-spectral method and its applications[J]. Chinese Journal of Geophysics (in Chinese), 53(9): 2196-2203, doi: 10.3969/j.issn.0001-5733.2010.09.020. |
| [19] | Wang B L, Zhu G M. 2009. Dip analysis and DMO correction of strata in zero-offset VSP data[J]. Oil Geophysical Prospecting (in Chinese), 44(3): 282-287. |
| [20] | Wang C L, Liu F G, Li Y M. 1996. Dip-moveout correction of VSP data[J]. Oil Geophysical Prospecting (in Chinese), 31(1): 35-40. |
| [21] | Wang Y G, Wang Y C, Wei X C, et al. 2008. Improvement of non-zero offset VSP imaging method[J]. Oil Geophysical Prospecting (in Chinese), 43(6): 641-644. |
| [22] | Wu S P, Huang L Z, Hu T Y. 2011. Multiple reflection imaging by using walkaway VSP data[J]. Geophysical Prospecting for Petroleum (in Chinese), 50(2): 115-123. |
| [23] | Zhang B, Fang W B, Kong X N, et al. 2008. Effect of velocity variation on seismic wave propagation in near surface[J]. Progress in Exploration Geophysics (in Chinese), 31(5): 357-362. |
| [24] | Zhang G Z, Liu H, Yin X Y, et al. 2011. Collation method research of acoustic logging data in seismic interpretation[J]. Progress in Geophysics (in Chinese), 26(6): 25-26, doi: 10.3969/j.issn.1004-2903.2011.06.021. |
| [25] | Zhang M Z, Tan M Y, Wang X M. 2005. Combined describing techniques of tertiary hidden hydrocarbon reservoir in Jiyang depression[J]. Progress in Geophysics (in Chinese), 20(1): 42-48, doi: 10.3969/j.issn.1004-2903.2005.01.009. |
| [26] | Zhang Z G, Li R, Yang J, et al. 2010. Application of non zero offset VSP technology to oilfields with complex faults exploitation[J]. Progress in Geophysics (in Chinese), 25(1): 42-47, doi:10.3969/j.issn.10042903.2010.01.008. |
| [27] | 陈启林, 杨占龙. 2006. 岩性油气藏勘探方法与技术[J]. 天然气地球科学, 17(5): 622-626. |
| [28] | 陈生昌, 王汉闯, 陈林. 2012. 三维VSP数据高效偏移成像的超道集方法[J]. 地球物理学报, 55(1): 232-237, doi: 10.6038/j.issn.0001-5733.2012.01.022. |
| [29] | 杜婧, 王尚旭, 刘国昌,等. 2009. 基于局部斜率属性的VSP波场分离研究[J]. 地球物理学报, 52(7): 1867-1872. |
| [30] | 方伍宝, 陈林. 2006. 三维VSP资料波动方程叠前深度偏移研究[J]. 石油物探, 45(5): 527-531. |
| [31] | 高磊, 陈文超, 王保利,等. 2013. 基于两步SVD变换的零偏VSP资料上下行波场分离方法[J]. 地球物理学报, 56(5): 1667-1675, doi: 10.6038/cjg20130524. |
| [32] | 郭念民, 吴国忱. 2012. 非重复采集时移地震正演模拟及可行性分析[J]. 地球物理学进展, 27(1): 232-245, doi: 10.6038/j.issn.1004-2903.2012.01.026. |
| [33] | 郝守玲, 赵群. 2008. 横向速度变化对构造成像影响的物理模拟研究[J]. 石油物探, 47(1): 49-54. |
| [34] | 黄中玉, 曲寿利, 王于静,等. 2008. 层状各向异性介质转换波克希霍夫叠前时间偏移[J]. 地球物理学报, 52(12): 3109-3115. |
| [35] | 姜本厚, 沈章洪, 张平平,等. 2012. 倾斜地层的VSP时深标定研究[J]. 石油地球物理勘探, 47(4): 598-603. |
| [36] | 李庆忠, 张进. 2006. 岩性油气田勘探[M]. 青岛: 中国海洋大学出版社. |
| [37] | 李伍志, 王璞珺, 张功成,等. 2011. 珠江口盆地深部基底地层的地震时深转换研究[J]. 地球物理学报, 54(2): 449-455, doi: 10.3969/j.issn.0001-5733.2011.02.023. |
| [38] | 刘海河. 2004. 准确求取VSP时间-深度关系的探讨[J]. 测井技术, 28(4): 622-626. |
| [39] | 刘守伟, 王华忠, 陈生昌,等. 2012. VSP上下行反射波联合成像方法研究[J]. 地球物理学报, 55(9): 3126-3133, doi: 10.6038/j.issn.0001-5733.2012.09.030. |
| [40] | 孟恩, 牟风明, 赵彦青,等. 2005. VSP走廊叠加倾角时差校正[J]. 石油地球物理勘探, 40(6): 700-702. |
| [41] | 孙文博, 孙赞东. 2010. 基于伪谱法的VSP逆时偏移及其应用研究[J]. 地球物理学报, 53(9): 2196-2203, doi: 10.3969/j.issn.0001-5733.2010.09.020. |
| [42] | 王保利, 朱光明. 2009. 零井源距VSP数据地层倾角分析和倾角时差校正[J]. 石油地球物理勘探, 44(3): 282-287. |
| [43] | 王成礼, 刘富贵, 李幼铭. 1996. VSP倾角时差校正方法[J]. 石油地球物理勘探, 31(1): 35-40. |
| [44] | 王玉贵, 王彦春, 魏修成,等. 2008. 非零井源距VSP成像方法的改进[J]. 石油地球物理勘探, 43(6): 641-644. |
| [45] | 吴世萍, 黄录忠, 胡天跃. 2011. Walkaway VSP多次波成像技术研究[J]. 石油物探, 50(2): 115-123. |
| [46] | 张兵, 方伍宝, 孔祥宁,等. 2008. 近地表速度变化对地震波传播的影响[J]. 勘探地球物理进展, 31(5): 357-362. |
| [47] | 张广智, 刘洪, 印兴耀,等. 2011. 地震解释中声波测井资料的整理方法研究[J]. 地球物理学进展, 26(6): 25-26, doi: 10.3969/j.issn.1004-2903.2011.06.021. |
| [48] | 张明振, 谭明友, 王兴谋. 2005. 济阳坳陷第三系隐蔽藏储层预测配套技术[J]. 地球物理学进展, 20(1): 42-48, doi: 10.3969/j.issn.1004-2903.2005.01.009. |
| [49] | 张振国, 李瑞, 杨军,等. 2010. 非零偏VSP技术在油田复杂断块开发中的应用[J]. 地球物理学进展, 25(1): 42-47, doi:10.3969/j.issn.10042903.2010.01.008. |
 2014, Vol. 29
2014, Vol. 29

