2. 中国石油集团测井有限公司技术中心, 西安 710077
2. Technology Center, CNPC LOGGING CO., LTD, Xi'an 710011, China
介电测井是利用岩石介电常数(ε)区分不同岩层的一组测井方法的统称(张庚骥,1989).基本工作原理为:由一个发射线圈发射电磁波,测量两个接收处感应线圈处感应电动势的幅度衰减A和相位差Δφ.然后,通过求解(A,Δφ,ε,σ)组成的非线性方程组解出介电常数和电导率.由于地层岩石骨架的介电常数较为稳定,储集层中所含流体(水、油、气)的介电常数差异很大;介电测井数据能够较好地判别地层中的水层和油层.此外,介电测井可获得地层的介电常数和电导率,可以应用于油层和水层同为低阻或高阻的情况,也可用于油田开发过程中注入水情况下的测量,不受泥浆和套管绝缘性的影响.
在我国电磁波测井的研究和开发始于20世纪60年代,并取得一系列的成果(邢光龙等, 2001,2002;冯国庆等,2002;刘四新,佟文琪,2004;赵媛,2011;汪宏年,2012;仵杰,2013),但也存在一些列问题.主要研究了复杂地层对电磁波测井响应的影响.赵媛等采用数值仿真技术研究了随钻电磁波电阻率测井仪器线圈系参数(赵媛,2011);丁晓林等利用有限元方法分析了工作频率为400 kHz~2 MHz的随钻电磁波电阻率测井响应特征(丁晓林,2012);张雷等利用数值匹配法分析了横向各向同性地层对倾斜线圈系响应的影响(张雷,2012);范宜仁等利用积分法研究了倾斜各向异性地层随钻电磁波电阻率测井的响应特征(范宜仁,2013);李亭亭等利用井地电磁法研究了影响勘探深度的各种因素(李亭亭,2013).由于所用电磁波频率低(小于2 MHz),测量的电磁波的幅度衰减和相位差主要反映地层的电导率,而不反应介电信息.虽然它的测深度较大,但纵向分辨率一般不高,在剩余油测井和薄层测井方面有很大的局限性.而频率为200 MHz以上的超高频电磁波传播测井具有很高的纵向分辨能力,但探测深度太浅,基本上只能反映侵入带介电常数的信息,且其测量结果受井壁不规则的影响非常大.因此,介电测井仪应采用多种工作频率(几十MHz~几百MHz),介电响应才可同时反映介质的电阻率和介电信息.国外各大测井公司都推出了商用的介电测井仪器,其中应用最广泛的是斯伦贝谢公司的介电扫描成像测井仪-Dielectric Scanner.由于技术保密,仪器的各项参数不对外公布,所以本文利用数值方法来研究介电测井仪的各项工作参数,以期对介电测井仪器的研制提供理论指导和数据支撑.
张庚骥给出了在均质地层中(A,Δφ),关于频率,f接发收器间距L,接收器间距ΔL,介电常数ε电导率σ在复数域上的非线性方程组(张庚骥,1989).柯式镇等比较了用平面波模型、球面波模型和混合波模型由电磁波传播测井幅度比和相位差计算介电常数的算法(柯式镇等,2005).刘国强根据Lambert W函数的性质将形式复杂的非线性方程转化成了形式简单的非线性方程(刘国强,2000),利用牛顿迭代法求出(ε,σ).但牛顿迭代法只在真值附近有较好的收敛性和收敛速度,即对初值的选择要求很高,选择不当会出现数值发散,得不到真值.本文采用球面波模型,数值计算了几种典型地层的介电响应特性,从频率、源距的变化规律,分析确定了介电测井仪器的工作频率,最大和最小源距等参数的选择范围;同时,对刘国强得到的形式简单的非线性超越方程进一步求解,得到了(ε,σ)关于(A,Δφ)的解析表达式,并进行编程计算,得到了精度极高的解,为进一步开发介电扫描成像测井仪提供理论支撑. 1 介电测井仪器工作参数的确定
当发射线圈和接收线圈缩成点状,且两者的间距远大于线圈的尺寸的时候,可将发射的电磁波看作为球面波(张庚骥,1989).张庚骥给出了在均质地层中,(A,Δφ)关于频率f,接发收器间距L,接收器间距ΔL,介电常数ε电导率σ在复数域上的非线性方程组.下面根据该响应方程组讨论在给定地层中介电响应随频率和接发收器间距的变化规律.表 1是几种典型地层的电参数.
|
|
表 1 几种典型地层的电参数 Table 1 Electrical parameters of several typical formation |
当L1=0.095 m,L2=0.12 m时,计算并绘制出在上表中四种地层下介电响应和频率的关系,如图 1,2所示.
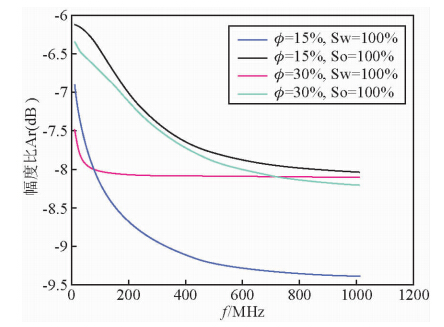 | 图 1 砂岩两种孔隙度下饱含水和石油时幅度比和频率的关系 Fig. 1 The relationship between the amplitude ratio and frequency in s and stone of two kinds of porosity saturated with water or oil |
由图 1和图 2可知,对于给定地层随着频率的增大,幅度比在增大;但当频率大于300 MHz时,对于给定的四种地层,介电响应中幅度比几乎不随频率变化或变化幅度很小,此时频率对幅度比几乎无贡献,即球面波模型只适用于频率低于300 MHz的情况.这是因为引起幅度衰减的主要原因是介质自身对电磁波能量的吸收作用,此时电磁波自身的性质特点(频率,波形)对幅度衰减的影响就很小了.
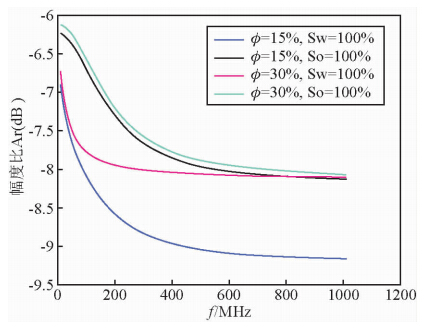 | 图 2 石灰岩两种孔隙度下饱含水和石油时幅度比和频率的关系 Fig. 2 The relationship between the amplitude ratio and frequency in limestone of two kinds of porosity saturated with water or oil |
石庆东指出,幅度衰减和相移均随频率的增大而增大(石庆东等,2000),这和图 1,2揭示的规律是相一致的.频率越高、接发收器间的距离越大,幅度衰减和相位差也会越大.为了使仪器能接收到较强的信号,下面研究此模型适用的最高频率300 MHz时,介电响应和接发器间距L的关系,以确定接发器间的最大距离.
由砂岩和石灰岩在两种孔隙度下,饱含水时的情况可以看出,当L=150 mm时,在频率为300 MHz时衰减最大为-60~-70 dB,衰减就很严重了,相位差达到了800°左右,信号延迟严重;为了信号的准确测量,建议介电测井仪器的最大接发器间的最大距离不超过0.15 m.斯伦贝谢公司的介电扫描成像测井仪的最大源距为120 mm,和本文得到的结论是相符的.
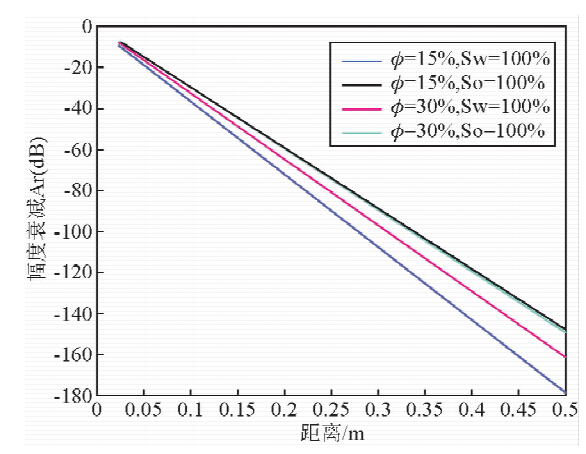 | 图 3 300 MHz砂岩两种孔隙度下饱含水和石油时最大衰减和距离的关系 Fig. 3 The relationship between peak attenuation and distance in s and stone of two kinds of porosity saturated with water or oil under 300 MHz |
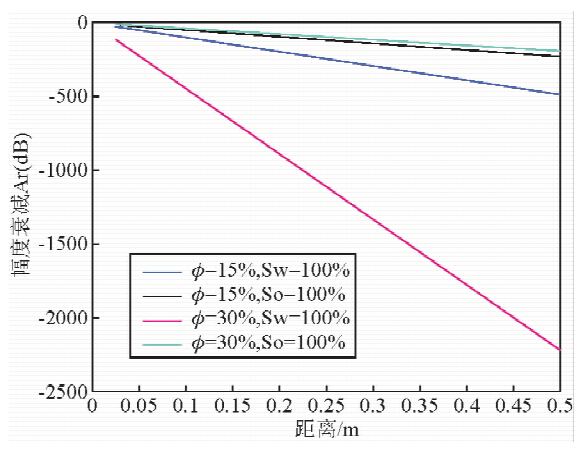 | 图 4 300 MHz砂岩两种孔隙度下饱含水和石油时最大相移和距离的关系 Fig. 4 The relationship between maximum phase shift and distance in s and stone of two kinds of porosity saturated with water or oil under 300 MHz |
因为介电探测器的相位分辨率有限,当接发收器间的距离很小时,相位偏移会很小,导致仪器测不出相位差,所以要研究接发收器间的最短距离.介电响应随频率、电导率、介电常数的增大而增大,所以应研究电参数较小的地层对相位的影响.下面就以孔隙度Φ=30%,So=100%的石灰岩和Φ=15%,So=100%的砂岩为例,研究其在20 MHz下的相位随距离变化特性.
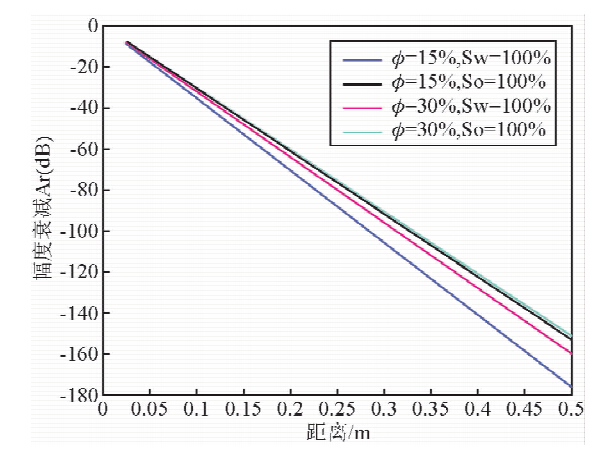 | 图 5 300 MHz石灰岩两种孔隙度下饱含水和石油时最大衰减和距离的关系 Fig. 5 The relationship between peak attenuation and distance in limestone of two kinds of porosity saturated with water or oil under 300 MHz |
由图 7可以看出,随着接发收间距的增大,相位差在变大.但是在所选地层中,由于电导率和介电常数较小,所以相位差也比较小,这就要求仪器要具有较高的相位分辨率.在源距为45 mm时,两种地层的介电响应分别为0.06°和0.24°.为了使仪器能够精准测量和计算的高精度,一般都选择最小源距在50 mm左右,Dielectric Scanner的最小源距是45 mm.
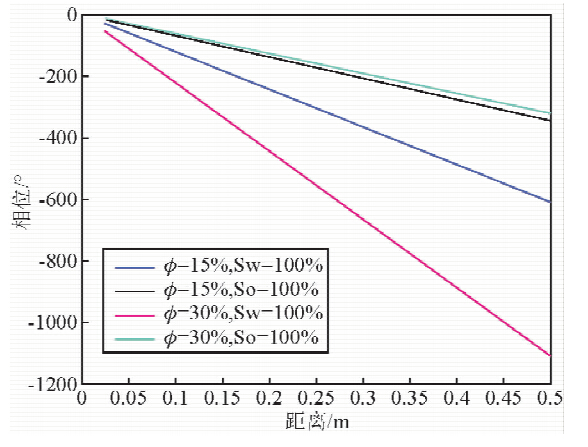 | 图 6 300 MHz石灰岩两种孔隙度下饱含水和石油时最大相移和距离的关系 Fig. 6 The relationship between maximum phase shift and distance in limestone of two kinds of porosity saturated with water and oil or 300 MHz |
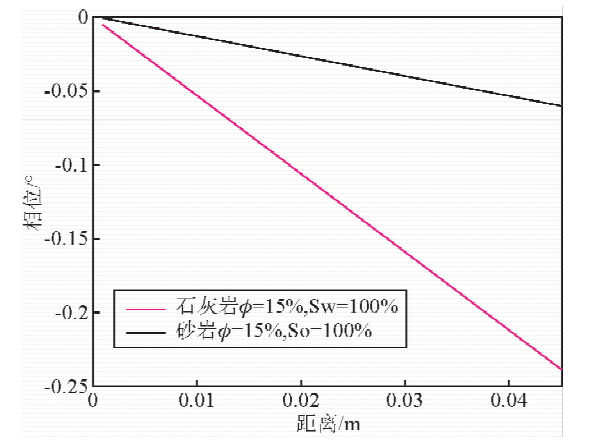 | 图 7 20M时两种地层下相位差和间距的关系 Fig. 7 The relationship between the phase difference and the distance in two kinds of formation under 20 MHz |
由文献(张庚骥,1989)可得
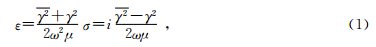
将V1,V2相比并取自然对数,有
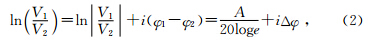
其中,
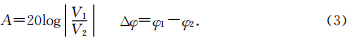
A称为幅度衰减,Δφ为相位差
对球面波公式(张庚骥,1989)进行等价变形得:
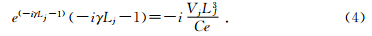
由数学知识可知,在复数域内对于任意的x,满足xex=m时,则有x=W(m),其中W(m)称为Lambert W函数,但在复数域上是多值的.
由(4)式可得到传播常数的表达式为

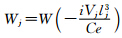 进而可推出
进而可推出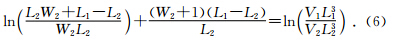
对于式(15)利用MATLAB进行求解可得W2的表达式为
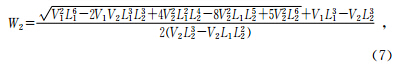
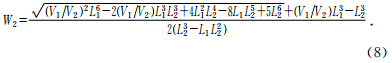
这样由测量出的(V1,V2),利用(8)式可以求出W2,再代入(5)式,求出γ,进而可求出(ε,σ).这其中不涉及迭代运算,避免了线性迭代引起的误差和由于初值选择而引起的方程无解的情况.由式(5),(6)可以看出,Lambert W函数W2只是其中的一个过程参量,不用利用Lambert W函数求解出其对应的x,所以避免了Lambert W函数引起的多值不确定性. 3 数值实验
为了验证方法的可行性和检验其精度,进行数值实验. 采用单发双收仪器模型,发射线圈T和接收线圈R1的距离为0.095 m,和R2的距离为0.12 m.工作频率选择300 MHz.
首先,给定(A,Δφ),对本文给的公式,利用MATLAB软件进行编程计算出(εr,σ).再根据求出的(εr,σ),利用文献(张庚骥,1989)中的响应公式计算,得到响应(A′,Δφ′).对比(A,Δφ)和(A′,Δφ′)以检验本解法的可行性.
由表 2对比(A,Δφ)和(A′,Δφ′),两者之间的绝对误差可控制在10-4以内,可以看出此解法是可行的.
讨论本文提供解法的精确度,仍然采用单发双收仪器模型,给定(εr,σ),利用文献(张庚骥,1989)中的公式计算出(A,Δφ);采用本文解法,得到(ε′ r,σ′),并与文献(刘国强,2000)中的计算结果相比较.表 3为本文所给出的解析解法在给定值上的误差.
从表 3中可以看出本文提出的解法的最大误差分别为(0.0001%,0.000),文献(刘国强,2000)中通过迭代算法求解结果的最大误差为(0.46%,1.00%),传统算法的最大误差为(6.22%,7.00%).从而可以看出本文的解法具有更高的精度.
下面给出σ=0.01,εr在(5-80)内每隔5取点时,本文所提供算法的模拟结果.
从图 8和图 9中看出解析解法解出的电导率σ和介电常数εr的相对误差可控制在千分之一之内,即此解法有较高的精确度.
刘国强等对方程进行了简化,但是求解化简后的非线性方程时,仍然采用了线性迭代算法(Newton-Raphson、BFGS).由于牛顿迭代法对于迭代初值的要求较为严格,否则就会不收敛;其次,每一次迭代都要求计算迭代点的导数值,这势必会增加计算量. 本文所给出的解法,求出了其解析表达式,便于计算和编程,给出的结果更精确,计算速度更快.
4 结 论 综上所述,本文通过对球面波模型中介电响应关于频率、源距的讨论确定了介电测井仪器适合此模型的工作频率 范围为20~300 MHz,最小和最大源距为 150 mm和45 mm,现有仪器的工作间距也都在这一范围内,说明了结果的准确性. 本文利用Lambert W的性质对电磁波模型进行了简化,并得到了形式简单的非线性方程的解析表达式,避免了线性迭代算法带来的种种弊端.提出的方法易于编程计算,计算速度明显加快,且几乎为其精确解,可以实时的将测井信号转换成视介电常数和视电导率.所以此解析解法更适用于求解此测井模型.
![]()
表 2 解法的可行性结果
Table 2 The feasibility of the method
![]()
表 3 解析解法的误差
Table 3 The error of analytic solution
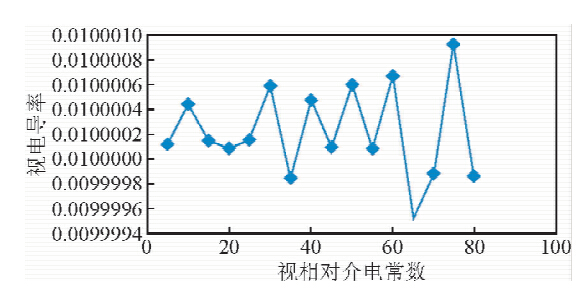
图 8 视电导率σ的误差曲线
Fig. 8 The error curve of the apparent conductivity σ
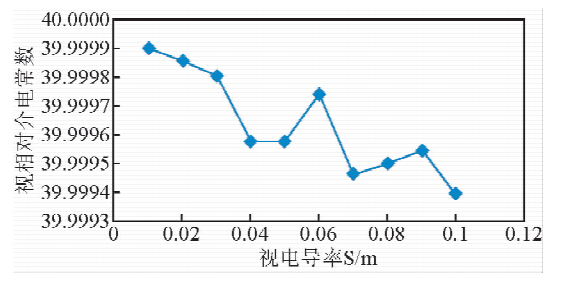
图 9 视介电常数εr的误差计算
Fig. 9 The error curve of the apparent dielectric constant εr
| [1] | Ding X L, Lin C D, Shao C J.2012. Forward simulation based on ANSYS for electromagnetic logging while drilling. Well Logging Technology (in Chinese), 36(5):469-474. |
| [2] | Feng Q G, Liu M F, Liu Y C et al. The theoretical research of high frequency electromagnetic wave logging by symmetrical measurement [J]. Chinese J. Geophys (in Chinese), 45(3): 435-443. |
| [3] | Fan Y R, Hu Y Y, Li H.2013.Numercal simulation of electromagnetic logging response while drilling in anisotropic dipping formation [J]. Well Logging Technology (in Chinese), 37(2):137-142. |
| [4] | Ke S Z, Dai S H, Sun D J et al.2005. On the comparisons between permittivity algorithms in electromagnetic propagation log [J]. Well Logging Technology (in Chinese), 29(5):439-440. |
| [5] | Li T T, Wang J, Zhu K G. Research on the exploration depth of the borehole-surface electromagnetic field [J].Progress in Geophys (in Chinese), 28(1):373-379. doi:10.6038/pg20130141. |
| [6] | Liu G Q, Yang W, Feng Q N, et al. 2000.A new method to simultaneously solve apparent conductivity and apparent dielectric constant in high frequency well-logging[J]. Chinese J. Geophys (in Chinese), 43(3):428- 432. |
| [7] | Liu S X, Tong W Q.2004. The situation and progress of electromagnetic well logging [J]. Progress in Geophys (in Chinese), 19(2):235-237. |
| [8] | Shi Q D, Feng Q N, Shang Z Y.2000. Response characteristics of Dielectric logging [J]. Xinjiang Petroleum Geology (in Chinese),21(5):394-396. |
| [9] | Shi X F, Li Z, Cai Z Q.2002. Investigation depth of MWD propagation resistivity logging [J]. Well Logging Technology (in Chinese), 26(2): 113 -117. |
| [10] | Wang H N,Hu P,Tao H G,et al.Fast algorithm of responses of array multicomponent induction logging tool in horizontally stratified inhomogeneous TI media.Chinese J.Geophys.(in Chinese), 2012,55 (2)717-726.doi:10.6038/j.issn.0001-5733.2012.02.036. |
| [11] | Wu J,Xu L.2013.The response characteristics of the horizontal coil of the three components induction logging in thin layers[J]. Progress in Geophys (in Chinese). 2013,28(4):1935-1942.doi:10.6038/pg20130436. |
| [12] | Xing G L, Liu M F, Yang S D. 2001. The sensitivity analysis and characteristic recognition method of the high frequency electromagnetic wave logging(Ⅰ)—sensitivity analysis[J]. Well Logging Technology (in Chinese),25(5):354-357. |
| [13] | Xing G L, Zhang M L, Liu M F et al. 2002. An inversion of dielectric constant and resistivity by using high frequency electromagnetic wave logging [J]. Geophys (in Chinese), 45(3):435-443. |
| [14] | Yang X Q. 2011. New multiple frequency dielectric scanning imaging logging tool- residual oil and gas discovery[J], Well Logging Technology (in Chinese), 35(1):61. |
| [15] | Zhang G J. 1989. Electrical logging (part ii) [M].Beijing: Petroleum Industry Press (in Chinese). 152-154. |
| [16] | Zhao Y, Dun Y Q, Yuan J S.2011.On coil system design for MWD electromagnetic wave logging tools [J]. Well Logging Technology (in Chinese), 35(3):224-229. |
| [17] | Zhang L, Chen H, Wang X M. 2012. Numerical modeling of responses to a tilted coil antenna in a transversely isotropic formation. Chinese J, Geophys, (in Chinese), 55(10):3493-3505. doi:10.6038/j.issn.0001-5733.2012.10.033. |
| [18] | 丁晓林,林春丹,邵长金.2012.基于ANSYS软件的随钻电磁波测井正演模拟计算[J].测井技术,36(5):469-474. |
| [19] | 冯国庆,刘曼芬,刘迎春,等.2002.对称化测量高频电磁波测井的理论研究[J].地球物理学报,45(3): 435- 443. |
| [20] | 范宜仁,胡云云,李虎,等.2013.倾斜各向异性地层随钻电磁波测井响应模拟[J]. 测井技术,37(2):137-142. |
| [21] | 柯式镇,代诗华,孙德杰,等.2005.电磁波测井计算介电常数算法比较研究[J].测井技术,29(5):439- 440. |
| [22] | 李亭亭,王佳,朱凯光.2013.井地电磁法勘探深度研究[J].地球物理学进展,28(1):373-379. doi:10.6038/pg20130141. |
| [23] | 刘国强,杨韡,冯启宁.2000.高频电磁波测井同时求解视电导率和视介电常数[J].地球物理学报, 43(3):428-432. |
| [24] | 刘四新,佟文琪. 2004.电磁波测井的现状和发展趋势[J].地球物理学进展,19(2):235- 237. |
| [25] | 石庆东,冯启宁,尚作源.2000.介电测井响应特性[J].新疆石油地质,21(5):394-396. |
| [26] | 史晓锋,李铮,蔡志权. 2002.随钻电磁波测量工具探测深度研究[J].测井技术.26 (2) :113- 117. |
| [27] | 汪宏年,胡平,陶宏根等.水平层状非均质横向同性地层中阵列多分量感应测井响应的快速计算[J].地球物理学报.2012,55 (2)717-726.doi:10.6038/j.issn.0001-5733.2012.02.036. |
| [28] | 仵杰,许亮.2013.三分量感应水平线圈系在薄层中的响应特性研究[J].地球物理学进展,2013,28(4):1935-1942.doi:10.6038/pg20130436. |
| [29] | 邢光龙,刘曼芬,杨善德.2001.高频电磁波测井的灵敏度分析与特征识别方法(I)—灵敏度分析[J].测井技术, 25(5):354- 357. |
| [30] | 邢光龙,张美玲,刘曼芬,等. 2002.利用高频电磁波测井反演地层介电常数和电阻率[J].地球物理学报, 45(3):435- 443. |
| [31] | 张庚骥.1989.电法测井(下册) [M]. 北京:石油工业出版社. 152-154. |
| [32] | 赵媛,顿月芹,袁建生.2011随钻电磁波测井仪器线圈系参数设计方法研究[J].测井技术,35(3):224-229. |
| [33] | 张雷,陈浩,王秀明.2012.横向各项同性地层中倾斜线圈系响应特征的数值模拟[J].地球物理学报.55(10):3493-3505.doi:10.6038/j.issn.0001-5733.2012.10.033. |
 2014, Vol. 29
2014, Vol. 29


