随着油气勘探程度的加深,把油藏岩性、应力、裂缝和流体综合进行描述的需求对常规纵波地震勘探提出了挑战,多分量地震勘探可提供更丰富的地震信息,能够完整地记录矢量地震波场,从而减少纵波勘探的多解性,满足勘探开发的需求.多分量资料的叠前偏移技术是多分量勘探技术发展中近几年研究开发的重点,是解决复杂地质、构造成像、油藏描述问题的关键所在(张永刚等,2004;胡天跃等,2004).
传统的多分量资料偏移方法是将检波器接收到的地面记录分解成纵波和转换波记录,然后分别进行成像.尽管纵波、转换波分别成像存在处理成本低、处理方法成熟等优势,但在实际处理中它存在如下三方面问题:
(1)地表波型分离不准确.对于各向同性介质通常假设记录的垂直分量为纵波,水平分量为横波,或者采用偏振分析、τ-p变换等方法在地表分解波场,但地下传播的地震波场是耦合的,目前已发展的波场分离方法基本上都难以达到纵横波的完全分离.
(2)忽略了波场的矢量性质.多分量地震资料记录的是矢量波场,采用先波场分离,然后基于标量偏移方法对纵波和转换波分别偏移的做法消除了多分量地震波场的部分信息,无法完全反映波在地下介质中的传播规律和特点.
(3)不利于后续分析和解释.由于纵横波偏移结果通常不能连续对齐,还需要借助手动图像配准等技术进行成像后处理(Dellinger等,1990;谢飞等,2008;冯晅等,2011;李志远等,2013).为避免上述问题,可通过矢量波成像技术探讨多分量资料的叠前偏移,即通过直接求解全弹性波动方程重建矢量波场,以此保持多分量资料的矢量性质,从而更逼近波在地下介质传播的实际情况.矢量波成像方法与纵波成像方法类似,有基于射线的Kirchhoff积分方法和基于波场延拓的单程波波动方程方法和双程波波动方程方法,在此方面做出研究和贡献的学者有: Chang和McMechan(1994)推导了差分格式弹性波逆时偏移方法,Kuo和Dai(1984)对炮域弹性波Kirchhoff偏移作了较深入的研究,Hokstad(2000)实现了观测沉降弹性波Kirchhoff偏移,Sun和McMechan(2001)研究了标量算子对弹性波成像的技术,底青云和王妙月(1997)、张美根和王妙月(2001)等采用有限元方法研究各向异性弹性波逆时偏移,何兵寿和张会星(2006)、杜启振和秦童(2009)等对多分量资料矢量法逆时偏移进行了研究.
基于波场延拓的成像方法主要包括两步:
(1)重建震源波场和检波点波场,其中检波点波场的重建是把多分量数据作为弹性波动方程数值解的边界条件进行数值求解实现.
(2)使用成像条件从重建波场提取成像信息进行成像,这是矢量波成像的关键问题.一般的互相关成像条件的做法是将两个波场对应坐标分量进行两两互相关运算,但对于矢量波场而言,由于每个分量都是包含未分解波场的混合波场,因而会导致产生串扰噪音(例如震源波场的垂向分量包含主要纵波和部分横波剩余,剩余波场与检波点波场错误的互相关对偏移结果造成干扰)(Yan and Sava, 2008).为解决此问题,可采用波型分解获取纯波型波场,再构建波型分量互相关成像条件来取代初始坐标轴分量的互相关.纯波型分量互相关成像结果可代表单一波型在物理性质分界面的反射信息,因此成像信息简洁明了并利于后续地震资料的解释(王娟等,2012).关于纵横波场的分解已有如下研究: Dellinger和Etgen(1990)提出极化投影法来获得TI介质中纯的纵横波场;Yan和Sava(2011)对此方法进行改进并将其扩展到非均匀介质,在倾斜对称轴横向各向同性TTI介质中有效实现了纵横波场的分解.
本文首先从各向异性弹性波动方程出发,将弹性波的逆时延拓转化为边值问题,并将差分方程求解域使用交错网格进行剖分,从而推导出空间高阶弹性波逆时传播差分格式;接下来,本文通过分析矢量波场特点指出纯波型互相关成像条件是最恰当的选择;然后针对TI介质的局部特征提出了沿极化矢量方向投影分离纵横波的策略,最终得到稳定的分离算子.该分离算子考虑了介质局部性质和倾角变化,可以适应介质的复杂性,模型试算表明该方法比传统基于散度和旋度分离的效果更彻底,将此分解方法应用于矢量波逆时偏移成像不但可以提高成像精度,还可以输出正确反映地下反射系数的成像结果,利于后续资料的解释.
1 方法原理 1.1 一阶弹性波方程离散化在二维TTI介质中,设体力为零,则一阶速度-应力弹性波波动方程可表示为
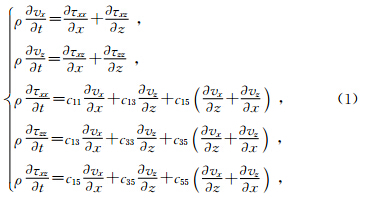
其中τij为应力分量,vi为速度分量,ckl为弹性常数,ρ为弹性体密度(Virieux,1986).
由差分格式使用的网格参数定义,可对弹性波速度-应力方程(1)进行高阶交错网格离散化.根据Taylor公式展开,得到2阶精度的时间差分近似表示,然后通过下式计算方程(1)中一阶空间导数2N阶空间差分精度的差分格式(董良国,2000;Moczo et al., 2007):
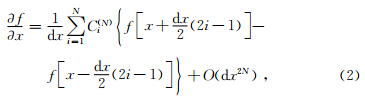
方程(2)中差分权系数Ci(N)的准确求取是确保一阶空间导数2N阶差分精度的关键,由Taylor展开可确定Ci(N)有如下取值:

可计算得当N=4时,C1(4)= 1225 1024,C2(4)= 245 3072,C3(4)= 49 5120,C4(4)= 5 7168 .
设速度和应力的离散值分别是
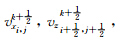
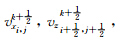 ,令dx=dz,则方程(1)第一个公式高阶空间精度的差分格式为
,令dx=dz,则方程(1)第一个公式高阶空间精度的差分格式为
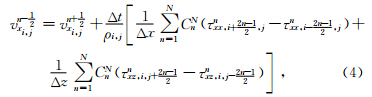
同理可得方程(1)中其他四个方程的差分格式(夏凡等,2004;李博等,2012).
1.2 矢量成像条件
矢量波场的互相关成像条件需要在所有分量上实现,其中每个分量都是包含纵波和横波的混合波场.若直接由坐标分量互相关进行成像,偏移结果不仅会产生串扰噪音,同时也不利于对PP或PS反射等纯波型成像进行解释,因此先将矢量波场分解为纯的纵横波场,再利用纯波型分量做互相关运算则可以有效避免上述问题,是矢量波成像的优选成像条件.其表达形式(Yan and Sava,2008)为
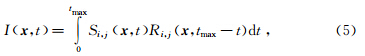
其中I x,t 代表成像结果,Si,j x,t和Ri,j x,t 分别表示震源波场的纯波型分量(P-和SV-)和检波点波场纯波型分量(P-和SV-).
我们知道,对于各向同性介质来说,求取矢量波场的散度与旋度即可分别代表波场的纵波和横波分量.但对于TI介质,这种分离方法不够准确,下一节我们将进一步研究TI介质的纵横波分离方法.
1.3 波型分解原理任意矢量波场可由Helmholtz分解得到一个标量位和一个矢量位,故矢量波场 W 可由下式分解为一个无旋标量位Θ和一个无散矢量位 Φ :

通过上式对矢量波场分别应用算子 Δ ·和Δ ×进行运算,从而得到它的标量与矢量分量为

对于各向同性弹性介质远场震源,物理量P和S分别表示纵波与横波波场.在空间域可将(7)中第一个式子表示为
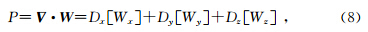
其中Dx,Dy,Dz分别表示x,y和z方向的导数,在波数域中,这些算子可分别表示为ikx,iky,ikz,故上式在波数域中的等价表达式为
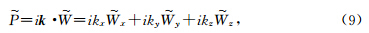
其中 k ={kx,ky,kz}代表波矢量,W ~(kx,ky,kz)代表波场 W(x,y,z)的三维傅氏变换.此式可以看作在傅氏域中通过算子i k ·把波场 W(x,y,z)投影到了波矢量 k 方向(纵波的极化方向)上得到纵波;同理类似,通过算子i k ×把波场投影到波矢量的正交方向(横波的极化方向)可得到转换横波.图 1a所示为各向同性介质模型中纵波极化矢量方向,函数变量分别为归一化的kx与kz,由于在各向同性介质中纵波与波矢量沿相同方向,因此极化矢量方向如图呈辐射状(Yan and Sava, 2008).
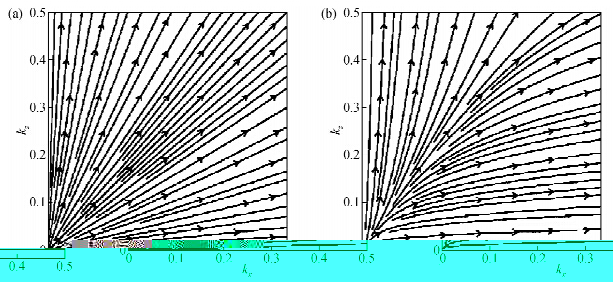 | 图 1(a)各向同性介质中极化矢量方向呈辐射状;(b)各向异性介质中极化矢量方向呈弯曲状. Fig. 1(a)Polarization vectors radiate from origin in isotropic medium;(b)Polarization vectors present bending in anisotropic medium. |
若将同样的理论扩展到各向异性介质,为得到准纵波需将波场投影到真正的极化方向 U 上,只需把波场分解方程(9)改进(Dellinger and Etgen,1990)为
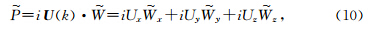
U(kx,ky,kz)代表各向异性介质中的极化矢量方向,此时准纵波极化矢量方向与波矢量 k 方向不同,如图 1b所示为各向异性介质中准纵波的极化矢量方向,其中变量kx和kz的范围从0到0.5变化,由图可见极化矢量不再呈辐射状,这是因为在各向异性介质中,极化矢量与波矢量并不总是沿相同方向(仅在对称面上和沿对称轴方向相同).式(10)在空间域中的等价表达式可写为
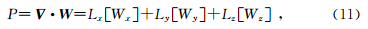
其中Lx,Ly,Lz表示iUx,iUy,iUz的逆傅氏变换,L[·]表示空间褶积,Wx,Wy,Wz分别为各向异性介质中x,y,z方向的逆导数算子,它们是随位置变化的介质参数的函数.由Christoffel方程可求得极化矢量 U(k)为

其中 G 为Christoffel矩阵,cijkl代表弹性系数,nj,nl分别为在j和l方向的标准化的波矢量,i,j,k,l=1,2,3,参数V是矩阵 G 的特征值,它代表每个波场的相速度,是波矢量 k 的函数.在VTI介质垂向对称面上,方程(12)写为
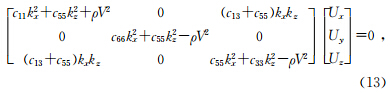
给定介质模型的弹性系数和密度,由此式可计算极化矢量 U(k)的分量(矩阵G 的特征值).
对于任意各向异性的介质,通过解Christoffel方程能够得到极化矢量.而对于在TTI介质一个对称面上传播的平面波,由于qP波与qSV波是和qSH波解耦的,且其极化方向在对称面上(Yan and Sava, 2008,2011).因此可将ky设为0,求得:
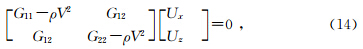
其中
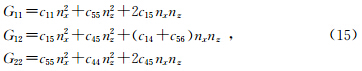
给定介质中网格点的刚度张量,即可由上式计算P波和SV波的极化矢量 U P={Ux,Uz}和U S={-Uz,Ux},最后将波场分量分别投影到极化矢量方向上即可实现TI介质矢量波场的纵横波分解.
2 实验与讨论 2.1 纵横波分解基于极化矢量投影法分解波场依赖介质的局部性质,可应用于TI介质的纵横波分解.为探讨其精确性,我们把极化矢量法与Helmholtz分解法的数值模拟结果作比较,以说明在TI介质中此方法分解纵横波更加准确.
图 2为背斜构造模型及对称轴倾角,其参数范围为vP(2000~3000),vS(1000~1500),ε 0.1~0.35,δ 0.05~0.18,θ -30°~30° .图 3a,b分别为正演波场的垂直分量与水平分量,在波场垂直分量中包含强的S-波能量,在波场水平分量中也含有大量P-波能量剩余;图 3c,d分别为采用Helmholtz分解方法后得到的P-波与S-波分量波场,如图所示,应用Helmholtz分解后,由于分解不彻底在各分量中保留的不同波型的剩余,这表明对TI介质不能使用各向同性介质的分解算子.图 3e,f分别为采用极化投影法分解后得到的P-波与S-波分量波场,图中可见P-波与S-波分解彻底,波型轮廓清晰,波型特征也能较好的表现,这表明由模型局部介质参数决定的高精度算子能够更精确的实现波型的分解.
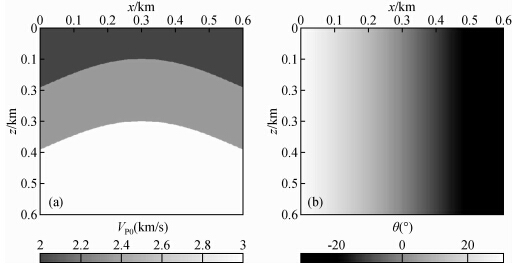 | 图 2 TI介质模型速度结构及对称轴倾角 Fig. 2 Velocity structure and tilt angle of TI medium |
 | 图 3(a)波场z分量快照,(b)波场x分量快照,(c)Helmholtz分离P-波快照,(d)Helmholtz分离后S-波快照,(e)极化投影分离后P-波快照,(f)极化投影分离后S-波快照. Fig. 3(a)Elastic wavefield z- component snapshot,(b)x- component snapshot,(c)P- wave snapshot after Helmholtz decomposition,(d)S- wave snapshot after Helmholtz decomposition,(e)P- wave snapshot after polarization projection,(f)S- wave snapshot after polarization projection. |
基于双程波动方程数值解的逆时偏移(Baysal et al., 1983)是近年来广泛受到关注的一种偏移方法,与基于射线类成像方法相比,逆时偏移可适应复杂横向速度变化,而与单程波成像方法相比,逆时偏移可对高陡倾角构造成像(张智等,2013;严红勇和刘洋,2013;张岩和吴国忱,2013;李振春等,2014).本节将纵横波分解方法应用于矢量波TI介质逆时偏移,选择一个介质模型(如图 4)生成二维多分量地震波合成资料,以此作为输入,对比分解前后波场快照(如图 5)以及最终成像结果(如图 6),考察波场延拓后纵横波分解对矢量波成像效果的影响.
 | 图 4 速度模型(a)和对称轴倾角(b) Fig. 4 Velocity model(a) and tilt angle of symmetric axis(b) |
 | 图 5 分离前后波场快照对比(a)分离前垂直分量快照;(b)分离前水平分量快照;(c)分离后P-波分量快照;(d)分离后S-波快照. Fig. 5 Comparison of wavefield snapshots between before and after decomposition(a)vertical component before decomposition;(b)horizontal component before decomposition;(c)P-wave component after decomposition;(d)S- wave component after decomposition. |
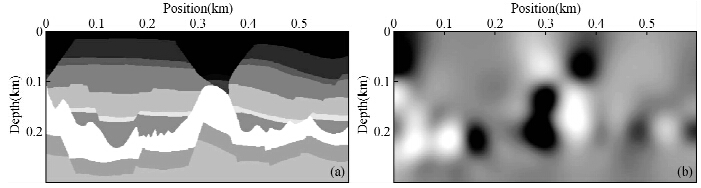
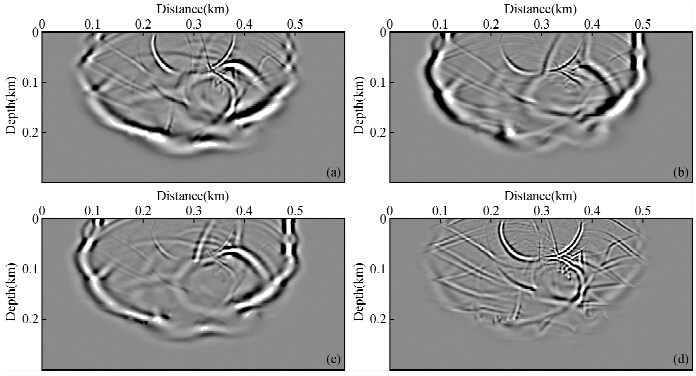
模型速度及各向异性参数范围分别为vP(1900~4500 m/s),vS(950~2250 m/s),ε(0.18~0.83),δ(0.14~0.46),θ(-30°~30°).图 5a,b分别表示延拓后矢量波场的垂直分量和水平分量快照.如图所示,垂直分量中不仅包含主要的P-波,还可看到明显的S-波剩余,同样在水平分量快照中,也有强的P-波能量,这说明在各向异性介质中矢量波场P-与SV-相互耦合,不能简单的将垂直分量与水平分量作为纵波与横波进行处理.图 5c,d表示极化投影法分离后波场分量快照,此时波场两分量中的波型分离更清晰,能够更准确的代表单一的纵波或横波波型,这表明极化投影法能够较好的分解各向异性介质中的不同波型,得到更纯的纵波与横波分量,因此避免不同波型之间的串扰,为随后的偏移处理提供更好的精度保证.图 6a,b表示直接进行矢量波逆时偏移成像结果,其中a为垂直分量结果,b为水平分量结果;图 6c,d表示基于纵横波分离的矢量波逆时偏移结果,其中c为P-P波成像结果,d为P-SV成像结果.由图中可以明显看出,基于波场分离的纯波型成像条件的矢量波偏移比一般互相关成像条件的矢量波偏移成像效果有很大的提升,在a中无法成像的构造在c中能够很好的刻画出来,同样转换波的成像效果也有较大改进,这表明基于波型分解的矢量波成像方法的有效性.此外,分离后的纯波场成像结果具有明确的物理意义,便于随后依赖于振幅的AVO或AVA等处理解释工作的进行.
 | 图 6 分离前后成像结果对比(a)分离前纵波成像;(b)分离前转换波成像;(c)分离后纵波成像;(d)分离后转换波成像. Fig. 6 Comparison of imaging results between before and after decomposition(a)P-wave imaging before decomposition;(b)P-SV imaging before decomposition;(c)P-wave imaging after decomposition;(d)P-SV imaging after decomposition. |
基于波场的矢量波场成像中,若采用初始坐标轴分量的互相关成像,会产生不同波型耦合导致的串扰噪声,并且所得成像结果不包含明确的物理意义;另一方面,在TI介质中通过计算散度和旋度无法实现纵横波的彻底分解.极化投影法能够充分考虑复杂介质的局部性质变化,模型试算表明它是一种有效的精确的纵横波分解手段.将此波型分解方法应用于各向异性介质矢量波偏移,即采用分解后纯的波型分量做互相关成像,取代原垂直分量与水平分量的直接互相关,一方面可消除部分噪音,同时得到的成像结果其物理意义精确,为之后依赖于振幅的AVO和AVA等进一步处理提供保证(秦宁等,2013;王保利等,2013).
致 谢 特别感谢李娜博士对弹性波正演方面内容的探讨;此外非常感谢编辑和审稿人的严谨态度和批评意见;最后感谢本文责编针对问题及时的沟通,谢谢你们.
| [1] | Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration[J]. Geophysics, 48(11): 1514-1524. |
| [2] | Chang W F, McMechan G A. 1994. 3-D elastic prestack, reverse-time depth migration[J]. Geophysics, 59(4): 597-609. |
| [3] | Dellinger J, Etgen J. 1990. Wave-field separation in two-dimensional anisotropic media[J]. Geophysics, 55(7): 914-919. |
| [4] | Hokstad K. 2000. Multicomponent Kirchhoff migration[J]. Geophysics, 65(3): 861-873. |
| [5] | Kuo J T, Dai T F. 1984. Kirchhoff elastic wave migration for the case of noncoincident source and receiver[J]. Geophysics, 49(8): 1223-1238. |
| [6] | Moczo P, Robertsson J O A, Eisner L. 2007. The finite-difference time-domain method for modeling of seismic wave propagation[J]. Advances in Geophysics, 48(6): 421-516. |
| [7] | Sun R, McMechan G A. 2001. Scalar reverse-time depth migration of prestack elastic seismic data[J]. Geophysics, 66(5): 1519-1527. |
| [8] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Geophysics, 51(4): 889-901. |
| [9] | Yan J, Sava P. 2008. Isotropic angle-domain elastic reverse-time migration[J]. Geophysics, 73(6): S229-S239. |
| [10] | Yan J, Sava P. 2011. Elastic wave-mode separation for TTI media[J]. Geophysics, 76(4): T65-T78. |
| [11] | Zhang Y, Zhang H Z, Zhang G Q. 2011. A stable TTI reverse time migration and its implementation[J]. Geophysics, 76(3): WA3-WA11. |
| [12] | 底青云, 王妙月. 1997. 弹性波有限元逆时偏移技术研究[J]. 地球物理学报, 40(4): 570-579. |
| [13] | 董良国, 马在田, 曹景忠. 2000. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 43(6): 856-864. |
| [14] | 杜启振, 秦童. 2009. 横向各向同性介质弹性波多分量叠前逆时偏移[J]. 地球物理学报, 52(3): 801-807. |
| [15] | 冯晅, 张先武, 刘财,等. 2011. 带有多道相关的抛物线Radon变换法分离P-P、P-SV波[J]. 地球物理学报, 54(2): 304-309. |
| [16] | 何兵寿, 张会星. 2006. 多分量波场的矢量法叠前深度偏移技术[J]. 石油地球物理勘探, 41(4): 369-374. |
| [17] | 胡天跃, 张广娟, 赵伟,等. 2004. 多分量地震波波场分解研究[J]. 地球物理学报, 47(3): 504-508. |
| [18] | 李博, 李敏, 刘红伟,等. 2012. TTI介质有限差分逆时偏移的稳定性探讨[J]. 地球物理学报, 55(4): 1366-1375. |
| [19] | 李振春, 郭振波, 田坤. 2014. 黏声介质最小平方逆时偏移[J]. 地球物理学报, 57(1): 214-228. |
| [20] | 李志远, 梁光河, 谷丙洛. 2013. 基于散度和旋度纵横波分离方法的改进[J]. 地球物理学报, 56(6): 2012-2022. |
| [21] | 秦宁, 李振春, 张凯,等. 2013. 弹性矢量波成像域联合层析反演[J]. 地球物理学报, 56(9): 3109-3117. |
| [22] | 王保利, 高静怀, 陈文超,等. 2013. 逆时偏移中用Poynting矢量高效地提取角道集[J]. 地球物理学报, 56(1): 262-268. |
| [23] | 王娟, 李振春, 陶丽. 2012. 逆时偏移成像条件研究[J]. 地球物理学进展, 27(3): 1173-1182. |
| [24] | 夏凡, 董良国, 马在田. 2004. 三维弹性波数值模拟中的吸收边界条件[J]. 地球物理学报, 47(1): 132-136. |
| [25] | 谢飞, 常旭, 刘伊克. 2008. 火山岩地震屏蔽层的转换波叠前时间偏移成像[J]. 地球物理学报, 51(6): 1899-1908. |
| [26] | 严红勇, 刘洋. 2013. 基于时空域自适应高阶有限差分的声波叠前逆时偏移[J]. 地球物理学报, 56(3): 971-984. |
| [27] | 张美根, 王妙月. 2001. 各向异性弹性波有限元叠前逆时偏移[J]. 地球物理学报, 44(5): 711-719. |
| [28] | 张岩, 吴国忱. 2013. TTI介质qP波逆时偏移中伪横波噪声压制方法[J]. 地球物理学报, 56(6): 2065-2076. |
| [29] | 张永刚, 王赟, 王妙月. 2004. 目前多分量地震勘探中的几个关键问题[J]. 地球物理学报, 47(1): 151-155. |
| [30] | 张智, 刘有山, 徐涛,等. 2013. 弹性波逆时偏移中的稳定激发振幅成像条件[J]. 地球物理学报, 56(10): 3523-3533. |
 2014, Vol. 29
2014, Vol. 29

