2. 中国石化西南油气分公司勘探开发研究院, 成都 618000
2. Exploration & Production Research Institute, SWPB., SINOPEC, Chengdu 618000, China
由于转换波技术在气云成像、流体识别和裂缝检测等方面具有优势(马昭军和唐建明,2007),近几年成为一个研究热点.转换波Kirchhoff叠前偏移技术是转换波地震数据处理中的一项核心技术(Liu et al., 2009),但是由于偏移假频的存在,会严重降低转换波偏移成像的质量和精度.转换波Kirchhoff偏移方法主要涉及到三种假频(Zhang,2009),因采样不足导致的数据假频,因偏移计算方法不当造成的算子假频,以及偏移输出网格选取不当产生的成像假频.其中,和偏移算法本身紧密联系的是上述所提出的算子假频,因此如何去除算子假频提高偏移成像质量是转换波Kirchhoff叠前时间偏移中的重要研究内容.
关于转换波偏移中反算子假频的方法目前国内外涉及的文献很少,只有一些资料提及了关于纵波的反算子假频的基础理论(David et al., 2001;石颖等,2013),如何推导出常规纵波的反假频公式,如何构建常规纵波的反假频滤波器(Cary,1997;Abma et al., 2001),以及算子假频在实际地震资料处理中的对成像影响分析等方面(Robein,2012),但几乎没有关于如何在转换波Kirchhoff偏移中实现反算子假频的,也没有文献提及如何利用GPU高性能计算方法实现反算子假频算法(刘国峰等, 2009a,2009b,2009c;李晶等,2011;张锦涛等,2013;刘守伟等,2013).
对输入数据先进行反算子假频滤波后偏移求和等价于对输入数据进行插值再偏移求和,文章以这一结论为切入点,通过转换波Kirchhoff叠前时间偏移理论公式和常规纵波反假频理论公式进行对比引申,推导出转换波三维偏移反假频的理论公式,从而避免了转换波反假频的复杂公式推导和转换波参数,利用奈奎斯特采样定理和基于Z变换的复数滤波器设计方法构建了局部三角形滤波器(Biondo,2005),新颖的将反假频结合GPU高性能计算技术,实现了基于CUDA的并行三角局部滤波,能大幅提高反假频计算效率,通过川西区块的地震资料进行测试,对测试结果进行分析,基于CUDA的转换波Kirchhoff偏移反假频算法能有效快速的去除偏移中存在的算子假频.1 转换波Kirchhoff偏移反假频理论 1.1 转换波Kirchhoff叠前时间偏移原理
算子假频是由于偏移计算方法本身造成的,因此实现反算子假频要从转换波Kirchhoff叠前时间偏移的原理入手.转换波Kirchhoff叠前时间叠前偏移是假设地下每个点都是一个绕射点,通过计算炮点到成像点下行P波旅行时tS和tP成像点到检波器上行S波的旅行时,将PS波双程旅行时tPS的上能量进行克希霍夫叠加,将能量叠加到成像点处,这样就完成了一个绕射点的“聚焦”.(Dai et al., 2004)在二维时间偏移过程中,克希霍夫叠加算子轨迹表现为一个椭圆,而在三维时间偏移中,克希霍夫叠加算子轨迹表现为一个椭球面.在转换波时间偏移过程中采用的是均方根速度场,可以逐点进行速度分析,较叠后偏移的方法,成像精度较高,偏移速度较快,对速度模型精度的要求较低,适合于横向速度变化不大地区进行地震资料处理.转换波Kirchhoff叠前时间偏移成像示意图如图 1所示:
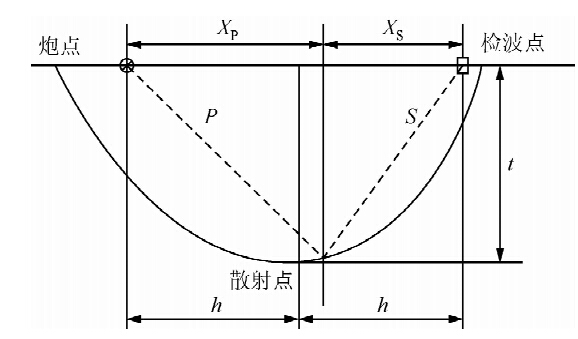 | 图 1 转换波成像示意图 Fig. 1 C-wave PSTM schematic diagram |
因为直接讨论转换波的反假频会涉及到更复杂的转换波反假频公式和转换波参数,所以在研究这个问题的时候,从纵波的反假频分析开始,结合转换波偏移公式进行的推导引申,从而避免将问题变得复杂化.在实际偏移过程中地震道要进行克希霍夫叠加,而相邻道存在道间距,不是足够稠密的,因而偏移算子的剩余时差就不能满足奈奎斯特采样定理,从而产生了偏移算子假频,其产生的本质还是因为数据不满足奈奎斯特采样定理,降低偏移成像质量,因此需要在时空域进行反算子假频处理.
算子假频是因为采样率不足造成的,自然可以通过插值的方法进行输入数据重建,再进行转换波偏移,从而达到满足奈奎斯特采样定理的条件,但是这样一来输入数据和偏移工作量就会成倍增加,所以不得不选择其它替代方法.对输入的转换波数据进行反算子假频的滤波处理,然后再进行偏移处理也同样可以满足采样定理的条件,并且输入数据量不会增加.由此得到结论,对输入数据先进行算子假频滤波后偏移求和等价于对输入数据进行插值再偏移求和.
因为对输入数据先进行算子假频滤波后偏移求和等价于对输入数据进行插值再偏移求和,为避免插值带来的计算量指数级的增加,利用反假频滤波就可以引出反算子假频的基本公式(Lumley et al., 2001)为
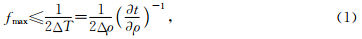
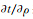 表示偏移算子与地震道交点处的局部空间导数项,Δρ是记录的是地表地震道间距.从该式可以得出,要抑制算子假频可以通过对地震道进行局部低通滤波来实现.
表示偏移算子与地震道交点处的局部空间导数项,Δρ是记录的是地表地震道间距.从该式可以得出,要抑制算子假频可以通过对地震道进行局部低通滤波来实现. 对于纵波,由于ρ是一个距离矢量,根据距离公式,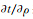 可以沿x轴和y轴方向进行分解:
可以沿x轴和y轴方向进行分解:


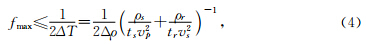
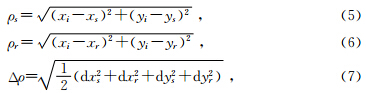
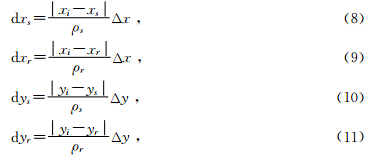
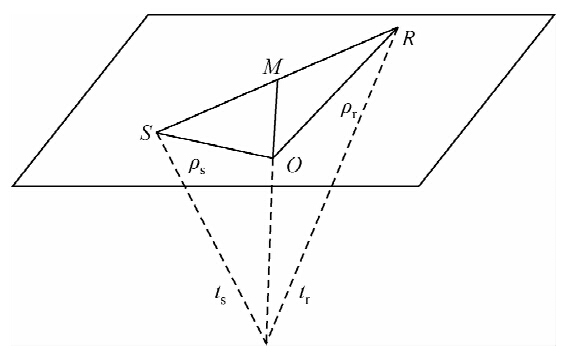 | 图 2 转换波偏移几何关系图 Fig. 2 C-wave PSTM diagram of geometric relationships |
文章上述已经将反假频问题转换成一个低通滤波的问题,已知转换波偏移算子做克希霍夫画弧不产生假频所需要的最大频率fmax,就需要设计一种方法来实现地震数据的局部低通滤波,参照纵波反假频的方法(Kristiansen et al., 2003),选取了三角形滤波器来构建局部低通滤波,由于N点的数字三角形滤波器的Z变换表达式为
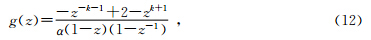
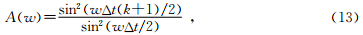
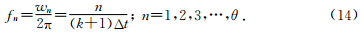
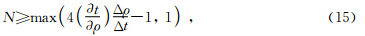
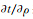 可由公式(3)得出.在实际算法实现过程中,可以注意到N点的数字三角形滤波器的Z变换表达式实际是一个复数滤波器,而地震数据是一个实数序列,因此可以对三角形滤波器Z变换公式进行进一步化简,退化为一个实数滤波器再进行滤波处理.
2.2 基于CUDA转换波反假频算法实现
可由公式(3)得出.在实际算法实现过程中,可以注意到N点的数字三角形滤波器的Z变换表达式实际是一个复数滤波器,而地震数据是一个实数序列,因此可以对三角形滤波器Z变换公式进行进一步化简,退化为一个实数滤波器再进行滤波处理.
2.2 基于CUDA转换波反假频算法实现由于计算转换波反算子假频算法本身就比较复杂,对于每一个偏移算子都要进行反复大量的计算,因此计算速度非常慢,而反假频算子之间的计算逻辑上是相互独立,而原有的转换波Kirchhoff叠前时间偏移算法已经利用CUDA实现(喻勤等,2013),因此根据这两个特点引入了基于CUDA的GPU高性能计算能力实现反假频算法,这是文章另一个创新之处,将高性能计算技术和反假频算法结合起来高效的实现偏移反假频.
因为反假频算法基本思路是采取先对偏移输入数据进行算子假频滤波后再进行偏移求和的方法.从算法实现的角度看,反假频算法和转换波叠前时间偏移的核心算法在逻辑上是隔绝开的,反假频算法只跟输入数据相关,因此实现过程中将反假频算法加入到原有偏移数据读取到GPU显存上这个步骤之后.
由于在进行反算子假频处理中,需要先求取反假频滤波器长度,而计算滤波器长度又需要计算偏移核心算法里面的一些参数,因此算法上要求和偏移核心算法对数据分配方式保持相同,且在计算同一块数据时反假频算法和偏移核心算法是有先后顺序的.在获取必要的计算参数后,就可以根据公式(15)求取数字三角形滤波器长度N.在求取了滤波器长度N以后,就可以根据N构建一个低通数字滤波器,对偏移输入数据进行低通滤波处理.
在具体的基于CUDA的反假频算法实现过程中主要关键点在于:
(1)由于原有的基于CUDA的偏移核心算法中,在数据分组上是按照CUDA中的一个block处理一道,每个thread对应时间轴上的一点来进行划分的,因为偏移中的block和thread的选取是根据硬件的计算资源进行确定的,而数据分配方式要保持相同,因此在反假频算法中,block和thread划分方式仍是按照偏移设计的方式分配.
(2)在计算同一块数据时反假频算法和偏移核心算法是有先后顺序的,因此在GPU并行算法实现时要确保两个计算模块的顺序,要求是同步完成的,实现过程中采用了CUDA中的处理流媒体数据经常用到的stream方式(Nvidia,2013),由于该方式可以确保一个stream中计算是有先后顺序的,这样一来就能确保一块数据先进行反假频处理再进行偏移处理,而且stream之间是异步执行的,这样所有的处于不同块的数据可以异步同时进行计算,可以提高计算效率.
(3)在计算滤波器长度时,由于长度时动态变化的,计算量很大,这里需要在GPU上坐一些优化.因为从之前的matlab仿真算法中得到了一些先验的结论,滤波器长度在浅层变化明显,而之后就变化缓慢,在比较大时间点之后,假频几乎没有对数据造成影响.利用上述先验结论,在实现时采取了动态的时窗滤波,在浅层的时窗比较小,随着地层深入时窗取值也变化较大,在一个时窗计算的点计算一个均值代替这个时窗滤波器长度的取值.在CUDA上并行计算多个数据时窗存入texture memory(ohn,2008)中,这样在寻址时可以提高速度.
(4)对于滤波计算的CUDA实现,由于在时域上是卷积计算,在GPU上实现快速计算的难度比较大,所以需要将数据变换到频域上,这样就可以变成频域相乘,就利用了CUDA的cuFFT(张舒等,2009)快速傅里叶变换库将输入数据变换到频域上,在频域上采用GPU比较经典并行相乘加和(Nickolls et al., 2007)的方式得到滤波后的频域数据,最后再次利用cuFFT进行反变换得到时域数据.利用GPU的并行能力将输出数据拼成一个完整的反假频滤波后数据.
在得到经过反假频处理的数据后,就可以进行基于CUDA的叠前时间偏移核心算法的并行计算,整个反假频偏移计算的具体算法流程图如图 3所示.
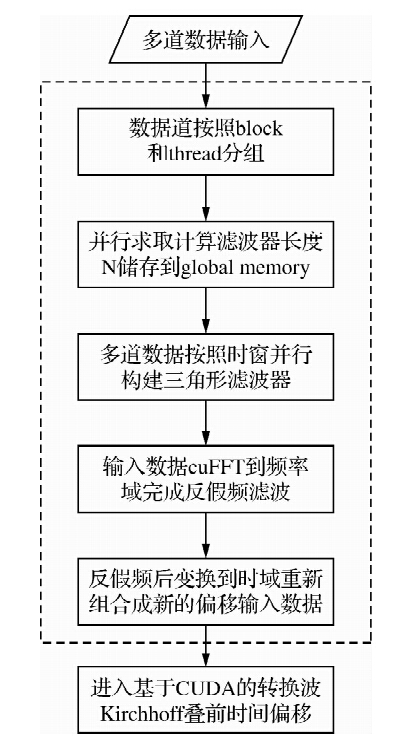 | 图 3 基于CUDA的转换波反假频算法流程图 Fig. 3 C-wave PSTM Anti-aliasing algorithm flow chart |
为测试基于CUDA的转换波Kirchhoff叠前时间偏移反假频并行算法的性能,在Linux操作系统下构建了算法模块,实现了该算法.测试平台采取了Intel Xeon(R)CPUX5570 @ 2.93 GHz的处理器,24GBDDR3 1066 MHz的内存,测试平台配置了一块Quadro FX 5800显卡,PCI-Express 2.0 x16的图形卡接口,软件工具采取eclipse 3.8、toolchain以及cuda5.0的编译器.
先对算法利用构造的理论点脉冲数据进行了测试,在接收道构造了一个脉冲,分别利用反假频和未反假频的转换波Kirchhoff叠前时间偏移算法进行了偏移,偏移的结果如图 4所示.
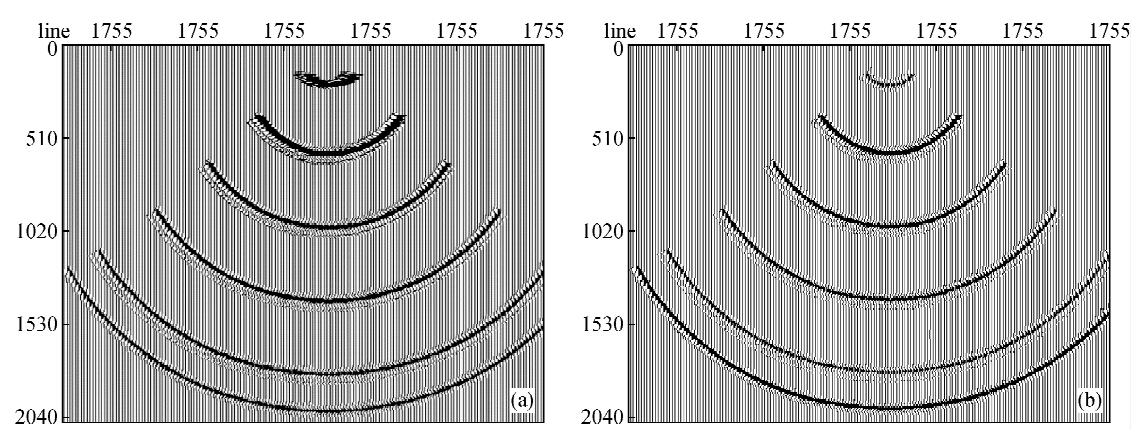 | 图 4 未反假频处理(a)和反假频处理后(b) Fig. 4 Without Anti-aliasing(a) and Anti-aliasing(b) |
实际转换波数据测试选取川西某区块一块数据来进行偏移成像,数据量为19.6 G,使用未进行反假频处理和反假频处理两种方式进行偏移成像结果如图 5所示:
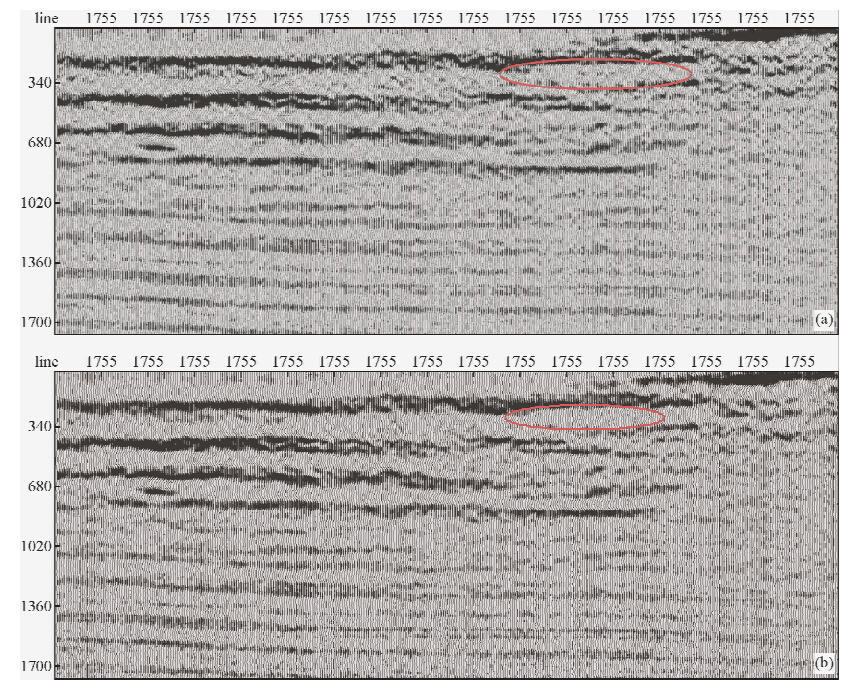 | 图 5 反假频处理前(a)和反假频处理后(b) Fig. 5 Without Anti-aliasing(a) and Anti-aliasing(b) |
从以上测试可以看出,在利用理论构点脉冲数据进行测试时,在未反假频的情况下,浅层的弧由于假频的存在产生的噪声湮没了有效数据,经过假频处理后浅层的偏移画弧变得清晰了.对于川西某区块的利用未进行偏移处理和进行偏移处理的结果可以看到,虽然所处理的工区构造比较平坦,假频现象并不严重,但仍可以看到在未经假频处理的偏移剖面上可以看到浅层的层间有假轴和假的断块出现,而经过假频处理后,假轴消失了,这也表明了假频存在所带来的影响,通过反假频算法可以将假频去除,从而因假频存在产生的影响也随之消失.
对偏移反假频算法进行性能分析,为得到CPU与GPU程序运行的加速比,利用一个大小为19.6 G的实际地震数据进行测试,以运行的平均值为最后的运算时间,作为性能分析的依据.先仅就反假频算法本身测试,反假频部分利用CPU和GPU分别实现,对于19.6 G的数据在CPU上实现反假频,总计算时间为401623 ms,在GPU上实现反假频总计算时间为11484325 ms,程序加速比达到28.59倍.然后利用整个转换波Kirchhoff叠前时间偏移算法是在GPU上实现的,加上利用CPU和GPU实现的反假频算法部分,对于19.6G的数据在CPU上实现反假频,在GPU上进行偏移总计算时间为19095759 ms,反假频和偏移全部在GPU上进行计算,总计算时间为8011567 ms,程序加速比达到2.38倍,测试结果如表 1所示.
|
|
表 1 CPU和GPU程序测试运行时间 Table 1 CPU and GPUrun time test |
从得到的加速比结果来看,基于CUDA的反假频并行算法,程序在原有基础上得到单卡接近30倍的性能提升,引入反假频算法的转换波Kirchhoff叠前时间偏移算法整体性能也得到了2倍多的提升.
此处加速比的含义:
加速比=CPU实现执行时间/GPU并行执行时间. 5 结 语
文章的创新之处在于通过对常规纵波反假频公式进行引申推导出转换波的反假频公式,利用三角形数字滤波器实现了反假频算法,结合CUDA高性能计算技术实现了Kirchhoff叠前时间偏移反假频并行算法.文章最后对算法进行了测试分析,结果表明GPU反假频并行算法能有效的去除算子假频,计算效率得到很大的提高,对于偏移反算子假频问题需要进一步考虑的是,由三角形滤波器构建的滤波在反假频算法中是否就是最优的,利用GPU高性能能力能够快速的构建高斯滤波器,是否会取得更好效果也是一个值得研究的问题,反假频滤波器选取的准则究竟是什么也值得做进一步的研究.
致 谢 文章所作研究受到了中石化多波地震技术重点实验室的支持和国家重大专项国家科技重大专项课题《四川盆地碎屑岩层系大中型油气田形成规律与勘探方向(二期)》下属专题《多波地震资料处理软件关键模块研发》的资助,特此感谢.| [1] | Abma R, Sun J,Bernitsas N.2001.Antialiased methods in Kirchhoffmigration[J].Geophysics,64(6):1783-1792. |
| [2] | Bevc D, Lumley D E.2001. When is anti-aliasing needed in Kirchhoff migration [R]. Stanford Exploration Project, Report 80, 1-9. |
| [3] | Biondo B L.2005.Kirchhoff imaging beyond aliasing [R].Stanford Exploration Project, Report, March1,1-45. |
| [4] | Cary P. 1997.Migration Operator Aliasing and its Effect on Interpolation[J].CSEG Recorder, 28(2):166-176. |
| [5] | DaiH C,Li X Y, Conway P. 2004. 3D Pre-stack kichhoff time migration of PS-waves and migration velocity model building[C].//74th Ann.Internat.Mtg.:Soc.Expl. Geophysics,1115-1118. |
| [6] | Fan W H,Yang C C,Sun C W, et al. 2007. Application of prestack time migration forthree dimensional seismic data[J]. Progress in Geophys.(in Chinese),22(3):836-842. |
| [7] | Kristiansen P, Fowler P, Mobley E. 2003. Anisotropic Kirchhoff prestack time migrationfor enhancedmulticomponent imaging[C].//73rd Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 961-964. |
| [8] | Li J, Wang C X,Li J L, et al.2013. The recent overseas development of pre-stack migration of seismic data[J]. Progressin Geophys.(in Chinese),26(3):966-982.doi:10.3969/j.issn.1004-2903.2011.03.024. |
| [9] | Li X Y,Dai H C, Mancini F. 2007. Converted-wave imaging in anisotropic media:Theory and case studies[J].Geophysical Prospecting, 55(3): 345-363. |
| [10] | Liu G F, Liu H, Wang X M, et al. 2009. Two kinds of traveling time computation and parallelcomputing methods of Kirchhoff migration[J].Progress in Geophys.(in Chinese),24(1):131-136. |
| [11] | Liu G F, Liu H, Li B, et al. 2009. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation[J]. Chinese J. Geophys.(in Chinese), 52(12):3101-3108. |
| [12] | Liu G F, Liu Q, Li B, et al. 2009. GPU/CPU co—processing parallel computation for seismic data processing in oil and gasexploration[J]. Progress in Geophys(in Chinese), 24(5):1671-1679. |
| [13] | Liu S W, Wang H Z, Chen S C, et al. 2013.Implementation strategy of 3D reverse time migration on GPU/CPU clusters[J]. Chinese J. Geophys.(in Chinese), 56(10):3487-3496.doi:10.6038/cjg20131023. |
| [14] | Lumley D E, Claerbout J F, Bevc D. 2001a. Anti-aliased Kirchhoff 3-D migration[J].Geophysics,32(4):1282-1285. |
| [15] | Lumley D E,Claerbout J F,Bevc D. 2001b. Anti-aliased Kirchhoff 3-D migration[R]. Stanford Exploration Project, Report 80, 1-444. |
| [16] | Ma Z J,Tang J M. 2007. The application of prestack time migration in 3D converted-wave data processing[J]. Geophysical Prospecting for Petroleum,46(2):174-180. |
| [17] | Nvidia. 2013. Nvidia CUDA Compute Unified Device Architecture programming guide version5.1[EB/OL].http:developer.download.Nvidia.com/compute/cuda/ 5_0/docs/CudaReference Manual_5.0.pdf. |
| [18] | Nickolls J. 2007. Nvidia GPU parallel computing architecture[J]. IEEE Hot Chips, 19(2):151-160. |
| [19] | Owens J D, Houston M, Luebke D, et al. 2008. GPUcomputing[J].Proceedings of the IEEE, 96(5):879-899. |
| [20] | Robein E. 2012. Seismic Imaging: A Review of the Techniques, their Principles, Merits and Limitations[M].Beijing: PetrologyPublishing Press,30-35. |
| [21] | Shi Y, Zhang Z, Wang J M, et al. Investigation on anti-aliasing regularization approach for seismic data[J]. Progressin Geophys.(in Chinese), 2011, 28(1):250-256.doi:10.6038/pg20130126. |
| [22] | Yu Q,Chen B J, Kong X L. 2013. Implemnet converted-wave Kirchhoff prestack time migration base on CUDA [J]. Oil Geophysical Prospecting,48(1):58-63. |
| [23] | Zhang J T, Zhao J T,Wang Z L. 2013. Analysis of GPU and FPGA parallel computing--example of Kirchhoff prestack time migration [J]. Progress in Geophys.(in Chinese), 28(3):1464-1471.doi:10.6038/pg20130341. |
| [24] | Zhang S,Chu Y L,Zhao K Y, et al. 2009. GPU High Performance Computing on CUDA[M]. Beijing: China Publishing Company of Water Conservancy and Electric Power. |
| [25] | Zhang Y. 2009. The migration aliasing problems and imaging resolution analysis[R].CGGVeritas Annual Research Report, 210. |
| [26] | 樊卫花,杨长春,孙传文,等.2007.三维地震资料叠前时间偏移应用研究[J].地球物理学进展, 22(3):836-842. |
| [27] | 李晶,王成祥,李军茹,等. 2011. 地震资料叠前偏移成像技术进展[J].地球物理学进展,26(3):966-982.doi:10.3969/j.issn.1004-2903.2011.03.024. |
| [28] | 刘国峰,刘洪, 王秀闽,等. 2009a. Kirchhoff积分叠前时间偏移的两种走时计算及并行算法[J].地球物理学进展,24(1):131-136. |
| [29] | 刘国峰,刘洪,李博,等. 2009b. 山地地震资料叠前时间偏移方法及其GPU实现[J].地球物理学报,52(12):3101-3108. |
| [30] | 刘国峰,刘钦,李博,等. 2009c. 油气勘探地震资料处理GPU/CPU协同并行计算[J].地球物理学进展,24(5):1671-1679. |
| [31] | 刘守伟 ,王华忠,陈生昌,等. 2013. 三维逆时偏移GPU/CPU机群实现方案研究[J].地球物理学报, 56(10):3487-3496.doi:10.6038/cjg20131023. |
| [32] | 马昭军,唐建明. 2007. 叠前时间偏移在三维转换波资料处理中的应用[J]. 石油物探,46(2):174-180. |
| [33] | Robein E.2012. 地震资料叠前偏移成像——方法、原理和优缺点分析[M]. 北京: 石油工业出版社: 30-35. |
| [34] | 石颖,张振,王健民,等. 2013. 地震数据反假频规则化方法研究[J].地球物理学进展,28(1):250-256.doi:10.6038/pg20130126. |
| [35] | 喻勤,程冰洁,孔选林. 2013. 基于CUDA的转换波Kirchhoff叠前时间偏移算法研究及实现[J]. 石油地球物理勘探,48(1):58-63. |
| [36] | 张锦涛,赵惊涛,王真理. 2013. FPGA与GPU并行计算分析——以Kirchhoff叠前时间偏移为例[J].地球物理学进展,28(3):1464-1471.doi:10.6038/pg20130341. |
| [37] | 张舒,褚艳丽,赵开勇,等. 2009. GPU高性能运算之CUDA[M].北京: 中国水利电力出版社. |
 2014, Vol. 29
2014, Vol. 29

