2014, Vol. 29
2. 中国国土资源航空物探遥感中心, 北京 100083
2. China Aero Geophysical Surrey & Remote Sensing Center for Land and Resources, Beijing 100083, China
由于常规的位场处理、转换和定性解释大多基于平面数据，然而实际的位场观测面大多是曲面甚至是间断面，因此研究曲面上的位场处理和转换方法不仅具有一定的理论意义，更具有重要的现实意义.自20世纪60年代开始，地球物理学家们提出了一些曲面位场处理和转换方法，并进行了各种改进和完善.如等效源法、单层位法、偶层位法、有限项调和级数法、三角函数法、球谐级数法、泰勒级数法等(Dampney，1969；Handerson and Cordell，1971；Emilia，1973；Battacharyya and Chen，1977；Nakatsuka，1981；杜维本，1982；陈钟琦，1983；Hansen and Miyazaki，1984；侯重初等，1985;侯重初和管志宁，1995；管志宁等，1985；徐连喜，1988；梁锦文，1988；杨再朝，1989；Pilkington and Urquhartt，1990；夏江海，1991，1993；王万银和潘作枢，1996，1997；姚长利等，1997；徐世浙等，2002；刘金兰等，2007；于长春等，2007;王万银等，2009).
偶层位法是曲面位场处理和转换方法中使用效果较好的一种方法，分空间域和频率域两种.1990年Pilkington等人将频率域快速Fourier变换技术与空间域偶层位法相结合，提出了频率域偶层位法，并在曲面位场处理和转换中取得了良好的效果.之后，Xia等(1991，1993)和王万银等(2009)分别研究了频率域偶层位法，对该方法的技术措施进行了详细研究，并通过理论模型和实际资料检验了方法的有效性(于长春等，2007；王万银等，2009).
本文就频率域偶层位法的适应性、计算精度及稳定性进行研究.从场源分布和观测面起伏两个方面研究频率域偶层位法的适应性及计算精度；从不同大小随机干扰测试其稳定性.有关频率域偶层位法的基本原理及偶层面位置的布置试验请参考有关文献(王万银等，2009). 1 基本模型设计及误差评价方式 1.1 基本模型设计
为便于进行模型试验对比，设置了三种基本模型.这三种基本模型由四个场源体(直立六面体)和两种观测面组成.四个场源体为直立六面体(编号为1、2、3和4)，其几何参数及磁性参数见表 1所示.第一种观测面取自Bhattacharyya和Chen(1977)所用的观测面；观测面的z坐标方向向下为正，最高测点值为-5.3 km，最低测点值为1.7 km，高差为7.0 km；观测面以0.5 km为间距分成105×105个网格点，其起点和起线坐标都是-26.0 km，终点和终线坐标都是26.0 km；图幅向右为x坐标正方向，图幅向上为y坐标正方向，图幅中心为坐标原点.第二种观测面是截取了第一种观测面左上角的部分(x：-26.0 km -2.0 km、y：-2.0 km -26.0 km)，按照比例将其平面坐标单位换算为x：-26.0 km -26.0 km、y：-26.0 km -26.0 km，之后对数据以0.5 km为间距进行网格化而形成的105×105个网格点；其最高测点z坐标为-5.3 km，最低测点z坐标为-0.5 km，高差为4.8 km.
 | 表 1 直立六面体场源参数统计表 Table 1 Parameters table of vertical hexahedral field source |
第一个基本模型场源为1号单一直立六面体，观测面为第二种观测面；第二个基本模型场源为1号单一直立六面体，观测面为第一种观测面；第三个基本模型场源为2号、3号和4号三个直立六面体组合，观测面为第一种观测面(Bhattacharyya所用模型).三种基本模型的观测面起伏和场源体平面位置见图 1所示(图中白色矩形方框表示直立六面体的平面位置)，在观测面上地磁倾角为50°、偏角为50°的理论磁力异常ΔT、化极磁力异常及其垂向一阶导数分别见图 2、图 3和图 4所示.
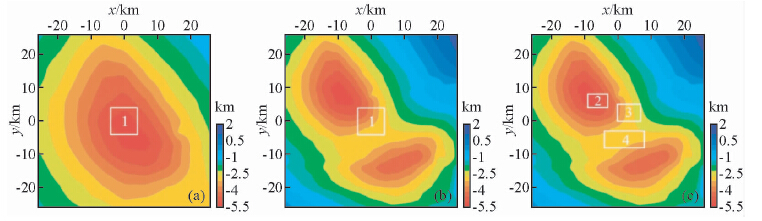 | 图 1 观测面起伏及直立六面体平面位置图
(a)基本模型一；(b)基本模型二；(c)基本模型三.图中白色方框表示直立六面体的平面位置. Fig. 1 The plane position of magnetic bodies and the rolling topography(a)Basic model one;(b)Basic model two;(c)Basic model three. The white solid lines represent the edge location of the models. |
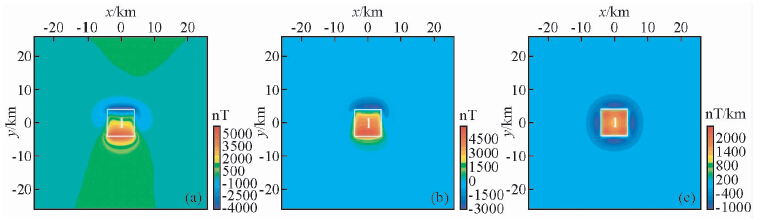 | 图 2 基本模型一在观测面上的磁异常图
(a)磁力异常ΔT(nT);(b)化极磁力异常(nT);(c)化极磁力异常垂向一阶导数(nT/km). Fig. 2 The magnetic anomaly map of basic model one on the observation surface(a)Magnetic anomaly ΔT(nT);(b)RTP(nT);(c)RTP-VDR(nT/km). |
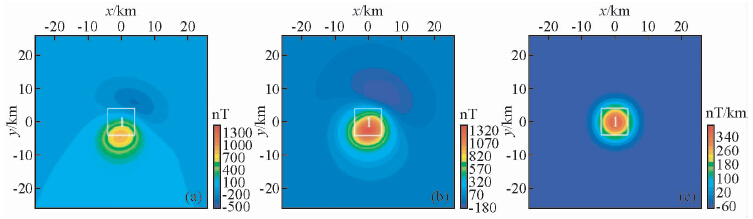 | 图 3 基本模型二在观测面上的磁异常图
(a)磁力异常ΔT(nT)；(b)化极磁力异常(nT)；(c)化极磁力异常垂向一阶导数(nT/km). Fig. 3 The magnetic anomaly map of basic model two on the observation surface(a)Magnetic anomaly ΔT(nT)；(b)RTP(nT)；(c)RTP-VDR(nT/km). |
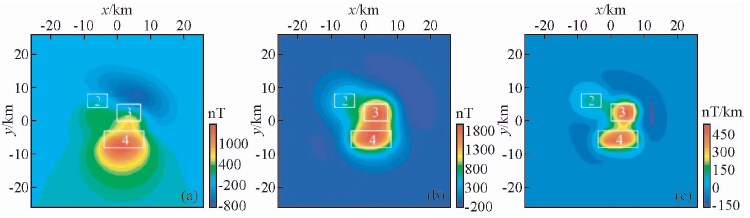 | 图 4 基本模型三在观测面上的磁异常图
(a)磁力异常ΔT(nT)；(b)化极磁力异常(nT)；(c)化极磁力异常垂向一阶导数(nT/km). Fig. 4 The magnetic anomaly map of basic model three on the observation surface(a)Magnetic anomaly ΔT(nT)；(b)RTP(nT)；(c)RTP-VDR(nT/km). |
为了统计频率域偶层位法曲面处理和转换结果的精度，对模型测试结果要进行误差统计.假设某点的理论值为Ai、计算值为Bi，共有m个点，则通常使用均方误差
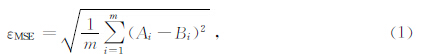
由于位场数据存在正常背景场的影响，为了消除这一背景场对误差统计结果的影响，采用均值均方误差
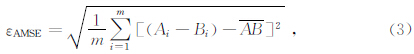
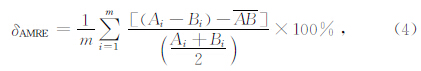
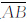表示残差(Ai－Bi)(i=1，2，…，m)的平均值，可表示为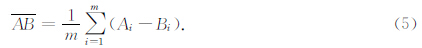
由于相对误差不适应量值较小的数据体误差统计，均方误差不适应量值较大的数据体误差统计.故对均值均方误差除以幅值(Amax－Amin)得到归一化均值均方误差εNAMSE
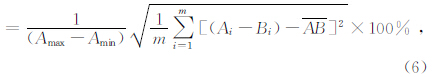
因此，对模型测试结果进行误差统计时采用均值均方误差εAMSE来衡量计算结果的误差大小，用归一化均值均方误差εNAMSE来代替均值平均相对误差评价计算结果的误差变化规律.另外，在模型测试过程中不再把向上延拓和向下延拓分开进行误差统计，而是一起参与误差统计. 2 场源分布影响试验
场源分布指场源的不同组合及与观测面的相对位置变化.首先利用基本模型一中单一直立六面体不同埋深来测试频率域偶层位法能否适应“强地形”的情况；采用基本模型二中单一直立六面体不同埋深和不同水平尺寸来测试频率域偶层位法受场源埋深和规模大小的影响程度；采用基本模型三来测试频率域偶层位法受场源组合的影响程度. 2.1 “强地形”影响试验
从理论上来讲，频率域偶层位法不能适应于“强地形”，但到底能不能适应于“强地形”的情况则需要进行模型测试.在基本模型一上移动直立六面体场源体的垂向位置，将其顶面z坐标分别移动到-4.0 km、-3.0 km、-2.0 km、-1.0 km、0.0 km、1.0 km、2.0 km和3.0 km，当场源体顶面z坐标分别为-4.0 km、-3.0 km、-2.0 km和-1.0 km时，属于“强地形”情况.场源体顶面z坐标等于-4.0 km时为完全“强地形”，其所有场源位于最低测点以上；场源体顶面z坐标为-1.0 km时为最弱“强地形”，其所有场源基本位于最低测点以下.场源体顶面z坐标为0.0 km、1.0 km、2.0 km和3.0 km时为“弱地形”情况，场源体顶面z坐标为0.0 km时为最强“弱地形”.
运用频率域偶层位法对上述8种场源位置进行了曲面处理和转换试验，分别计算了最高测点以上观测平面(z=-6.0 km)的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数.对计算结果进行了均值均方误差和归一化均值均方误差统计(图 5)，由图 5可以看出，随着场源体顶面距观测面的距离越来越小(直立六面体顶面z坐标值越小)，计算得到的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数的误差越来越大，一般呈二次型增大；当场源体顶面z坐标为-4.0 km时，场源体全部位于最低测点以上，虽然从计算结果来看比较稳定，但误差却相对较大；随着场源体埋深的增加，误差逐渐减少；当场源体顶面z坐标为-1.0 km时，场源体基本全部位于最低测点以下，其误差与“弱地形”(场源体z坐标为0.0 km、1.0 km和2.0 km)的误差大小基本接近.
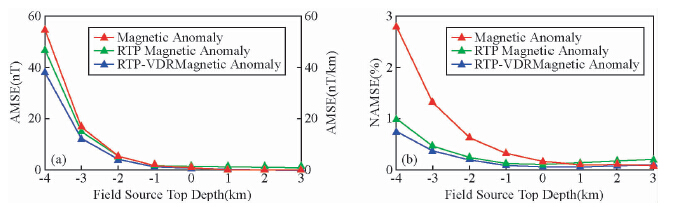 | 图 5 不同埋深场源在z=-6.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差;(b)归一化均值均方误差. Fig. 5 The processing and transforming results error map on z=-6.0 km plane by different field source top depths model(a)Average mean square error;(b)Normalized average mean square error. |
为了试验场源埋藏深度对频率域偶层位法的影响，选用基本模型二，并设置场源体顶面z坐标分别为3.0 km(同基本模型二)、3.5 km、4.0 km、4.5 km、5.0 km、5.5 km、6.0 km、6.5 km和7.0 km进行试验.计算了z=-2.0 km平面(观测面平均平面)上的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数，并进行了均值均方误差和归一化均值均方误差统计(图 6).从误差统计结果来看，当场源体埋藏深度增大时，磁力异常、化极磁力异常和化极磁力异常垂向一阶导数的均值均方误差均呈现减小的趋势，但其减小量不大，这主要是场值幅值减少的缘故.而归一化均值均方误差变化规律却不相同，当场源体埋深增大时，磁力异常归一化均值均方误差变化不大；化极磁力异常归一化均值均方误差呈现增大的趋势；化极磁力异常垂向一阶导数归一化均值均方误差呈现先减小后增大的抛物线规律.
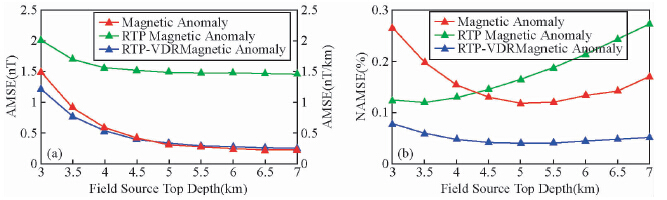 | 图 6 不同埋深场源在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差;(b)归一化均值均方误差. Fig. 6 The processing and transforming results error map on z=-2.0 km plane by different field source top depths model(a)Average mean square error;(b)Normalized average mean square error. |
为了试验场源水平尺寸对频率域偶层位法的影响，选用基本模型二，直立六面体模型顶面z坐标为3.0 km，改变该模型水平宽度保持中心位置不变，将其在x、y两个方向上的宽度分别增大0.0 km(同基本模型二)、1.0 km、2.0 km、3.0 km、4.0 km、5.0 km和6.0 km，此时直立六面体的水平宽度分别为8.0 km、9.0 km、10.0 km、11.0 km、12.0 km、13.0 km和14.0 km.计算了z=-2.0 km平面上的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数，并进行了均值均方误差和归一化均值均方误差统计(图 7).从误差统计结果来看，当模型体水平宽度增大时，磁力异常和化极磁力异常垂向一阶导数的均值均方误差变化不大，而化极磁力异常均值均方误差出现增大趋势，这主要是场值幅值增大的缘故.而归一化均值均方误差不论是磁力异常、化极磁力异常或化极磁力异常垂向一阶导数均呈现增加趋势，但变化量很小.
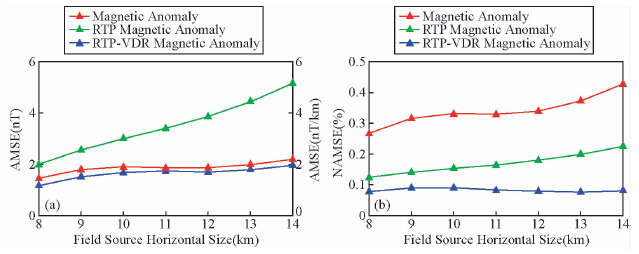 | 图 7 不同水平尺寸场源在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差;(b)归一化均值均方误差. Fig. 7 The processing and transforming results error map on z=-2.0 km plane by different horizontal size field source model(a)Average mean square error;(b)Normalized average mean square error. |
为了试验不同场源组合对频率域偶层位法的影响，本次试验选用基本模型三，并改变三个直立六面体的平面相对位置进行试验.保持2号和4号直立六面体位置不变，使3号直立六面体沿x轴和y轴正方向分别移动0.0 km(同基本模型三)、1.0 km、2.0 km、3.0 km、4.0 km、5.0 km、6.0 km和7.0 km.计算了z=-2.0 km平面上磁力异常、化极磁力异常和化极磁力异常垂向一阶导数，并进行了均值均方误差和归一化均值均方误差统计(图 8).由图 8可以看出，当场源相对位置改变时，磁力异常和化极磁力异常垂向一阶导数的均值均方误差变化不大，化极磁力异常均值均方误差呈现某种增大趋势.而归一化均值均方误差不论是磁力异常、化极磁力异常或化极磁力异常垂向一阶导数均变化不大.
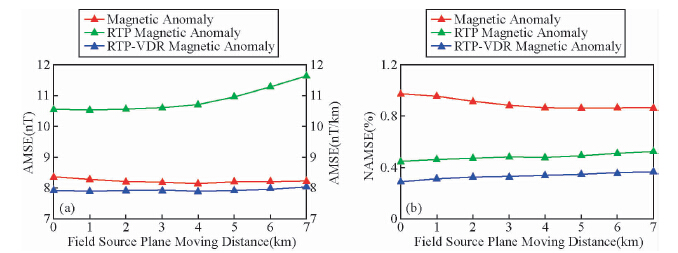 | 图 8 不同组合场源在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差；(b)归一化均值均方误差. Fig. 8 The processing and transforming results error map on z=-2.0 km plane by different plane position combination model(a)Average mean square error;(b)Normalized average mean square error. |
由以上场源分布试验可以看到，频率域偶层位法基本不受场源埋深、水平尺寸和组合的影响，而只受“强地形”和“弱地形”的影响，“强地形”越强，其影响越大.也就是说，频率域偶层位法受场源分布的影响较小，受地形起伏的影响较大.一般来说，只能适用于“弱地形”，而不能用于“强地形”，对较弱的“强地形”可近似使用. 3 观测面起伏影响试验
观测面起伏包括连续观测面和不连续(间断)观测面两种情况，下面分别就这两种情况进行测试.
3.1 连续观测面影响试验
均匀连续观测面是指测点均匀分布在一近似的连续曲面上.这部分试验包括等间距和不等间距试验以及不同起伏(坡度)试验三个方面.
3.1.1 不同网格(等间距)影响试验
为了研究观测面不同网格(等间距)对频率域偶层位法的影响，选用基本模型三.网格间距分别选为0.5 km、1.0 km、2.0 km和4.0 km四个值进行试验.计算了z=-2.0 km平面上的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数，并进行了均值均方误差和归一化均值均方误差统计(图 9).由图 9误差统计结果可以看出，当网格间距增大时，磁力异常均值均方误差和归一化均值均方误差呈现减小的趋势，而化极磁力异常及其垂向一阶导数误差呈现先减小后增大的趋势.误差变化最大的是间距大于2.0 km时的化极磁力异常及其垂向一阶导数，这主要是由于间距增大后，其对磁力异常的分辨能力下降，即截止频率减小，折叠效应增强所致，致使化极磁力异常及其垂向一阶导数的计算精度也就下降.
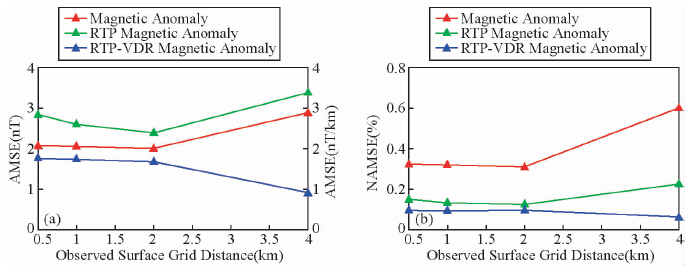 | 图 9 不同网格(等间距)观测面在z=-2.0 km平面上处理和转换结果误差分布图
(a)均值均方误差；(b)归一化均值均方误差. Fig. 9 The processing and transforming results error map on z=-2.0 km plane by different grid distance(equal spacing)model(a)Average mean square error;(b)Normalized average mean square error. |
为了研究观测面不同网格(不等间距)对频率域偶层位法的影响，选用基本模型三.观测面以0.5 km为点距(x方向)，分别以0.5 km、1.0 km、2.0 km和4.0 km为线距(y方向)进行不同网格不等间距影响试验.当观测面线距为0.5 km和1.0 km时可以选择适当的偶层面位置进行偶层面面密度反演，并在此基础上进行曲面位场处理和转换，对计算结果的均值均方误差和归一化均值均方误差进行了统计(表 2).可以看出当线距增大时，磁力异常、化极磁力异常和化极磁力异常垂向一阶导数曲面处理和转换结果的均值 均方误差和归一化均值均方误差变化很小.而当线距为2.0 km和4.0 km时，反演计算偶层面面密度时出现发散，无法得到偶层面面密度结果.从试验结果可以得知，当线距小于4倍点距时，磁力异常、化极磁力异常和化极磁力异常垂向一阶导数的均值均方误差和归一化均值均方误差均减小，但变化量很小；而当线距大于4倍点距时，频率域偶层位法反演计算偶层面面密度发散.因此，频率域偶层位曲面处理和转换方法在使用时尽量保持点距和线距相等为好，即使不等也不要变化很大，保持在2倍左右即可.
| | 表 2 不同网格(不等间距)在z=-2.0 km平面上的处理和转换结果误差统计表 Table 2 The processing and transforming results error statistics table on z=-2.0 km plane by different grid distance(unequal spacing)model |
为了研究观测面起伏(坡度)对频率域偶层位法的影响，利用基本模型三设计了平均平面为z=-2.0 km，观测面起伏差为1.0～7.0 km(对应的坡度角为1.088°～7.688°)，每隔1.0 km分别设计了7个不同起伏观测面.各起伏观测面是在基本模型三观测面的基础上保持平均平面不变，按比例调整观测面的z坐标而形成.
利用频率域偶层位法分别计算了不同起伏观测面在z=-2.0 km平面(平均平面)上的磁力异常，化极磁力异常和化极磁力异常垂向一阶导数，并进行了均值均方误差和归一化均值均方误差统计(图 10).由图 10可以看到随着观测面坡度的增大，频率域偶层位法曲面处理和转换得到的磁力异常、化极磁力异常和化极磁力异常垂向一阶导数的均值均方误差和归一化均值均方误差均呈线性增大趋势.
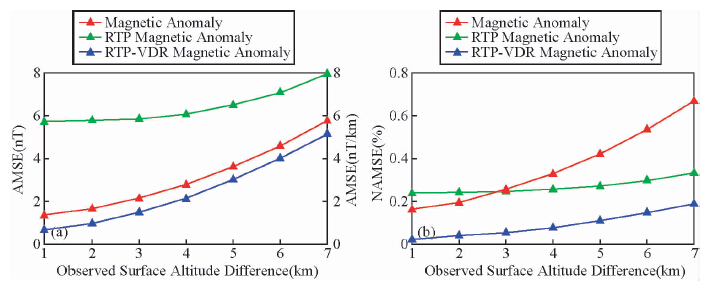 | 图 10 不同起伏(坡度)观测面在z=-2.0
(a)均值均方误差；(b)归一化均值均方误差. Fig. 10 The processing and transforming results error map on z=-2.0km plane by different rolling distance(slope)observing surface model(a)Average mean square error;(b)Normalized average mean square error. |
不连续观测面包括水平不连续观测面、垂向不连续观测面以及水平重叠观测面三种情况.这三种情况均是用来模拟不同时期数据拼接之后的曲面处理和转换问题.水平不连续观测面是指观测面整体是连续的，但每块之间存在较大的空白区；垂向不连续观测面是指每块之间存在较大的垂向距离，但每块内部是连续的；水平重叠观测面是指每块观测面内部是连续的，但每块之间存在部分水平位置的重叠及垂向位置的高差变化. 3.2.1 水平不连续观测面影响试验
将基本模型三的观测面以x=0.0 km为界分成东、西两块，东、西两块之间的空白区域间距分别为0.0 km(同基本模型三)、0.5 km、1.0 km、1.5 km、2.0 km、2.5 km和3.0 km.分别对不同空白区域间距的观测面进行曲面处理和转换，并对z=-2.0 km平面上的曲面处理和转换结果统计其均值均方误差和归一化均值均方误差(图 11).由图 11可以看到，随着空白区域的增大，曲面处理和转换得到的磁力异常、化极磁力异常及其垂向一阶导数的均值均方误差和归一化均值均方误差逐渐增大，且在空白区域间距大于 4.0 km以上时误差增加较快.这是由于空白区域越大，其截止频率越小造成的.由于观测面存在空白区域，故在频率域中进行曲面位场处理和转换时需要把空白区域位场数据补空(王万银等，2009).空白区域越大，需要补空的数据越多，计算结果的误差也就越大.
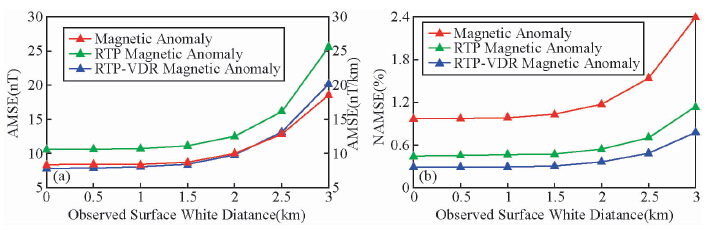 | 图 11 不同空白区域观测面在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差，(b)归一化均值均方误差图. Fig. 11 The processing and transforming results error map on z=-2.0 km plane by different white distance observing surface model(a)Average mean square error;(b)Normalized average mean square error. |
将基本模型三观测面以x=0.0 km为界分成东、西两块，东部的观测面在原观测面的基础上抬高了0.0 km(同基本模型三)、0.5 km、1.0 km、1.5 km、2.0 km、2.5 km和3.0 km.分别对不同垂向不连续观测面进行曲面处理和转换试验，并对z=-2.0 km平面上的磁力异常、化极磁力异常及其垂向一阶导数的均值均方误差和归一化均值均方误差进行了统计(图 12).由图 12可以看到，随着垂向不连续观测面距离的增大，不论是磁力异常、化极磁力异常或化极磁力异常垂向一阶导数的均值均方误差和归一化均值均方误差均呈增大趋势，且该误差要比水平不连续观测面的误差大很多.这主要是在垂向不连续观测面处，垂向距离越大其在Fourier变换时产生的Gibbs效应越大，从而使得曲面位场处理和转换结果的误差越大.
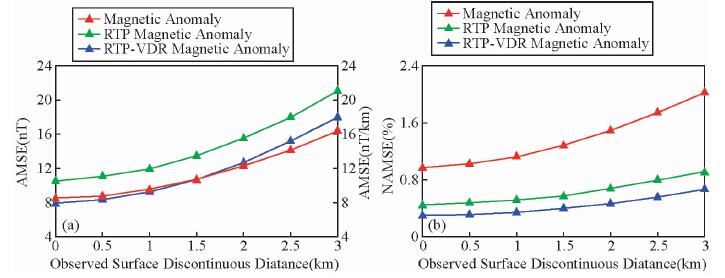 | 图 12 不同垂向不连续观测面在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差;(b)归一化均值均方误差. Fig. 12 The processing and transforming results error map on z=-2.0 km plane by different discontinuous distance observing surface model(a)Average mean square error;(b)Normalized average mean square error. |
作为垂向不连续观测面的一个特例就是航磁飞行观测面.在基本模型三上，将y方向每隔3.0 km其前后两侧观测面分别抬高和降低0.0 km(同基本模型三)、0.2 km、0.4 km、0.6 km、0.8 km、1.0 km、1.2 km、1.4 km、1.6 km、1.8 km和2.0 km.为了使所有观测点位于场源之上，将基本模型三中三个直立六面体埋深均增大3.0 km，其它参数保持不变.运用频率域偶层位法对不同测线高差变化观测面进行曲面处理和转换，对计算结果进行了均值均方误差和归一化均值均方误差统计(图 13).由图 13可以看出，当测线高差小于等于1.0 km(2个点距)时，不论是均值均方误差或归一化均值均方误差均变化不大；但当测线高差大于1.0 km(2个点距)时，不论是均值均方误差或归一化均值均方误差均呈现快速增大的趋势.这主要是由于垂向高差越大，其Fourier变换时的Gibbs效应越明显所造成的.
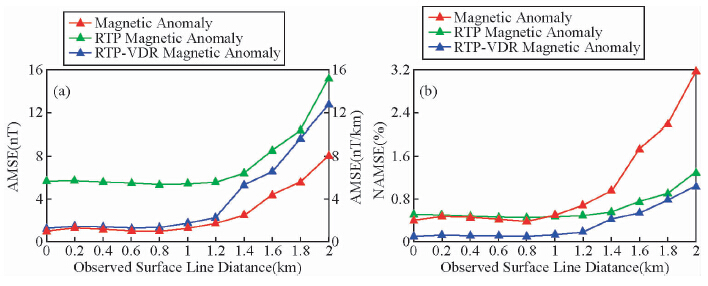 | 图 13 不同测线高差变化在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差;(b)归一化均值均方误差. Fig. 13 The processing and transforming results error map on z=-2.0 km plane by different height measuring line observing surface model(a)Average mean square error;(b)Normalized average mean square error. |
水平重叠观测面是指在垂向上存在不连续，在水平上有重叠的情况.当无水平重叠时就是垂向不连续观测面的情况，当无垂向不连续且观测面之间存在空白区域时就是水平不连续观测面的情况.频率域偶层位法还不能直接处理水平重叠观测面的情况，若要近似处理就是将其重叠部分数据截断，按照垂向不连续观测面的情况进行处理.所以，频率域偶层位法不能进行水平重叠观测面的曲面位场处理和转换.
由以上观测面起伏试验结果表明，除水平重叠观测面外，频率域偶层位法可用于连续观测面和不连续(间断)观测面的曲面位场处理和转换.对于连续观测面，随着网格间距的增大和坡度角的增大其误差呈现增大趋势，并保持网格点距和线距相等时误差最小.对于不连续观测面，主要受垂向不连续观测面的影响较大，受水平不连续观测面的影响较小. 4 稳定性试验
为了测试频率域偶层位法的稳定性，采用基本模型三，在原观测面磁力异常中加入均值为0.0 nT，标准差分别为0.0 nT(同基本模型三)、5.0 nT、10.0 nT、15.0 nT、20.0 nT、25.0 nT、30.0 nT、35.0 nT和40.0 nT的随机干扰.根据加入不同随机干扰的观测面磁异常进行曲面位场处理和转换，其在z=-2.0 km平面上的磁力异常、化极磁力异常及其垂向一阶导数均值均方误差和归一化均值均方误差统计结果见图 14所示.由图 14可以看到，随着随机干扰标准差的增大，曲面位场处理和转换结果的误差也在增大，但变化不大.这说明频率域偶层位法具有很好的稳定性.
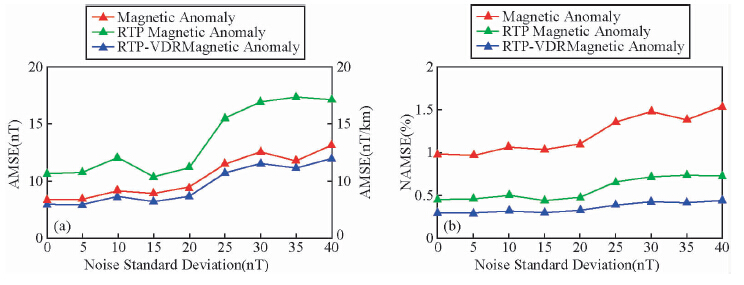 | 图 14 不同随机干扰在z=-2.0 km平面上的处理和转换结果误差分布图
(a)均值均方误差，(b)归一化均值均方误差. Fig. 14 The processing and transforming results error map on z=-2.0 km plane by adding different r and om noise(a)Average mean square error;(b)Normalized average mean square error. |
本文对频率域偶层位曲面位场处理和转换方法从场源分布和观测面起伏两个方面研究了其适应性及计算精度；从不同随机干扰大小测试了其稳定性，得出以下结论：
(1)频率域偶层位法不能应用于“强地形”、重叠观测面以及点/线距较大或者点距与线距差别较大的情况，其他情况均可以使用.该方法受垂向不连续观测面的影响最大、其次是点距和线距大小的影响、而受场源分布的影响最小，并且受随机干扰的影响也较小.
(2)将来需要重点研究频率域偶层位法当点距/线距增大时，点距与线距的比例增大时以及垂向不连续间距增大时的计算精度，使频率域偶层位曲面位场处理和转换方法更加完善.
致 谢 感谢潘作枢教授对本文提出的修改意见，也感谢论文评审专家提出的修改意见.| [1] | Bhattacharyya B K, Chen K C. 1977. Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief[J]. Geophysics, 42(7): 1411-1430, doi: 10.1190/1.1440802. |
| [2] | Chen Z Q. 1983. Principle and computational method of curved surface's continuation of potential field for equivalently dipolar layer's method [J]. Chinese J. Geophys. (in Chinese), 26(1): 70-79. |
| [3] | Dampney C N G. 1969. The equivalent source technique[J]. Geophysics, 34(1): 39-53, doi: 10.1190/1.143996. |
| [4] | Du W B. 1982. A new method of reducing from an arbitrary surface into a plane for the three dimensional magnetic and gravity field[J]. Chinese J. Geophys. (in Chinese), 25(1): 73-83. |
| [5] | Emilia D A. 1973. Equivalent sources used as an analytic base for processing total magnetic field profiles[J]. Geophysics, 38(2): 339-348, doi: 10.1190/1.1440344. |
| [6] | Guan Z N, An Y L, Chen W X. 1985. Upward continuation and transformation of component of magnetic field on an undulating observed profile or surface[J]. Chinese J. Geophys. (in Chinese), 28(4): 419-428. |
| [7] | Handerson R G, Cordell L. 1971. Reduction of unevenly spaced potential field data to a horizontal plane by means of finite harmonic series[J]. Geophysics, 36(5): 856-866, doi: 10.1190/1.1440220. |
| [8] | Hansen R O, Miyazaki Y. 1984. Continuation of potential field between arbitrary surfaces[J]. Geophysics, 49(6): 787-795, doi: 10.1190/1.1441707. |
| [9] | Hou Z C, Cai Z X, Liu K J. 1985a. Interpretation system of potential field transformation on an uneven surface from the potential of double layler[J]. Chinese J. Geophys. (in Chinese), 28(4): 410-418. |
| [10] | Hou Z C, Cai Z X, Liu K J. 1985b. Establishing and interpretation system of potential field transformation on an uneven surface from the potential of a single layer[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 7(1): 1-12. |
| [11] | Hou J S,Guan Z N. 1995. Method of frequency domain for reduction to a plane using the potential field and its gradients[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 17(4): 60-66. |
| [12] | Liang J W. 1988. Surface continuation method of finite spherical harmonics potential fields[J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 10(3): 203-210. |
| [13] | Liu J L, Wang W Y, Yu C C. 2007. Reduction of potential field data to a horizontal plane by a successive approximation procedure[J]. Chinese J. Geophys. (in Chinese), 50(5): 1551-1557. |
| [14] | Nakatsuka T. 1981. Reduction of magnetic anomalies to and from an arbitrary surface[J]. Geophysical Exploration, 34(5): 6-13. |
| [15] | Pilkington M, Urquhartt W E S. 1990. Reduction of potential field data to a horizontal plane[J]. Geophysics, 55(5): 549-555, doi: 10.1190/1.1442866. |
| [16] | Wang W Y, Pan Z S. 1996. Data processing and transformation methods of potential fields on an arbitray surface with dipole layer potential technique[J]. Journal of Xi'an College of Geology (in Chinese), 18(3): 69-76. |
| [17] | Wang W Y, Pan Z S. 1997. The trigonometric function methods for data-processing and transform of curved surface potential field[J]. Geophysical & Geochemical Exploration (in Chinese), 21(3): 209-218. |
| [18] | Wang W Y, Liu J L, Qiu Z Y, et al. 2009. The research of the frequency domain dipole layer method for the processing and transformation of potential field on curved surface[J]. Chinese J. Geophys. (in Chinese), 52(10): 2652-2655, doi: 10.3969/j.issn.0001-5733.2009.10.026. |
| [19] | Wang W Y, Qiu Z Y, Liu J L, et al. 2009. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing[J]. Progress in Geophys. (in Chinese), 24(4): 1327-1338, doi: 10.3969/j.issn.1004-2903.2009.04.022. |
| [20] | Xia J H, Sprowl D R. 1991. Correction of topographic distortion in gravity data[J]. Geophysics, 56(4): 537-541, doi: 10.1190/1.1443070. |
| [21] | Xia J H, Sprowl D R, Adkins-Heljeson D. 1993. Correction of topographic distortion in potential-field data: A fast and accurate approach[J]. Geophysics, 58(4): 515-523, doi: 10.1190/1.1443434. |
| [22] | Xu L X. 1988. Integral continuation calculation method for three dimensional gravity and magnetic field[J]. Geophysical & Geochemical Exploration (in Chinese), 12(2): 91-98. |
| [23] | Xu S Z, Dai S K, Lan X. 2002. A new fast method for continuation of potential field on an undulate terrain[J]. Geological Journal of China Universities (in Chinese), 8(3): 241-247. |
| [24] | Yang Z C. 1989. The Datuming of gravitational potential fields with the use of iteration method[J]. Oil Geophysical Prospecting (in Chinese), 24(2): 200-207, 216. |
| [25] | Yao C L, Huang W N, Guan Z N. 1997. Fast splines conversion of curved-surface potential field and vertical gradient data into horizontal-plane data[J]. Oil Geophysical Prospecting (in Chinese), 32(2): 229-236. |
| [26] | Yu C C, Wang W Y, Fan Z G, et al. 2007. The application of the frequency domain dipole layer method to the processing of aeromagnetic data surreyed by helicopter[J]. Geophysical and Geochemical Exploration (in Chinese), 31(6): 577-580. |
| [27] | 陈钟琦. 1983. 等效偶层法位场曲面延拓的原理和计算方法[J]. 地球物理学报, 26(1): 70-79. |
| [28] | 杜维本. 1982. 三维重磁场“曲化平”的一个方法[J]. 地球物理学报, 25(1): 73-83. |
| [29] | 管志宁, 安玉林, 陈维雄. 1985. 曲线与曲面上磁场向上延拓和分量转换[J]. 地球物理学报, 28(4): 419-428. |
| [30] | 管志宁, 安玉林, 陈维雄. 1985. 曲线与曲面上磁场向上延拓和分量转换[J]. 地球物理学报, 28(4): 419-428. |
| [31] | 侯重初, 蔡宗熹, 刘奎俊. 1985a. 从偶层位出发建立曲面上的位场转换解释系统[J]. 地球物理学报, 28(4): 410-418. |
| [32] | 侯重初, 蔡宗熹, 刘奎俊. 1985b. 从单层位出发建立曲面上的位场转换解释系统[J]. 物化探计算技术, 7(1): 1-12. |
| [33] | 候俊胜, 管志宁. 1995. 综合利用位场及其梯度的频率域曲化平方法[J]. 物探化探计算技术, 17(4): 60-66. |
| [34] | 梁锦文. 1988. 有限球谐位场曲面延拓方法[J]. 物探化探计算技术, 10(3): 203-210. |
| [35] | 刘金兰, 王万银, 于长春. 2007. 逐步逼近曲化平方法研究[J]. 地球物理学报, 50(5): 1551-1557. |
| [36] | 王万银, 潘作枢. 1996. 偶层位曲面位场数据处理及转换方法[J]. 西安地质学院学报, 18(3): 69-76. |
| [37] | 王万银, 潘作枢. 1997. 曲面位场数据处理及转换的三角函数法[J]. 物探与化探, 21(3): 209-218. |
| [38] | 王万银, 刘金兰, 邱之云,等. 2009a. 频率域偶层位曲面位场处理和转换方法研究[J]. 地球物理学报, 52(10): 2652-2655, doi: 10.3969/j.issn.0001-5733.2009.10.026. |
| [39] | 王万银, 邱之云, 刘金兰,等. 2009b. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 24(4): 1327-1338, doi: 10.3969/j.issn.1004-2903.2009.04.022. |
| [40] | 徐连喜. 1988. 三维重磁场积分延拓计算方法[J]. 物探与化探, 12(2): 91-98. |
| [41] | 徐世浙, 戴世坤, 兰翔. 2002. 起伏地形位场快速延拓新方法[J]. 高校地质学报, 8(3): 241-247. |
| [42] | 杨再朝. 1989. 应用迭代法进行位场的曲化平[J]. 石油地球物理勘探, 24(2): 200-207, 216. |
| [43] | 姚长利, 黄卫宁, 管志宁. 1997. 综合利用位场及其垂直梯度的快速样条曲化平方法[J]. 石油地球物理勘探, 32(2): 229-236. |
| [44] | 于长春, 王万银, 范正国,等. 2007. 频率域偶层位方法在直升机磁测数据处理中的应用[J]. 物探与化探, 31(6): 577-580. |