随着油气勘探开发难度的逐年加大,对地震资料处理的“三高”要求越来越高,而提高资料的信噪比是地震资料处理的首要任务(张军华等,2006;毕丽飞等,2008),噪音的衰减是提高信噪比、高精度成像的基础.通常情况下,转换波资料信噪比和纵波相比要低很多,同时转换波的有效波主频也比纵波要低,而转换波特有的反射机理,使得面波的发育范围广泛,成为转换波记录的主要干扰(李国发等,2005;刘洋和魏修成,2006),由于转换波和面波的速度和频率都较低,造成有效波和面波等低频干扰的速度和频率重叠现象,这就使得转换波去除低频噪音变得异常困难.目前,纵波的去噪方法已经相对成熟,出现了许多新的方法,在去除低频干扰等方面也取得一定的效果(Hennenfent and Herrmann,2006;Ran et al.,2008;孟小红等,2008;Pei and Ding,2010;汪铁望等,2010;沈鸿雁和李庆春,2010;Jin,2010;Mao et al.,2010;刘洋等,2011;彭建亮等,2012;张华和陈小宏,2013;陈文超等,2013),像小波变换分频去噪(张华等,2007;张旭东等,2007;陈文超等,2009;覃天,2009;柳建新等,2010),基于S变换的去噪(Rober Pinnegar and Mansinha,2003;李雪英等,2011),F-X域去噪(王兆湖等,2013)、Radon变换去噪(Wang et al.,2010),极化滤波去噪等已经开始应用于纵波(刘春园和徐胜峰,2009),但是转换波资料的信噪比更低,噪声波场更加的复杂,使得许多纵波的去噪方法不再适用.因此,在转换波压制低频干扰方面,还需要进一步研究切实可行的方法.
胜利油区工农业发达,公路网密布,干扰比较多,又由于单点数字检波器接收及其高灵敏度的特点使得周围环境噪音的影响尤其突出,使得噪音波场复杂(仲伯军等,2013),特别是面波比较发育,且能量较强,造成整体转换波资料的信噪比和分辨率较低,常规的去噪方法无法有效地去除这种具有非双曲特征的强面波干扰,利用类似于压制纵波资料中噪声的方法进行处理,将会明显丢失大量的有效信号,尤其是当规则干扰能量比较强,分布范围较广,去除效果就很不理想.因此,为提高信噪比和成像质量,生产中急需要切实可行的三维转换波资料矢量去噪软件. 1 转换波自适应矢量去噪技术原理 1.1 转换波噪音特征
转换波具有不同于纵波的反射路径,因此其噪音的特点也不同于纵波,不能把纵波的去噪方法简单的应用于转换波,必须先充分认识转换波噪音的传播机理及反射特征,以便采取针对性的措施进行压制(韩文功等,2011).
胜利探区某区块原始炮记录如图 1所示:可以看到:X分量面波干扰波能量更强,Y分量次之,Z分量最弱,X分量面波的范围明显强于Z分量,且呈非双曲分布.
 | 图 1 原始炮记录
(a)X分量;(b)Y分量;(c)Z分量. Fig. 1 The original shot records(a)X component;(b)Y component;(c)Z component. |
应用分频扫描、频谱分析等调查噪音的视速度范围及频率的横向变化情况,如图 2、3,可以看到:转换波和面波能量主要集中在低频段,有效波频带主要集中在0~30 Hz,面波频带主要集中在0~20 Hz,两者频带有部分重叠,给面波去除带来较大困难.
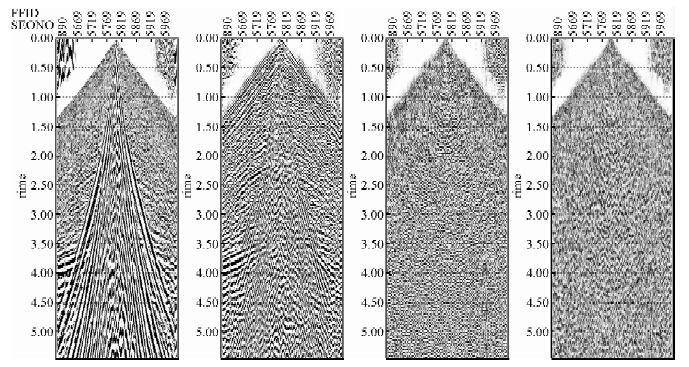 | 图 2 分频扫描Fig. 2 Frequency scanning |
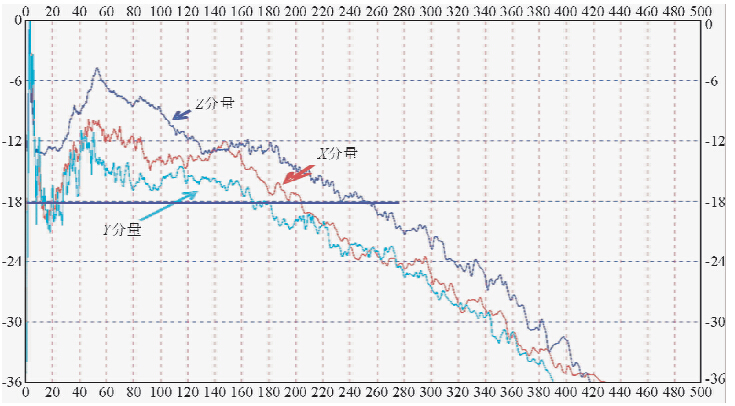 | 图 3 X-Y-Z频谱分析Fig. 3 Frequency scanning |
该方法是一种自适应的叠前规则干扰压制技术,在时空域采用逐点多道识别单道计算的方法来识别各种倾角的规则噪声,并采用中值滤波和预测滤波对检测到的规则噪声进行压制.
1)假设沿某一斜率P的规则噪声 N(p,t),对沿检波器方向排列的各道数据进行采样,可以得到一维信号:
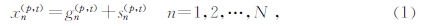
因此,如果能从xn(p,t)分解出gn(p,t)与 sn(p,t),也就分解出了记录上的规则噪声.
2)由于地震记录中的规则噪声gn(p,t)一般是呈近似线性分布的,而有效信号及其它噪声sn(p,t)的样点值在沿着规则噪声的同相轴方向则呈随机分布,因此可以在xn(p,t)寻找具有规则分布的地震样点值来达到寻找到规则噪声的分布.
对于地震记录的时间序列xn-1(p,t),若xn-m(p,t)为过去M个值对现在值xn(p,t)所作的线性预测值,则有:
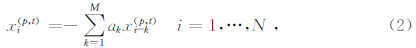
3)预测误差则为:
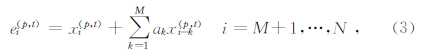
4)对叠前记录上任意一点(i0,j0),逐点扫描叠加能量:
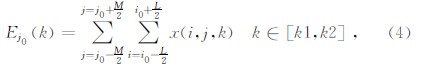
5)按叠加能量最大法确定噪声的倾角:
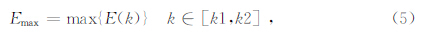
轴的倾角.
6)假设所给定的规则干扰的同相轴的倾角范围是[a1,a2],令:
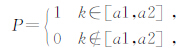
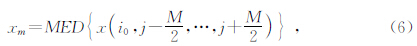
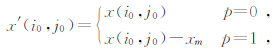
该方法的技术特色:
1)采用逐点预测,信号保真度高,信号的畸变较小,克服了F-K法压制规则噪声的弱点;
2)针对转换波资料主频较低的特点设计;
3)自适应噪声倾角变化,不需要人为干预;
4)适应于三维转换波数据;计算效率高.
2 应用效果
图 4是三维理论模型去噪后的效果,可以看到应用本方法后可以有效去除噪音,如图 4b和4c所示炮记录的噪音去除的较干净,去除的噪音也较完全.
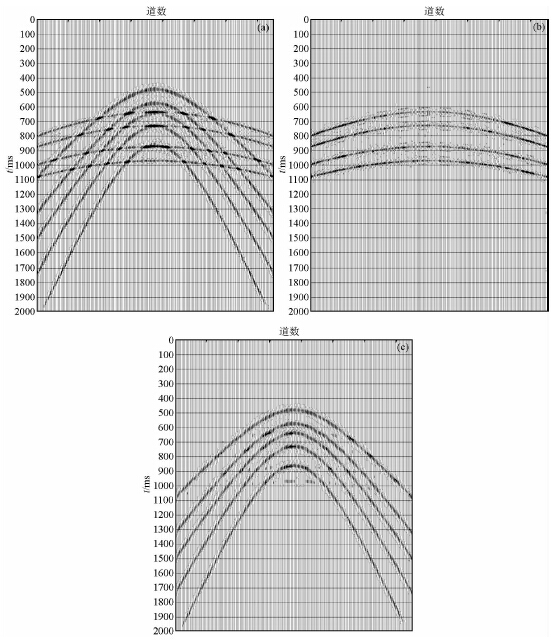 | 图 4 模型炮记录去噪效果对比
(a)原始三维炮记录;(b)本方法分离出的反射信号;(c)本方法分离出的噪音. Fig. 4 Model shot record denoising effect comparison(a)The original 3D shot record;(b)Separating the reflected signal of the method;(c)Separating the noise of the method |
图 5是罗家三维转换波炮记录的去噪后的效果,进行去噪时,要分步进行去噪,通过设定视速度范围,分频带分多次进行噪音压制.如图 5b和5c所示为第一次进行噪音压制效果,可以看到第一次噪音压制后去除了大部分的面波等低频干扰,如图 5d和5e所示为在第一次进行噪音压制的基础上进行第二次噪音压制的效果,可以看到第二次压制了部分的高频噪音,如图 5f所示为在第二次进行噪音压制的基础上进行第三次噪音压制的效果,可以看到第三次进行了反向干扰的压制.
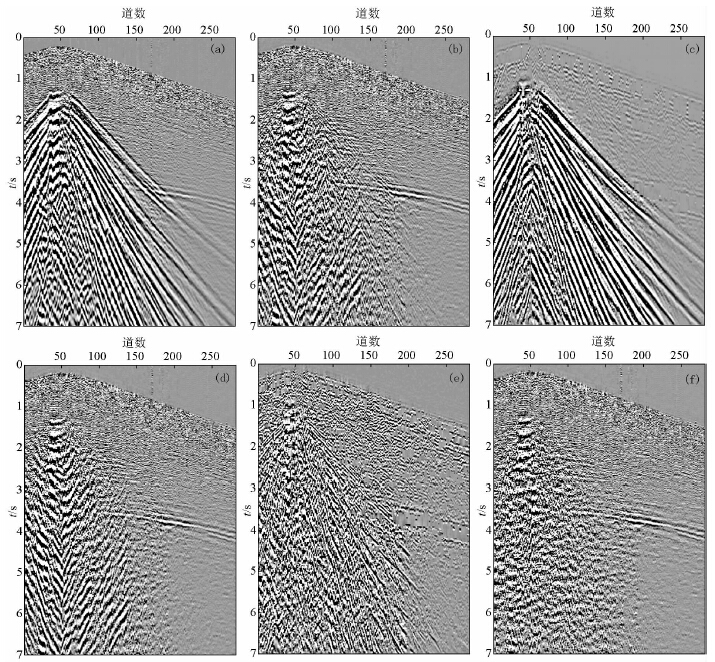 | 图 5 三维转换波炮记录去噪效果
(a)转换波原始炮记录;(b)第一次噪音衰减后的炮记录;(c)第一次衰减的噪音;(d)第二次噪音衰减后的炮记录;(e)第二次衰减的噪音;(f)第三次噪音衰减后的炮记录. Fig. 5 The denoising effect of 3D converted wave shot records(a)The original shot records of converted wave;(b)The shot records of the first attenuation;(c)The noise of the first attenuation;(d)The shot records of the second attenuation;(e)The noise of the second attenuation;(f)The shot records of the third attenuation. |
对罗家数据处理结果图 6,通过叠加剖面可看到,面波及其它低频噪音都得到了去除,噪音压制效果理想,压制后剖面的分辨率明显提高,同相轴更加连续.
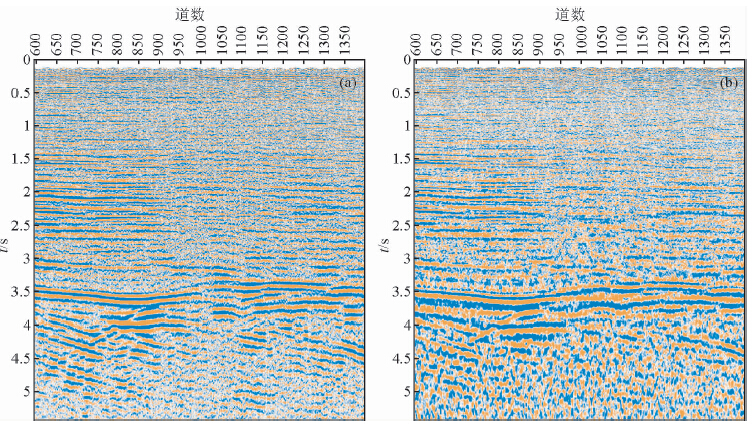 | 图 6 转换波噪音衰减前后叠加剖面对比
(a)转换波去噪后的叠加剖面;(b)转换波去噪前的叠加剖面. Fig. 6 The denoising effect comparison of the converted wave stack section(a)The stack section after denoising;(b)The stack section before denoising. |
该方法针对转换波资料主频较低的特点设计,采用逐点多道识别单道计算,信号保真度高,信号的畸变较小,克服了F-K等常规方法压制规则噪声的弱点,既可以压制炮集、检波点道集上的面波干扰,也可以压制成像剖面的上的规则干扰,能有效提高地震数据的信噪比和分辨率,即可用于三维数据,也可用于二维数据,自适应噪声倾角变化,不需要人为干预,计算效率高,适应大规模实际生产的需要,在胜利垦71以及罗家等区块去的不错的实际应用效果.
但是在复杂的地表地质条件下,转换波资料噪音干扰严重,类型丰富,仅靠某一种方法难以去除各种干扰,而且即使是单一噪音,也无法用一种方法完全去除,因此,在对每一种噪音特征进行充分认识的基础上,也需要通过不同域,不同去噪算法联合应用,循序渐进的消除干扰,并在保幅的前提下最大限度地压制噪音.
致 谢 感谢审稿专家提出的宝贵修改意见和编辑部老师的帮助.| [1] | Bi L F, Meng X J, Feng G, et al. 2008. Study on 3D converted wave data processing method and application[J]. Oil Geophysical Prospecting (in Chinese), 43(S2): 150-154. |
| [2] | Chen W C, Gao J H, Bao Q Z. 2009. Adaptive attenuation of ground roll via continuous wavelet transform[J]. Chinese Journal of Geophysics (in Chinese), 52(11): 2854-2861. |
| [3] | Chen W C, Wang W, Gao J H. 2013. Sparsity optimized separation of Ground-roll noise based on morphological diversity of seismic waveform components[J]. Chinese J. Geophys. (in Chinese), 56(8): 2771-2782, doi: 10.6038/cjg20130825. |
| [4] | Han W G, Yu J, Zhang H B, et al. 2011. Application of interference wave investigation methods in high-density seismic acquisition[J]. Geophysical Prospecting for Petroleum (in Chinese), 50(5): 499-507. |
| [5] | Hennenfent G, Herrmann F J. 2006. Seismic denoising with nonuniformly sampled curvelets[J]. Computing in Science & Engineering, 8(3): 16-25. |
| [6] | Jin S. 2010. 5D seismic data regularization by a damped least-norm Fourier inversion[J]. Geophysics, 75(6): WB103-WB111. |
| [7] | Li G F, Peng S P, Gao R S, et al. 2005. Suppression the ground roll in converted wave seismic data[J]. GPP (in Chinese), 44(3): 214-216. |
| [8] | Li X Y, Sun D, Hou X H, et al. 2011. Comparison of generalized S transform and empirical mode decomposition in high frequency seismic noise suppression[J]. Progress in Geophysics (in Chinese), 26(6): 2039-2045, doi: 10.3969/j.issn.1004-2903.2011.06.019. |
| [9] | Liu C Y, Xu S F. 2009. Research on the three-component noise attenuation through polarization filtering[J]. Progress in Geophys. (in Chinese), 24(5): 1814-1823, doi: 10.3969/j.issn.10042903.2009.05.036. |
| [10] | Liu J H, Liu F T, Xu Y. 2006. Polarization analysis of three-component seismic data[J]. Progress in Geophysics (in Chinese), 21(1): 6-10. |
| [11] | Liu J X, Li J, Yang J. 2010. The application of modified Wavelet frequency division restructuring to petrol seismic survey data processing[J]. Progress in Geophysics (in Chinese), 25(6): 2009-2014, doi: 10.3969/j.issn.1004-2903.2010.06.016. |
| [12] | Liu Y, Wei X C. 2006. Seismic processing method of 3D converted wave[J]. Natural Gas Industry (in Chinese), 26(12): 72-74. |
| [13] | Liu Y, Wang D, Liu C, et al. 2011. Weighted median filter based on local correlation and its application to poststack random noise attenuation[J]. Chinese J. Geophys. (in Chinese), 54(2): 358-367, doi: 10.3969/j.issn.0001-5733.2011.02.012. |
| [14] | Liu Z P, Chen X H, Li J Y. 2008. Study on coherent noise attenuation using radial trace transform filtering[J]. Progress in Geophysics (in Chinese), 23(4): 1199-1204. |
| [15] | Mao J, Wu R S, Gao J H. 2010. Directional illumination analysis using the local exponential frame[J]. Geophysics, 75(4): S163- S174. |
| [16] | Meng X H, Guo L H, Zhang Z F, et al. 2008. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform[J]. Chinese J. Geophys. (in Chinese), 51(1): 235-241. |
| [17] | Pei S C, Ding J J. 2010. Fractional fourier transform, wigner distribution, and filter design for stationary and nonstationary random processes[J]. IEEE Transaction on Signal Processing, 58(8): 4079-4092. |
| [18] | Peng J L, Peng Z M, Zhang J, et al. 2012. De-noising method of seismic signal based on adaptive filtering in fractional domain[J]. Progress in Geophys. (in Chinese), 27(4): 1730-1737, doi: 10.6038/j.issn.100402903.2012.04.054. |
| [19] | Qin T. 2009. Prestack coherent noise attenuation based on wavelet frequency-division[J]. Progress in Geophys. (in Chinese), 24(4): 1426-1430. |
| [20] | Ran T, Deng B, Zhang W Q, et al. 2008. Sampling and sampling rate conversion of band limited signals in the fractional fourier transform domain[J]. IEEE Transactions on Signal Processing, 56(1): 158-171. |
| [21] | Rober Pinnegar C, Mansinha L. 2003. The S -transform with windows of arbitrary and varying shape[J]. Geophisics, 68(1): 381-385. |
| [22] | Shen H Y, Li Q C. 2010. New idea for seismic wave filed separation and denoising by singular value decomposition(SVD)[J]. Progress in Geophysics (in Chinese), 25(1): 225-230, doi: 10.3969/j.issn.1004-2903.2010.01.030. |
| [23] | Wang J F, Ng M, Perz M. 2010. Seismic data interpolation by greedy local Radon transform[J]. Geophysics, 75(6): WB225-WB234. |
| [24] | Wang T W, Yu X H, Hu H, et al. 2010. Attenuation of coherent noise in seismic data coith crooked line geometry[J]. Progress in Geophysics (in Chinese), 25(3): 946-950, doi: 10.3969/j.issn.1004-2903.2010.03.031. |
| [25] | Wang Z H, Wang J M, Gao Z S, et al. 2013. Pre-stack self-adapting F-X domain coherent noise attenuation technique and application[J]. Progress in Geophys. (in Chinese), 28(5): 2605-2610, doi: 10.6038/pg20130540. |
| [26] | Zhang H, Pan D M, Zhang X Y. 2007. Application of 2-D wavelet transformation in eliminating surface wave interference[J]. Geophysical Prospecting for Petroleum (in Chinese), 46(2): 147-150. |
| [27] | Zhang H, Chen X H. 2013. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese J. Geophys. (in Chinese), 56(5): 1637-1649, doi: 10.6038/cjg20130521. |
| [28] | Zhang J H, Lü N, Tian L Y, et al. 2006. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics (in Chinese), 21(2): 546-553. |
| [29] | Zhang X D, Zhan Y, Ma Y Q. 2007. Approaches of denoise by wavelet transform of different signals[J]. OGP (in Chinese), 42(S1): 118-123. |
| [30] | Zhong B J, Yang G X, Wang H F, et al. 2013. The information-reconstructing and denoising method for data collected with Single-point and high-density[J]. Progress in Geophys. (in Chinese), 28(1): 345-353, doi: 10.6038/pg20130138. |
| [31] | 毕丽飞, 孟宪军, 冯刚,等. 2008. 三维转换波资料处理方法研究及应用[J]. 石油地球物理勘探, 43(S2): 150-154. |
| [32] | 陈文超, 高静怀, 包乾宗. 2009. 基于连续小波变换的自适应面波压制方法[J]. 地球物理学报, 52(11): 2854-2861. |
| [33] | 陈文超, 王伟, 高静怀. 2013. 基于地震信号波形形态差异的面波噪声稀疏优化分离方法[J]. 地球物理学报, 56(8): 2771-2782, doi: 10.6038/cjg20130825. |
| [34] | 韩文功, 于静, 张怀榜,等. 2011. 干扰波调查方法在高密度地震采集中的应用[J]. 石油物探, 50(5): 499-507. |
| [35] | 李国发, 彭苏萍, 高日胜,等. 2005. 转换波地震资料中面波的压制[J]. 石油物探, 44(3): 214-216. |
| [36] | 李雪英, 孙丹, 侯相辉,等. 2011. 基于广义S变换、经验模态分解叠前去噪方法的比较[J]. 地球物理学进展, 26(6): 2039-2045, doi: 10.3969/j.issn.1004-2903.2011.06.019. |
| [37] | 刘春园, 徐胜峰. 2009. 极化滤波在三分量噪声衰减中的应用研究[J]. 地球物理学进展, 24(5): 1814-1823, doi: 10.3969/j.issn.10042903.2009.05.036. |
| [38] | 刘建华, 刘福田, 胥頤. 2006. 三分量地震资料的偏振分析[J]. 地球物理学进展, 21(1): 6-10. |
| [39] | 柳建新, 李杰, 杨俊. 2010. 改进的小波分频重构算法在石油地震勘探中的应用[J]. 地球物理学进展, 25(6): 2009-2014, doi: 10.3969/j.issn.1004-2903.2010.06.016. |
| [40] | 刘洋, 魏修成. 2006. 三维转换波地震资料处理方法[J]. 天然气工业, 26(12): 72-74. |
| [41] | 刘洋, 王典, 刘财,等. 2011. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用[J]. 地球物理学报, 54(2): 358-367, doi: 10.3969/j.issn.0001-5733.2011.02.012. |
| [42] | 刘志鹏, 陈小宏, 李景叶. 2008. 径向道变换压制相干噪声方法研究[J]. 地球物理学进展, 23(4): 1199-1204. |
| [43] | 孟小红, 郭良辉, 张致付,等. 2008. 基于非均匀快速傅里叶变换的 最小二乘反演地震数据重建[J]. 地球物理学报, 51(1): 235-241. |
| [44] | 彭建亮, 彭真明, 张杰,等. 2012. 基于分数域自适应滤波的地震信号去噪方法[J]. 地球物理学进展, 27(4): 1730-1737, doi: 10.6038/j.issn.10042903.2012.04.054. |
| [45] | 沈鸿雁, 李庆春. 2010. 奇异值分解(SVD)实现地震波场分离与去噪新思路[J]. 地球物理学进展, 25(1): 225-230, doi: 10.3969/j.issn.1004-2903.2010.01.030. |
| [46] | 覃天. 2009. 基于小波分频叠前相干噪声压制方法[J]. 地球物理学进展, 24(4): 1426-1430. |
| [47] | 汪铁望, 于相海, 胡浩,等. 2010. 弯曲测线地震资料相干噪声压制[J]. 地球物理学进展, 25(3): 946-950, doi: 10.3969/j.issn.1004-2903.2010.03.031. |
| [48] | 王兆湖, 王建民, 高振山,等. 2013. 叠前自适应F-X域相干噪音衰减技术及应用[J]. 地球物理学进展, 28(5): 2605-2610, doi: 10.6038/pg20130540. |
| [49] | 张华, 潘冬明, 张兴岩. 2007. 二维小波变换在去除面波干扰中的应用[J]. 石油物探, 46(2): 147-150. |
| [50] | 张华, 陈小宏. 2013. 基于jitter采样和曲波变换的三维地震数据重 建[J]. 地球物理学报, 56(5): 1637-1649, doi: 10.6038/cjg20130521. |
| [51] | 张军华, 吕宁, 田连玉,等. 2006. 地震资料去噪方法技术综合评述[J]. 地球物理学进展, 21(2): 546-553. |
| [52] | 张旭东, 詹毅, 马永琴. 2007. 不同信号的小波变换去噪方法[J]. 石油地球物理勘探, 42(增刊): 118-123. |
| [53] | 仲伯军, 杨贵祥, 王海峰,等. 2013. 单点高密度地震资料的信息重构去噪处理方法[J]. 地球物理学进展, 28(1): 345-353, doi: 10.6038/pg20130138. |
 2014, Vol. 29
2014, Vol. 29

