地磁场(徐文耀，2004;白春华等，2008)的研究是地球科学的重要组成部分，借助科学可视化技术(Upson et al., 1989;Nielson and Shriver， 1990)来表达地磁场能帮助研究人员更形象、准确地理解地磁场结构.地磁场的可视化效果优劣在于其能否准确和充分表征场本身的物理特性.最常用的磁场表现方式是磁力线.通过数值积分算法(Shiroyama，1990；李庆杨等，2008)可以实现磁力线的追踪，也可以采用流函数(Kenwright and Mallinson， 1992)的方法来构造磁力线.从地球表面追踪磁力线时，种子点的选择决定了磁力线在空间的疏密分布.目前，国内研究较少涉及磁力线疏密如何准确映射磁感应强度大小的问题，仅黄学良等人在1995年发表了一篇关于工程中电磁场绘制问题研究的论文(黄学良等，1995)，但其疏密约束局限在二维空间里讨论，且没有针对地球表面磁力线种子点分布单独研究.国外学者较早开始进行三维磁力线可视化问题的研究(Yamashita et al., 1981；Shaikh et al., 1988；Ellis and Smith， 1995； Simkin，1995；Cingoski et al., 1996；Noguchi et al., 2004； Noreika and Tarvydas， 2008；Hafner et al., 2010b；Noguchi et al., 2011; Matsutomo et al., 2012；Matsutomo et al., 2013)，日本的 Hideo Yamashita等提出了计算三维空间磁力线疏密的解析方法.但他是采用基于实际数据的统计算法得到种子点数量和位置，而不是基于物理约束来进行磁力线种子点选取.

基于实际数据的统计算法，是根据子平面磁通量占整个主平面磁通量的比例来分配给子平面相应数量的磁力线，然后计算每个子平面的磁通密度中心点，把磁力线移到该子平面内磁通密度高的区域.由

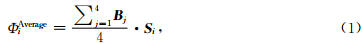
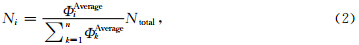
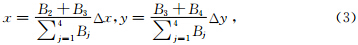
此方法的关键是如何划分子平面.划分后要能够方便地计算出每个子平面上的磁力线数目和起始位置.困难在于无法准确评估一个平面应该划分为多细的子平面才能确定每一条磁力线的最佳起始位置，且最后只能确定磁力线种子点的区域，并不能准确找到每一条磁力线的起始点.这是基于数据的统计算法不可避免要遇到的问题.

这种方法的基础是已经获得的数据，其又受限于所获得的数据.而在模型可视化中，所有点的数据总是可以计算出来的，关键是需要计算哪些点的数据，要对需求进行预判.基于数据的统计方法显示出其劣势.针地磁场模型可视化的特点，本文从基于物理约束的角度出发研究磁力线种子点选取算法，提出了更简单、准确、可行的方法来找寻种子点，包括等磁通量法和等磁通密度衰减法.

空间中某平面的磁通量大小正比于垂直穿过该平面的磁力线数目.为方便研究地磁偶极子场磁力线分布，选取磁力线垂直穿过的磁赤道面入手，得到磁力线在此面上的约束条件；为了能追踪任意纬度的磁力线，需要由磁力线方程反推出其在地球表面的种子点所受约束规则.最后从种子点开始追踪磁力线.

先推导地磁偶极子场磁感应强度 B和磁力线方程.如图 1a，球坐标下，O点是磁偶极子中心，Z轴负向与磁偶极矩 M同向，r 是空间某点到地心距离，θ是磁余纬，φ是磁经度；再看(b)，假设三条磁力线F₁、F₂、F₃在同一磁经度面上，A、B、C分别是F₁、F₂、F₃与地球表面的交点，θ₁、θ₂、θ₃是点A、B、C的磁余纬，r_1，0、r_2，0、r_3，0分别是F₁、F₂、F₃与磁赤道面的交点到偶极子中心(地心)的距离.

图 1

Fig. 1

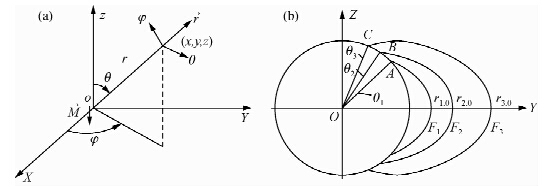图 1 地磁偶极子场(a)及同一磁经度面上磁力线分布(b)示意图 Fig. 1 The geo-magnetic dipole field and the distribution of magnetic flux lines on the same longitudinal plane

偶极子磁场

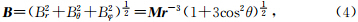
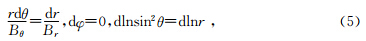
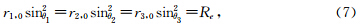
假设两个平面区域内磁场均匀，当磁力线垂直穿过时，若两平面内磁通量相等，则由磁通量的定义Φ=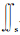 B ·d S，可知磁通密度之比等于面积的反比.如图 2，选择磁赤道面上两小扇形块区域ABED(图 2中红色)和BCFE(图 2中黄色)讨论. r _n，0，r _n+1，0，r _n+2，0分别是磁力线F_n、F_n+1、F_n+2与磁赤道面交点A、B、C到地心的距离.D、E、F分别是扇形块区域另一端上三条磁力线与磁赤道面的交点.

图 2

Fig. 2

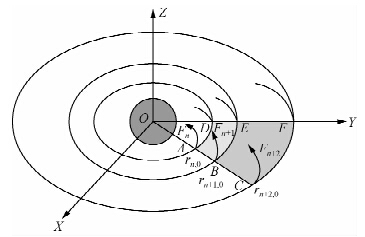图 2 磁赤道面上磁力线分布示意图 Fig. 2 The distribution of magnetic flux lines on the magnetic equatorial plane

由于 B 的大小只与到偶极子中心距离相关，则只要满足点A和B间隔足够小，就可用边界点的磁感应强度来近似区域的磁感应强度.则有

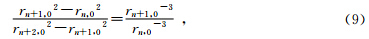
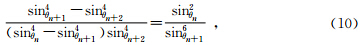
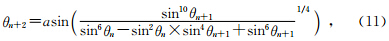
接下来分析算法表征的特性.由式(9)知r_n，0n+1，0，等式(9)右边小于1，令

n+1时式子才能成立，所以磁力线越远离地球中心越稀疏.

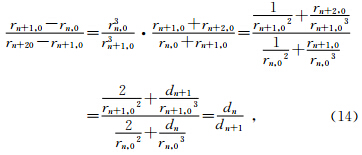
式(9)中令

又有式(12)，所以把r_n，0看成未知数，d_n看成常数，f对r_n，0求导，有

所以面积比值f是随距离r逐渐减小的，即磁力线变稀疏的速度是减小的，知面积法中磁场衰减速度变慢.

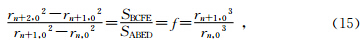
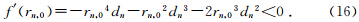
由式(4)，

可知距离地心越远，磁感应强度越小，且强度衰减越慢.

综上，等磁通量法结果理论上与偶极子场的特征相符.

1.2 等磁通密度衰减法 1.2.1 算法推导

不同于等磁通量法，该算法在磁感应强度的等值衰减条件下来表征某处磁感应强度大小.先在磁赤道面上确定初始两磁力线上两个点A、B，磁感应强度 B _A、 B _B和距地心距离 r_A、r_B则确定.绘制第三条磁力线时，第三个点C按以下规则找寻：

即每两条相邻磁力线间的磁感应强度按同样大小变化.算出C点磁感应强度值，进而找到A、B连线上的C点坐标.由公式(4)、(7)和(18)，可以得到磁力线在地球表面的约束：

1.2.2 算法分析

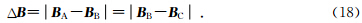
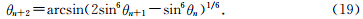
再分析算法表征的特性.式(18)中，代入磁感应强度计算公式(4)，可以得到磁感应强度变化值f与距地球中心距离x的关系(d_n是磁赤道面上点n、点n+1之间的距离)：

所以，若间距d不变，随距离增大Δ B 将变小，衰减减慢；反之，若Δ B 不变，d将变大，磁力线越稀疏.所以该算法得到的磁场性质与由式(17)得到的磁场性质是相符的.

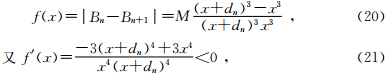
另外，由式(19)知，当θ_n+1比θ_n小很多，不能保证括号里的内容为正时后续计算结果就会出现负无穷(见表 2a结果).从磁力线在磁赤道面上的分布看，两条磁力线间的Δ B 一定，因为磁场值衰减到某个时刻时会出现不够减的情况，所以导致θ_n+2不可解.等磁通密度衰减法只有在初始磁余纬间隔很小时，才可能延迟出现负无穷的情况，但无法避免.

1.3 磁力线追踪系统

按照等磁通量法和等磁通密度衰减法规则选取地球表面种子点，采用经典四阶龙格库塔法实现磁力线追踪.构建地磁偶极子场磁力线三维可视化原型系统，在此系统中实现对磁力线疏密算法的验证.追踪算法核心实现部分如图 3：

图 3

Fig. 3

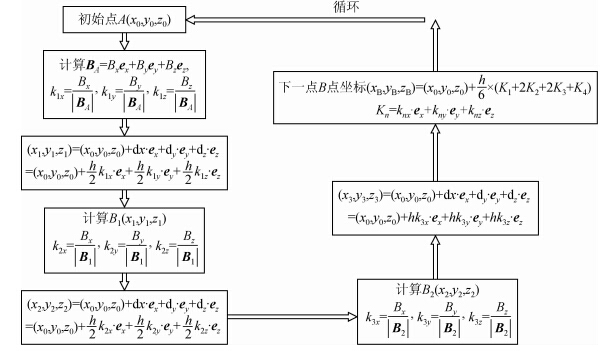图 3 经典四阶龙格库塔法实现磁力线追踪 Fig. 3 The tracing of magnetic flux lines based on the classical fourth order runge-kutta method

2 示例验证

在磁力线可视化系统中磁力线步长h取200000.0 m，种子点的磁经度相同，每条磁力线追踪150个点，绘制10条磁力线.

(1)根据初始两条磁力线种子点磁余纬计算后续磁力线种子点磁余纬，以下分a、b、c、d四种情况，从高、低纬度，不同初始磁余纬间隔方面进行讨论.如表 1.

表 1(Table 1)

表 1 计算的不同种子点磁余纬结果 Table 1 Results of the magnetic colatitudes calculated from different seed points 磁余纬(°) 初始点1 初始点2 点3 点4 点5 点6 点7 点8 点9 点10 等磁通量法 a 47.000 45.000 43.013 41.031 39.048 37.055 35.045 33.011 30.943 28.835 b 47.000 46.000 45.002 44.007 43.012 42.017 41.020 40.021 39.018 38.010 c 62.000 60.000 58.081 56.229 54.429 52.672 50.950 49.254 47.580 45.921 d 62.000 61.000 60.021 59.063 58.121 57.196 56.284 55.385 54.497 53.619

表 1 计算的不同种子点磁余纬结果 Table 1 Results of the magnetic colatitudes calculated from different seed points

由表 1的四种情况的计算结果绘制相应的a、b、c、d四种效果图.红色水平线代表磁赤道面与磁经度面交线.同一经度面上的磁力线图和c条件下的完整三维效果图，见图 4.

图 4

Fig. 4

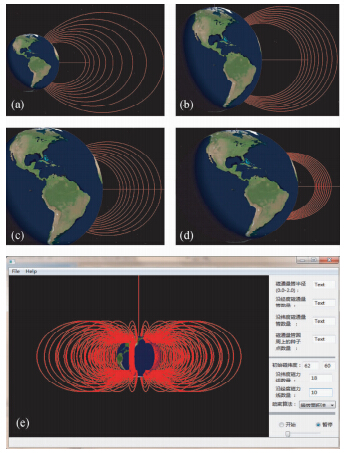图 4 同一磁经度面上等磁通量法的磁力线图和三维效果图 Fig. 4 The magnetic flux lines based on equivalent magnetic flux on the same longitudinal plane and their 3d visualization

(2)等磁通密度衰减法相应结果如下：

由表 2的四种计算结果绘制同一磁经度面上相应的a、b、c、d四种磁力线图及c条件下的完整三维效果图，如图 5.

图 5

Fig. 5

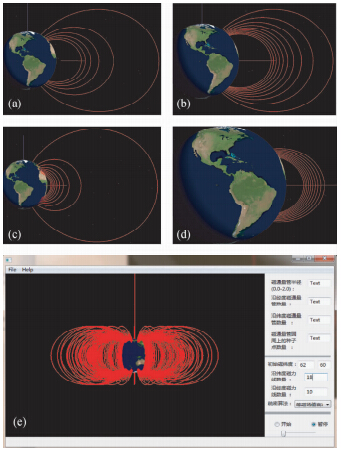图 5 同一磁经度面上等磁通密度衰减法的磁力线图及三维效果图 Fig. 5 The magnetic flux lines based on equivalent reduction of magnetic flux density on the same longitudinal plane and their 3d visualization

(3)表 1、2中种子点间纬度差计算结果如表 3.

表 2(Table 2)

表 2 计算的不同种子点磁余纬结果 Table 2 Results of the magnetic colatitudes calculated from different seed points 磁余纬(°) 初始点1 初始点2 点3 点4 点5 点6 点7 点8 点9 点10 等磁通密度衰减法 a 47.000 45.000 42.672 39.818 35.946 28.964 -1.#IN -1.#IN -1.#IN -1.#IN b 47.000 46.000 44.928 43.770 42.503 41.094 39.492 37.613 35.296 32.158 c 62.000 60.000 57.915 55.707 53.319 50.665 47.600 43.823 38.512 25.486 d 62.000 61.000 59.982 58.944 57.879 56.783 55.649 54.469 53.234 51.932

表 2 计算的不同种子点磁余纬结果 Table 2 Results of the magnetic colatitudes calculated from different seed points

3 讨论分析

从表 1、2、3和效果图可以得出绘制的偶极子场有以下特征：

表 3(Table 3)

表 3 种子点间的磁余纬度差 Table 3 The differences of colatitudes between every two seed points 种子点磁余纬度差(单位：度) 点1-点2 点2-点3 点3-点4 点4-点5 点5-点6 点6-点7 点7-点8 点8-点9 点9-点10 等磁通量法 a 2 1.987 1.982 1.983 1.993 2.01 2.034 2.068 2.108 b 1 0.998 0.995 0.995 0.995 0.997 0.999 1.003 1.008 c 2 1.919 1.852 1.8 1.757 1.722 1.696 1.674 1.659 d 1 0.979 0.958 0.942 0.925 0.912 0.899 0.888 0.878 等磁通密度衰减法 a 2 2.328 2.854 3.872 6.982 -1.#IN -1.#IN -1.#IN -1.#IN b 1 1.072 1.158 1.267 1.409 1.602 1.879 2.317 3.138 c 2 2.085 2.208 2.388 2.654 3.065 3.777 5.311 13.026 d 1 1.018 1.038 1.065 1.096 1.134 1.18 1.235 1.302

表 3 种子点间的磁余纬度差 Table 3 The differences of colatitudes between every two seed points

从表 4知，可视化系统结果图像是和算法理论预测的结果一致的，是符合地磁偶极子场特征的.可视化系统验证了等磁通量法和等磁通密度衰减法的可行性.

表 4(Table 4)

表 4 从表 1、2、3和效果图所得地磁偶极子场特征 Table 4 Characteristics of geo-magnetic dipole field come from tables and pictures 距离r越大 磁赤道面上间距d随距离r的变化 地球表面种子点间距d随纬度变化 初始种子点间距 等磁通量法 磁力线越稀疏，磁感应强度越小 磁力线间距增大速度变慢，磁感应强度衰减变慢 低纬到45度之前，种子点间距逐渐变小45度以后，种子点间距逐渐变大 磁力线间距越大，衰减越快 等磁通密度衰减法 磁力线越稀疏，磁感应强度越小 磁力线间距变大，磁感应强度衰减变慢 低纬到高纬，种子点间距变大

表 4 从表 1、2、3和效果图所得地磁偶极子场特征 Table 4 Characteristics of geo-magnetic dipole field come from tables and pictures

4 结 论

4.1    与传统的基于数据的统计算法不同，本文提出了基于物理约束的更严谨的磁力线种子点选取规则，可以精确找到每一条磁力线的种子点.对于给定数目的磁力线，磁力线的间距也是很容易调节的.采用经典四阶龙格库塔法实现了磁力线追踪.从算法的理论预测到最终效果图都让人比较满意，能较好吻合地磁偶极子场本身的特征.

4.2    然而，两种算法的适应性也有限.毕竟它们的理论基础是偶极子磁场，不能适用于一般的电磁场环境.但它们主要提供了解决问题的新思路：如何从基于物理约束的角度出发研究磁力线种子点选取；三维场在什么情况下如何转化到二维环境下讨论；如何通过特定条件下的磁力线图表征磁场性质.这些思路对于解决一般的电磁场可视化问题比较具有启发性.