2. 哈尔滨工程大学 水声工程学院, 哈尔滨 150001;
3. 海军海洋测绘研究所, 天津 300061
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
3. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
海底底质类型特征是海洋地质调查、海洋工程建设、海底矿产资源开发等领域中重要的海洋环境信息(陶春辉等,2004; Anderson et al., 2008),其调查手段主要包括传统的直接海底取样以及声学、光学、电磁波等间接遥感方式.其中的声学方式称为声学海底分类(Acoustic Seabed Classification,ASC)(Anderson et al., 2007,2008),原理是利用声反射和声散射数据所携带的海底声学特征信息与一定数量的传统取样或光学观察样本,结合适当的分类方法对底质类型进行判别. 该方法具有效率高、取得资料连续等优点,适合大面积、快速的底质探测,这对于海洋科学考察、海洋工程应用等领域都具有重要意义(唐秋华等,2007; 张国堙等,2012). 地貌图像是多波束、侧扫声纳等声学分类系统(acoustic classification systems,ACS)对海底反向散射数据的一种影像化形式,可在此基础上通过基本统计算法、纹理与功率谱分析等多种方法提取分类特征,而且这些特征经常被联合使用以期最大限度地提高分类精度(Brown et al., 2011).目前所采用的分类方法主要有人工神经网络(Marsh and Brown, 2009)、贝叶斯分类器(Simons and Snellen, 2009)、聚类(Preston,2009)、支持向量机(support vector machine,SVM)(郭军等,2012)等.其中的支持向量机是基于结构风险最小化原理的分类器,综合考虑经验风险和置信风险,该分类器具有较强的泛化能力,并在解决小样本、非线性、高维特征数和全局最优解等实际问题中具有独特的优势(邹华胜等,2007; 张长开等,2012),并已成功应用于声学海底分类领域(石丹等,2009; 郭军等,2012). 合成核SVM是近年来在传统单核SVM基础上提出的一种灵活性更强的分类方法(汪洪桥等,2010).该方法通过利用多个核函数,综合不同来源的特征数据进行分类,与单核相比增强了决策函数的可解释性,并已在高光谱分类中展现出了更优的性能(Mountrakis et al., 2011).因此,本文进一步研究基于合成核SVM的多波束海底声图像底质分类方法.为充分研究如何利用合成核SVM提高底质分类精度,结合多波束海底声图像数据分类中经典的三种特征信息(Preston,2009),即图像数据的多阶矩、分位数等基本统计量,基于灰度共生矩阵的纹理特征以及基于功率谱比的Pace谱特征,以此为合成核的构造形成多种数据组合形式,并通过海试数据处理对该方法性能进行讨论.
1 特征提取算法 1.1 图像数据的基本统计描述
多波束海底图像中灰度值的多阶矩以及能描述其统计分布特性的分位数等常常作为最基本的分类特征,而且该特征在解决实际的分类问题中贡献也较为明显(Preston,2009).本文采用图像数据的均值、标准差、偏度、峰度、以及四分位数、内四分极值、极差构成特征向量.
1.2 基于灰度共生矩阵的纹理分析利用基本统计量可以定量描述图像内所有像素灰度值(反向散射强度数据的灰度形式)的统计分布特性,而纹理分析可以补充获取图像内灰度值在平面空间上变化的频率.灰度共生矩阵(grey level co-occurrence matrices,GLCM)是一种建立在二阶统计分析基础上,利用图像中灰度的空间相关特性来描述纹理特征的方法.设图像I中水平、垂直方向分辨单元个数分别为 Nx和Ny,灰度级为Ng,则GLCM是一个Ng×Ng矩阵,其矩阵元素P(i,j)表示为从图像灰度值为i的像元(x,y)出发,统计与其距离为d,方向角度为θ条件下,灰度为j的像元(x+Δx,y+Δy)同时出现的频度,即
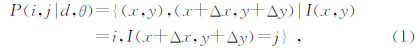
式中,x=1,2…,Nx,y=1,2…,Ny,i,j=1,2,…Ng.本文采用由GLCM矩阵定义的6个代表性较好的特征(Preston,2009; 杨词银等,2005),分别是能量(energy)、对比度(contrast)、相关(correlation)、熵(entropy),均匀性(homogeneity),簇阴影(cluster shade),具体表达式如下
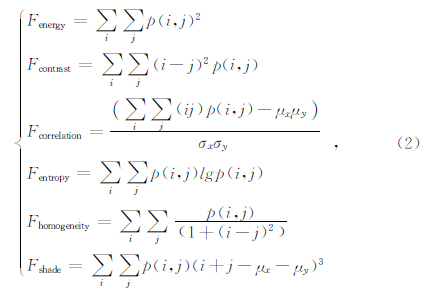
不仅是纹理特征,不同底质图像的功率谱也表现出一些明显的差别.(Pace and Gao, 1988)基于这一特性,针对侧扫声纳接收的海底回波幅度时间序列,利用归一化的对数功率谱得到了3个特征量.文献(Clarke,2004; Ahmed and Demar,2013)又将该方法直接应用到多波束海底声图像数据中.假设样本区域图像由M×N个像素构成,首先计算图像中每行像素序列的功率谱Pi(f),i=1,…,M,并进行平均与归一化处理
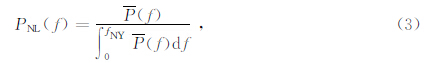
其中,P(f)= 1 M ∑ M 1 Pi(f).由此可以得到Pace谱特征一般表达式
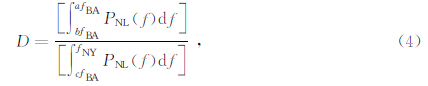
式中,fNY=1/(2Δd),Δd为相邻两像素间距,fBA
SVM分类器最初设计为二类分类,通过寻找最优超平面将不同类型的样本分开.对于非线性可分的训练样本集T= xi,i=1,…,l,xi∈ R n(l、n分别为向量 x 的个数与维数),通过非线性映射Φ将 R n空间的向量映射到Hilbert空间 Η,即Φ(x)∈ Η .而在该特征空间的两个超平面利用求解如下二次规划问题得到

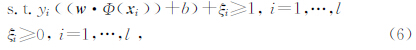
式中,w∈H 为权向量,C为惩罚系数,yi为第i类的类别标号取±1,ξi为松弛变量,· 表示欧几里得范数,而另式中等号成立的样本称为支持向量.引入Lagrange函数来求解上述问题的等效解
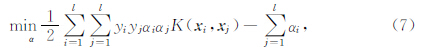
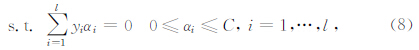
式中,αi为Lagrange乘子,K(x i,x j)=Φ(x i)·Φ(x j)为核函数,在满足Mercer定理的条件下核函数可以有多种形式.而决策函数构造为
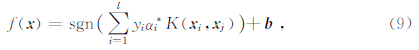
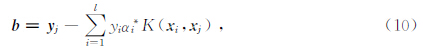
当处理多类问题时,可通过组合多个二类分类器来实现多类分类器的构造,常用方法有一对多(one-versus-rest)、一对一(one-versus-one)等.
2.2 合成核函数的构造根据多核SVM的定理和引理(汪洪桥等,2010; Bekkari et al., 2013),可以将不同基本核函数通过加权加法形式合成新的核函数:

式中μj≥0,∑ M j=1 μj=1,Kj是基本核函数,M是其总个数.在该多核框架下,可以将不同信息源的特征空间利用权系数进行组合构建,这样更能充分利用各基本核特征的映射能力,增强决策函数的可解释性(汪洪桥等,2010).对于权系数的学习,本文采用一种简单且有效的方式(Tanabe et al., 2008)

其中,Aj为仅基本核Kj情况下的分类精度,δ是判别域值,一般不大于所有单核条件下的最小精度.假设由上述特征提取算法得到训练样本i的基本统计特征向量 x Basici∈iNBasic、GLCM特征特征向量 x GLCMi∈iNGLCM,以及Pace谱特征向量 x Pacei∈iNPace,NBasic、NGLCM、NPace分别为该3组特征向量的特征数目.结合上述3个特征向量组定义如下合成核函数:
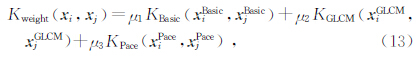
dim(Kweight)=dim(KBasic)=dim(KGLCM)=dim(KPace)=l×l.参数μj在分类时用于调节3个向量组信息的权重,当μj≠0时,表示合成后的特征空间由3个特征向量组组成,任意令其中一个μj为0时,则表示合成特征空间由双基本核组成,这样一共可形成4种合成核组合方式.如图 1所示为合成核构成示意图,对于公式(13)中每个单核核函数,这里选择常用的径向基核函数(radial basis function,RBF)
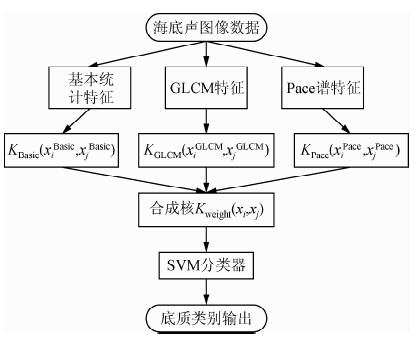 | 图 1 多核函数实现合成核SVM示意图 Fig. 1 Sketch map of composition using multiple kernel |
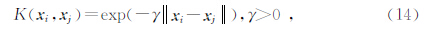
而(14)式中的参数γ和(5)式中的惩罚系数C采用基于交叉验证的网格搜索方法寻找最优值(邓乃扬和田英杰,2009).
3 实验与分析新罕布什尔大学海岸海洋测绘中心(Center for Coastal and Ocean Mapping,University of New Hampshire)提供的shallow survey 2008数据集作为本文实验研究对象.数据集于美国朴茨茅斯外港某处长约1200m,宽约800m的长方形区域采集得到,包括了由多种型号多波束测深系统测量的海底地形数据以及海底反向散射声学数据,并且在该区域进行了摄像系统水下观测与现场地质取样.根据调查结果分析该区域的海底底质类型可分为砂,砾质砂,砂质砾,泥质砂质砾,基岩等5种类型.
本文利用数据集中由Reson公司Seabat 7125多波束测深系统采集的海底反向散射声学数据处理得到海底图像.如图 2所示为5个不同底质类型的海底声图像部分样本,该5个子图均由80×80个像素组成,像素间距为0.4 m,像素值大小为海底反向散射强度数据的灰度显示形式.如图 3、图 4分别为由图 2数据得到的GLCM(d=1,θ=0°)与归一化功率谱的对数显示结果.
 | 图 1 多核函数实现合成核SVM示意图 Fig. 1 Sketch map of composition using multiple kernel |
 | 图 3 由图 2数据得到的GLCM二维显示 Fig. 3 Two-dimensional display of GLCM obtained from image data in Fig. 2 |
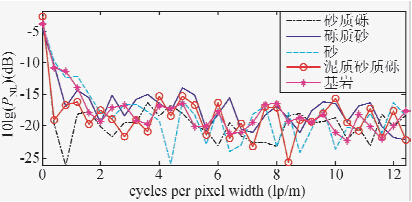 | 图 4 由图 2数据得到的归一化功率谱,并取对数显示 Fig. 4 Logarithm display of normalized power spectrum obtained from image data in Fig. 2 |
在获得图像数据、GLCM以及归一化功率谱这三种信息源的基础上,根据特征提取算法可以分别得到基本统 计量Fbasic,灰度共生矩阵特征FGLCM和Pace谱特征FPace三种特征数据.将其组合成Fbasic、FGLCM、FPace、Fbasic+FGLCM、Fbasic+FPace、FGLCM+FPace、Fbasic+FGLCM+FPace方式进行分类实验,以总体分类精度和Kappa系数为评价指标,采用一对一策略分类,并通过训练样本的交叉验证得到最优参数,(Bekkari et al., 2013)中参数的搜索范围用以10为底,指数项变化步长为1的幂指数形式表示,本文为得到更精细结果,采用以2为底的幂指数形式,即RBF核参数取值范围γ={2-10,2-9,…,210},惩罚系数范围是C={2-10,2-9,…,210}.根据原位采样以及视频观测结果,共获得有海底底质类别标注信息的声图像样本684组,随机抽取其中的一半用于训练学习,另一半用于验证.
用单核SVM对上述7种特征向量或向量组合进行分类实验,分类结果和Kappa系数如表 1所示.从表 1中可以看出,三个特征提取方法中,Fbasic与FGLCM分类能力相对较好;不同特征向量联合使用时,Fbasic+FGLCM两种特征向量的联合后与原来单一特征向量相比精度提高,说明在分类特性上二者具有一定的互补性,FGLCM+FPace的联合效果也同样说明了该现象.而Fbasic与FPace联合使用时,二者的联合分类精度要低于Fbasic自身,这说明FPace对分类决策的干扰作用也较大.
|
|
表 1 单核SVM分类精度 Table 1 Classification Accuracy of Single-Kernel SVM |
表 2为4种特征向量组合采用合成核SVM的分类结果.对比以上两组实验,可以看出所有的合成核分类精度都高于单核SVM.如,Fbasic+FPace的合成核效果与Fbasic+FPace单核形式相比,总体分类精度与Kappa系数提高程度约3%,特别是与Fbasic自身分类精度相比也有所提高,这也说明通过合成核构造,抑制了FPace对整体分类决策的干扰因素.另外,4种合成核组合与单核对比结果可以看出,其提高程度也有所不同,这说明分组方式对于分类结果影响较大.从结果上看Fbasic+FGLCM的组合方式分类性能最好,这里在Fbasic+FGLCM合成核SVM分类训练的基础上得到测量区域的整体分类结果,如图 5与图 6分别为该测区的海底声图像以及分类效果图.
|
|
表 2 合成核SVM分类精度 Table 2 Classification Accuracy of Composite Kernel SVM |
 | 图 5 多波束声纳在研究区域测量的海底反向散射图像 Fig. 5 Seabed backscatter image measured by multibeam sonar in the study area |
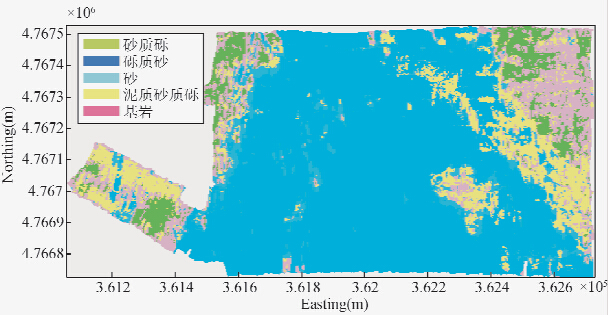 | 图 6 研究区域的底质分类结果 Fig. 6 Results of sediment classification in the study area |
本文引入合成核SVM对多波束海底声图像进行底质分类研究,以shallow survey 2008数据集为例,通过与单核SVM分类精度的对比,验证所提方法的有效性.结果表明:
(1)基于合成核SVM的海底底质分类可得到比传统单核SVM更高的分类精度,验证了合成核SVM在该分类问题中的有效性.
(2)不同种特征向量的融合后,使用单核SVM的分类精度并不一定能比单独一种特征向量获得的分类精度高,如Fbasic+FPace方式,而经合成核SVM处理后可解决此问题.
(3)不同特征信息组合形式对合成核SVM分类性能有较大程度的影响,因此为了获得更好的分类效果,还需要在海底声散射特性的分类机理及其特征提取方法上进行更深入的研究.
致 谢 感谢美国新罕布什尔州新罕布什尔大学海岸海洋测绘中心提供的shallow survey2008数据集支持,这为本文算法的验证提供了有力的帮助.此外,本文研究受到国家自然科学基金科学仪器基础研究专项(41327004),国家自然科学基金青年科学基金项目(41306038),中央高校基本科研业务费专项基金项目(HEUCF140502)以及水声重点实验室基金项目(9140C200105120C2001)的资助,特此感谢.
| [1] | Ahmed K I, Demšar U. 2013. Improving seabed classification from Multi-Beam Echo Sounder (MBES) backscatter data with visual data mining[J]. J. Coast. Conserv., 17(3): 559-577. |
| [2] | Anderson J T, Van Holliday D, Kloser R, et al. 2007. Acoustic seabed classification of marine physical and biological landscapes[R]. ICES Cooperative Research Report No. 286. Copenhagen V, Denmark: International Council for the Exploration of the Sea, 1-7. |
| [3] | Anderson J T, Van Holliday D, Kloser R, et al. 2008. Acoustic seabed classification: current practice and future directions[J]. ICES Journal of Marine Science, 65(6): 1004-1011. |
| [4] | Bekkari A, Yassa M E, Idbraim S. 2013. SVM classification of urban high-resolution imagery using composite kernels and contour information[J]. International Journal of Advanced Computer Science and Applications, 4(7): 126-141. |
| [5] | Brown C J, Todd B J, Kostylev V E, et al. 2011. Image-based classification of multibeam sonar backscatter data for objective surficial sediment mapping of Georges Bank, Canada[J]. Continental Shelf Research, 31(2): S110-S119. |
| [6] | Clarke J E H. 2004. Seafloor characterization using keel-mounted sidescan: proper compensation for radiometric and geometric distortion[C]. //Canadian Hydrographic Conference. Ottawa, Canada: CDROM, 1-18. |
| [7] | Deng N Y, Tian Y J. 2009. Support Vector Machine-Theory, Algorithm and Extension (in Chinese)[M]. Beijing: Chinese Science Press, 81-114. |
| [8] | Guo J, Ma J F. 2012. Support vector machine neural network based on particle swarm optimization in seafloor classification[J]. Geomatics & Spatial Information Technology (in Chinese), 35(12): 66-68. |
| [9] | Marsh I, Brown C. 2009. Neural network classification of multibeam backscatter and bathymetry data from Stanton Bank (Area IV)[J]. Applied Acoustics, 70(10): 1269-1276. |
| [10] | Mountrakis G, Im J, Ogole C. 2011. Support vector machines in remote sensing: A review[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 66(3): 247-259. |
| [11] | Pace N G, Gao H. 1988. Swathe Seabed Classification[J]. IEEE Journal Of Oceanic Engineering, 13(2): 83-90. |
| [12] | Preston J. 2009. Automated acoustic seabed classification of multibeam images of Stanton Banks[J]. Applied Acoustics, 70(10): 1277-1287. |
| [13] | Shi D, Li Q W, Fan X N, et al. 2009. Seafloor sediments classification of side-scan sonar imagery in fast discrete curvelet transform domain[J]. Journal of Applied Sciences-Electronics and Information Engineering (in Chinese), 27(5): 498-501. |
| [14] | Simons D G, Snellen M. 2009. A Bayesian approach to seafloor classification using multi-beam echo-sounder backscatter data[J]. Applied Acoustics, 70(10): 1258-1268. |
| [15] | Tanabe H, Ho T B, Nguyen C H, et al. 2008. Simple but effective methods for combining kernels in computational biology[C].// //Proceedings of IEEE International Conference on Research, Innovation and Vision for the Future. Piscataway, United States: Inst. of Elec. and Elec. Eng. Computer Society, 71-78. |
| [16] | Tang Q H, Liu B H, Chen Y Q, et al. 2007. Application of LVQ neural network combined with the genetic algorithm in acoustic seafloor classification[J]. Chinese J. Geophys. (in Chinese), 50(1): 313-319 |
| [17] | Tao C H, Jin X L, Xu F, et al. 2004. The prospect of seabed classification technology[J]. Donghai Marine Science (in Chinese), 22(3): 28-33. |
| [18] | Wang H Q, Sun F C, Cai Y N, et al. 2010. On multiple kernel learning methods[J]. Acta Automatica Sinica (in Chinese), 36(8): 1037-1049. |
| [19] | Yang C Y, Xu F, Wei J J. 2005. Seafloor sediment classification using a neighborhood gray level co-occurrence matrix[J]. Journal of Harbin Engineering University (in Chinese), 26(5): 5-8. |
| [20] | Zhang C K, Jiang X D, Zhu Z Y, et al. 2012. Attributes selection and reservoir prediction based on support vector machine[J]. OGP (in Chinese), 47(2): 282-285. |
| [21] | Zhang G Y, Tao C H, Li H M, et al. 2012. Seafloor classification in hydrothermal field using multi-beam sonar[J]. Marine Geology Frontiers (in Chinese), 28(7): 59-65. |
| [22] | Zou H S, Ning S N, Yang F, et al. 2007. Application of support vector machine to forecasting and calculating reservoir thickness[J]. Progress in Geophysics (in Chinese), 22(5): 1597-1601. |
| [23] | 邓乃扬, 田英杰. 2009. 支持向量机—理论、算法与拓展[M]. 北京: 科学出版社, 81-114. |
| [24] | 郭军, 马金凤. 2012. 基于粒子群优化算法的SVM神经网络在海底底质分类中的应用[J]. 测绘与空间地理信息, 35(12): 66-68. |
| [25] | 石丹, 李庆武, 范新南,等. 2009. 曲波变换域侧扫声纳图像海底底质分类[J]. 应用科学学报, 27(5): 498-501. |
| [26] | 唐秋华, 刘保华, 陈永奇,等. 2007. 结合遗传算法的LVQ神经网络在声学底质分类中的应用[J]. 地球物理学报, 50(1): 313-319. |
| [27] | 陶春辉, 金翔龙, 许枫,等. 2004. 海底声学底质分类技术的研究现状与前景[J]. 东海海洋, 22(3): 28-33. |
| [28] | 汪洪桥, 孙富春, 蔡艳宁,等. 2010. 多核学习方法[J]. 自动化学报, 36(8): 1037-1049. |
| [29] | 杨词银, 许枫, 魏建江. 2005. 基于邻域灰阶共生矩阵的海底沉积物分类[J]. 哈尔滨工程大学学报, 26(5): 5-8. |
| [30] | 张长开, 姜秀娣, 朱振宇,等. 2012. 基于支持向量机的属性优选和储层预测[J]. 石油地球物理勘探, 47(2): 282-285. |
| [31] | 张国堙, 陶春辉, 李怀明,等. 2012. 多波束声参数在海底热液区底质分类中的应用[J]. 海洋地质前沿, 28(7): 59-65. |
| [32] | 邹华胜, 宁书年, 杨峰,等. 2007. 支持向量机在储层厚度预测和计算中的应用[J]. 地球物理学进展, 22(5): 1597-1601. |
 2014, Vol. 29
2014, Vol. 29


