地球探测技术的进步离不开高端的探测装备(刘光鼎，2013；底青云等，2013)，地震信号采集系统需要大量的高品质传感器来实现高精度地震勘探.然而高精度伴随着高能耗、高成本，如何在二者之间实现相对平衡，尽可能地在满足采集需求的同时延长仪器工作时间、减少系统功耗对于地震勘探的研究具有重大意义(游庆瑜，2003；孔阳，2011；郝天姚和游庆瑜，2011).MEMS数字检波器有机结合了微电子、精密机械、生化和信息处理等高新技术(Dong et al. 2011;Khoshnoud and de Silva，2012; Panas et al. 2012)；同时MEMS数字检波器具有优良的机械电气性能和微型化、高度集成化等特点，这使其能够胜任高精度勘探任务，成为地震数字检波器的发展趋势.

MEMS数字检波器信号读出电路的设计是核心技术之一，其功耗主要由其中的抽取滤波器电路决定.本文主要对抽取滤波器中前端SINC滤波器进行了优化设计和FPGA高效实现.

检波器主要由MEMS敏感器件、Sigma-Delta调制电路、和抽取滤波器3部分组成.基于借助于过采样和噪声整形技术、Sigma-Delta调制数字力反馈结构和高精度闭环反馈与控制(de la Rosa，2011; Kutz et al., 2011; Naqvi et al., 2011)，MEMS数字检波器可以满足高灵敏度、大动态范围的设计要求，并且其同时具有高精度的模/数(A/D)转换(Beeby et al., 2004).检波器结构如图 1所示：

图 1

Fig. 1

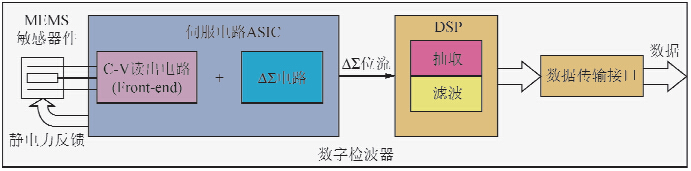图 1 MEMS数字检波器结构 Fig. 1 Architecture of MEMS digital geophone

其中敏感器件结构如图 2所示，器件内部质量块非常轻，而弹性系数较大，从而能够产生非常高的共振频率，质量块的正面和反面，底面和顶面内侧的一小块，涂上金属，形成两个电容.这两个电容可以感知极板间微小距离的变化，从而将微弱震动转化为电信号；Sigma-Delta调制部分通过过采样技术和噪声整形技术，将电信号转换为高速率的1bit数据流，实现模拟信号向数字信号的转换；抽取滤波器将高速率的1bit数据流转换为低速的24bit数据流，实现噪声压制和高精度数据的获取.

图 2

Fig. 2

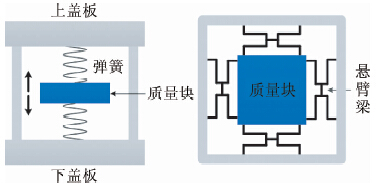图 2 敏感器件内部结构图 Fig. 2 Internal structure of sensitive device

抽取滤波器前端给定的5阶调制解调电路及其输出信号功率谱如图 3(Liang et al., 2012)所示.

图 3

Fig. 3

图 3 五阶Sigma-Delta调制解调结构及其输出数据流的频率谱(a)五阶Sigma-Delta调制解调电路;(b)Sigma-Delta 调制器输出功率谱. Fig. 3 Fifth-order Sigma-Delta structure and the spectrum of the output data(a)fifth-order sigma-delta circuit;(b)Output power spectrum of sigma-delta modulator.

Sigma-Delta ADC的精度主要由调制部分决定，而硬件和功耗则主要由数字抽取滤波器决定.针对前端调制部分输出信号的特点，数字抽取滤波器要完成3个任务：(1)Sigma-Delta调制的任务是噪音和信号分离，抽取滤波的任务是去除信号带外的噪音；(2)Sigma-Delta调制输出的采样率很高，因为它把噪音推到高频，当高频噪音被滤掉后，可以降低采样率，以方便后面的传输，存数，以及数字处理；(3)防止混叠.实际信号时间上是有限的，因此不是带限的，如果降低采样率，则需要防混叠滤波器来防止不同频段信号相互影响.

对于地震信号来说，绝大多数有用的能量聚集在低频段，因此需要数字滤波器是低通的以保证低频部分的能量不损失；其次，还要求地震信号的特性在经过滤波器后不会被改变，这就需要通带波纹足够小；最后，随着对地震勘探要求的提高，为了实现高精度滤波，阻带的衰减必须达到一定的要求.因此，MEMS地震数字检波器对抽取滤波器的要求可以概括为：低通、通带内波纹小、阻带衰减大.其对抽取滤波器的具体要求如下：(1)将Sigma-Delta调制器输出的128 kHz的1 bit数据流进行抽取滤波后输出1 kHz的24 bit数据，即抽取倍数为128；(2)通带波纹小于+/-0.01 dB；(3)-3 dB通带宽度：0~0.4289 Fs;(4)阻带衰减大于130 dB.

抽取滤波器一般包含以下3部分：滤波器前端为SINC滤波器，中间主要是针对SINC做出的补偿滤波器，最后一级为等波纹FIR滤波器(www.curris.com，2008).因为sigma-delta调制器输出的高速率(过采样)1bit数据流直接输入抽取滤波器，所以滤波器运行频率较高，其功耗受到广泛关注，使用合适的结构实现滤波器是一个重要问题(Ignjatovic，2012).抽取滤波器结构如图 4所示，从图中可以看到，SINC滤波器位于抽取滤波器最前端，这是因为(1)算法相对简单;(2)没有系数截断误差;(3)零点位于混叠频点，比同阶滤波器抗混叠效果要好.但是SINC滤波器的运行速度是抽取滤波器中最高的，对其进行优化实现会让系统功耗大为降低.本文主要对SINC滤波器进行了优化设计，并对其进行了FPGA高效实现.

图 4

Fig. 4

图 4 数字抽取滤波器实现架构 Fig. 4 Implementation architecture of digital decimation filter

SINC滤波器本质为滑动平均滤波器，对于每一个输出，仅需要M个加法，是最简单的滤波器.其Z域的传递函数为

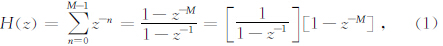
其中M为输入相加的个数，公式前一项表示积分器，后一项为M个延迟的差分器，因此这种实现形式被称为Cascaded Integrator-Comb(CIC).在线性时不变系统中，可以对两项重新排序，如果将k个滤波器级联，积分项放在前面，系统有极点，需要增加字长，以保持稳定，需要的位数是W₀+klog₂M，其中W₀代表输入位宽，k代表及级联个数.

将z=e^jω代入公式1，得到SINC滤波器的频率响应为

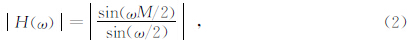
其中f为归一化频率，ω为归一化角度频率，M为抽取数，若在滤波后对数据进行抽取，会发生频谱混叠，所有零点附近的频谱都会混叠进入基带，如图 5所示：

图 5

Fig. 5

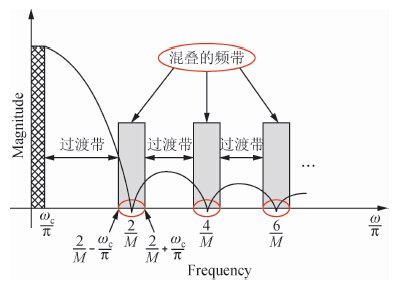图 5 SINC滤波器频率响应 Fig. 5 SINC filter frequency response

因其频谱为SINC函数，故也被称为SINC滤波器.1级SINC滤波器旁瓣较大，多级SINC具有更好的去噪功能，K级SINC的传递函数为

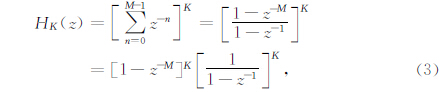
幅频响应可以表示为

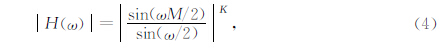
通过对抽取滤波器各级指标进行分解，本文所需要设计的SINC滤波器指标如下：通带截止频率400 Hz；采样率128 kHz；抽取系数16；阻止频带的衰减达到130 dB.通过仿真测试发现：单级实现时，M=16，K=6时，第一个零点位于8 kHz，第一个混叠频点为(8000-400)Hz，其衰减达到150 db，第二个混叠频点为(16000-400)Hz，其衰减达到180 dB，而且混叠频点衰减依次逐级递减，仿真结果如图 6所示：

图 6

Fig. 6

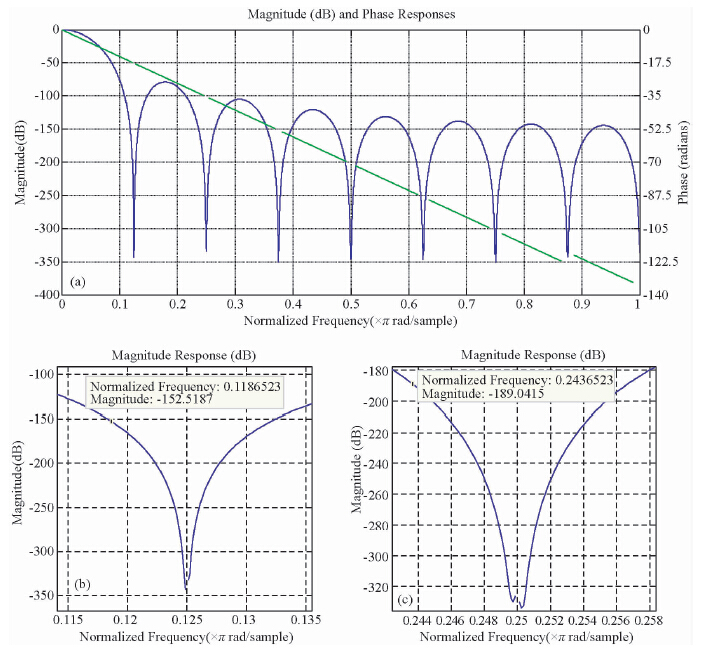图 6 SINC滤波器单级实现幅频相频特性曲线与混叠点分析(a)SINC单级实现时频率与相位响应;(b)第一个混频点;(c)第二个混叠点. Fig. 6 Phase-frequency amplitude-frequency characteristic and aliasing point analysis of single-stage SINC filter(a)Frequency and phase response of singal stage SINC filter; (b)the first frequency aliasing point;(c)the second frequency aliasing point.

抽取滤波器主要考虑功耗的大小，为避免长字节在高采样率下运行，采用2级级联方式实现以减少功耗.因为M=M1·M2，M1不宜过于小，这样后级电路才会工作在低采样率下，从而减少功耗.通过仿真发现：M1=8，K1=5，M2=2，K1=6，时候频率响应曲线与单级时基本重合，满足设计要求，仿真结果如图 7所示.

图 7

Fig. 7

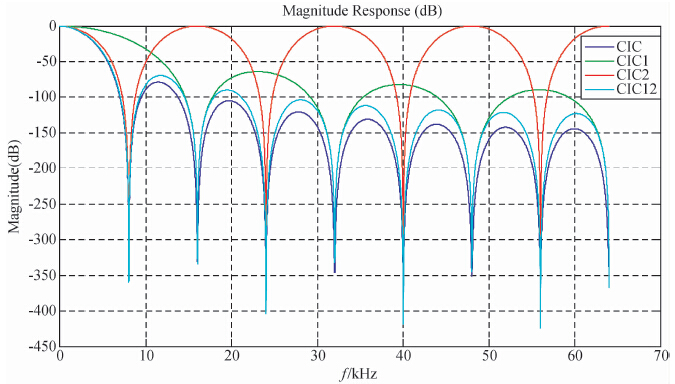图 7 SINC滤波器单级与多级实现的幅频率响应对比 Fig. 7 Amplitude frequency response contrast between singal-stage and multi-stagezhijian

对于高倍数抽取的SINC滤波器Hogenauer提出了一个非常高效的实现结构：“级联积分梳妆滤波器”(CIC，Cascade Integrator Comb)(Hogenauer，1981).两个级联的CIC滤波器数学表达式如下：

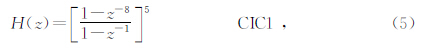
通过对式5进行分析，发现CIC1抽取倍数相对较大，可以直接采用Hogenauer结构以节省资源，如图 8所示.需要注意的是里输入的1 bit数据流需要包装为2 bit的符号数，所以数据位宽应该设置为B_out=2+5log₂⁸=17 bit.

图 8

Fig. 8

图 8 5级8抽取CIC1滤波器结构 Fig. 8 5 stage CIC1 filter structure with 8 times decimation

而对于CIC2抽取倍数为2，而阶数相对较高，不适于采用Hogenauer结构.下面对CIC2进行了专门的优化设计：首先对表达式进行展开，将其表达为非递归形式，然后利用多相分解技术(Aboushady et al., 2000; Al-Haj，2005;Latha and Kumar， 2012)，对其进行处理(式7)，其硬件实现方式如图 9所示：

图 9

Fig. 9

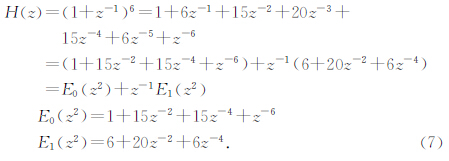
图 9 CIC2多相分解实现方式 Fig. 9 polyphase decomposition implementation of CIC2

然后从以下两点对E₀进行硬件优化实现：(1)将乘法器改为移位器和加法器；(2)利用系数的对称性进行单路复用，优化过程如图 10所示.

图 10

Fig. 10

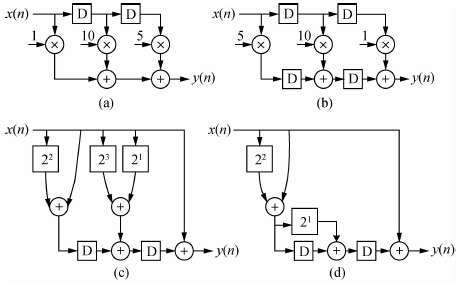图 10 E0硬件电路优化示意 Fig. 10 Hardware schematic circuit optimization of E0

通过上述优化，只需要3个D触发器和一次移位操作就能实现E₀，同样方式优化E₁最终可以得到CIC2滤波器的优化硬件架构，如图 11所示：

图 11

Fig. 11

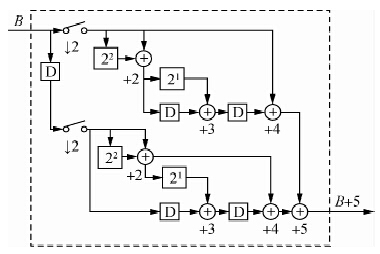图 11 CIC2滤波器的优化结构 Fig. 11 Optimization of CIC2 filter structure

最后对所有硬件电路利用Verilog进行FPGA编程实现.优化前后功耗对比如表 1所示，输入数据位数为17.从表中可以看出优化后将功耗较大的乘法运算转化为基本不产生功耗的移位运算，同时运算频率可以降低2倍，从而较大程度的较少了系统功耗.

表 1(Table 1)

表 1 CIC2优化前后功耗估计对比 Table 1 Power estimation comparison of CIC2 before and after optimization 运行频率 乘法运算 个数/次 加法运算 个数/次 移位运算 个数/次 优化前 16 kHz 5 6 0 优化后 8 kHz 0 8 4

表 1 CIC2优化前后功耗估计对比 Table 1 Power estimation comparison of CIC2 before and after optimization

对于CIC1由其数学表达式有

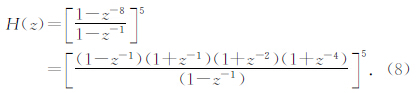
所以其每一级滤波器系数为[1，1，1，1，1，1，1，1]，5级就是5组[1，1，1，1，1，1，1，1]卷积的结果如表 2所示：

表 2(Table 2)

表 2 CIC1等效滤波器系数 Table 2 CIC1 equivalence filter coefficients Filter Type System Function Filter Coefficients SINC1 5 th order decimate by 8 36 coefficients H(z)=[(1-z-8)/(1-z-1)]5 h0=1 h1=5 h2=15 h3=35 h4=70 h5=126 h6=210 h7=330 h8=490 h9=690 h10=926 h11=1190 h12=1470 h13=1750 h14=2010 h15=2226 h16=2380 h17=2460 h18=2460 h19=2380 h20=2226 h21=2010 h22=1750 h23=1470 h24=1190 h25=926 h26=690 h27=490 h28=330 h29=210 h30=126 h31=70 h32=35 h33=15 h34=5 h35=1

表 2 CIC1等效滤波器系数 Table 2 CIC1 equivalence filter coefficients

如果输入端一直为高电平，输出相当于[1，1，1，1…]与滤波器系数的卷积再对其进行8倍数抽取，则CIC1输出的时间序列为：[0，792，11544，28680，32712，32768，32768，32768，…].同理，得到CIC2等效滤波器系数如表 3所示：

表 3(Table 3)

表 3 CIC2等效滤波器系数 Table 3 CIC2 equivalence filter coefficients SINC2(Stage 4) 6 th order decimate by 2 7 coefficients H(z)=[(1-z-2)/(1-z-1)]6 h0=1 h1=6 h2=15 h3=20 h4=15 h5=6 h6=1

表 3 CIC2等效滤波器系数 Table 3 CIC2 equivalence filter coefficients

将CIC1、CIC2级联，则级联后滤波器CIC1的输出为CIC2的输入.同理，两个滤波器级联后得到的滤波器CIC12的输出结果应该为

Y_out=[16296，393792，1471568，2050560，2097096，2097152，…].

本文利用ModleSim软件对FPGA程序进行验证，结果(图 12)表明实验值与理论值一致.

图 12

Fig. 12

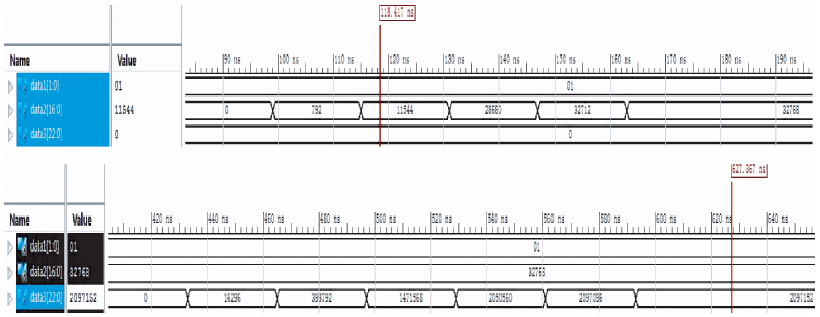图 12 CIC滤波器ModelSim仿真结果(a)输入端一直为1时，第一级CIC滤波器输出;(b)输入端一直为1时，两级CIC级联输出. Fig. 12 ModelSim simulation results of CIC filter(a)Output of first stage CIC filter when inputs is 1; (b)Output of cascaded CIC filter when inputs is 1.

本文针对MEMS数字检波器数字信号处理(DSP)部分中的SINC抽取滤波器进行了研究，经分析采用了多级SINC滤波器，并对其进行了FGPA高效实现，结果满足其高性能指标、并在一定程度上减少了功耗.研究表明：(1)当SINC滤波器的抽取数较大采用CIC结构能够有效减少资源消耗；当SINC滤波器抽取数较小时采用多相分解结构能够较大程度减少功耗；(2)将乘法转化为移位加算法，并通过移位器复用能够有效减少功耗.