2. 中国地质大学工程技术学院, 北京 10083
2. School of Engineering and Technology, China University of Geosciences in Beijing, Beijing 100083, China
研究应力波在岩石中的衰减规律时,用粘弹性介质模型描述岩石比用弹性介质模型更接近于实际情况,应力波的衰减现象能够为岩性、物性及岩石饱和度等研究提供信息(高静怀等,2012).为此,人们提出了许多的数学模型,如Maxwell模型、Kelvin模型、三参量固体模型、Burgers模型等.如何准确测定粘性系数是应用这些模型的关键问题之一.
应力波在介质的传播过程中(刘希强等,2009),受波阵面几何扩散和衰减作用,造成振幅逐渐减小.引起振幅衰减的原因主要有两个方面,一是介质的非弹性作用将机械能变成热能,并引起应力波传播方向与衰减不一致(郝召兵等,2009),称为固有衰减;二是沿射线传播的应力波在介质内部小的非均匀体上发生散射,称为散射衰减.品质因子是度量应力波能量衰减的主要参数(刘财等,2007),能够综合反映介质非均匀性和非弹性引起应力波振幅衰减.对于完整岩石来说,散射引起的衰减可以忽略,主要是由介质的黏性引起振幅衰减,可以采用黏性系数描述应力波能量耗散参数(李灿苹等,2005).目前有关介质衰减参数的测试主要分成两大类:实验室测试和野外测试.(邓科涛等,2002)利用三角波周期加载的方法室内测试了Maxwell模型的粘性系数,(李魁彬等,2007)从Kelvin模型和Euler-bernoulli梁理论出发,利用弹性-粘弹性相应原理和弹性材料动力学理论得出粘弹性梁的动力学方程,提出了黏性系数的室内测试方法.这些室内测试方法主要是利用悬臂梁的振动实验测定粘性系数,由于实验室的测试样品尺寸较小,而且物质离开了原生地和原生条件,这些使实验室结果的推广和应用受到一定的限制(徐平等,2006).为此本文提出现场测试岩石黏性系数的方法.本文把岩石抽象为Kelvin粘弹性体,运用波动方程和复数理论,建立应力波振幅随时间的衰减系数与岩石力学参数的关系,现场试验研究了岩石粘性系数的测试方法.
1 应力波振幅随时间的衰减模型把岩石抽象为均匀Kelvin粘弹性体,设应力波向x方向传播,讨论应力波振幅随时间的衰减规律.岩石中P波的波动方程(牛滨华和孙春岩,2007):
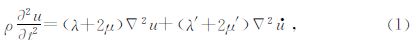
现讨论岩石中某一质点的振幅随时间的衰减系数与岩石的力学参数的关系.设质点与震源的距离为x,以谐波解试之


式(3)是一个复数关系.如果k是实波数,则ω1必为复数,令:

式(4)代入式(3),由复数的实部和虚部分别相等得:
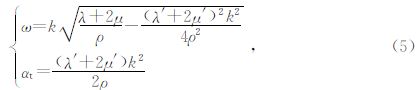

文献(牛滨华和孙春岩,2007)给出了k的计算表达式为
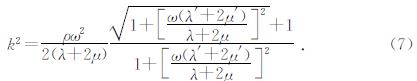
将岩石抽象为Kelvin粘弹性体,其复数弹性模量Ek:


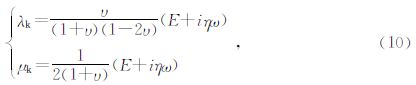
对于弹性介质和粘弹性介质,尽管在理论和方法存在差异,但是两种介质之间也存在显著的关联性和对应性,弹性模量满足对应规则(牛滨华和孙春岩,2007),即:

由式(10)和式(11)可得:
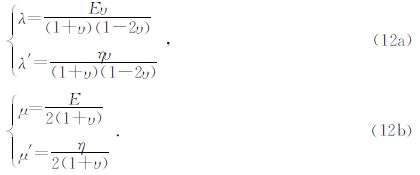
由式(12)可以计算岩石的弹性拉梅常数和粘性拉梅常数.把式(7)和式(12)代入式(5)的第二式便可以得到岩石中应力波振幅随时间的衰减系数.
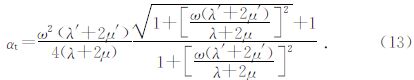
式(13)反映振幅随时间的衰减系数与岩石的力学参数的关系.
式(12)代入式(13)得
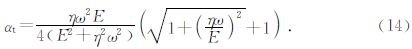
式(14)给出应力波振幅随随时间的衰减系数与岩石力学参数的关系.
2 现场试验及粘性系数的计算 2.1 现场试验方案试验选择在德兴铜矿露天采场,在试验区域进行岩石取样,进行了四组室内试验,测试得到岩石试样的物理力学参数如表 1所示.通过取平均值的方法确定试验区岩石的弹性模量为24.06 GPa,密度为2543 kg/m3,泊松比为0.17.
|
|
表 1 岩样物理力学参数 Table 1 Physical and mechanics parameter of rock specimen |
岩石粘性系数测试现场如图 1所示,选择表面平整且完整性好的岩石,用石膏粉将5个电荷加速度传感器粘结在岩石上,并使各传感器的指向一致,5个传感器与震源的距离分别为0.6 m、0.9 m、1.5 m、2.7 m和4.1 m.传感器参数为:电荷灵敏度10.427~14.091 pC/ms-2,频响范围0.2~5 kHz,谐振频率15 kHz.用人工敲击产生震动信号,震动信号经信号调理仪进行滤波处理后再采集,信号调理仪的参数设置为低通3 kHz,采样率为12 kHz.
 | 图 1 岩石粘性系数的测试现场 Fig. 1 Arrangement diagram of field test of rock viscosity coefficient |
岩石粘性系数的计算步骤:(1)采用快速傅里叶变换进行频谱分析,找出特征频率;(2)根据第1特征频率的有效带宽进行带通滤波,得到第1特征频率对应的特征波形;(3)假设特征波形振幅随时间按负指数衰减,采用负指数拟合特征波形振幅随时间的变化趋势,求出振幅随时间的衰减系数;(4)把5个测点的衰减系数、第1特征频率和岩石的弹性模量代入式(14)计算得到岩石的粘性系数,如表 2所示,进一步计算得到粘性系数的平均值为23.7 MPa·s.
|
|
表 2 第1特征频率、时间衰减系数和粘性系数 Table 2 The first characteristic frequency and time attenuation coefficient and viscosity coefficient |
图 2a为测点3的实测波形,对实测波形进行傅里叶变换,得到测点3的频谱曲线,如图 4所示.从图 4可以看出,测点3的第一特征频率为498 Hz.根据测点3的频谱曲线,确定第一特征频率的有效带宽为460~520 Hz,以有效带宽进行带通滤波得到测点3的特征波形,如图 2b所示.从测点3的特征波形可以看出,经过带通滤波后,波形发生非常大的变化,相对于实测波形,特征波形的振幅有较长的上升时间(起跳至最大振幅的时差).在特征波形振幅下降时间段,采用负指数拟合振幅和时间的关系,得到衰减系数αt.
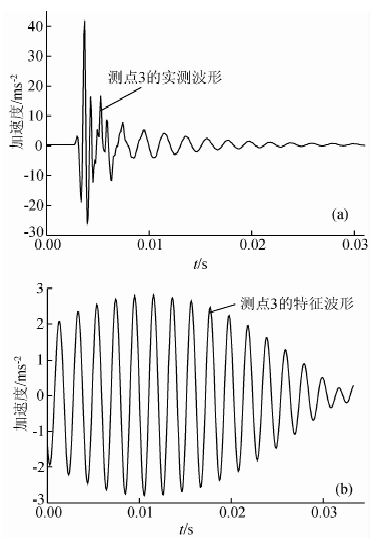 | 图 2 测点3的实测波形和特征波形 Fig. 2 Characteristic wave shape and measured wave shape of measure point 3 |
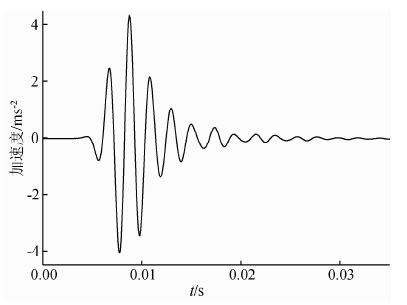 | 图 3 测点4的实测波形 Fig. 3 measured wave shape of measure point 4 |
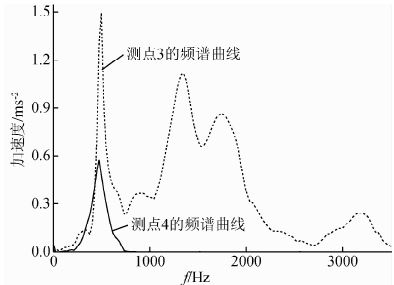 | 图 4 测点3和测点4的频谱曲线 Fig. 4 Frequency spectrum curve of measure point 3 and 4 |
分析5个测点的振动波形发现,测点1、测点2和测点3的波形比较接近,这三个测点与测点4和测点5的波形具有明显变化,而测点4和测点5的波形比较接近.这应该是由震源距离介质的黏性引起的,测点3与震源距离为1.5 m,测点4与震源距离为2.7 m,冲击载荷作用下,岩石产生一个冲击响应,响应具有丰富的频谱分布,经过一段传播距离后,高频成分发生严重衰减,因而波形发生明显变化.图 3为测点4 的实测波形,比较测点3的实测波形,可以发现:相对于测点3,测点4的实测波形具有频率相对单一和主频减小的特点.图 4为测点3和测点4实测波形的频谱曲线,从图中可以看出,应力波从测点3传播至测点4,高频成分完全被衰减了,该现象与高强的理论研究结果完全一致.(高强和林家浩,2005)在频率和波数域中将应力波控制方程化为常微分方程,研究三维黏弹性介质应力波的传播规律,研究结果表明,在载荷作用近区会产生高频谐波成分,且高频谐波成分衰减非常快.有以上分析得出:岩石对冲击载荷会产生 频率非常丰富的谐波成分,其中部分低频谐波在岩石中传播,本文提出基于特征波形振幅随时间衰减系数计算黏性系数的方法,应该根据应力波传播过程中频率的变化来确定滤波范围.
2.3 基于振幅随传播距离的衰减系数计算岩石粘性系数应力波在Kelvin粘弹性体的传播过程中,受到介质的黏性作用,应力波振幅随传播距离发生衰减,文献(孙成禹,2007)给出了平面波衰减系数 αs的计算公式.
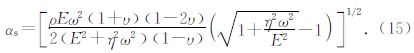
试验产生的应力波可以近似为球面波,在计算应力波振幅衰减时,应考虑波阵面扩散引起的振幅变化.本文采用球面波传播理论修正各测点振幅,得到测点振幅随传播距离的衰减趋势,如图 5所示,采用负指数拟合得到衰减系数αs=0.036.应力波在黏弹性体的传播过程中,应力波主频发生变化,如表 2所示,随传播距离增加,主频逐渐减小,因此各测点主频不相同.本文采用测点主频的平均值542 Hz代入式(15)计算,将表 1的参数和衰减系数αs=0.036代入式(15),计算得到黏性系数为21.8 MPa·s.由αt确定的黏性系数为23.7 MPa·s,由αs确定的黏性系数为21.8 MPa·s,两者的误差为8.7%,误差小于10%.基于应力波振幅随传播距离的衰减系数分析介质的黏性,该方法为相对成熟和广为接受的方法,由此认为:本文提出的基于测点特征波形振幅随时间衰减系数测试岩石黏性的方法是可行的.
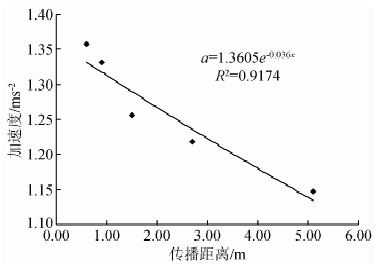 | 图 5 测点振幅随传播距离的衰减趋势 Fig. 5 Attenuation tendency of amplitude of measure point with propagation distance |
本文把岩石抽象为Kelvin粘弹性体,运用波动方程建立应力波振幅随时间的衰减系数与岩石力学参数的关系.提出了基于测点特征波形振幅随时间的衰减系数的岩石粘性系数现场测试方法,合理确定特征频率是该方法的关键工作.
现场试验研究表明,岩石对冲击载荷产生丰富的频谱响应,部分高频谐波分量经过一段传播距离(本文试验发现传播距离小于3m)后完全衰减了,因此需要分析应力波在岩石中传播时频谱变化规律,在此基础上确定特征频率和带通滤波范围.本文是基于应力波在岩石中传播规律提出黏性系数测试方法,应避免将岩石对冲击载荷的高频响应计为特征频率,有效措施是控制测点与冲击载荷作用点间的距离,但合理距离的确定方法有待进一步研究.
| [1] | Deng K T, Wu X. 2002. Text of several material function of the viscoelastic material[J]. Structure & Environment Engineering (in Chinese), 29(3): 58-63. |
| [2] | Gao J H, He Y Y, Ma Y C. 2012. Comparison of the Rayleigh wave in elastic and viscoelastic media[J]. Chinese J. Geophys. (in Chinese), 55(1): 207-218. |
| [3] | Gao Q, Lin J H. 2005. Stationary Random waves propagation in 3D viscoelastic stratified solid[J]. Applied Mathematics and Mechanics (in Chinese), 26(6): 723-733. |
| [4] | Hao Z B, Qin J X, Wu X Y. 2009. Overview of Research on the Seismic Wave Quality Factor(Q)[J]. Progress in Geophys. (in Chinese), 24(2): 375-381. |
| [5] | Li C P, Liu X W, Wang X C, et al. 2005. Seismic wave scattering theory, scattering characteristics and its applications[J]. Progress in Exploration Geophysics (in Chinese), 28(2): 81-89. |
| [6] | Li K B, Wang A W, Hu M Y, et al. 2007. An experimental technique of determining material parameter of viscoelastic Kelvin model[J]. Journal of Naval University of Engineering (in Chinese), 19(6): 26-29. |
| [7] | Liu C, Guo Z Q, Yang B J, et al. 2007. Analysis of reflection and transmission problems of waves in viscoelastic anisotropic media[J]. Chinese J. Geophys. (in Chinese), 50(4): 1216-1224. |
| [8] | Liu Xi Q, Shi Y Y, Qu J H, et al. 2009. Discussion on coda wave measurement methods for quality factor[J]. Earthquake Research in China (in Chinese), 25(1): 11-23. |
| [9] | Niu B H, Sun C Y. 2007. Half-space homogeneous isotropic viscoelastic medium and seismic wave propagation (in Chinese) [M]. Beijing: Geological publishing house. |
| [10] | Sun C Y. 2007. Theory and methods of seismic wave (in Chinese) [M]. Dongying: China University of Petroleum Press. |
| [11] | Xu P, Wang B S, Zhang W, et al. 2006. Estimating seismic attenuation using cross correlation function[J]. Chinese Journal of Geophysics (in Chinese), 49(6): 1738-1744. |
| [12] | 邓科涛, 吴晓. 2002. 粘弹性材料的几个材料函数的测定[J]. 强度与环境, 29(3): 58-63. |
| [13] | 高静怀, 何洋洋, 马逸尘. 2012. 黏弹性与弹性介质中Rayleigh面波特性对比研究[J]. 地球物理学报, 55(1): 207-218. |
| [14] | 高强, 林家浩. 2005. 三维粘弹性分层介质中平稳随机波的传播[J]. 应用数学和力学, 26(6): 723-733. |
| [15] | 郝召兵, 秦静欣, 伍向阳. 2009. 地震波品质因子Q研究进展综述[J]. 地球物理学进展, 24(2): 375-381. |
| [16] | 李灿苹, 刘学伟, 王祥春,等. 2005. 地震波的散射理论和散射特征及其应用[J]. 勘探地球物理进展, 28(2): 81-89. |
| [17] | 李魁彬, 王安稳, 胡明勇,等. 2007. 确定Kelvin模型粘弹性材料参数的一种实验方法[J]. 海军工程大学学报, 19(6): 26-29. |
| [18] | 刘财, 郭智奇, 杨宝俊,等. 2007. 黏弹各向异性介质中波的反射与透射问题分析[J]. 地球物理学报, 50(4): 1216-1224. |
| [19] | 刘希强, 石玉燕, 曲均浩,等. 2009. 品质因子的尾波测定方法讨论[J]. 中国地震, 25(1): 11-23. |
| [20] | 牛滨华, 孙春岩. 2007. 半无限空间各向同性黏弹性介质与地震波传播[M]. 北京: 地质出版社. |
| [21] | 孙成禹. 2007. 地震波理论与方法[M]. 东营: 中国石油大学出版社. |
| [22] | 徐平, 王宝善. 张尉,等. 2006. 利用互相关函数求地震波衰减[J]. 地球物理学报, 49(6): 1738-1744. |
 2014, Vol. 29
2014, Vol. 29

