瞬变电磁应用采用电性源和回线源两种主要的装置类型(薛国强等, 2008,2011,2013,2014a,b;石显新等,2009;刘云鹤等,2012;吴小平等,2012;邱稚鹏等,2013;孙怀凤等,2013;李建慧等,2013),其中,回线源瞬变电磁垂直磁场分量得到最为广泛的研究和应用.
Poddar(1983)借助互易原理,对磁偶极子产生的频域电场切向分量沿边框进行线积分,推导出矩形发射回线在任一点激发的频率域垂直磁场表达式;Nabighian(1988)利用磁偶极源的响应对回线进行面积分,得到矩形回线和圆回线内外场的表达式;李建平等(2007)指出使用圆回线内接多边形进行电偶极源分解可以近似计算回线内场点的响应,在内接多边形的边数较少时符合实际应用;Xue等(2012)利用叠加原理,对电偶极子产生的场沿发射回线边框进行线积分,得到回线内外任一点的垂直磁场的计算公式.
近年来,矩形回线源磁场水平分量引起学者极大的关注.Chen等(2008)分析了常见异常体的瞬变电磁多分量的响应特征;席振铢等(2010)以磁偶极源叠加方式计算了回线源瞬变电磁多分量对板状体的分辨能力;武军杰等(2012)采用最小二乘方式计算回线源水平磁场分量的视电阻率;戚志鹏等(2011)以圆回线中心点和非中心点之间的相似性为依据,对回线非中心点水平磁场响应进行多项式拟合,给出视电阻率的多项式定义.
薄层地质结构体的有效探测问题一直是地球物理勘探理论及各种地球物理方法应用研究中面临的重要问题.回线源磁场垂直分量对薄层研究较多,唐新功等(1999)计算了距离发送源不同位置的2个三维导电薄板的电磁场响应,但是没有分析目标体厚度变化时瞬变场的响应规律; Li等(2005)结合自适应收缩性遗传算法与视纵向电导微分成像法,反演瞬变电磁测深中的导电薄层,该算法可以提高瞬变电磁法识别地下薄层的能力.但没有进一步讨论当装置及地下薄层结构分别发生变化时,瞬变电磁法识别目标体的能力; 薛国强和邓湘(2007)对比薄层存在与不存在时的视电阻率曲线,给出分辨极限的定量的判定依据,分析了不同地电模型下的垂直磁场分量对薄层的分辨能力,并进一步对瞬变电磁和可控源音频大地电磁对薄层的分辨能力进行了对比,但结论都是针对垂直磁场分量的单一分量得到的.
本文开展水平分量对薄层的分辨能力的比较研究.利用大定源回线瞬变电磁水平电场、水平磁场、垂直磁场分量的计算公式,在不同深度、不同厚度、不同电阻率情形下,计算了各响应分量与均匀半空间响应的相对误差并进行对比分析,给出各分量对薄层的厚度、埋深和电阻率的分辨极限,并给出各分量对薄层的分辨能力的对比结果,指出使用瞬变电磁多分量探测薄层的最优方案.
1 多分量计算对于大回线源装置,目前主要采用地表发射地表接收的观测方式.回线电磁场的计算是通过水平电偶极源沿各边进行线积分得到的.首先给出水平层状介质下,位于地表的x 方向水平电偶极源阶跃激发(不含接地项)在地表产生的各分量的表达式(Nabighian,1988):
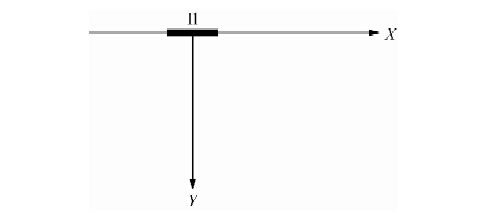 | 图 1 电偶极源示意图 Fig. 1 Sketch map of electric dipole |
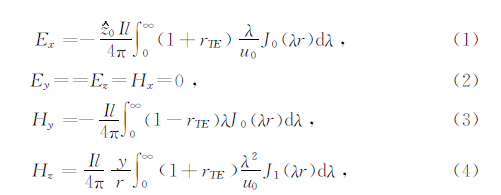
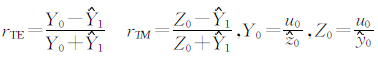
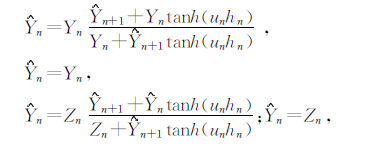
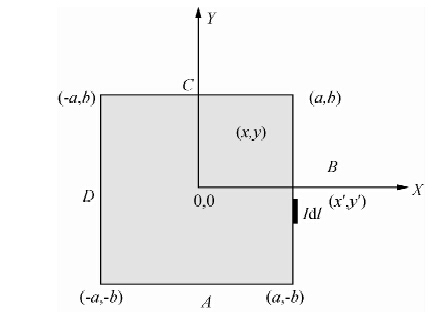 | 图 2 回线源偶极子叠加计算示意图 Fig. 2 Dipole superposition of loop source |
在给出水平电偶极源的瞬变电磁场表达式后,进一步给出回线源瞬变场计算的积分表达式,对于各边dl分别以dx′或dy′ 代替,垂直磁场分量的表达式为
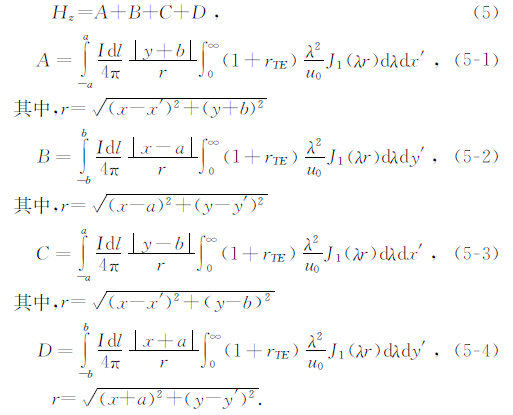
只有A和C边产生x方向的水平电场,B和D产生y方向的水平电场,因此,
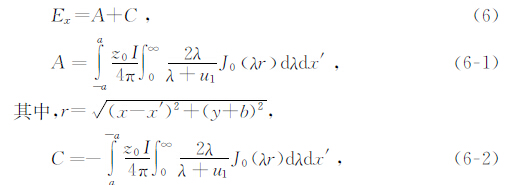
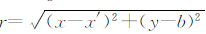
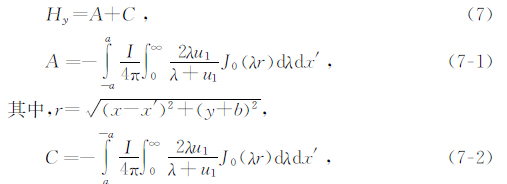
为了对各分量对薄层的分辨能力进行对比,选取如下的装置参数:发射回线200 m×200 m,发射电流10 A,选取(20,60)点作为观测位置.
薄层存在的地质模型:
低阻模型
ρ1=100 Ωm,ρ2=10 Ωm,ρ3=100 Ωm , H1=50 m,H2=2 m ;
高阻模型
ρ1=100 Ωm,ρ2=1000 Ωm,ρ3=100 Ωm , H1=50 m,H2=10 m .
与之对比的是不含薄层的均匀半空间的模型.
在其他参数完全相同的情况下,使用(5)式计算含薄层和均匀半空间的垂直磁场分量,使用(6)式计算含薄层和均匀半空间的水平电场Ex分量,使用(7)式计算含薄层和均匀半空间的水平磁场Hy分量,分析了含薄层模型与均匀半空间两种情况下的相对误差.根据以往的相对误差的计算方式,以均匀半空间介质的响应为基准,给出薄层响应相对误差计算公式为
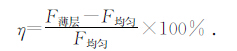
由图 3可见,低阻薄层的水平磁场分量(Hy)响应差别最大,达到32%,水平电场分量(Ex)的相对误差达到24%,相比于水平磁场的差别稍小,但大于垂直磁场分量的相对误差(21%),因此,我们认为水平磁场对低阻薄层的分辨能力最强,水平电场其次,垂直磁场分量最弱.
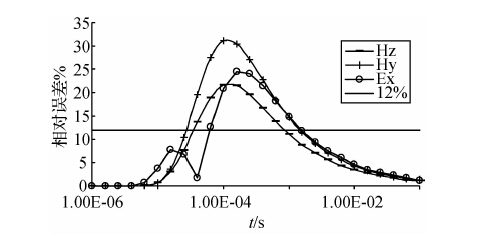 | 图 3 低阻模型情形的不同分量的相对误差的对比曲线 Fig. 3 Comparison curves of different components for low-resistivity models |
由图 4可见,高阻薄层的水平磁场响应差别最大,达到13%,大于薄层分辨的极限,而水平电场和垂直磁场分量均小于12%,不能达到分辨的下限,说明在该参数下的垂直磁场分量和水平电场对高阻薄层分辨能力较差.因此,我们认为水平磁场对高阻薄层的分辨能力最强,水平电场其次,垂直磁场分量最弱,但整体上说,电磁场各分量对高阻薄层的分辨能力相对低阻薄层的分辨能力要差很多.
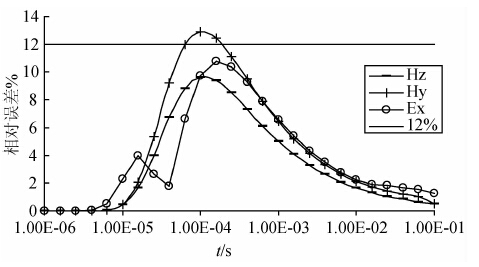 | 图 4 高阻模型情形的不同分量的相对误差的对比曲线 Fig. 4 Comparison curves of different components for high-resistivity models |
随着薄层的厚度的变化,响应的相对误差会产生变化,我们利用和上一节相同的装置参数,改变薄层的厚度,分析薄层厚度变化对响应相对误差的影响,给出各分量对薄层厚度的分辨极限.
3.1 低阻模型ρ1=100 Ωm,ρ2=10 Ωm,ρ3=100 Ωm , H1=50 m,H2=0.5,1,1.5 m .
在薄层与围岩电阻率差异为10倍关系时,当厚度为0.5 m时,各分量响应的相对误差均未达到12%;当厚度为1 m时,水平磁场分量的相对误差达到15%,超过分辨响应的下限,具有较好的分辨能力,水平电场的相对误差刚好达到12%,对低阻薄层可以分辨,垂直磁场分量响应的相对误差只有10%左右,并未达到分辨下限,认为不可分辨.因此,我们可以认为在电阻率差异为10倍的情形下,水平磁场对厚度的分辨极限在1%~2%之间,水平电场对厚度的分辨极限是2%,而垂直磁场分量的响应相对误差在厚度达到1.5 m时才可以分辨,即垂直磁场分量对厚度的分辨极限是在2%~3%之间.整体上说,水平分量对低阻薄层的分辨能力更强,水平磁场相比于水平电场分辨能力更强,垂直磁场分量对低阻的分辨能力稍弱.
3.2 高阻薄层
对于高阻薄层的情况,给出薄层厚度变化的模型:
ρ1=100 Ωm,ρ2=1000 Ωm,ρ3=100 Ωm , H1=50 m,H2=5,10,12,15 m.
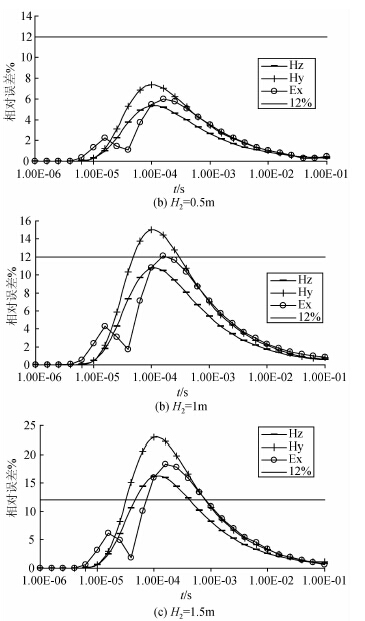 |
图 5 低阻薄层厚度变化对各分量响应相对误差影响的变化曲线 (a)H2=0.5 m;(b)H2=1 m;(c)H2=1.5 m. Fig. 5 Comparison curves of relative errors of different components with varying thickness for low-resistivity models |
在薄层与围岩电阻率差异为10倍关系时,当厚度为5 m时,各分量响应的相对误差均未达到12%;当厚度为10 m时,水平磁场分量的相对误差达到13%,超过分辨响应的下限,具有较好的分辨能力;水平电场和垂直磁场分量的相对误差未达到12%,并未达到分辨下限,水平电场直到薄层厚度达到12 m时,才可以分辨薄层,而垂直磁场分量直到薄层厚度接近15 m时才达到分辨的下限.因此,我们可以认为在电阻率差异为10倍的情形下,水平磁场对高阻薄层厚度的分辨极限在20%左右,水平电场对厚度的分辨极限是24%,而垂直磁场分量对厚度的分辨极限是在24%~30%之间.整体上说,鉴于各分量对低阻薄层的分辨能力相对较强,瞬变电磁各分量对高阻的分辨能力整体较差.相对而言,水平分量对高阻薄层的分辨能力稍强,垂直磁场分量对低阻的分辨能力稍强.
4 薄层的埋藏深度发生变化时的分辨能力对比
随着薄层的埋深的变化,响应的相对误差会产生变化,我们利用和上一节相同的装置参数,改变薄层的埋深,分析薄层埋深变化对响应相对误差的影响,给出各分量对薄层埋深的分辨极限.
4.1 低阻模型
ρ1=100 Ωm,ρ2=10 Ωm,ρ3=100 Ωm ,H1=0,10,20,50,120,150 m,H2=2 m.
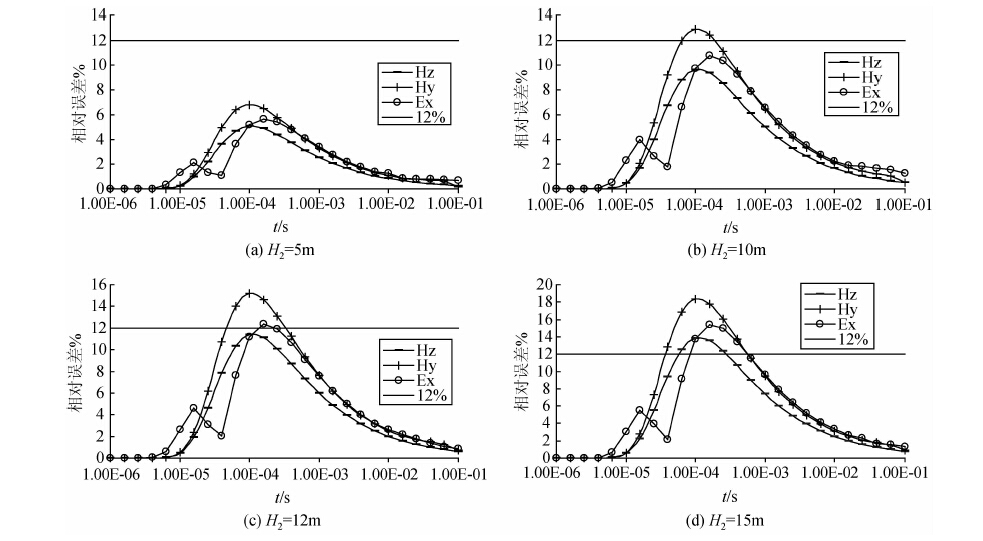 |
图 6 高阻薄层厚度变化对各分量响应相对误差影响的变化曲线 (a)H2=5 m;(b)H2=10 m;(c)H2=12 m;(d)H2=15 m. Fig. 6 Comparison curves of relative errors of different components with varying thickness for high-resistivity models |
由图 7可见,对于相同的薄层电阻率和厚度,随着埋藏深度的减小,各分量响应的相对误差逐渐增大,在埋深为0的极限情况下,地质结构变为两层模型,即我们经常提到的低阻屏蔽层.由图 7a可见,在小于1 ms的时间范围内,低阻薄层引起的响应差别都在可分辨的范围内,也就是说,我们在1 ms的时间范围内勘探的深度只有薄层的厚度,严重影响了瞬变电磁测深的深度要求.各分量之间对比来看,水平分量(水平磁场和电场)受表层低阻的影响的时间范围更大,即水平分量受到低阻屏蔽层的影响,有效探测深度更小.
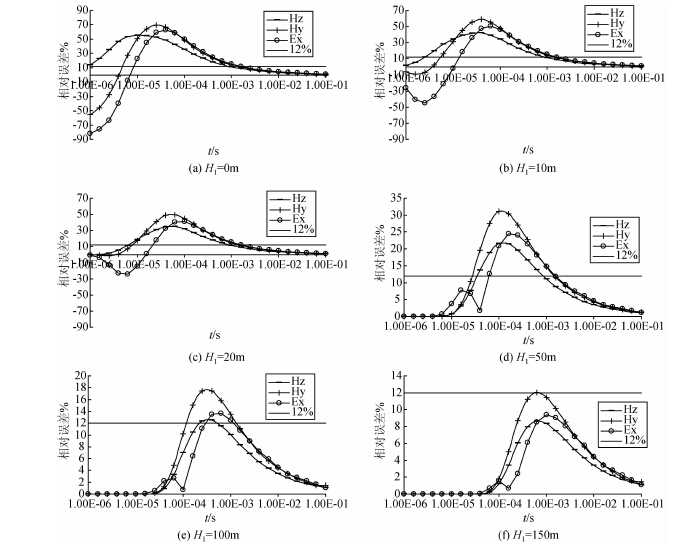 |
图 7 低阻薄层埋深变化对各分量响应相对误差影响的变化曲线 (a)H1=0 m;(b)H1=10 m;(c)H1=20 m;(d)H1=50 m;(e)H1=100 m;(f)H1=150 m. Fig. 7 Comparison curves of relative errors of different components with varying burial depth for low-resistivity models |
随着埋藏深度的增大,各分量对低阻薄层的分辨能力下降,在埋深达到120 m时,水平磁场的响应相对误差依然大于分辨的下限,对薄层可以分辨,直到埋深达到150 m时,相对误差达到分辨的下限,因此,水平磁场对低阻薄层埋深的分辨极限是75 m,即其对低阻薄层厚度的分辨极限是1.33%,与厚度变化时的结论一致,相应的其他分量对埋深的分辨极限也与厚度变化时结论一致.
另一方面,与前面的图对比,发现水平电场的极大值出现的时刻稍晚于磁场分量,通过多分量的瞬变场的观测有利于控制薄层的埋深和厚度.
4.2 高阻模型
ρ1=100 Ωm,ρ2=1000 Ωm,ρ3=100 Ωm,H1=0,10,20,30,40,50 m,H2=10 m.
随着埋藏深度的减小,各分量响应的相对误差逐渐增大,在埋深为0的极限情况下,地质结构变为两层模型,相比于低阻覆盖层的情况,高阻薄层影响的时间范围相差一个数量级,只有0.1 ms,而且响应的相对误差也远小于低阻薄层引起误差值.整体上说,瞬变场各分量对高阻的穿透能力较强,尤其是垂直磁场分量分量,受高阻薄层影响的时间范围最小,即穿透高阻的能力最强,对高阻的分辨能力稍弱于水平磁场和电场分量.
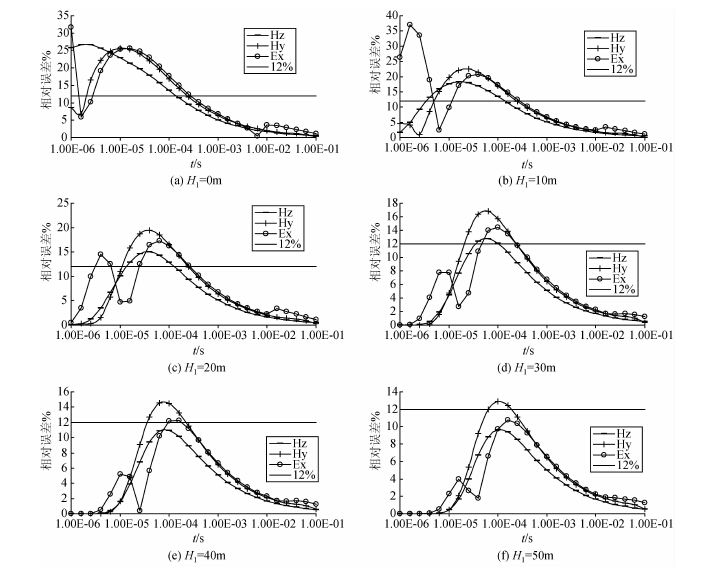 |
图 8 高阻薄层埋深变化对各分量响应相对误差影响的变化曲线 (a)H1=0 m;(b)H1=10 m;(c)H1=20 m;(d)H1=30 m;(e)H1=40 m;(f)H1=50 m. Fig. 8 Comparison curves of relative errors of different components with varying burial depth for high-resistivity models |
同时,随着埋深的增大,各分量响应的相对误差减小较快,埋深达到50 m时,只有水平磁场对薄层依然可以分辨,水平电场和垂直磁场分量已经不可分辨薄层的存在,各分量对薄层埋深的分辨能力与对厚度的分辨极限相互验证.
5 薄层电阻率发生变化时的分辨能力对比
薄层和围岩的电阻率的倍数关系发生变化时,响应的相对误差也会发生变化,给出薄层电阻率变化时的响应相对误差的对比图 9.
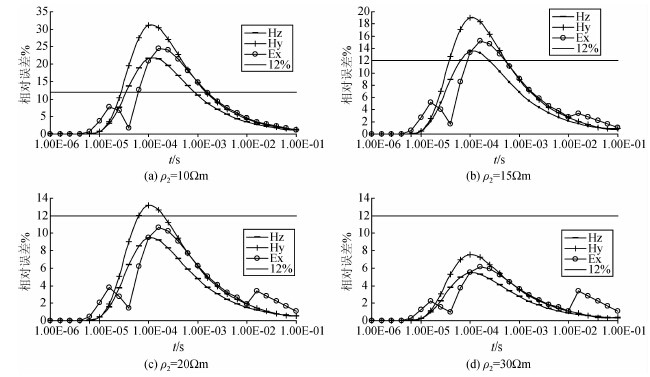 |
图 9 低阻薄层电阻率变化对各分量响应相对误差影响的变化曲线 (a)ρ2=10 Ωm;(b)ρ2=15 Ωm;(c)ρ2=20 Ωm;(d)ρ2=30 Ωm. Fig. 9 Comparison curves of relative errors of different components with varying resistivity for low-resistivity models |
ρ1=100 Ωm,ρ2=10,15,20,30 Ωm,ρ3=100Ωm , H1=50 m,H2=2 m.
在围岩电阻率设定的情况下,随着薄层电阻率由小变大,各分量对薄层的分辨力下降,当薄层的电阻率达到20 Ωm 时,垂直磁场分量和水平电场响应的相对误差小于分辨下限,已不可分辨,在埋深50 m,厚度2 m的情形下,各分量对低阻薄层的电阻率分辨极限可以用薄层与围岩电阻率比率表示,水平磁场为20%,水平电场和垂直磁场分量在15%~20%之间.
5.2 高阻薄层的电阻率的变化ρ1=100 Ωm,ρ2=600,800,900,1000,2000,5000 Ωm,ρ3=100 Ωm , H1=50 m,H2=10 m.
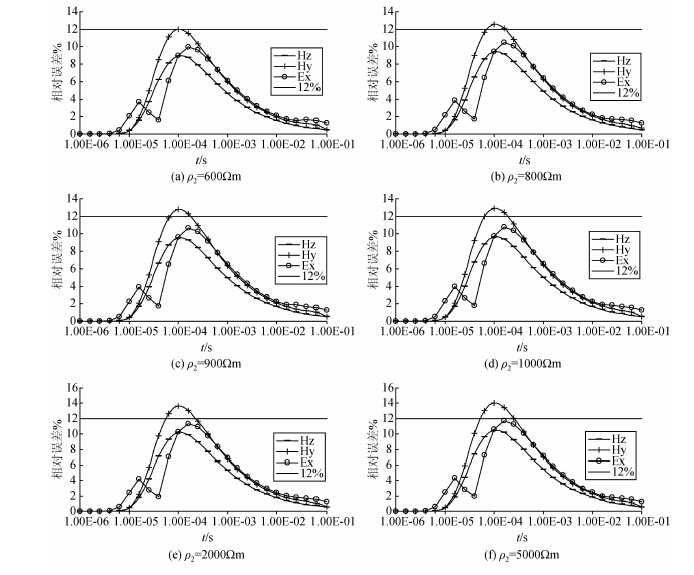 |
图 10 高阻薄层电阻率变化对各分量响应相对误差影响的变化曲线 (a)ρ2=600 Ωm;(b)ρ2=800 Ωm;(c)ρ2=900 Ωm;(d)ρ2=1000 Ωm;(e)ρ2=2000 Ωm;(f)ρ2=5000 Ωm. Fig. 10 Comparison curves of relative errors of different components with varying resistivity for high-resistivity models |
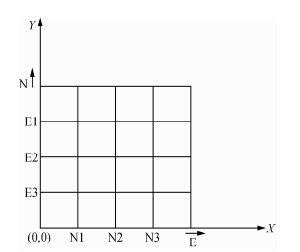 | 图 11 测线布置图 Fig. 11 Layout of survey lines |
在围岩电阻率设定的情况下,随着薄层电阻率由小变大,逐渐远离围岩电阻率,各分量对薄层的分辨力增加,但增加缓慢,当薄层的电阻率达到600 Ωm 时,水平磁场对薄层变得可以分辨,因此,在埋深50 m,厚度10 m的情形下,当薄层电阻率达到围岩的6倍时,水平磁场对薄层可以分辨,垂直磁场分量和水平电场分辨能力更差,水平电场响应的相对误差只有薄层电阻率达到围岩的50倍才可以分辨,垂直磁场分量需要更大的电阻率差别.
6 实例分析为了对理论计算结果进行验证,在河北某铁矿区进行回线源瞬变电磁勘查试验工作,该区域浅部为高阻覆盖层,中深部夹有低阻铁矿.瞬变电磁仪器选用加拿大生产的V8多功能电法仪.本次工作采用参数:发射线圈100 m×100 m,测线长度为100 m,选用8.3 Hz基频进行工作,观测时窗为:0.216 ms~25.92 ms.
图 12是对应测点的磁场垂直分量和水平分量的相应对比结果,虚线表示磁场垂直分量,实线表示磁场水平分量.
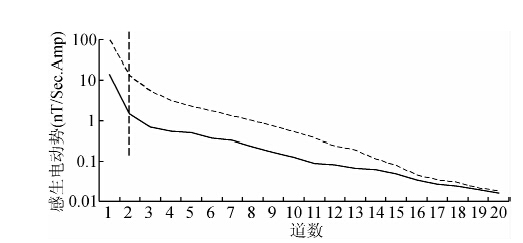 | 图 12 实测磁场水平分量与垂直分量对比 Fig. 12 Comparison curves of observed horizontal and vertical component |
由图 12可见,在早期道,磁场水平分量曲线斜率比垂直分量要大,表明磁场水平分量衰减更加迅速,根据高电阻率时响应曲线衰减较快的特征,可以推断磁场水平分量对高阻的反应更加敏感,很好了验证了前面理论模型得出的结论:水平磁场对薄层的分辨能力较强,垂直磁场分量相对最弱.
通过将每一道均匀半空间瞬变电磁响应正演计算结果与已知瞬变电磁响应数据进行拟合,得到满足已知瞬变电磁响应数据的均匀半空间正演模型参数,将其电阻率定义为视电阻率.这里,我们将利用二分法求全时域视电阻率.
图 13给出了E2线的视电阻率剖面.图 13a为水平磁场分量的视电阻率剖面,图 13b为垂直磁场分量的视电阻率剖面.
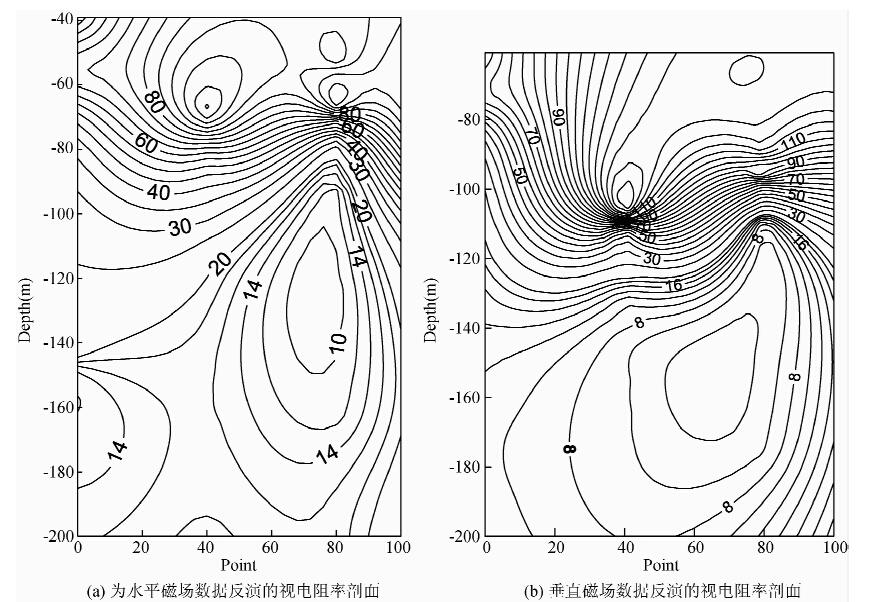 |
图 13 E2线的视电阻率剖面 (a)为水平磁场数据反演的视电阻率剖面;(b)垂直磁场数据反演的视电阻率剖面. Fig. 13 Apparent resistivity section of E2 line |
由图 13可见,水平磁场分量反演的视电阻率剖面与垂直磁场分量反演的视电阻率剖面整体形态相似,异常体的位置大致相当.但水平磁场反演的视电阻率剖面可以清晰的判断异常体的位置,集中于40-90号测点的范围内,符合已知 矿区的实际情况;而垂直磁场分量反演的视电阻率剖面低阻异常贯穿整条测线,异常体的边界不明确.因此,磁场水平分量的观测有利于进一步提升瞬变电磁法对地质体的分辨能力.
7 结 论
7.1 在含薄层的不同模型下,通过对大定源回线各分量的正演计算与不含薄层的均匀半空间的响应的相对误差的对比,我们发现水平磁场对薄层的分辨能力最强,水平电场次之,垂直磁场分量相对最弱.因此,对于夹低阻薄层的情况,可以使用水平分量进行观测,进一步提升瞬变电磁法对薄层的分辨能力.但对于薄层位于地表的低阻覆盖层问题,垂直磁场分量受低阻覆盖层的影响时间要小于水平磁场和电场,更利于在低阻覆盖区进行瞬变场的探测工作.
7.2 相对于各分量对低阻薄层的高分辨能力,各分量对高阻薄层分辨能力很差,但各分量对高阻薄层有很好的穿透能力,受高阻薄层的影响的时间很短,可以实现高阻区的大深度探测.同时,各分量对薄层分辨最佳时刻的不同,有利于使用多分量观测对薄层埋深及厚度的控制,为多分量TEM全域探测提供了依据.
7.3 通过实例分析验证了上述结论,因此,我们建议使用多分量的观测方式,进一步提高瞬变电磁法对薄层的分辨能力和解释精度.
致 谢 感谢本文匿名审稿人和编辑给予文章内容和格式上的帮助!
| [1] | Chen C S, Chiu W H, Lin C R. 2008. Three component time-domain electromagnetic surveying: modeling and data analysis[J]. Piers Online, 4(4): 475- 480. |
| [2] | Kaufman A A, Keller G V. 1983. Frequency and Transient Soundings[M]. New York: Elsevier. |
| [3] | Li J H, Zhu Z Q, Zeng S H, et al. 2012. Progress of forward computation in transient electromagnetic method [J]. Progress in Geophysics (in Chinese), 27(4): 1393-1400. |
| [4] | Li J H, Hu X Y, Zeng S H, et al. Three dimensional forward calculation for loop source transient electromagnetic method based on electromagnetic Helmholtz equation[J]. Chinese J. Geophys. (in Chinese), 56(12):4256-4267. |
| [5] | Li J P, Li T L, Zhao X F, et al. 2007. Study on the TEM all-time apparent resistivity of arbitrary shape loop source one the layered medium[J]. Progress in Geophysics (in Chinese), 22(6): 1777-1780. |
| [6] | Li X, Xue G Q, Song J P, et al. 2005. Application of the adaptive shrinkage genetic algorithm in the feasible region to TEM conductive thin layer inversion [J]. Applied Geophysics, 12(4): 204-211. |
| [7] | Liu Y H, Yin C C, Weng A H, et al.. 2012. Attitude effect for marine CSEM system [J]. Chinese J. Geophys. (in Chinese) ,55(8):2757-2768. doi:10.6038/j.issn.0001-5733.2012.08.027. |
| [8] | Nabighian M N. 1988. Electromagnetic Methods in Applied Geophysics, Volume 1: Society of Exploration Geophysicists[M]. Tusla: Society of Exploration Geophysicists, 203-252. |
| [9] | Poddar M. 1983. A rectangular loop source of current on multilayered earth [J]. Geophysics, 48(1): 107-109. |
| [10] | Qi Z P, Li X, Zhu H W, et al. 2011. Definition of apparent resistivity for non-center vertical component of large-loop TEM configuration [J]. Progress in Geophysics (in Chinese), 26(4): 1350-1358. |
| [11] | Qi Z P, Li X, Guo W B, et al. 2011. Definition of apparent resistivity for horizontal-component of transient electromagnetic method[J]. Journal of China Coal Society (in Chinese), 236(Suppl): 88-93. |
| [12] | Qiu Z P, Li Z H, Li D Z, et al.2013. Non-orthogonal-Grid-based three dimensional modeling of transient electromagnetic field with topography [J]. Chinese J. Geophys. (in Chinese), 56(12):4245-4255. |
| [13] | Shi X X, Yan S, Fu J M, et al. 2009. Improvement for interpretation of central loop transient electromagnetic method [J]. Chinese J. Geophys. (in Chinese), 52(7): 1931-1936. |
| [14] | Sun H F, Li X, Li S C, et al. Three dimensional FDTD Sun H F, Li X, Li S C, et al. Three dimensional FDTD modeling of TEM excited by a loop source considering ramp time[J]. Chinese J. Geophys. (in Chinese),56(3):1049-1064. |
| [15] | Tang X G, Hu W B, Yan L J. 1999. Comparing transient electromagnetic response of multiple 3D conductive sheets [J]. Jianghan Petroleum Institute (in Chinese), 21(4): 57-60. |
| [16] | Wu J J, Wang X C, Deng X H, et al. 2012. The method for calculation x-component apparent resisitivity of TEM fixed-loop[J]. Geophysical and Geo-exploration (in Chinese), 36(4): 684-687. |
| [17] | Xi Z Z, Liu J, Long X, et al. 2010. Three-component measurement in transient electromagnetic method[J]. Journal of Central South University (Natural Science) (in Chinese), 41(1): 272-276. |
| [18] | Xue G Q, Deng X. 2007. Capacity of transient electromagnetic method for detecting thin layer [J]. OGP (in Chinese), 42(6): 709-713. |
| [19] | Xue G Q, Li X, Di Q Y. 2008. Research progress in TEM forward modeling and investigation and inversion calculation [J]. Progress in Geophysics (in Chinese), 23(4): 1165-1172. |
| [20] | Xue G Q, Yan S, Zhou N N. 2011. Theoretical study on the errors caused by dipole hypothesis of large loop TEM response[J]. Chinese J. Geophys. (in Chinese),54(9):2389-2396. |
| [21] | Xue G Q, Bai C Y, Yan S, et al. 2012. Deep sounding TEM investigation method based on a modified fixed central-loop system[J]. Journal of Applied Geophysics, 76: 23-32. |
| [22] | Xue G Q,Chen W Y,Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding [J].Chinese Journal of Geophysics, 56(1):255-261. |
| [23] | Xue G Q, Yan S, Chen W Y. 2014a. Research prospect to grounded-wire TEM with short-offset [J]. Progress in geophys. (in Chinese), 29(1):177-181. |
| [24] | Xue G Q, Wang H Y, Yan S, et al.. 2014b. Time-domain Green function solution for transient electromagnetic field [J]. Chinese Journal of Geophysics,57(2):671-678. |
| [25] | Zhou N N, Xue G Q, Li M F, et al. 2011. Response of polygonal loop based on dipole approximation [J]. Coal Geology and Exploration (in Chinese), 39(4): 49-54. |
| [26] | 李建慧, 朱自强, 曾思红,等. 2012. 瞬变电磁法正演计算进展[J]. 地球物理学进展, 27(4): 1393-1400. |
| [27] | 李建慧,胡祥云,曾思红,等.2013.基于电场Helmholtz方程的回线源瞬变电磁法三维正演[J].地球物理学报,56(12):4256-4267. |
| [28] | 李建平, 李桐林, 赵雪峰,等. 2007. 层状介质任意形状回线源瞬变电磁全区视电阻率的研究[J]. 地球物理学进展, 22(6): 1777-1780. |
| [29] | 刘云鹤,殷长春,翁爱华,等. 2012. 海洋可控源电磁法发射源姿态影响研究. 地球物理学报,55(8):2757-2768. doi:10.6038/j.issn.0001-5733.2012.08.027. |
| [30] | 戚志鹏, 李貅, 朱宏伟,等. 2011. 大定源装置下瞬变电磁法视电阻率定义[J]. 地球物理学进展, 26(4): 1350-1358. |
| [31] | 戚志鹏, 李貅, 郭文波,等. 2011. 瞬变电磁水平分量视电阻率定义[J]. 煤炭学报, 36(增): 88-93. |
| [32] | 邱稚鹏,李展辉,李墩柱,等.2013.基于非正交网格的带地形三维瞬变电磁场模拟[J].地球物理学报,56(12):4245-4255. |
| [33] | 石显新, 闫述, 傅君眉,等. 2009. 瞬变电磁法中心回线装置资料解释方法的改进[J]. 地球物理学报, 52(7): 1931-1936. |
| [34] | 孙怀凤,李貅,李术才,等.2013.考虑关断时间的回线源激发TEM 三维时域有限差分正演[J].地球物理学报,56(3):1049-1064. |
| [35] | 唐新功, 胡文宝, 严良俊. 1999. 多个三维薄板瞬变电磁响应的比较[J]. 江汉石油学院学报, 21(4): 57-60. |
| [36] | 武军杰, 王兴春, 邓晓红,等. 2012. 定源回线瞬变电磁 x 分量视电阻率计算方法[J]. 物探与化探, 36(4): 684-687. |
| [37] | 席振铢, 刘剑, 龙霞等. 2010. 瞬变电磁三分量测量方法研究[J]. 中南大学学报(自然科学版), 2010, 41(1): 272-276. |
| [38] | 薛国强, 邓湘. 2007. 瞬变电磁法对薄层的探测能力[J]. 石油地球物理勘探, 42(6): 709-713. |
| [39] | 薛国强, 李貅, 底青云2008. 瞬变电磁正反演问题研究进展[J]. 地球物理学进展, 23(4): 1165-1172. |
| [40] | 薛国强,闫述,周楠楠. 2011. 偶极子假设引起的大回线源瞬变电磁响应偏差分析[J]. 地球物理学报,54(9):2389-2396. doi:10.3969/j.issn.0001-5733.2011.09.022. |
| [41] | 薛国强,陈卫营,周楠楠,等. 2013. 接地源瞬变电磁短偏移深部探测技术[J]..地球物理学报, 56(1):255-261. doi:106038/cjg20130126. |
| [42] | 薛国强,闫述,陈卫营. 2014a. 接地源短偏移瞬变电磁法研究展望[J]. 地球物理学进展,29(1):177-181. doi:10.6308/pg10140124. |
| [43] | 薛国强,王贺元,闫述,等.2014b.瞬变电磁场时域格林函数解[J].地球物理学报,57(2):671-678. |
| [44] | 周楠楠, 薛国强, 李梅芳,等. 2011. 基于电偶极子近似的多边形回线源瞬变电磁响应[J]. 煤田地质与勘探, 39(4): 49-54. |
 2014, Vol. 29
2014, Vol. 29

