2. 中国石油大学(华东) 地球科学与技术学院, 青岛 266580;
3. 中国地质大学(北京) 海洋学院, 北京 100083
2. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China;
3. School of Marine Science, China University of Geoscience (Beijing), Beijing 100083, China
随着计算机模拟技术的发展,蒙特卡罗模拟方法在物理学(Ye et al., 2011;徐英和洪治,2012)、化学(Dai et al., 2012)、热力学(王文和史琳,2002;赵胜喜等,2012)、医学(王屏等,2012;Ding et al., 2012)、经济学(柴洪和马竹书,2012;陈国栋,2012)及建筑学(Tan,2012)等都有广泛的应用.实际科学计算中问题往往是多维的,而问题难度随维数呈指数上升,传统数值方法难以解决这种问题;而蒙特卡罗方法研究问题的复杂性不依赖于问题的维数,所以能很好的处理多维问题(方再根,1988).
目前研究放射性测井问题的计算机模拟方法主要有两种:一是利用扩散理论建立波尔兹曼方程并求解(黄隆基,1985),但建立的方程多为多变量微分方程,不能得到解析解,且数值解求解复杂;二是利用蒙特卡罗方法对给定的问题建立随机抽样模型,并用一系列随机数跟踪大量粒子历程的方法完成对粒子输运的模拟(Gardner et al., 2007).利用蒙特卡罗模拟方法可方便的改变各种实验条件,并且可实现实体物理实验很难实现或实现不了的实验条件,解决问题具有低成本、周期短的特点.所以,蒙特卡罗数值模拟方法为研究放射性问题提供了一种简便有效的方法,在放射性测井技术基础方法研究及仪器研发中具有重大的意义.
本文从方法原理上介绍蒙特卡罗模拟方法,并建立不同的数值计算模型,利用具体的模拟实例说明蒙特卡罗方法在放射性测井中的应用,主要表现在核物理场分布、放射性测井新方法研究、测井仪器参数优化设计和测井响应及数据处理方法等四个方面.
1 蒙特卡罗数值计算方法蒙特卡罗方法解决的基本问题是数值求积,下面利用简单问题说明蒙特卡罗数值求积方法(周铁等,2006).
设有一个数值求积问题为


由弱大数定理,IN(f)将依概率收敛到I(f).IN(f)作为一个随机变量有
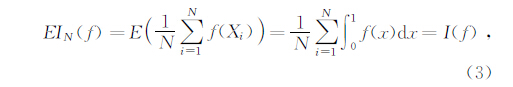
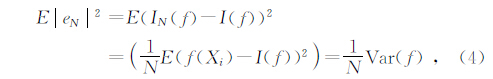
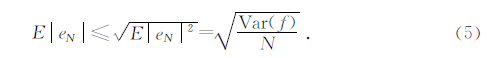
蒙特卡罗方法模拟辐射输运的思想在19世纪40年代由美国实验室的科学家提出Los Alamos,1976年开发出了通用程序MCNP(a general Monte Carlo code for Neutron and Particle transport).MCNP是一套通用的、模拟三维空间中连续能量的中子、光子和电子联合输运的程序,中子和光子在物质中输运的宏观表现是大量粒子与原子核微观作用的平均结果.该方法建立一个概率模型或随机过程,通过逐一模拟和记录单个粒子的历程,根据中子及光子已知的分布函数,对中子或光子与原子核发生碰撞时的位置、能量、运动方向、反应类型、源分布等方面进行抽样,其平均结果反映中子和光子在物质中的输运(Briesmeister,2000).
图 1为模拟中一个中子射入物质后的随机历程,如图所示,中子在1点发生碰撞,根据中子与物质的作用分布函数,抽取随机数确定反应类型,在此处抽取非弹性散射反应,放出非弹性散射伽马及中子;在2点与原子核发生(n,2n)反应,其中一个出射中子射出物质,另一个中子在3点被吸收.并产生一个光子在5点与物质发生散射作用离开物质,单粒子作用历史结束.MCNP通过跟踪大量粒子的作用历程,最终确定测井过程中发射中子与仪器、井眼、地层等物质元素原子核发生作用的宏观效果.
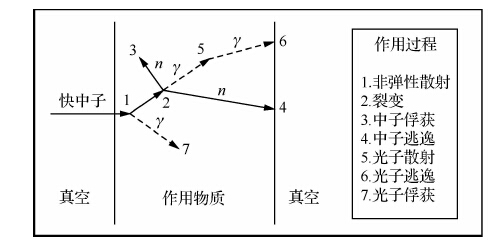 | 图 1 单个中子随机历史 Fig. 1 The r and om history of a neutron |
用蒙特卡罗程序(MCNP)建立地层模型模拟计算中子、光子在地层中的输运时,用到的命令卡包括标题卡、栅元卡、曲面卡、数据卡,其中数据卡包括类型卡、栅元参数卡、曲面参数卡、源卡、计数卡,图 2为利用蒙特卡罗方法建立的套管井条件下的地层模型示意图.
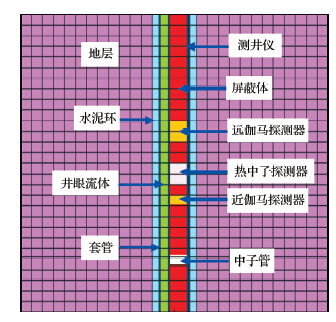 | 图 2 蒙特卡罗计算模型纵截面示意图 Fig. 2 Vertical cross-section of Monte Carlo simulation model example |
利用蒙特卡罗方法可方便的建立各种地层模型,针对放射性测井中的问题可开展核物理场分布、放射性测井新方法、测井仪器参数优化设计和测井响应及数据处理方法等方面的研究.
3.1 核物理场分布模拟利用蒙特卡罗方法建立地层模型,记录地层中不同位置处粒子的计数,可以模拟地层自然伽马场、中子场、次生伽马场空间分布.对核物理场的分布研究,可以直观显示粒子与地层元素原子核的相互作用结果,得到粒子与物质作用的时间特性和空间特性,为研究不同测井方法提供理论依据.
图 3为利用Am-Be中子源时在不同孔隙度饱含水砂岩地层中热中子场的分布,通过对热中子场的分布研究得到热中子的分布范围在40 cm左右,孔隙度越低热中子的分布范围越广,孔隙度对热中子分布范围影响很大,这正是中子孔隙度测井的理论依据.通过研究中子场的分布规律,得出径向探测深度等特性,并根据场分布特点形成不同的测量方法.
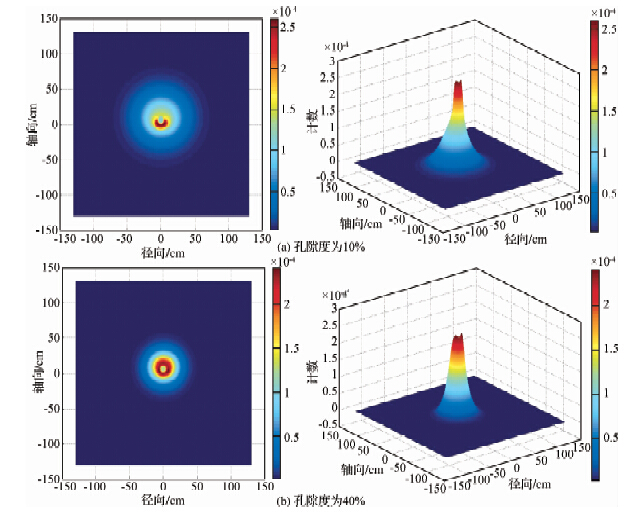 | 图 3 不同孔隙度砂岩地层中热中子场分布 Fig. 3 Distribution of thermal neutron field in s and stone formation with different porosity |
由于放射源会对人体和环境造成潜在的危害 (Committee on Radiation Source and Replacement, 2008),开展放射性实体物理实验存在很大困难,所以可以借助于数值模拟开展对放射性测井新方法的研究.本文中以对脉冲双伽马谱饱和度测井(张锋等,2010b;Zhang et al., 2011a; Zhang et al., 2011b)为例,说明蒙特卡罗模拟方法在放射性测井新方法研究中的应用.
图 4为脉冲中子双伽马谱饱和度测井采用的脉冲和时序设计,一个完整的测量时序分为3个时间段,在第一个时间段内中子源发射 中子并采集伽马时间谱和非弹性散射伽马能谱,第二个时间段内采集俘获伽马能谱,第三个时间段内记录本底能谱.
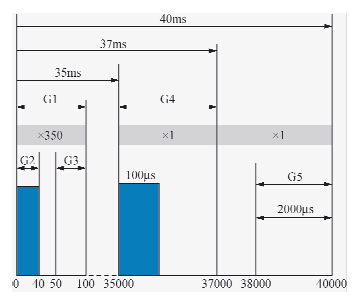 | 图 4 脉冲与测量时序设计 Fig. 4 Time sequence design of pulse emission and measurement |
利用蒙特卡罗方法建立地层模型,采用图 4所示的脉冲和测量时序,模拟计算同时记录伽马能谱和伽马时间谱,通过数据处理得出不同含油饱和度条件下C/O与宏观俘获截面交会图,如图 5所示.
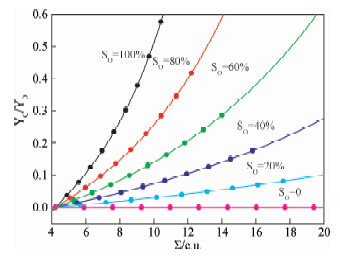 | 图 5 脉冲中子双伽马谱饱和度测井响应 Fig. 5 Logging response of pulsed-neutron dual gamma spectrum saturation logging |
从图 5可以看出,C/O与宏观俘获截面交会图上每一点表示在一定含油饱和度条件下C/O与宏观俘获截面值,地层孔隙度发生变化,其位置也随之改变,利用C/O与宏观俘获截面值的交会技术可以在孔隙度未知的情况下确定含油饱和度.
3.3 测井仪器参数优化设计粒子探测器类型、尺寸、屏蔽体、源距等是研制放射性测井仪器重要参数,利用蒙特卡罗数值模拟方法可开展测井仪器参数优化设计研究,为放射性测井仪器研制提供理论依据.
图 6为是在不同孔隙度地层中利用不同中子源时模拟的热中子随源距的变化关系(张锋等,2010a;张锋等,2010b),从图上可以看出利用D-D、Am-Be和D-T中子源时零源距分别大约为10 cm、12 cm和12 cm;获取零源距后,再根据探测器计数统计性及测井响应特征可以确定出最佳源距.图 7为不同粒子探测器能谱响应特性,从图中可以看出LaBr3探测器的能量分辨率最好,NaI探测器的次之,BGO探测器的最差.
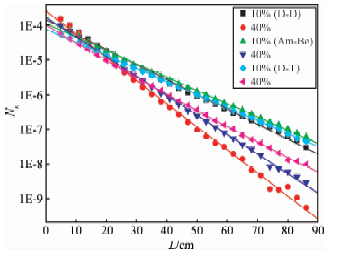 | 图 6 不同中子源时热中子计数与源距关系 Fig. 6 The relationship of thermal neutron counting and spacing with different neutron sources |
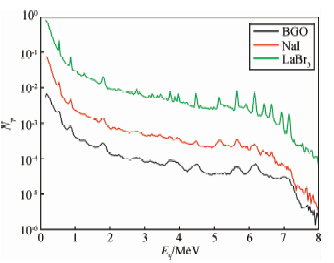 | 图 7 不同探测器响应特性 Fig. 7 Response feature of different detectors |
通过蒙特卡罗方法建立不同地层模型,可方便设定和改变各种地层条件,模拟记录粒子与元素原子核相互作用产生的时间谱或能谱,通过谱数据处理得到相应测井参数,建立和地质参数之间的测井响应关系,并研究各种因素对测井响应的影响,形成数据处理方法.
图 8为不同孔隙度条件下地层宏观俘获截面与含水饱和度的三维关系图,从图上可以看出孔隙度一定时地层宏观俘获截面与含水饱和度呈现良好的相关性,且随着孔隙度的增大,利用地层宏观俘获截面确定含水饱和度的灵敏度增大.图 9为模拟利用四个伽马探测器的随钻方位伽马测井仪器穿过不同厚度放射性地层的方位伽马成像图(袁超,2012),放射性地层的相对倾斜角度都为70°,图中从左向右模拟地层的厚度为40 cm、80 cm和100 cm,从图上可以看出放射性地层的厚度对方位伽马成像图的影响很大,厚度越大成像图在井轴方向的展布越大,利用方位伽马成像图可以确定出放射性地层的相对倾斜角度及地层厚度.
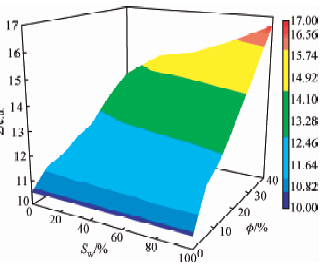 | 图 8 宏观俘获截面与含水饱和度和孔隙度的关系 Fig. 8 The relationship of macro capture cross section and water saturation under different porosity |
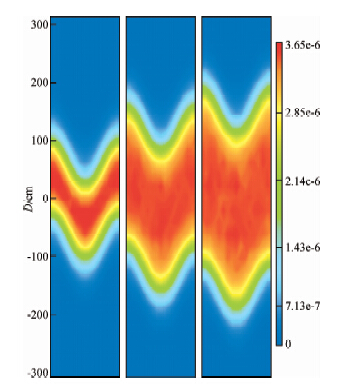 | 图 9 不同放射性地层厚度条件下方位自然伽马成像图 Fig. 9 Azimuthal gamma imaging in radioactive formations with different thickness |
4.1蒙特卡罗数值模拟是一种放射性测井中重要的数值模拟方法,可以方便的改变各种实验条件,且可实现实体物理实验很难实现或实现不了的实验条件,为放射性测井基础研究提供了简便有效的方法.
4.2 蒙特卡罗数值模拟方法在放射性测井中有四大方面应用:
1)核物理场分布模拟:通过模拟不同条件下中子场及伽马场分布,可给出径向探测深度等特性,并根据场分布特点形成不同的测量方法;
2)放射性测井新方法研究:避免实体物理实验存在的困难,通过数值模拟方法开展对放射性测井新方法的研究;
3)测井仪器参数优化设计:可实现探测器类型和尺寸、源距及屏蔽体等测井仪器关键参数的优化设计;
4)测井响应及数据处理方法研究:通过模拟计算得到的谱数据处理获得相应的测井参数,建立和地质参数之间的测井响应关系,并研究各种因素对测井响应的影响,形成数据处理及影响因素校正方法.
致 谢 感谢审稿专家和编辑部老师的热情帮助.| [1] | Briesmeister J F. 2000. MCNP-A General Monte Carlo N-Particle Transport Code[M]. Los Alamos: Los Alamos National Laboratory. |
| [2] | Chai H, Ma Z S. 2012. Risk assessment of financial affairs in projects based on Monte Carlo simulation[J]. Project Management Technology (in Chinese), 10(11): 79-82 |
| [3] | Chen G D. 2012. Sensitivity analysis of investment risk based on Monte Carlo simulation[J]. Finance and Accounting Monthly (in Chinese), (18) 59-61. |
| [4] | Committee on Radiation Source and Replacement. 2008. Radiation Source Use and Replacement: Abbreviated version[M]. Washington: The National Academies Press. |
| [5] | Dai W, Shui Z H, Shen C H, et al. 2012. Monte Carlo simulation on adsorption characteristics of water in kaolin [J]. Journal of the Chinese Ceramic Society, 40(1): 149-153. |
| [6] | Ding J J, Zhang Y J, Jiao Z, et al. 2012. The effect of poor compliance on the pharmacokinetics of carbamazepine and its epoxide metabolite using Monte Carlo simulation[J]. Acta Pharmacologica Sinica, 33(11): 1431-1440. |
| [7] | Fang Z G. 1988. Computer simulation and Monte Carlo method (in Chinese) [M]. Beijing: Beijing Industry Institute Press. |
| [8] | Gardner R P, Xu L B, Wang J X, et al. 2007. Some Lessons Learned From MCNP Usage[C]. Proceedings of the SPWLA 48th Annual Logging. Symposium, Paper K. |
| [9] | Huang L J. 1985. Theory of nuclear well logging (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [10] | Tan G. 2012. Natural ventilation performance of single room building with fluctuating wind speed and thermal mass[J]. Journal of Central South University, 19(3): 733-739. |
| [11] | Wang P, Gao X G, Zhang J L, et al. 2012. Use of Monte Carlo simulation to optimize vancomycin dosing regimens in MRSA-infected patients with renal dysfunction [J]. Chinese Journal of New Drugs (in Chinese), 21(3): 335-338. |
| [12] | Wang W, Shi L. 2002. Molecular dynamic simulation on the phase equilibria properties of alternative refrigerant[J]. Journal of Engineering Thermophysics (in Chinese), 23(4): 401-404. |
| [13] | Xu Y, Hong Z. 2012. Monte Carlo simulation of the effect of bias electric field on intensity of THz radiation[J]. Journal of Zhejiang University (Engineering Science) (in Chinese), 46(5): 899-904. |
| [14] | Ye T, Chai P, Gao J, et al. 2011. Investigation of scatter from out of the field of view and multiple scatter in PET using Monte Carlo simulations[J]. Chinese Physics C, 35(12): 1166-1171. |
| [15] | Yuan C. 2012. Fundamental study on LWD azimuthal Gamma Ray well logging (in Chinese) [Master thesis]. Shandong Qingdao: China University of Petroleum (East China). |
| [16] | Zhang F. 2008. A fundamental study on the new method for remaining oil saturation using pulsed neutron logging (in Chinese) [Doctoral thesis]. Shandong Qingdao: China University of Petroleum (East China). |
| [17] | Zhang F, Jin X Y, Hou S. 2010a. Monte Carlo simulation on compensated neutron porosity logging in LWD with D-T pulsed neutron generator [J]. Journal of Isotopes (in Chinese), 23(1): 15-21. |
| [18] | Zhang F, Yuan C. 2010. Monte Carlo simulation on compensated neutron porosity logging with D-D neutron generator [J]. Well Logging Technology (in Chinese), 34(3): 227-232. |
| [19] | Zhang F, Yuan C, Wang X G. 2010b. Study on the dual gamma spectrum saturation logging method based on pulsed neutron source and numerical simulation [J]. Chinese Journal of Geophysics (in Chinese), 53(10): 2527-2533, doi:10.3969/j.issn.0001-5733.2010.10.026. |
| [20] | Zhang F, Yuan C, Liu J T, et al. 2011a. Monitoring remaining oil by using pulsed neutron dual spectrum logging technology and its application[C]// SEG International Exhibition and 81st Annual Meeting. |
| [21] | Zhang F, Yuan C, Liu J T, et al. 2011b. Simulation on the method of determining remaining oil saturation by measuring dual pulsed neutron parameters[C]// SPE Reservoir Characterisation and Simulation Conference and Exhibition. |
| [22] | Zhao X S, Qi Y X, Yu Z G, et al. 2012. Monte Carlo simulation of thermodynamic properties of R32 [J]. Refrigeration (in Chinese), 40(11): 37-40. |
| [23] | Zhou T, Xu S F, Zhang P W, et al. 2006. Calculation Method (in Chinese) [M]. Beijing: Tsinghua University Press. |
| [24] | 柴洪, 马竹书. 2012. 基于蒙特卡罗模拟法的工程项目财务风险评估[J]. 项目管理技术, 10(11): 79-82. |
| [25] | 陈国栋. 2012. 基于蒙特卡罗模拟的投资项目风险敏感性分析[J]. 财会月刊, (18): 59-61. |
| [26] | 方再根. 1988. 计算机模拟和蒙特卡洛方法[M]. 北京: 北京工业学院出版社. |
| [27] | 黄隆基. 1985. 放射性测井原理[M]. 北京: 石油工业出版社. |
| [28] | 王屏, 高笑舸, 张坚磊,等. 2012. 应用蒙特卡罗模拟优化肾功能不全患者MRSA感染时万古霉素的给药方案[J]. 中国新药杂志, 21(3): 335-338. |
| [29] | 王文, 史琳. 2002. 制冷剂替代物相平衡性质的分子动力学模拟[J]. 工程热物理学报, 23(4): 401-404. |
| [30] | 徐英, 洪治. 2012. 偏置电场对THz辐射强度影响的蒙特卡罗模拟[J]. 浙江大学学报(工学版), 46(5): 899-904. |
| [31] | 袁超. 2012. 随钻方位伽马测井方法基础研究[硕士论文]. 青岛: 中国石油大学(华东). |
| [32] | 张锋. 2008. 脉冲中子剩余油饱和度测井新方法基础研究[博士论文]. 青岛: 中国石油大学(华东). |
| [33] | 张锋, 靳秀云, 侯爽. 2010a. D-T脉冲中子发生器随钻中子孔隙度测井的蒙特卡罗模拟[J]. 同位素, 23(1): 15-21. |
| [34] | 张锋, 袁超. 2010. 利用D-D中子发生器进行补偿中子孔隙度测井的模拟研究[J]. 测井技术, 34(3): 227-232. |
| [35] | 张锋, 袁超, 王新光. 2010b. 脉冲中子双伽马谱饱和度测井方法及数值模拟研究[J]. 地球物理学报, 53(10): 2527-2533, doi:10.3969/j.issn.0001-5733.2010.10.026. |
| [36] | 赵胜喜, 祁影霞, 喻志广,等. 2012. R32热力学性质的蒙特卡罗模拟[J]. 制冷技术, 40(11): 37-40. |
| [37] | 周铁, 徐树方, 张平文,等. 2006. 计算方法[M]. 北京: 清华大学出版社. |
 2014, Vol. 29
2014, Vol. 29

