2. 中南大学 地球科学与信息物理学院, 长沙 410083;
3. 西北综合勘察设计研究院, 西安 710003
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Northwest research Institute of Engineering investigations and design, Xi'an 710003, China
电磁法是一种广泛应用于矿产资源勘查、水文地质和环境地质调查等的地球物理勘探方法,依据响应性质可分为频率域电磁法和时间域电磁法.瞬变电磁法(Transient Electromagnetic Method)属于时间域电磁法,经过60多年的发展,其在理论研究和应用水平方面均取得了较大进步(薛国强等, 2007,2008;闫述等,2011).但由于多维正反演耗时久、对硬件要求高,因此前人研究不多,野外数据资料的解释仍停留在一维水平(熊彬和罗延钟,2006).2.5维问题,与三维相比较,大大减少了计算量,与纯二维比较又能更接近野外实际地质情况.
对于瞬变电磁法高维正演,常采用的方法为积分方程法( San Filipo and Hohmann, 1985;Xiong,1992)、有限单元法(Sugeng et al., 1993; Sugeng,1998;王华军和罗延钟,2003;熊彬,2005;周俊杰,2011)和时域有限差分法(Oristaglio and Hohmann, 1984;Adhidjaja and Hohmann, 1989;Leppin,1992;Wang and Hohmann, 1993;闫述等, 2001,2002;岳建华等,2007;闫述等,2009).积分方程法主要适用于三维正演且只适合于简单模型,这种算法首先频率域内利用基于张量格林函数的体积分方程法计算电磁场各分量的频率域响应,之后利用快速数字滤波技术将计算结果转换到时间域;有限单元法主要是在频率域中进行异常场的求解,之后通过傅氏变换转换到时间域,这种方法适用于二维、三维、2.5维问题,但理论较有限差分法复杂;时域有限差分法直接把含时间变量的Maxwell旋度方程或波动方程(扩散方程),在Yee氏网格或其他离散网格中转换成差分方程.每个网格点上的场值均与其相邻的场值有关.在每个时间步计算网格空间各点上的场值,随着时间的推进,便能直接模拟电磁波的传播及其与物体的相互作用.由于时域有限差分法的直接出发点是概括电磁场普遍规律的麦克斯韦方程,因此这一方法具有广泛的适用性.在时间域直接求解,避免了更多数学工具的使用,使得该算法简单易于实现(王长清和祝西里,1994),且能够直观的反应瞬变场随时间的扩散情况,因此在瞬变电磁的二维、三维正演中得到了广泛的应用.本文尝试利用有限差分方法进行瞬变电磁法2.5维正演模拟,通过与解析解的对比,证明了算法的正确性与可靠性.
1 差分方程 1.1 控制方程瞬变电磁场在各项同性的三维无源介质中近似为扩散方程

在直角坐标系中磁场强度各分量同样满足上述扩散方程,有

式中μ,σ分别为地下介质的磁导率与电导率,Hz为磁场强度垂直分量.
瞬变电磁法观测的数据主要为垂直感应电动势,可通过磁场对时间的导数来进行求解
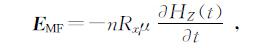
式中 E MF为感应电动势,μ为磁导率,n为接收线圈匝数,Rx为接收线圈的面积.因此瞬变电磁法2.5维正演将从(2)式出发.假设地下介质的电导率沿y方向均匀分布,则地下介质为二维结构,而场源为三维场源,则利用傅里叶变换可以将三维问题转换为二维问题.现引入如下傅氏变换
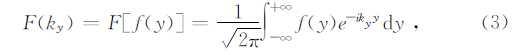
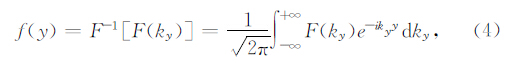
将式中磁场强度沿y方向做傅氏变换可以得到
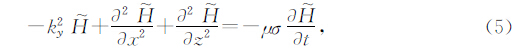
为了简单起见,上式和下文将用H来表示磁场的垂直分量Hz,上标波浪线表示波数域场值.
1.2 网格离散及Dufort-Frankel差分方程的推导2.5维有限差分问题中,空间网格的离散与二维相同,只是图中磁场值表示的是波数域的磁场值.如图 1,下标(i,j)表示网格点的空间坐标,σi,j表示各单元内的电导率值.Δx和Δz为网格空间步长,即Δxi=xi+1-xi,Δzj=zj+1-zj,Δt为时间步长,n为时间步长的个数,则Δtn=tn+1-tn.
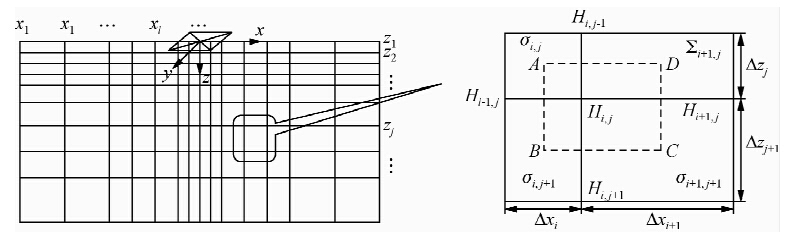 | 图 1 2.5维模型网格离散及波数域Hz分布 Fig. 1 Grid discretization of 2.5-D model and the distribution of Hz in wavenumber domain |
空间项的离散,对矩形ABCD积分并应用格林定理得
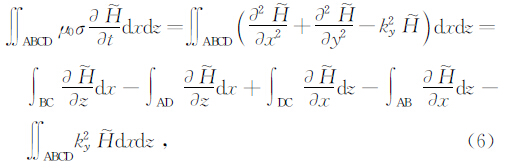
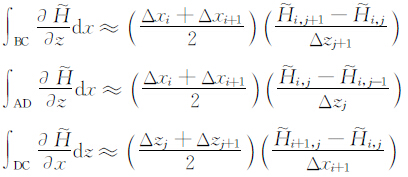
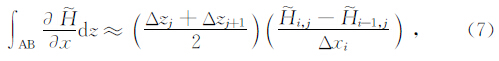
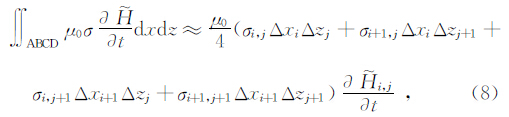
其中σ i,j为(xi,zj)节点周围四个单元电导率的面积加权平均值,即
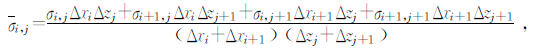
对时间导数的最简单近似为t=nΔt和t= n+1 Δt两个时刻的向前差分,即

这样利用(7)(8)和(9)式便可以推导出均匀网格情况下,按时间向前推算扩散方程的显示欧拉方法,即
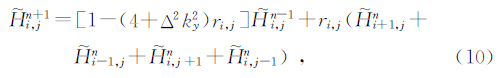
其中ri,j= Δt μσ i,jΔ2,称为局部网度.
不难证明当网度或小于1/(4+Δ2k2y)时,欧拉法是稳定的(米萨克N纳比吉安等,1992).故对于欧拉法最大的时间步长为

其中min(σ i,j)表示加权平均电导率的最小值.
针对不同的电导率,电磁场的扩散情况也不同,这对欧拉法是一个难题.在一个典型的地电断面中,min(σ i,j)可能低到10-3 S/m.若网格大小为10 m,式给出的最大时间步长约为0.025 μs.
现考虑较利用具有更高精度的中心差分来离散时间导数

此外利用如下近似

最终得磁场的差分格式如下
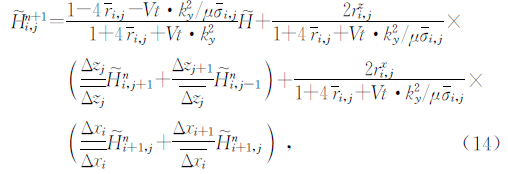
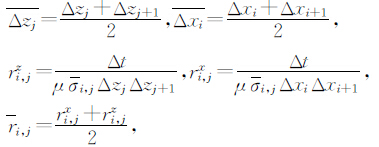
应用Dufort-Frankel法得到差分格式(14)是对任何时间步长无条件稳定的显示差分格式.Oristaglio and Hohmann(1984)给出的最大实用时间步长为
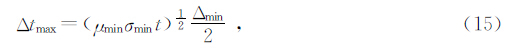
在电磁法模拟中取t=0.1 ms较为合理,因为它是大多数瞬变电磁系统开始记录的时间.当σmin为10-3 S/m,网格大小为10 m时,(15)式给出的最大时间步长为1.77 μs.
根据三维有限差分计算的经验将初始时间选取为(Oristaglio and Hohmann(1984))

其中μ和σ分别为地表的磁导率和电导率,Δ1为地表第一层的网格间隔.
2 初始条件本文采用矩形回线源作为激发源,将矩形回线源在均匀半空间上形成的波数域瞬变电磁场作为TEM2.5维有限差分正演模拟的初始条件.均匀半空间上空矩形回线源形成的拉氏域波数域垂直磁场表达式为(王华军和罗延钟,2003;周俊杰,2011)
空气层(z≤z0)中
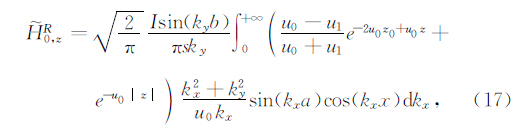
地下介质层(z>z0)中
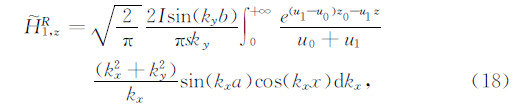
在勘查地球物理中,观测的是负阶跃函数的响应,及观测稳定电流切断后场的衰减,负阶跃响应可以表示为(米萨克N纳比吉安,1992)
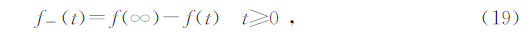
因此将所求的的频率域的响应通过逆拉氏变换到时间域,得到上阶跃电流的时间域响应,然后再利用(19)式来求取所需要的下阶跃响应.
2.1 正余弦变换(17)及(18)计算式中含有正余弦项,王华军(2004)运用成熟的汉克尔变换理论导出了正余弦变换的数值滤波法,并给出了250点的滤波系数,并详细分析了该方法的计算精度.其表达式为
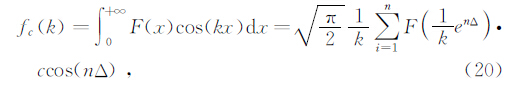
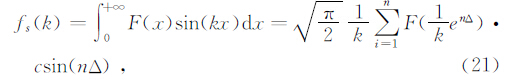
式中Δ为采样间隔,x为波数域变量,ccos(nΔ)、csin(nΔ)分别为为第n个余弦变换和正弦变换滤波系数.
2.2 逆拉氏变换逆拉氏变换的数值实现有多种办法,本文采用Gaver Stehfest(G-S)变换(罗延钟和昌彦君,2000).假设拉氏空间中的象函数为F(s),实空间的象原函数为f(t),则拉氏变换的表达式为
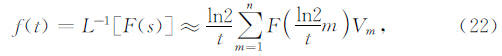
式中s为拉氏域变量,t为时间域变量,N为系数个数,Vm为GS变换系数
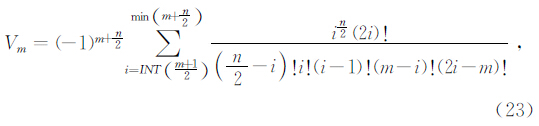
式中INT为取整函数,min为极小值函数.
本文根据前人的经验在计算中取n=12或n=16(周俊杰,2011).
2.3 反傅氏变换及波数的选取运用基于三次样条差值的反傅氏变换,对于反傅氏变换公式,三次样条插值法求取的公式及步骤如下(徐士良,1995):
设已知的函数为y=f(x),在给定的节点处x1
hj=xj+1-xj,j=1,2,…,n-1
aj=hj-1/(hj-1+hj),j=2,3,…,n-1
βj=3(1-aj)(yj-yj-1)/hj-1+aj(yj+1-yj)/hj,j=2,3,…,n-1
aj=-aj/ 2+(1-aj)aj-1,j=2,3,…,n-1
bj= βj-(1-aj)bj-1 / 2+(1-aj)aj-1,j=2,3,…,n-1
y′(xj)=ajy′(xj+1)+bj,j=n…1,n-2,…,2
利用数值导数y′(xi)(i=1,2,…,n),求解插值节点函数值公式为
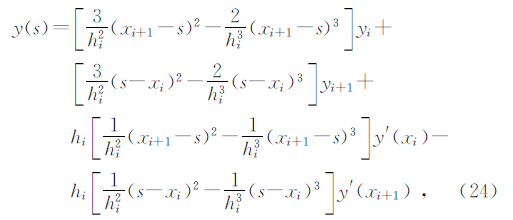
熊彬(2005)指出对于激发源为方形大回线源的地面瞬变电磁响应,波数的选取方法是在一定的波数变化范围(10-7~1.0)内每一个十进位间按对数间隔取三到四个波数,这样便能够使傅氏反变换的数值积分稳定、可靠.针对本文算法,采用同样的波数选取方法,综合考虑计算时间和计算精度,最终在10-5~10-1范围内等对数间隔选取17个波数进行计算.
在地下边界中,简单的假设位于边界上的波数域场量为零.这样做的前提条件是网格剖分要足够大,边界离源足够远(Oristaglio and Hohmann, 1984;Adhidjaja and Hohmann, 1989;Leppin,1992;Wang and Hohmann, 1993)
3.2 地-空边界条件已知在似稳条件下,自由空间的磁感应强度满足拉普拉斯方程
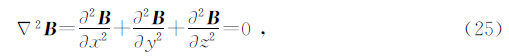
对于所研究的2.5维问题,经过傅氏变换,(25)式在波数域中变为Helmholtz方程
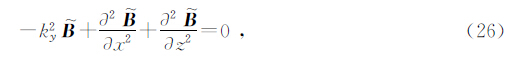
各分量可表示为
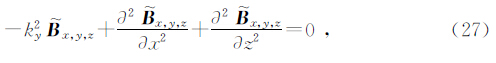
在求上式各分量的解的过程中规定x有界,而z趋向于无限大.且地空边界处的磁场值 B ~和磁场的导数 B ~ /z已知.上述亥姆赫兹方程的解的一部分可表示为可用观测点 x0,z0 对数奇异(Leppin,1992)
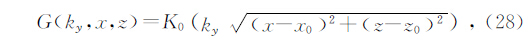
其中K0为第二类0阶虚宗量贝塞尔函数.根据格林定理,有
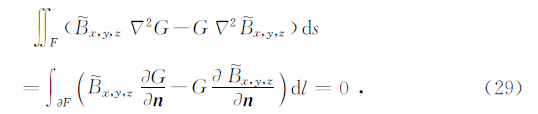
其中F为区域F的边界,但不包括围绕观测点的一个小圆环,法向量 n 垂直F指向外,积分路径如图 2.
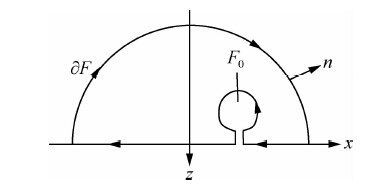 | 图 2 积分路径图 Fig. 2 Integral path |
对于Neuman问题,即地表处(z=0)磁场的导数 B ~ /z已知,此时定义格林函数形式为
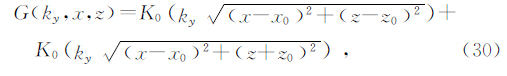
则 G z =0.将图中积分路径的上半部分置于无穷远,则格林公式为
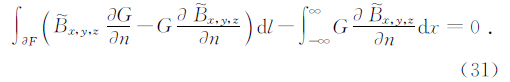
如果F0的半径足够小,则上式中此边界上的积分项中的G为-ln kyρ +K0 2ky z0,而G/ n 为1/ρ,dl为ρdφ.因ρ→0,则由上式可以得到计算地面以上部分磁场值的公式
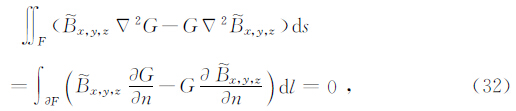
而对于Dirichlet问题,即在地表处已知,此时格林函数定义为
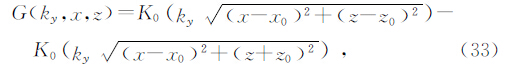
则G=0,且
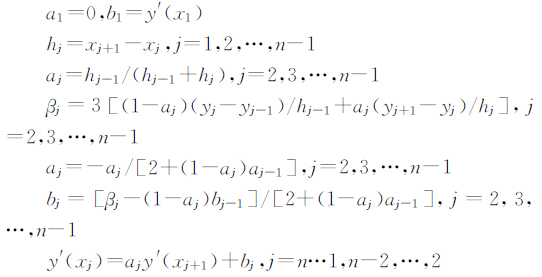
其中K0为第二类0阶虚宗量贝塞尔函数,根据格林定理,最终得到
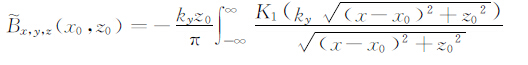

在有限差分计算过程中,已知地表的垂直磁场,利用(34)式便可以求出地表上空一个网格处磁场的垂直分量,进而进行差分迭代.
3.3 向上延拓的求解在计算中采用均匀磁导率μ0,因此以上延拓公式均适用于磁场强度各分量Hx,Hy,Hz.上述积分式中包含的零阶和一阶修正的贝塞尔函数,其求解方法数学上已有大量的研究,本文直接采用其近似表达式(石庆冬,2001).
对于式中无穷积分的求取,我们采用下述处理方法(李世健,2012)
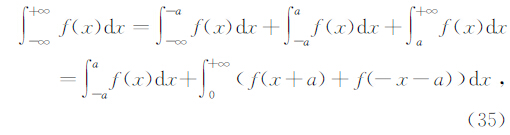
上式中第一部分的有限积分选择高斯-勒让德积分进行求解.又根据高-勒让德积分区间不能过大的性质,将大区间积分改成多个小区间积分之和,即
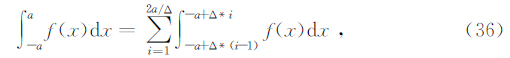
而第二部分采用高斯—拉盖尔积分进行求解.计算表明Δ和a这两个参数的选取直接影响着最终的计算精度和速度,综合考虑二者相互制约的特性,并通过大量的试算比较,计算中给定Δ=5,a=500-3000.
4 2.5-D数值模拟结果分析以上介绍了瞬变电磁法2.5维有限差分正演模拟的理论基础.利用Fortran语言编写了瞬变电磁法2.5维有限差分正演程序,现对数值模拟结果进行分析.
4.1 2.5-D正演结果验证 4.1.1 均匀半空间模型均匀半空间电阻率为100 Ωm,方形发射回线边长60 m,接收线圈等效面积50 m2,供电电流1 A,采用中心回线测量.有限差分最小时间步长1×10-8,最大延迟时间为10 ms,波数选取17个.图 3a、b给出了两种非均匀剖分网格条件下有限差分数值解与解析解的对比曲线,图a中网格规模为181×80,最小网格2 m;图b中网格规模为109×55,最小网格5 m.图c为误差曲线可以看出数值解与解析解基本吻合,当最小网格为2 m时,在10-6~10-3s时间范围内最大相对误差不超过10%,10-3~10-2 s时间范围内最大相对误差为16%;当最小网格为5 m时,整体误差增加.当最小网格大小变化时对计算精度有所影响,且在时域有限差分计算中空间网格与时间步长的选取相互制约,影响着最终的计算精度.
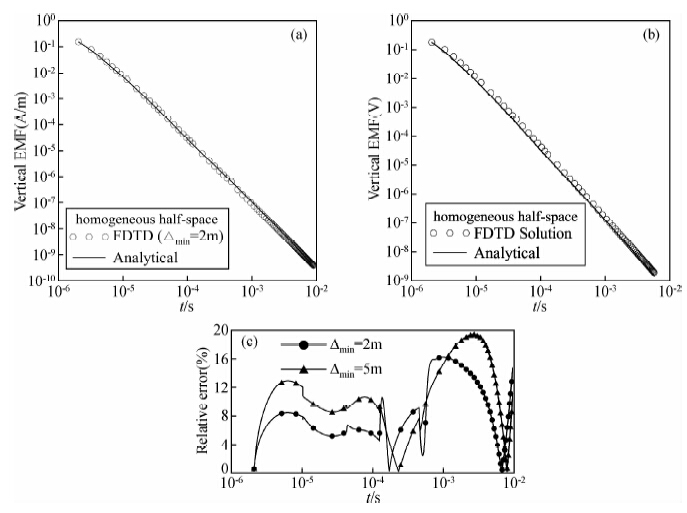 | 图 3 均匀半空间数值解与解析解对比(a)垂直感应电动势(Δmin=2 m);(b)垂直感应电动势(Δmin=5 m);(c)垂直感应电动势相对误差. Fig. 3 Comparison of analytical and numerical solutions for homogeneous half-space |
首先是电阻率分层均匀的H型三层地电模型,模型参数为:ρ1=100 Ωm、ρ2=10 Ωm、ρ3=100 Ωm;层厚度h1=100 m、h2=50 m,方形发射回线边长60 m,接收线圈等小面积50 m2,供电电流1 A,采用中心回线测量.有限差分网格规模181×80,最小网格2 m,最小时间步长1×10-8,最大延迟时间为10 ms,波数选取17个.图 4为感应电动势响应曲线,可以看出有限差分数值解与解析解基本吻合,在如图所示的10-6~10-2 s时间范围内,计算的相对最大相对误差为10.91%,最小相对误差为0.36%,平均相对误差为3.91%.
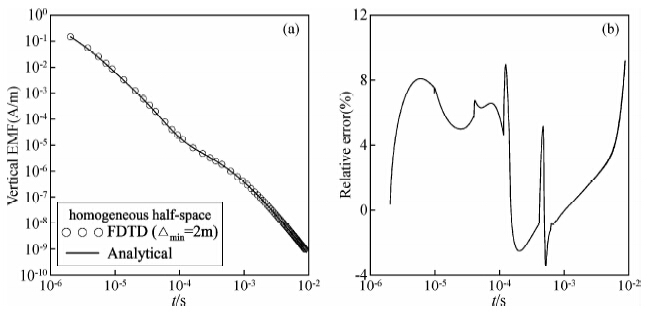 | 图 4 H型层状模型数值解与解析解对比(a)垂直感应电动势;(b)垂直感应电动势相对误差. Fig. 4 Comparison of analytical and numerical solutions for H-layered model |
接下来是K型三层地电模型,模型参数为:ρ1=100 Ωm、 ρ2=1000 Ωm、ρ3=100 Ωm;层厚度h1=100 m、h2=50 m,其他参数同上.图 5给出了感应电动曲线,可以看出有限差分数值解与1D数值解基本吻合,在如图所示的10-6~10-2 s时间范围内,计算的相对最大相对误差为15.80%,最小相对误差为0.0009%,平均相对误差为4.88%,可见K型模型计算精度较H型模型差.且可以看出瞬变电磁法对低阻体的反映较之高阻要好.
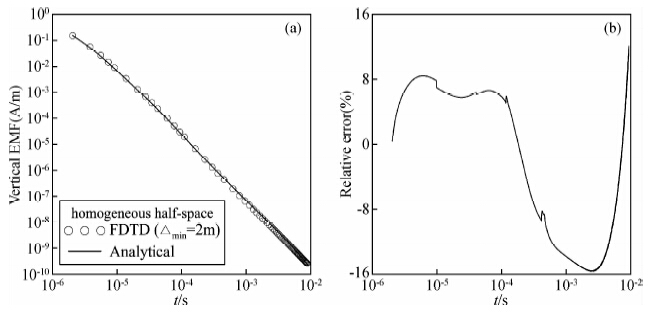 | 图 5 K型层状模型数值解与解析解对比(a)垂直感应电动势;(b)垂直感应电动势相对误差. Fig. 5 Comparison of analytical and numerical solutions for K-layered model |
误差来源分析:瞬变电磁法测量的感应电动势从早期到晚期跨越了八、九甚至更多个数量级,而且在时域有限差分法数值模拟中涉及到多个环节,各个环节误差积累.主要表现在:
(1)地空边界条件的处理中,插值与无穷积分的计算,引入误差,地下边界处场值设为0,计算区域有限,不能够真实体现场的传播特性,引入误差.
(2)均匀半空间的数值解本身存在误差,再作为有限差分计算的初始源,将误差带入,并随着时间的推进使误差叠加增大.
(3)反傅氏变换为无穷积分,我们只选取部分波数进行计算,带入误差.
(4)空间网格、时间步长的选取带来误差,当网格增大或时间步长增大时将严重影响最终的计算精度.
4.1.3 FDTD与FEM结果对比首先给出本文计算结果与周俊杰(2011)有限元结果的对比,计算中方形发射回线边长50 m,其他参数上文中H型层状模型相同.图 6a为有限元(FEM)数值解与1D解析解的对比曲线,b为有限差分(FDTD)数值解与1D解析解的对比曲线,c为二者与解析解相对误差曲线.图c中可以看出,两种方法在早期和中期均与解析解相吻合,而在10-3~10-2 s范围内本文有限差分计算明显优于文献中有限元方法结果.
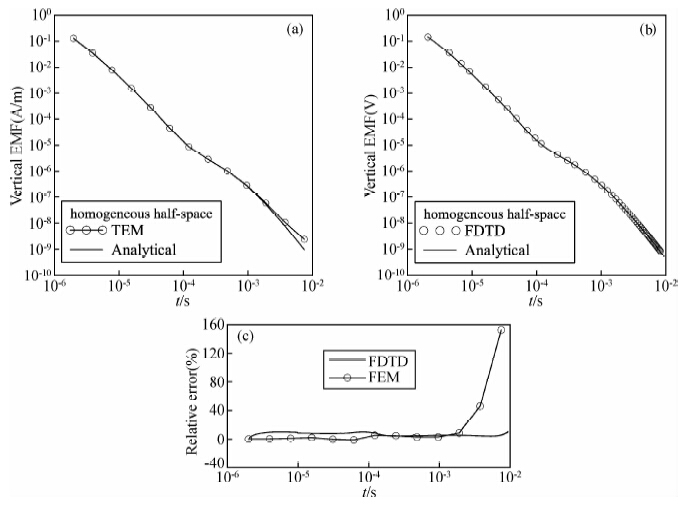 | 图 6 H型层状介质FEM与FDTD数值解与解析解的对比(a)FEM数值解与解析解对比;(b)FDTD数值解与解析解对比;(c)FDTD与FEM数值解与解析解相对误差. Fig. 6 Comparison of analytical and FEM and FDTD numerical solutions for H-layered model |
此外,熊彬和罗延钟(2006)有限元计算结果指出,对于H型模型,计算平均相对误差为-5%;K型层状模型平均相对误差为5%,本文计算误差与之相当,进一步证明本文计算的可靠性.
4.2 中心回线装置响应特征为了进一步验证程序的正确性,下面给出两个局部异常体模型中心回线装置剖面响应特征.图 7为模型一直立低阻板状体示意图.如图所示,围岩电阻率ρ0=100 Ωm,低阻直立板状体电阻率ρ1=1 Ωm,顶端埋深20 m,异常体垂向和横向延伸分别为100 m和20 m.测量装置为中心回线装置,方形发射回线边长50 m,接收线圈等效面积50 m2,供电电流1 A.
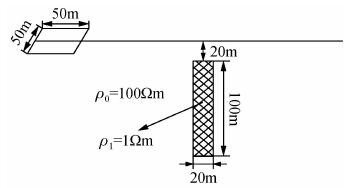 | 图 7 模型一示意图(中心回线装置) Fig. 7 Schematic diagram of model one(central loop unit) |
图 8给出了上述模型21个测深点的中心回线瞬变电磁响应.图中横轴为测深点位置,坐标原点位于异常体中心正上方,测深点位置关于坐标原点对称分布;纵轴为感应电动势,从上到下对应多个采样时间道上的响应.从图中可以看到,早期道异常表现为单峰异常,极大值出现在了异常体中心正上方,随着时间的延迟,异常表现为双峰异常,两个极大值出现在直立板两侧,而直立板上方出现极小值,在晚期到异常又表现为单峰异常,极大值出现在板状体中心正上方.异常响应特征物理模拟(牛之琏,1992)结果以及其他数值模拟结果(熊彬和罗延钟,2006)规律一致.
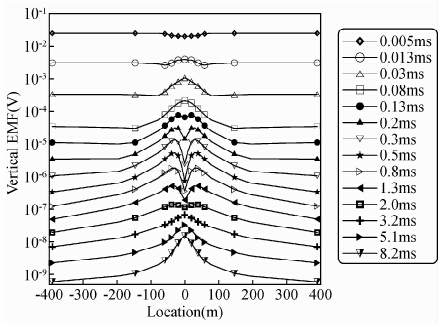 | 图 8 模型一瞬变电磁测深多测道剖面图 Fig. 8 Multi-chanel profile for TEM sounding of model one |
图 9为模型二双低阻体模型示意图,围岩电阻率ρ0=100 Ωm,等轴状低阻体电阻率分别为电阻率ρ1=1 Ωm,ρ2=10 Ωm,规模均为20 m×20 m,顶端埋深均为20 m,两异常体相距200 m.测量装置为中心回线装置,方形发射回线边长50 m,接收线圈等效面积50 m2,供电电流1 A.
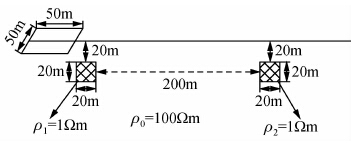 | 图 9 模型二示意图(中心回线装置) Fig. 9 Schematic diagram of model 2(central loop unit) |
图 10给出了测线方向28个测深点各采样时间道上的瞬变电磁场剖面响应曲线.平剖面测量中心点位于坐标原点,亦即量异常体中心位置.可以看到,在每个异常体上方表现出了异常特征,与板状体模型类似,早期到为单峰异常,之后变为双峰异常,最后又变为单峰异常吗,且在中期时间段,右侧异常体异常受到左侧较低组异常体的影响,单峰异常并未表现出对称形态.此外可以看出,电阻率相对较小的异常体的异常较大.这说明电磁场在低阻介质中扩散速度较慢;目标体(异常体)电阻率越低,瞬变电磁法的探测效果越好.
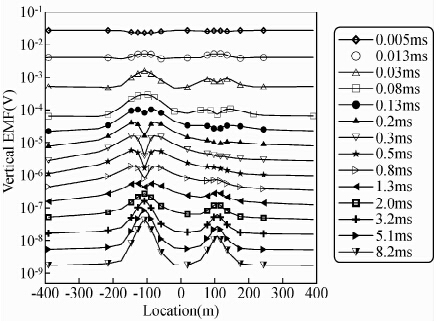 | 图 10 模型二瞬变电磁测深多测道剖面图 Fig. 10 Multi-chanel profile for TEM sounding of model two |
在瞬变电磁法二维有限差分正演模拟的基础上,展开了瞬变电磁法2.5维有限差分正演模拟研究.其中涉及到的关键问题一是波数域中的初始条件,二是波数域中边界条件的处理.
2.5D正演模拟中采用的是矩形回线源,只能推导出其在均匀半空间上形成的波数域、频率域瞬变电磁场表达式,之后利用正余弦变换、GS变换等数值计算方法得到波数域的瞬变场作为初始条件.
2.5D正演模拟中,地空边界条件扔采用向上严拓的方法.文中推导出了波数域的向上延拓公式.在计算中涉及到虚宗量贝塞尔函数的求解、无穷积分的处理、高斯勒让德积分、高斯拉盖尔积分、三次样条插值等,计算复杂、速度慢.
利用Fortran语言编写了瞬变电磁法2.5维有限差分正演程序,将FDTD数值模拟结果与均匀半空间模型、H型层状模型、K型层状模型的解析解进行了对比,曲线形态与解析解基本吻合,平均相对误差控制在5%以内,证明了算法的正确性与可靠性;将FDTD数值模拟结果与FEM数值模拟结果进行对比,在早期,FDTD比FEM计算结果稍差,而在晚期FDTD计算结果优于FEM计算结果;通过对两个简单模型的模拟,证明了算法的有效性.
致 谢 诚挚感谢强建科副教授、任政勇副教授在本文撰写中给予的亲切指导及宝贵意见.
| [1] | Adhidjaja J I and Hohmann G W.1989.A finite-difference algorithm for the transient electromagnetic response of a three dimensional body[J]. Geophysical Journal International, 98(2), 233-242. |
| [2] | Leppin M. 1992.Electromagnetic modeling of 3-D sources over 2-D inhomogeneities in the time domain[J]. Geophysics, 57 (8) : 994-1003. |
| [3] | Li S J. 2012.Numerical calculation of infinite integral[J]. Mathematics Learning and Research(in Chinese), 13:123-124. |
| [4] | Luo Y Z,Chang Y J.2000.A rapid algorithm for G-S transform[J]. Chinese J Geophys, 43(5): 684-690. |
| [5] | Nabighian M N.1992.Electromagnetic methods in applied geophysics(Vol. 1, Theory) (in Chinese) [M].Translated by ZHAO Jingxiang and WANG Yanjun,Beijing: Geological Publishing House. |
| [6] | Niu Z L.1992.Principle of Time domain Electromagnetic Method(in Chinese)(M).Changsha:Central South University of Technology Press. |
| [7] | Oristaglio M L and Hohmann G W. 1984. Diffusion of electromagnetic fields into a two-dimensional earth:A finite-difference approach[J].Geophysics, 49 (7) : 870-894. |
| [8] | San Filipo W A and Hohmann G W.1985. Integral equation solution for the transient electromagnetic response of a three-dimensional body in a conductive half-space[J]. Geophysics, 50(5): 798-809. |
| [9] | Shi Q D. 2001. Numerical computation of modified Bessel functions for integer orders and complex arguments[J].Jour nal of Jiaozuo I nstitute of T echnolog y ( Natural Science) (in Chinese), 20(2):101-104. |
| [10] | Sugeng F, Raiche A, Rijo L. 1993. Comparing the time-domain EM response of 2-D and elongated 3-D conductors excited by a rectangular loop source[J]. Journal of Geomagnetism and Geoelectricity, 45(9): 873-885. |
| [11] | Sugeng F. 1998. Modeling the 3D TDEM response using the 3D full-domain finite element method based on the hexahedral edge-element technique[J]. Exploration Geophysics, 29(4): 612-619. |
| [12] | Wang C Q,ZHU Xili.1994. The finite difference time domain methods for electromagnetics(in Chinese) [M].Beijing:PEKING University Press. |
| [13] | Wang H J,LUO Yanzhong. 2003.Algorithm of a 2.5 dimensional finite element method for transient electromagnetic with a central loop[J]. Chinese J Geophys(in Chinese), 46(6): 855-862. |
| [14] | Wang H J.2004.Digital filter algorithm of the sine and cosine transform[J]. Chinese Journal of Engineering Geophysics (in Chinese), 1(4):329-335. |
| [15] | Wang T and Hohmann G W. 1993.A finite-difference, time-domain solution for threedimensional electromagnetic modeling[J]. Geophysics, 58 (6) : 797-809. |
| [16] | Xiong B. 2005.Some problems on 2.5-D transient electromagnetic forward[J]. Computing Techniques for Geophysical and Geochemical Exploration(in Chinese), 28(2): 124-128. |
| [17] | Xiong B, LUO Y Z. 2006. Finite element modeling of 2.5-D TEM with block homogeneous conductivity[J]. Chinese J Geophys(in Chinese), 49(2): 590-597. |
| [18] | Xiong Z. 1992. Electromagnetic modelling of three-dimensional structures by the method of system iterations using integral equations[J]. Geophysics, 57(12): 1556-1561. |
| [19] | Xu S L. 1995. Arithmetic of fortran program(in Chinese)[M].Beijing:Tsinghua University Press. |
| [20] | Xue G Q,Li X,Di Q Y.2007.The progress of TEM in theory and aoolication[J].Progress in Geophys(in Chinese), 22(4):1195-1200. |
| [21] | Xue G Q, Li X,Di Q Y. 2008. Research progress in TEM forward modeling and inversion calculation. Progress in Geophys(in Chinese),23(4):1165-1172. |
| [22] | Yan S,Chen M S Fu J M. 2001.Time-domain behavior of transient electromagnetic field signal under ground and on the surface of the earth[J]. COAL GEOLOGY & EXPLORATION(in Chinese), 29(1):55-57. |
| [23] | Yan S, Chen M S Fu J M. 2002.Direct time-domain numerical analysis of transient electromagnetic fiflds[J]. Chinese J Geophys(in Chinese),45(2):275-284. |
| [24] | Yan S,Shi X X,Chen M S. 2009.The probing depth of transient electromagnetic field method[J]. Chinese J Geophys(in Chinese), 52(6): 1583-1591. |
| [25] | Yan S,Xue G Q,Chen M S. 2011. Review and perspective of the oretical study on large loop TEM response[J].Progress in Geophys(in Chinese), 26(3):941-947. |
| [26] | Yue J H,Yang H Y,Hu B. 2007. 3D finite difference time domain numerical simulation for TEM in-mine[J].Progress in Geophys(in Chinese), 22(4):1195-1200. |
| [27] | Zhou J J. 2011. Research on airborne transient electromagnetic 2.5-D forward modeling[D].ChangSha:Central South university. |
| [28] | 李世健. 2012.无穷积分的数值计算[J]. 数学学习与研究, 13:123-124. |
| [29] | 罗延钟, 昌彦君. 2000. G-S变换的快速算法[J]. 地球物理学报, 43(5): 684-690. |
| [30] | 米萨克N纳比吉安. 1992.勘查地球物理—电磁法(第一卷,理论) [M]. 赵经祥,王艳君译,北京:地质出版社. |
| [31] | 牛之琏.2007.时间域电磁法原理[M].长沙:中南大学出版社. |
| [32] | 石庆冬. 2001. 整数阶复宗量变形贝塞尔函数的计算[J].焦作工学院学报(自然科学版),20(2):101-104. |
| [33] | 王长清,祝西里. 1994.电磁场计算中的时域有限差分方法[M].北京:北京大学出版社. |
| [34] | 王华军, 罗延钟. 2003.中心回线瞬变电磁法2.5维有限单元算法[J]. 地球物理学报, 46(6): 855-862. |
| [35] | 王华军. 2004.正余弦变换的数值滤波算法[J].工程地球物理报, 1(4):329-335. |
| [36] | 熊彬. 2005. 关于瞬变电磁法2.5维正演中的几个问题[J]. 物探化探计算技术, 28(2):124-128. |
| [37] | 熊彬, 罗延钟. 2006. 电导率分块均匀的瞬变电磁2.5维有限元数值模拟[J].地球物理学报, 49(2): 590-597. |
| [38] | 徐士良.1995. FORTRAN常用算法程序集[M].北京:清华大学出版社. |
| [39] | 薛国强,李貅,底青云.2007.瞬变电磁法理论与应用研究进展[J].地球物理学进展,22(4):1195-1200. |
| [40] | 薛国强,李琳,底青云.2008.瞬变电磁法正反演问题研究进展[J].地球物理学进展, 23(4):1165-1172. |
| [41] | 闫述,陈明生,傅君眉. 2001.瞬变电磁场信号在地下的扩散及地面上的时域响应特性[J].煤田地质与勘探,29(1):55-57. |
| [42] | 闫述,陈明生,傅君眉.2002.瞬变电磁场的直接时域数值分析[J].地球物理学报, 45(2):275-284. |
| [43] | 闫述,石显新,陈明生. 2009.瞬变电磁法的探测深度问题[J]. 地球物理学报, 52(6): 1583-1591. |
| [44] | 闫述,薛国强,陈明生.2011.大回线源瞬变电磁响应理论研究回顾及展望[J].地球物理学进展,26(3):941-947. |
| [45] | 岳建华,杨海燕,胡搏.2007.矿井瞬变电磁法三维时域有限差分数值模拟[J].地球物理学进展,22(6):1904-1909. |
| [46] | 周俊杰. 2011. 航空瞬变电磁法2.5维正演模拟研究[D][硕士论文].长沙:中南大学. |
 2014, Vol. 29
2014, Vol. 29

