2. 胜利测井公司, 东营 257096
2. Shengli Logging Company, Dongying 257096, China
声波测井的频率与岩芯测量的频率相差很大,两种方法所测量的声波时差有比较大的差别.目前采用的对穿式的测量方法频率很高(500 kHz~2 MHz),所测量的声波时差只能够近似满足用声波时差计算砂岩孔隙度的应用要求(Brown and Seifert, 1997;李铭等,1999;张元中等,2001;刘之的等,2003;王勇等,2006;杨默函等,2006;俞军等,2006).不能够满足日益增长的利用砂岩的声波时差随频率的变化曲线识别孔隙流体类型的应用要求(Jones,1986;胡恒山和王克协,2001;胡学红等,2004),需要新的测量岩芯声波时差的方法.另外,由于实验用岩芯的长度很短,对穿法测量时波形的起始点选择对时差测量结果影响很大.
《用穿透法测量声速时初始点的选择问题》(沈建国,2003)讨论了对穿方法中起始位置的选择和刻度方法.
《压电换能器和换能器阵》(栾桂东等,2005)在讨论压电材料的集中参数表示时曾经指出:通过测量压电片的共振频率和反共振频率可以获得压电片的声速.即压电片在自由状态下被正弦波电信号激发,当电信号的固有频率与压电片自身的固有频率相等时,压电片处于谐振状态,这时,其振动的波阻抗最小,在电参数上表现为其电导的实部取极大值.用阻抗分析仪测量该频率,便可以获得其纵波传播速度.这种测量方法依赖于阻抗分析仪,主要利用了压电片自身振动时所产生的固有频率,其关键是压电片自身振动时的固有频率与声速的关系.这种测量方法利用了声波在岩芯中多次反射、反复传播的过程,测量到的波形中包含了这些多次反射所携带的声速信息.
《High-Intensity Ultrasonics》(Abramov,1998)讨论了一维圆柱杆的振动模式,给出作为一维振动时所满足的长度与半径比的条件.《超声变幅杆的原理和设计》(林仲茂,1987)给出了有限长一维杆变直径时的振动特征,指出了在直径突变出其应力分布集中的结论.《应用声学基础》(沈建国,2005)、《压电测量》(张沛霖和张仲渊,1983)、《Vibration and Sonic》(PMM)、井孔的声场与波(张海澜,2004)、《定量测井声学》(唐晓明和郑传汉,2004)进一步给出了一维杆振动和声传播以及二维介质声波传播特征,指出了声速在振动过程和固有频率计算中的作用.《Velocity Dispersion:A Tool for Characterizing Reservoir》(Brown and Seifert, 1997)、《Pore fluids and frequency-dependent wave propagation》(Jones,1986)、《低孔隙度低渗透率砂岩的声波特性实验研究》(胡学红等,2004)、《应用地震纵横波速综合参数识别层序地层界面》(杨国臣等,2009)、《含油饱和度对纵波速度影响规律的实验研究》(李洁和李书光,2012)、《圆柱形共振腔中存在人工孔隙岩样的共振声谱实验测量》(丛健生等,2007)从不同的应用需要和测量方法讨论了砂岩速度对测量的意义(谭廷栋,1989;李长文等,2006;施斌全,2007).
1 对穿法岩芯测量存在的问题以往的岩芯声速测量方法是对穿法,在岩芯的两端分别放置一个发射探头和一个接收探头.从测量的波形中人工选择波形的起始点得到传播时间,减去发射探头和接收探头直接对接时的时间后,得到声波在岩芯中的传播时间.用岩芯长度除以所测量的传播时间得到岩芯的速度或者时差(沈建国等,2002;丛健生等,2007).上述测量过程有下列几个缺陷:(1)发射、接收探头对接时所测量的波形幅度很大,探头之间夹岩芯时,波形幅度减小,这两种不同幅度波形所获得的波形起始位置有差别,该差别给时差测量带来了误差.(2)当波形幅度很小时,需要对波形进行放大,放大器本身能够对波形带来微秒级的整体延迟,该延迟在探头对接时不存在.(3)换能器有响应时间,即当电脉冲激励换能器时,换能器需要一定的时间才能够激发出振动,同样,当换能器接收到振动以后,也需要一定的时间才能够将振动转换为电信号.这些响应时间包含在换能器对接时的时差中或者通过换能器对接的方法进行测量.(4)换能器对接时测量的时差还包含声波在换能器辐射面匹配层中的传播时间.(5)发射波形时,首波并不是波形中最大幅度的振动,而接收时,接收波形的最大幅度也不在首波的位置.这样,测量时差时没有用到波形的最大能量位置,没有发挥出声波波形固有的特征.
以上是对穿法测量岩芯声速的固有缺陷,是方法本身所带来的(宋立军等,2005).在选择测量波形起始点时,人为因素的影响更是无法记录和克服,导致同一个岩芯,不同的人测量会得到不同的声速值.
上述测量方法仅仅利用了声波在岩芯中一次传播的传播时间,所测量的信号中,仅仅利用了首波的到达时刻,大量的后续波信息没有被利用.为了提高声波时差的测量精度(朱留方和沈建国,2004),通常采用增加频率的方法.
2 新测量方法的理论依据传统的对穿法是瞬态测量方法,主要利用了声波在岩芯中的传播时间.即通过测量声振动在该岩芯中的传播时间来获得岩芯的纵波速度.该测量方法要求岩芯长度最少要大于波长的5倍.这样,当岩芯比较短时,换能器激发振动的频率就比较高,相应地接收波形的频率也比较高.为了提高测量精度,选择换能器的谐振频率发射以增加发射能量;同样,也选择接收换能器的谐振频率接收以获得比较大的波形幅度.
当激发频率比较高时,换能器中的声-电或者电-声转换器件的厚度就比较薄,其发射振动的能量就比较小.
新的岩芯声波时差测量方法则采用大功率冲击的激发方式,在岩芯的一端激发出各种频率的振动,这些振动在岩芯中传播后,在两端被多次反射,最后,由岩芯两端的自由边界条件决定能够在有限长岩芯内部传播的声波频率——岩芯的固有频率.这些频率的振动幅度大,周期多,波形接近于正弦波,容易测量.
新方法主要测量振动稳定以后波形中幅度比较大的后续波,实现起来比较容易.原始测量波形幅度大,周期多,固称为振动测量方法或者稳态测量方法.该方法通过所测量的固有频率得到声波速度,有效地克服了上述对穿法测量存在的缺陷.
图 1所示为所测量的圆柱岩芯,设其长度为l,长度与直径比大于1.6,满足一维杆振动条件.设位移U=Asinkz+Bcoskz,根据胡克定律,应力F为
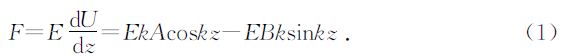
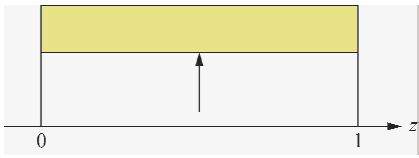 | 图 1 圆柱岩芯 Fig. 1 Circular column of core |
将岩芯从中间支起,两边自由,则两端的应力为0,将z=0和z=l时应力为0的边界条件分别代人(1)式得到:A=0和sinkl=0.将波数k与岩芯的纵波速度v以及振动的频率f之间的关系代人得到:
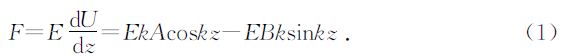
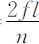 取n=1,则有
取n=1,则有

从上式可以看到:只要测量到了有限长岩芯的谐振频率即可获得岩芯的纵波速度(3)式.
上述新的测量方法利用了声波在岩芯中的多次传播特征,即利用声波在两端自由界面上多次反射以后形成的谐振状态实现对岩芯纵波速度的测量.测量时,岩芯处于谐振状态,以其自身的固有频率振动,振动幅度比较大.因此,对测量换能器的要求比较低.用普通的加速度计即能够有效记录波形.振动特性的激发也比较容易,采用敲击或者用专用锤敲击即可.
由于所测量的接近稳态的后续波中包含了岩芯纵波速度的信息,在频率分析中充分利用了这些信息,因此,测量方法较传统的穿透方法简单.或者说新方法主要用后续波实现了对岩芯纵波速度的测量.
3 实际测量结果及分析为了证明新方法的有效性,我们截取了直径分别为30 mm和32 mm的铝棒和不锈钢棒,为了简单,棒的长度选择了0.5 m,这样,由(3)式知道,所测量的频率即为材料的纵波速度v.实心铝棒和不锈钢棒不具有频散特征,其速度是常数.
在不锈钢棒的一端贴上压电片,直接敲击压电片获得的波形如图 2左图所示,其中,幅度最大的脉冲波形是敲击时的冲击波,脉冲宽度与敲击方式有关.脉冲过后幅度比较小的波形振动周期很多,接近于稳态,是棒谐振时的振动波形,该波形是我们所需要的原始测量波形,对这些波形进行FFT处理,获得如图 2右图所示的频谱,其中最大峰值位置4877.1 kHz即为所测量波形的谐振频率.由(3)式知道:该谐振频率也即为不锈钢棒的纵波传播速度v(4877.1 m/s).另外,用锤击直接敲击铝棒,还可以产生二倍频的高频成分,在9754.3 kHz位置.用二倍频也可以计算棒的声速,这时需要对其谐振频率除以2.该速度测量值在不锈钢理论值的区间范围内.
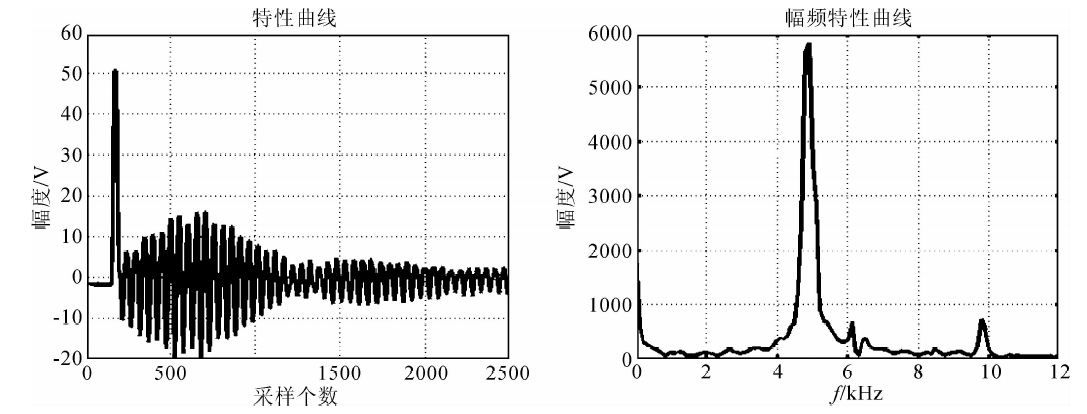 | 图 2 直接敲击不锈钢棒上的压电片获得的波形及其对应的频谱 Fig. 2 Waves detected after directly impacting the piezoelectric ceramics on aluminium bar and its corresponding frequency spectrogram |
从图上可以看到:在6.1 kHz位置,频谱曲线还有一个峰值.该峰值所对应的频率与(3)式刻画的振动模式不同,是由于敲击时棒的中间支起所致,不能够用于声速计算.
图 3是用硬铝棒测量的后续波形及其频谱.在5 kHz位置,频谱曲线上有一个幅度很大的峰值.该频率是铝棒的固有频率,用该频率得到铝棒的声速为5000 m/s,与硬铝的理论值5150 m/s接近.
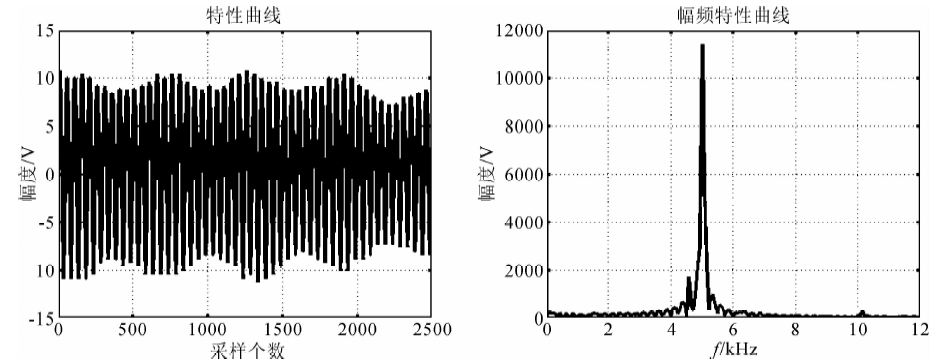 | 图 3 直接敲击铝棒上的压电片时所测量的后续波形及其对应的频谱 Fig. 3 The follow-up waves detected after directly impacting the piezoelectric ceramics on stainless steel bar and its corresponding frequency spectrogram |
从上述两个实际样品测量结果可以看出:实际的材料加工完成以后,其声速是固定的.由于加工工艺等因素的影响,与理论值之间会有一点差别.
4 注意事项(1)两端的加速度计体积要尽量小、重量要尽量轻,与岩芯断面的接触面要小,尽量不破坏自由边界条件.
(2)敲击时,要尽量快,避免多次接触.
(3)波形采集时,要尽量避开敲击时的波形,尽可能多地接收后续稳定的波形.
(4)波形采集长度要尽可能地长,波形越长,其做FFT后,频谱的采样间距越短,频率的分辨率越高.波形处理时,为了提高峰值处频率位置的精度.通常在波形的后面补0,补0越多,频率步长越小,频谱峰值位置越精确,即所测量的声波时差精度越高.
(5)岩芯长度与直径的比要大于1.6.为此可以用小直径的取样器取样.
(6)可以在岩芯端面上粘接多个加速度计进行多次测量.
(7)两个端面不能够接触固体,更不能够接地.岩芯侧面也不要接地,最好用小的支点将岩芯支起来,也可以用绳子将岩芯吊起来.支点位置最好选择在岩芯的中点,这里的振动位移为0,不影响测量.
(8)敲击方式不同,在测量波形中有时会出现低频模式,这是岩芯的弯曲振动模式,其固有频率与纵向振动的固有频率相差比较远,不会影响声速测量.
5 分析与讨论在岩芯的两个端面,用加速度计接收的是端面的振动加速度,也可以用位移或者速度计测量端面的振动位移与振动速度.这些振动的频率是由岩芯长度和岩芯的纵波传播速度决定的.因为岩芯两端的自由边界条件满足时,岩芯长度是半个波长的整数倍,而波长与频率、岩芯的纵波传播速度有关,所以,当岩芯及其长度确定后,其振动频率也随之确定.在岩芯的任意一点,其振动位移均按照该频率振动,随时间按照正弦(位移是余弦)规律变化.
从公式(2)知道:除了基频外,还有整数倍的倍频也满足边界条件.这意味着这些频率在实际测量波形中也能够存在.即所测量的波形是由基频及其整倍数的频率成分叠加而成的.具体能够激发出什么频率,与激发条件有关.用橡皮包裹的榔头敲击,产生的频率比较低,主要是基频;用铁榔头快速敲击,产生的频率比较高,这样,接收到的波形含倍频成分.
与传统的岩芯声速测量方法不同,本文提供的测量方法用大功率冲击,将岩芯自身的固有频率激发出来,使岩芯处于谐振状态.当岩芯声速比较高、弹性比较好、内部物理衰减比较小时,所测量的波形振动周期多,用这样的后续振动波形测量频率,其精度比较高.
本测量方法不测量波形幅度,更不用选择波形的起始点,测量过程中人为因素的影响降至最小.
如果采集波形的时间足够长,波形幅度随时间的总体衰减规律也能够测量到,则根据波动方程的解,还可以求出刻画介质的物理衰减特征的物理衰减系数.
对于声速随频率变化的砂岩岩芯,可以通过制作不同长度的岩芯样品来测量不同频率的声速.因为岩芯长度不同,其谐振频率不一样,岩芯谐振时,主要以其单个基频或者倍频的频率振动,不受岩芯频散(传播速度随频率改变)的影响.
图 4是石油工业常见的几种岩石的谐振频率与岩芯长度之间的关系.对于砂岩储集层来讲,取岩芯样品的长度为80 mm即可测量到频率为20~30 kHz的声速.这个条件用现有的钻井取芯横向(水平方向)取样即可满足.如果测量更低频率的声速,可以采用纵向(深度方向,沿钻井取芯方向)取样的方法从钻井取芯中取样.
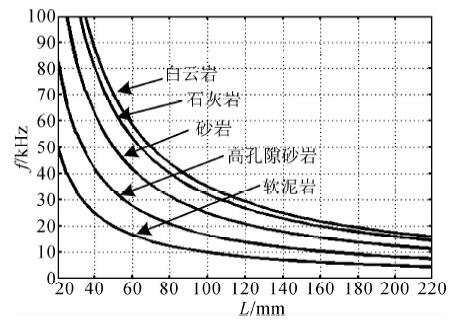 | 图 4 石油工业常见的几种岩石的谐振频率与岩芯长度之间的关系 Fig. 4 Relationship between the length of core and resonance frequency of several common seen rock in oil industry |
本方法还可以进一步延伸到液体中,即岩芯完全浸没在液体中时,根据一维杆中声波的传播特征:在其固有频率处其透射系数有极大值,并且远远大于其它频率.在液体中测量时可以用液体进行耦合,选择其它类型的换能器,选择稳态的激励方式.同样,也通过测量其谐振频率获得其声速.但是,与空气中测量不同,在液体中测量时可以获得其孔隙内饱和不同液体时的声速,例如测量砂岩岩芯在饱和水或者饱和油时的声速以及频散曲线.
6 结 论本文针对现有岩芯测量存在的问题,利用有限长岩芯自身固有频率的振动特征设计了岩芯纵波速度测量方法.该方法充分利用了岩芯自身振动所携带的声速信息,简化了测量过程.通过测量有限长岩芯的固有频率获得其纵波速度,有效地克服了传统测量方法中的缺点,纵波速度的测量精度比较高.通过改变岩芯长度可以测量不同频率的纵波速度,提供了岩芯频散曲线的测量方法.该方法还可以在液体中实施,为测量岩芯饱和液体时的声速提供了新的手段.测量声速时选择的频率与现有的声波测井频率一致,所测量的声速可以与声波测井的声速对比分析,有利于研究声波测井频率段岩芯的声波传播特征,为进一步利用声波测井信息研究孔隙流体类型提供了具体的措施和手段.
致 谢 感谢哈尔滨工业大学力学教研室赵树山教授提供的帮助.| [1] | Abramov O V. 1998. High-Intensity Ultrasonics[M]. Moscow, Russia: Gordon and Breach Science Publishers. |
| [2] | Brown R L, Seifert D. 1997. Velocity dispersion: a tool for characterizing reservoir[J]. Geophysics, 62(2): 477-486. |
| [3] | Cong J S, Wang X M, Xu D L, et al. 2007. Measurements of acoustic resonance spectroscopy for an oil filled cylinder cavity with samples[J]. Chinese Science Bulletin (in Chinese), 52(21): 2564-2568. |
| [4] | Hu H S, Wang K X. 2001. Dynamic permeability in poroelastic medium acoustic[J]. Chinese Journal of Geophysics (in Chinese), 44(1): 135-141. |
| [5] | Hu X H, Li C W, Li X, et al. 2004. Experiments on acoustic characters of low porous and permeable sandstones[J]. Well Logging Technology (in Chinese), 28(4): 273-276. |
| [6] | Jones T D. 1986. Pore fluids and frequency-dependent wave propagation[J]. Geophysics, 51(10): 1939-1953. |
| [7] | Li C W, Qiang Y M, Li G L, et al. 2006. Characteristics of modern acoustic logging technology development[J]. Well Logging Technology (in Chinese), 30(2): 101-104. |
| [8] | Li M, Lu Y Z, Zhang Y. 1999. An experimental study on acoustic parameters of low porous and permeable rock[J]. Petroleum Geology & Oilfield Development in Daqing (in Chinese), 18(5): 42-45. |
| [9] | Lin Z M. 1987. Principle and Design of Ultrasonic Amplitude Transformer (in Chinese) [M]. Beijing: Science Press. |
| [10] | Liu Z D, Xia H Q, Chen F X, et al. 2003. Causes leading to errors in core electricity experiments and their corrections[J]. Well Logging Technology (in Chinese), 27(4): 274-277. |
| [11] | Luan G D, Zhang J Y, Wang R Q, et al. 2005. Piezoelectric Transducer and Array (in Chinese) [M]. Beijing: Peking University Press. |
| [12] | Molyneux J B, Schmitt D R. 1999. First-break timing: arrival times by direct correction[J]. Geophysics, 64: 1492-1501. |
| [13] | Shen J G, Chen Y, Yuan F W, et al. 2002. The calculation of P- and S-wave velocities from acoustic waveform logs with only two receivers in different ranges[J]. Geophysical Prospecting for Petroleum (in Chinese), 41(1): 115-120. |
| [14] | Shen J G. 2005. Foundation of Applied Acoustics (in Chinese) [M]. Tianjin: Tianjin University Press. |
| [15] | Shen J G. 2003. Selection of first-break timing in using transmitting method for measuring sonic velocity[J]. Oil Geophysical Prospecting (in Chinese), 38(1): 44-47. |
| [16] | Song L J, Ma J, Wang K X, et al. 2005. The numerical simulation and analysis on the head waves modes and full waveform in borehole [J]. Journal of Northeast Normal University (in Chinese), 37(2): 50-54. |
| [17] | Tang X M, Zheng C H. 2004. Quantitative Logging Acoustic (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [18] | Tan T D. 1989. A method for indicating gas-bearing sand formation with the use of head P wave amplitude[J]. Oil Geophysical Prospecting (in Chinese), 24(4): 422-430. |
| [19] | Wang Y, Zhang C G, Li J F, et al. 2006. Study on influencing factors of lithological-electrical parameters[J].Journal of Oil and Gas Technology (in Chinese), 28(4): 75-77. |
| [20] | Yang M H, Shi G, Zhang Z B. 2006. Technique of laboratory measurements of electrical resistivity in sand stone at reservoir conditions[J]. Acta Scientiarum Naturalium Universitatis Pekinensis (in Chinese), 42(6): 729-734. |
| [21] | Yu J, Geng X, Li X H. 2006. Improved rock resistivity measurement method in low permeable reservoir and its application[J]. Well Logging Technology (in Chinese), 30(5): 394-396. |
| [22] | Zhang H L. 2004. Acoustic Field and Wave of Borehole (in Chinese) [M]. Beijing: Science Press. |
| [23] | Zhang P L, Zhang Z Y. 1983. Piezo-Electric Measurement (in Chinese) [M]. Beijing: National Defence of Industry Press. |
| [24] | Zhang Y Z, Chu Z H, Li M, et al. 2001. An experimental study of acoustic dispersion of rock and extrapolation of the velocity[J]. Chinese J. Geophys. (in Chinese), 44(1): 103-111. |
| [25] | Zhu L F, Shen J G. 2004. The method processing the slowness of P- and S-wave from waveforms of array sonic logging[J]. Well Logging Technology (in Chinese), 28(5): 373-377. |
| [26] | Zuo Q S. 2000. Application and analysis of the equivalent electrical admittance about piezoelectric transducer[J]. Journal of Changzhou Institute of Technology (in Chinese), 13(2): 37-42. |
| [27] | 丛健生, 王秀明, 徐德龙,等. 2007. 圆柱形共振腔中存在人工孔隙岩样的共振声谱实验测量[J]. 科学通报, 52(21): 2564-2568. |
| [28] | 胡恒山, 王克协. 2001. 孔隙介质声学理论中的动态渗透率[J]. 地球物理学报, 44(1): 135-141. |
| [29] | 胡学红, 李长文, 李新,等. 2004. 低孔隙度低渗透率砂岩的声波特性实验研究[J]. 测井技术, 28(4): 273-276. |
| [30] | 李长文, 强毓明, 李国利,等. 2006. 现代声波测井技术发展的若干特点[J]. 测井技术, 30(2): 101-104. |
| [31] | 李铭, 卢颖忠, 张莹. 1999. 低孔低渗岩石声学参数的实验研究[J]. 大庆石油地质与开发, 18(5): 42-45. |
| [32] | 林仲茂. 1987. 超声变幅杆的原理和设计[M]. 北京: 科学出版社. |
| [33] | 刘之的, 夏宏泉, 陈福煊,等. 2003. 岩电实验过程中误差产生的原因及校正方法研究[J]. 测井技术, 27(4): 274-277. |
| [34] | 栾桂东, 张金铎, 王仁乾,等. 2005. 压电换能器和换能器阵[M]. 北京: 北京大学出版社. |
| [35] | 沈建国, 陈宇, 袁福文,等. 2002. 用两个不同源距的声波测井全波波形计算纵波和横波波速[J]. 石油物探, 41(1): 115-120. |
| [36] | 沈建国. 2005. 应用声学基础[M]. 天津: 天津大学出版社. |
| [37] | 沈建国. 2003. 用穿透法测量声速时初始点的选择问题[J]. 石油地球物理勘探, 38(1): 44-47. |
| [38] | 宋立军, 马俊, 王克协,等. 2005. 首波、模式波及井孔全波时域波列的数值模拟与分析[J]. 东北师大学报, 37(2): 50-54. |
| [39] | 唐晓明, 郑传汉. 2004. 定量测井声学[M]. 北京: 石油工业出版社. |
| [40] | 谭廷栋. 1989. 用纵波首波幅度识别砂岩气层的方法[J]. 石油地球物理勘探, 24(4): 422-430. |
| [41] | 王勇, 章成广, 李进福,等. 2006. 岩电参数影响因素研究[J]. 石油天然气学报, 28(4): 75-77. |
| [42] | 杨默函, 史謌, 张祖波. 2006. 储层条件下砂岩岩心驱替实验方法研究[J]. 北京大学学报(自然科学版), 42(6): 729-734. |
| [43] | 俞军, 耿昕, 李晓辉. 2006. 低渗透油藏岩电实验方法改进及应用效果[J]. 测井技术, 30(5): 394-396. |
| [44] | 张海澜. 2004. 井孔的声场和波[M]. 北京: 科学出版社. |
| [45] | 张沛霖, 张仲渊. 1983. 压电测量[M]. 北京: 北京国防工业出版社. |
| [46] | 张元中, 楚泽涵, 李铭,等. 2001. 岩石声频散的实验研究及声波速度的外推[J]. 地球物理学报, 44(1): 103-111. |
| [47] | 朱留方, 沈建国. 2004. 基于阵列声波测井波形二维谱分布的纵、横波时差处理方法[J]. 测井技术, 28(5): 373-377. |
| [48] | 左全生. 2000. 压电换能器的导纳分析及其应用[J]. 常州工学院学报, 13(2): 37-42. |
 2014, Vol. 29
2014, Vol. 29

