双侧向测井成本较低,应用广泛,是目前常规测井评价裂缝参数的首选方法(景建恩等,2003;刘春园等,2007;高霞等,2007;王晓畅等,2008;赵军龙等,2012).前人提出了一系列常见高阻基岩中双侧向测井裂缝参数评价模型( Van Golf-Racht,1982;Boyeldieu and Winchester, 1982;Sibbit and Faivre, 1985;Philippe and Roger,1990;李善军等,1996;李善军等,1997).A.M.Sibbit和O.Faiver研究了双侧向对不同角度裂缝的响应,归纳了双侧向幅度差随裂缝开度变化关系,提出了裂缝开度计算的Sibbit经典模型.黄烈林等人对该模型进行了改进(黄烈林等,2002).罗贞耀等人提出了任意视倾角的裂缝开度计算模型,可以计算倾斜裂缝开度,经过成像测井资料标定后计算精度相对较高(罗贞耀,1990; 张福明等,2010).李军等针对库车地区裂缝型砂岩储层提出了砂岩储层裂缝开度的计算方法,考虑了泥浆滤液侵入等因素的影响(李军等,2008).
然而以叙利亚生物灰岩为代表的低阻碳酸盐岩储层中,基岩电阻率低至1~5 Ωm.基岩与裂缝电阻率对比度低,双侧向响应受基质孔隙导电影响大,双侧向幅度差除受裂缝开度影响明显外,受裂缝视倾角,充填物电阻率,基岩电阻率等因素影响亦较大,常用裂缝评价模型往往针对于高阻裂缝型碳酸盐岩储层提出,在基质孔隙发育的低阻碳酸盐岩储层应用受限.
本文从三维有限元法出发,系统考虑基岩导电明显的碳酸盐岩储层中有限延伸的裂缝开度,角度,充填物、基岩电阻率等因素对双侧向测井响应的影响,正演不同裂缝参数下双侧向响应特征,进而从深(浅)侧向视电阻率在裂缝处变化率的角度提出不同角度下裂缝开度,孔隙度定量评价方法,为低阻碳酸盐岩储层裂缝参数评价提供了新的思路和方法.
1 双侧向数值模拟模型本文通过三维有限元法建立了低阻裂缝型储层柱状模型,其纵切面如图 1所示(灰色表示基岩,白色椭球表示裂缝,为了清晰的表示裂缝在模型中的分布,夸大了裂缝比例).接着采用四面体网格对求解域进行网格剖分.在裂缝、电极表面等几何尺寸、电场分布剧烈变化的区域采用边界层网格进行剖分,加密边界法向方向网格数,在远离边界的位置采用正常自由四面体网格剖分;并根据井中电场分布对电极表面、井筒、裂缝区域进行网格的加密处理,提升狭窄区域解析度,控制最大单元生成率已达到以减小误差,提高计算精度的目的.进而建立了具有335万网格的有限元模型.其中最小网格尺寸为31 μm,分布于裂缝与井轴交界面上;最大网格尺寸为7 m,位于模型外边界处.网格剖分如图 2所示.通过调整该模型参数,系统模拟了不同开度,角度,充填物、基岩电阻率裂缝的双侧向测井响应.
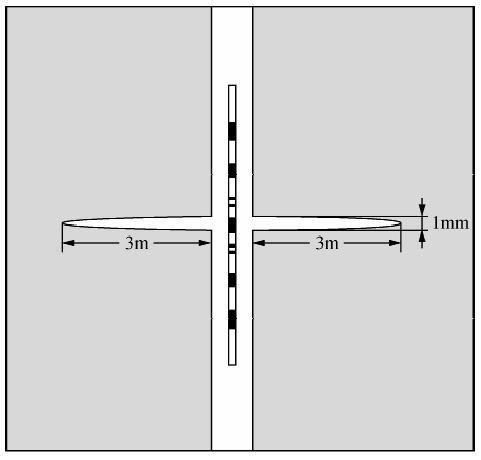 | 图 1 含水平裂缝的碳酸盐岩地层双侧向数值模拟模型示意图 Fig. 1 Schematic diagram of dual lateral log numerical simulation model of carbonate reservoir with horizontal fracture |
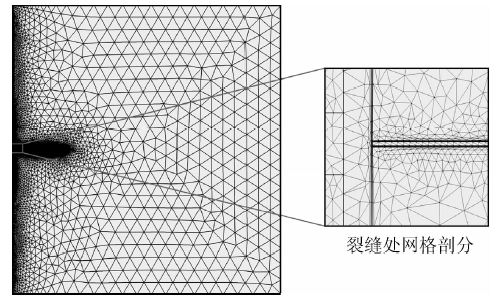 | 图 2 含水平裂缝的碳酸盐岩地层双侧向数值模拟模型有限元网格剖分示意图 Fig. 2 Schematic diagram of dual lateral log numerical simulation model mesh of carbonate reservoir with horizontal fracture |
模拟中采用拉普拉斯方程(Laplace's equation)模拟双侧向主电极(赵延文和聂在平,1998),屏蔽电极‘电流在地层介质中形成的电位场,柱坐标系下 u(r,z,φ)满足:
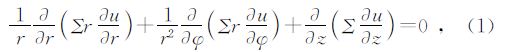
各电极表面为等电位面,满足相应的边界条件,各电极表面边界条件为

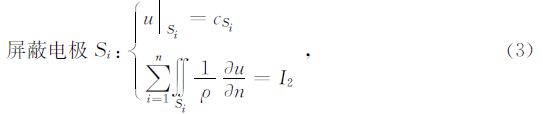
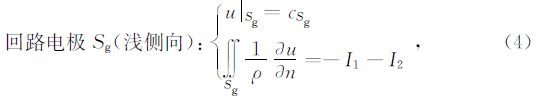

跟据研究区裂缝型低阻碳酸盐岩储层典型特征,设置基岩电阻率5 Ωm,椭球形裂缝延伸长度为3 m,仪器居于椭球形裂缝中心,模拟了裂缝开度为2 mm、5 mm、10 mm,不同视倾角裂缝的双侧向响应特征(图 3).
 | 图 3 视倾角对不同开度裂缝双侧向测井响应影响 Fig. 3 Effects of apparent angles towards dual-laterolog responses of different fracture widths |
由图 3可见,当裂缝开度一定,视倾角小于某一角度(临界角)时,深浅侧向电阻率之间出现负差异(Rlld<Rlls),并且随着角度的增大,负差异逐渐减小,当角度大于临界角时,深浅侧向视电阻率出现正差异(Rlld>Rlls),并且随着角度的增大,这种正差异逐渐变大,模拟趋势与前人研究结果一致(汪涵明和张庚骥,1994).
该变化主要是由深浅侧向响应区域不同所致(姜绍芹,2009).水平裂缝对聚焦较强的深侧向影响更为明显,从而使深侧向视电阻率值小于浅侧向,即为负差异;对于高角度缝(图 4,蓝色部分表示裂缝,d1为浅侧向探测深度,d2为深侧向探测深度),裂缝导电截面(蓝色部分)在径向上不变,而基岩的导电截面(以井眼为中心的圆环)在径向上是逐渐增大的,因此浅侧向裂缝与基岩的导电截面之比大于深侧向,从而使浅侧向视电阻率值小于深侧向,即为正差异.
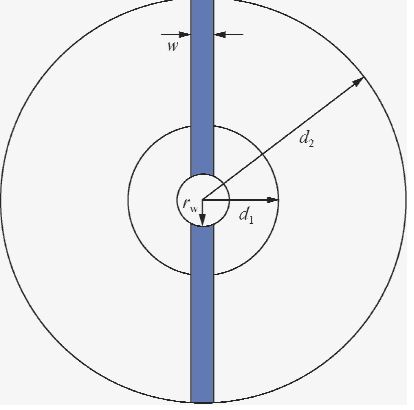 | 图 4 垂直裂缝模型 Fig. 4 Model of vertical fracture |
与以往高阻基岩中的双侧向测井响应不同,受低阻基岩导电影响,低阻碳酸盐岩储层临界角小于高阻基岩储层临界角(史謌等,2004),且临界角与裂缝开度呈正相关关系(图 3中2 mm,5 mm,10 mm裂缝临界角依次增大).
2.2 充填物电阻率的影响裂缝充填物电阻率对低阻储层测井响应影响复杂(李舟波,2004;田飞等,2012),本文根据三维有限元法模拟了裂缝充填物电阻率对双侧向测井响应的影响,模型中井眼为8.5 inch,基岩电阻率为2 Ωm,裂缝开度为1 mm,2 mm,10 mm.模拟结果如下:当充填物电阻率低于基岩时,深侧向视电阻率小于浅侧向,双侧向出现负幅度差,深浅侧向视电阻率之比小于1,深浅侧向视电阻率之比及幅度差随充填物电阻率减小而减小,当充填物电阻率减小到临界值后,深浅侧向视电阻率之比趋于稳定,幅度差反而增大,该临界值与裂缝开度,基岩电阻率等因素有关.当充填物电阻率高于基岩电阻率时,深浅侧向视电阻率之比大于1,双侧向出现正幅度差,深浅侧向视电阻率之比与充填物电阻率关系见图 5.
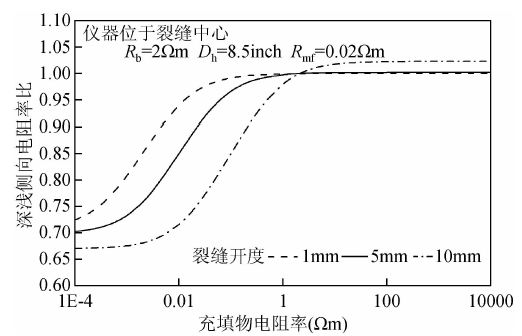 | 图 5 裂缝充填物电阻率对双侧向幅度差的影响 Fig. 5 Effects of filling substance resistivity towards dual-laterolog amplitude difference |
 | 图 6 基岩电阻率对双侧向影响 Fig. 6 Effects of surrounding rock resistivity towards dual-laterolog responses |
为了研究基岩电阻率对双侧向测井响应的影响,本文通过三维有限元法系统模拟了8.5 inch井眼中,基岩电阻率变化对开度为1 mm,2 mm,5 mm裂缝深浅侧向视电阻率影响,结果如下:深浅侧向测井响应与基岩电阻率成正相关关系;基岩电阻率变化对开度较小的裂缝影响较为明显;由于深浅侧向探测范围不同(图 4),深侧向受基岩电阻率变化影响较大.
由上述模拟可见,由于裂缝型低阻碳酸盐岩储层中基质孔隙发育,基岩导电明显,双侧向测井响应不同于高阻碳酸盐岩储层,目前常用的基于高阻碳酸盐岩的双侧向裂缝参数解释模型不适用于低阻基岩条件下.双侧向幅度差与裂缝角度,开度,流体、基岩电阻率以及仪器装置系数K等诸多因素有关,且幅度差相对于高阻基岩储层小.由此可见传统的适用于高阻储层的双侧向裂缝参数评价模型在低阻碳酸盐岩储层中适用性有限,亟需建立适用于裂缝型低阻碳酸盐岩的裂缝参数评价模型.
3 裂缝参数计算方法及刻度通过模拟认为双侧向对低阻流体填充的裂缝响应敏感,裂缝存在时将引起双侧向响应大幅变化.基岩双侧向视电阻率与裂缝中点处双侧向视电阻率之比随裂缝开度增大单调增大.因此采取利用裂缝中点处深(浅)侧向视电阻率与基岩深(浅)侧向视电阻率的比值,并在同时考虑裂缝内流体影响,裂缝倾角影响情况下,基于三维有限元模拟结果,制作了适合于低电阻率基岩的一系列裂缝开度计算图版(图 7).
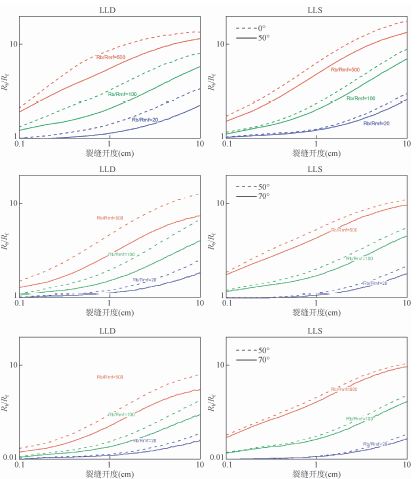 | 图 7 不同泥浆、基岩电阻率下的裂缝开度计算图版 Fig. 7 Fracture widths calculation chart of different mud resistivity and surrounding rock resistivity |
通过对上述图版中曲线进行分段拟合,然后对不同基岩电阻率与泥浆电阻率之比进行插值,确定了任意泥浆、基岩电阻率条件下的裂缝开度求解方程.由于拟合后方程复杂,鉴于篇幅关系仅写出简式:

实际应用中,双侧向测井反映的是一定深度范围内所有裂缝的响应叠加(汪涵明等,1995),需要采用电成像测井中反应一定深度范围内裂缝开度叠加的参数对双侧向计算开度进行刻度(蒲静和秦启荣,2008; 赵辉等,2012).研究中通过与叙利亚某油田的电成像评价结果进行对比,得出以下刻度关系:
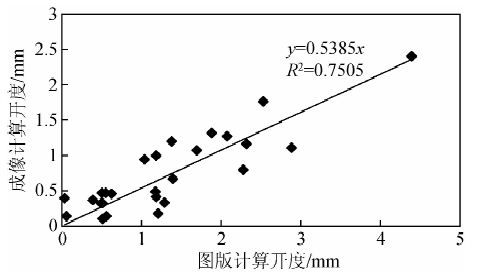 | 图 8 成像计算开度与图版计算开度交会图 Fig. 8 Cross plot of fracture width calculated by dual-laterolog and imaging log |
校正后开度为
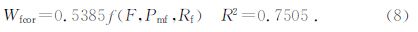
在确定了裂缝张开度后,可以采用成像测井裂缝面积孔隙度公式计算裂缝孔隙度.
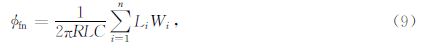
将该裂缝开度计算方法应用于实际裂缝型低电阻率碳酸盐岩储层资料处理中(以叙利亚低电阻率生物灰岩为例),利用双侧向求裂缝参数.
以研究区X1井为例(图 9),第五道为裂缝开度道,红线表示双侧向计算的裂缝开度,黑线表示成像测井计算开度.第六道为裂缝孔隙度道,红线表示双侧向计算的裂缝孔隙度,黑线表示成像测井裂缝孔隙度.可见该井从1330~1362 m共有3个裂缝发育段.1135.5 m处FMI解释裂缝开度为3.01 mm,双侧向模型解释为2.93 mm;1150.7 m处FMI解释裂缝开度为0.93 mm,双侧向模型解释裂缝开度为1.06 mm.1158.5 m处FMI响应为复杂剪破裂层段,剪张裂缝发育,常规测井电阻率明显下掉,密度减小,声波明显增大,井径扩径.Geoframe程序解释FMI资料裂缝开度达到3.7 cm,双侧向模型解释裂缝开度为3.2 cm,裂缝孔隙度峰值达到3.8%,裂缝极其发育,投产初期该层日产油978.3 bbl/d,气123.2 Mcf/d,水244 bbl/d.
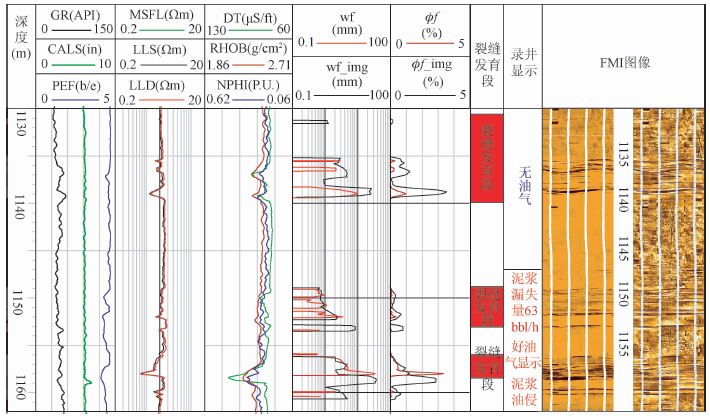 | 图 9 X1井综合解释图 Fig. 9 Comprehensive processing result in well X1 |
总体上双侧向对储层中裂缝响应明显,双侧向计算裂缝参数与成像计算参数基本一致.
5 结 论本文通过三维有限元法,分析了存在基质孔隙导电影响时,裂缝型低阻碳酸盐岩储层双侧向视电阻率与裂缝开度,角度,流体、基岩电阻率等裂缝参数间的定量关系.总结了裂缝型低阻碳酸盐岩储层双侧向响应特征,建立了利用双侧向视电阻率变化率求取裂缝参数方法,用成像测井对其刻度,并将该方法应用于裂缝型低阻碳酸盐岩储层中.模型论证和实例检验结论如下:
1)裂缝开度,角度,流体、基岩电阻率对低阻碳酸盐岩储层双侧向幅度差与临界点综合影响明显,传统的双侧向裂缝参数评价模型在低阻碳酸盐岩中应用效果较差.
2)基岩双侧向视电阻率与裂缝中点处双侧向视电阻率之比对裂缝响应敏感,随裂缝开度增大单调增大,综合考虑裂缝角度与裂缝内流体电阻率可用于地下较小开度的微裂缝定量评价.
应用证实该思路方法适用于裂缝型低阻基岩储层以及常规裂缝型高阻基岩储层.
致 谢 感谢审稿专家的热情支持.| [1] | Boyeldieu C, Winchester A. 1982. Use of the Dual Laterolog for the evaluation of the fracture porosity in hard carbonate formations[C]. //Offshore South East Asia Conference. Singapore: Society of Petroleum Engineers. |
| [2] | Deng S G, Wang X C, Fan Y R. 2006. Response of dual laterolog to fractures in fractured carbonate formation and its interpretation [J]. Earth Science (in Chinese), 31(6): 846-850. |
| [3] | Gao X, Xie Q B. 2007. Advances in identification and evaluation of fracture [J]. Progress in Geophysics (in Chinese), 22(5): 1460-1465. |
| [4] | Huang L L, Gao C F, Zhang C M, et al. 2002. Determining Equivalent Fracture Width with Dual Laterolog-On an Error in Sibbit Formula [J]. Journal of Jianghan Petroleum Institute (in Chinese), 24(4): 42-44. |
| [5] | Jiang S Q. 2009. Fracture parameter by DLL interpretation and its application to carbonate rock[J]. Natural Gas Technology (in Chinese), 3(6): 40-43. |
| [6] | Jing J E, Mei Z W, Li Z B. 2003. Investigation of well logging evaluation and identification methods for carbonate reservoirs with fracture and vug in Tahe oil field[J]. Progress in Geophysics (in Chinese), 18(2): 336-341. |
| [7] | Li J, Zhang C M, Xiao C W, et al. 2008. Quantitative evaluation method of fracturing sandstone reservoir and its application in Kuqa area, the Tarim basin[J]. Natural Gas Industry (in Chinese), 28(10): 25-27. |
| [8] | Li S J, Xiao C W, Wang H M, et al. 1996. Mathematical model of dual laterolog response to fracture and quantitative interpretation of fracture porosity[J]. Chinese J. Geophys. (in Chinese), 39(6): 843-852. |
| [9] | Li S J, Wang H M, Xiao C W, et al. 1997. Quantitative interpretation of fracture porosity in carbonates [J]. Well Logging Technology (in Chinese), 21(3): 205-214. |
| [10] | Li Z B. 2004. Problem and advance on the fluid typing for complex reservoirs using well log [J]. Oil & Gas Geology (in Chinese), 25(4): 356-362. |
| [11] | Liu C Y, Wei X C, Xu S F, et al. 2007. The overview of geophysical techniques in prediction of carbonate rock reservoir [J]. Progress in Geophysics (in Chinese), 22(6): 1815-1822. |
| [12] | Luo Z Y. 1990. Preliminary study on the calculation of fracture aperture using laterolog log [J]. Well Logging Technology (in Chinese), 14(2): 83-92. |
| [13] | Philippe A P, Roger N A. In situ measurements of electrical resistivity, formation anisotropy, and tectonic context [C]. SPWLA 31st Annual Logging Symposium. Lafayette, Louisiana, 24-27. |
| [14] | Pu J, Qin Q R. 2008. An overview of fracture prediction methods for oil and gas reservoirs[J]. Special Oil & Gas Reservoirs (in Chinese), 15(3): 9-13. |
| [15] | Shi G, He T, Wu Y Q, et al. 2004. A study on the dual laterolog response to fractures using the forward Numerical modeling[J]. Chinese. J. Geophys. (in Chinese), 47(2): 359- 363 |
| [16] | Sibbit A M, Faivre Q. 1985. The dual Laterolog Response in Fractured Rocks [C]. // SPWLA. 26th Annual Logging Symposium, Dallas, Texas,17-20. |
| [17] | Tian F, Jin Q, Li Y, et al. 2012. Identification of small fracture-vugs and their fillings through log interpretation in fractured-vuggy Ordovician reservoirs in Tahe oilfield[J]. Oil & Gas Geology (in Chinese), 33(6): 900-908. |
| [18] | Van Golf-Racht T D. 1982. Fundamentals of Fractured Reservoir Engineering [M]. New York: Elsevier Scientific Publishing Company. |
| [19] | Wang H M, Zhang G J. 1994. The dual laterolog response in dipping beds [J]. Well Logging Technology (in Chinese), 18(6): 408-412. |
| [20] | Wang H M, Zhang G J, Li S J, et al. 1995. The duallaterolog response of the single dipping fracture [J]. Journal of the University of Petroleum (in Chinese), 19(6): 12-24. |
| [21] | Wang X C, Fan Y R, Zhang G J. 2008. The calculation of fractured porosity based on dual laterolog data and its calibration [J]. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 30(5): 377-380. |
| [22] | Zhang F M, Chen Y G, Shao C R, et al. 2010. Comparison and improvement of facture opening estimation model based on dual-laterolog [J]. Well Logging Technology (in Chinese), 34(4): 339-342. |
| [23] | Zhao J L, Gong Z W, Li G, et al. 2012. A review and perspective of identifying and evaluating the logging technology of fractured carbonate reservoir [J]. Progress in Geophysics (in Chinese), 27(2): 537-547. |
| [24] | Zhao H, Shi X, Sima L Q. 2012. Study on porosity exponent, saturation and fracture porosity for fractured reservoirs[J], Progress in Geophysics (in Chinese), 27(6): 2639-2645. |
| [25] | Zhao Y W, Nie Z P. 1998. An algorithm for the inversion of resistivity measurements from dual laterolog tool [J]. Chinese J. Geophys. (in Chinese), 41(3): 424-431. |
| [26] | 邓少贵, 王晓畅, 范宜仁. 2006. 裂缝性碳酸盐岩裂缝的双侧向测井响应特征及解释方法[J]. 地球科学, 31(6): 846-850. |
| [27] | 高霞, 谢庆宾. 2007. 储层裂缝识别与评价方法新进展[J]. 地球物理学进展, 22(5): 1460-1465. |
| [28] | 黄烈林, 高纯福, 张超谟,等. 2002. 双侧向测井确定裂缝等效宽度——兼论Sibbit公式中的一个错误[J]. 江汉石油学院学报, 24(4): 42-44. |
| [29] | 姜绍芹. 2009. 双侧向测井裂缝参数解释方法的应用[J]. 天然气技术, 3(6): 40-43. |
| [30] | 景建恩, 梅忠武, 李舟波. 2003. 塔河油田碳酸盐岩缝洞型储层的测井识别与评价方法研究[J]. 地球物理学进展, 18(2): 336-341. |
| [31] | 李军, 张超谟, 肖承文,等. 2008. 库车地区砂岩裂缝测井定量评价方法及应用[J]. 天然气工业, 28(10): 25-27. |
| [32] | 李善军, 肖承文, 汪涵明,等. 1996. 裂缝的双侧向测井响应的数学模型及裂缝孔隙度的定量解释[J]. 地球物理学报, 39(6): 845- 852. |
| [33] | 李善军, 汪涵明, 肖承文,等. 1997. 碳酸盐岩地层中裂缝孔隙度的定量解释[J]. 测井技术, 21(3): 205- 214. |
| [34] | 李舟波. 2004, 利用测井方法识别复杂油气储层的流体性质[J]. 石油与天然气地质, 25(4): 356-362. |
| [35] | 刘春园, 魏修成, 徐胜峰,等. 2007. 地球物理方法在碳酸盐岩储层预测中的应用综述[J]. 地球物理学进展, 22(6): 1815-1822. |
| [36] | 罗贞耀. 1990. 用侧向资料计算裂缝张开度的初步研究[J]. 地球物理测井, 14(2): 83-92. |
| [37] | 蒲静, 秦启荣. 2008. 油气储层裂缝预测方法综述[J].特种油气藏, 15(3): 9-13. |
| [38] | 史謌, 何涛, 仵岳奇,等. 2004. 用正演数值计算方法开展双侧向测井对裂缝的响应研究[J]. 地球物理学报, 47(2): 359-263. |
| [39] | 田飞, 金强, 李阳,等. 2012. 塔河油田奥陶系缝洞型储层小型缝洞及其充填物测井识别[J]. 石油天然气地质, 33(6): 900-908. |
| [40] | 汪涵明, 张庚骥. 1994. 倾斜地层的双侧向测井响应[J]. 测井技术, 18(6): 408-412. |
| [41] | 汪涵明, 张庚骥, 李善军,等. 1995. 单一倾斜裂缝的双侧向测井响应[J]. 石油大学学报, 19(6): 12-24. |
| [42] | 王晓畅, 范宜仁, 张庚骥. 2008. 基于双侧向测井资料的裂缝孔隙度计算及其标定[J]. 物探化探计算技术, 30(5): 377-380. |
| [43] | 张福明, 陈义国, 邵才瑞,等. 2010. 基于双侧向测井的裂缝开度估算模型比较及改进[J]. 测井技术, 34(4): 339-342. |
| [44] | 赵军龙, 巩泽文, 李甘,等. 2012. 碳酸盐岩裂缝性储层测井识别及评价技术综述与展望[J]. 地球物理学进展, 27(2): 537-547. |
| [45] | 赵辉, 石新, 司马立强. 2012. 裂缝性储层孔隙指数、饱和度及裂缝孔隙度计算研究[J]. 地球物理学进展, 27(6): 2639-2645. |
| [46] | 赵延文, 聂在平. 1998. 双侧向电阻率测井反演算法研究[J]. 地球物理学报, 41(3): 424-431. |
 2014, Vol. 29
2014, Vol. 29

