地球物理学进展  2014, Vol. 29 Issue (5): 2211-2218   PDF    
引用本文
刘诗竹, 石颖, 郭雪豹, 王维红. VSP数据逆时偏移方法研究[J]. 地球物理学进展, 2014, 29(5): 2211-2218, doi: 10.6038/pg20140533  
LIU Shi-zhu, SHI Ying, GUO Xue-bao, WANG Wei-hong. Investigation on reverse-time migration of VSP data. Progress in Geophysics, 2014, 29(5): 2211-2218, doi: 10.6038/pg20140533   
VSP数据逆时偏移方法研究
刘诗竹1, 石颖1,2 , 郭雪豹1, 王维红3    
1. 东北石油大学地球科学学院, 大庆 163318;
2. 黑龙江省普通高校科技创新团队“断层变形、封闭性及与流体运移”, 大庆 163318;
3. 大庆油田有限责任公司勘探开发研究院, 大庆 163712
收稿日期: 2013-11-23 修回日期: 2014-3-4 .
基金项目：中石油科技创新基金项目(2011D-5006-0304)和黑龙江省教育厅科学技术研究项目(12511025)联合资助.
作者简介：刘诗竹,女,1989年生,河北任丘人,东北石油大学在读硕士研究生,主要从事地震资料处理方面的研究. (E-mail: vicky04280@126.com)
通讯作者：石颖,女,博士,教授,博士生导师,现工作于东北石油大学地球科学学院,主要从事地震资料处理方面的研究. (E-mail: shiyingdqpi@163.com)
摘要：相比于地面地震,VSP数据地震勘探具有高分辨率和高信噪比的特点,目前常规的VSP数据偏移方法难于获得理想的成像效果,逆时偏移方法(RTM)基于双程波动方程,迄今为止被认为是精度最高的地震资料偏移算法.文中依据VSP数据采集特点,从二维声波波动方程入手,研究基于高阶有限差分数值算法的VSP数据逆时偏移,数值计算采用节约部分存储的完全匹配层吸收边界条件(PML),在有效抑制地震波场的边界反射以及保持波场精度的情况下,很大程度上节约了波场存储.文中也采用了互相关成像条件以及拉普拉斯低频噪声压制技术,实现了VSP数据逆时偏移的高精度成像.测试表明,高精度的逆时偏移方法可有效成像VSP地震数据,可实现对小断层构造、大角度构造,以及井周小构造的精细刻画.
关键词： VSP     逆时偏移     PML边界     波场存储     断层构造    
Investigation on reverse-time migration of VSP data
LIU Shi-zhu1, SHI Ying1,2 , GUO Xue-bao1, WANG Wei-hong3    
1. School of Earth Sciences, Northeast Petroleum University, Daqing 163318, China;
2. Science and Technology Innovation Team on Fault Deformation, Sealing and Fluid Migration, Daqing 163318, China;
3. Daqing Oil Field Exploration and Development Research Institute, Daqing 163712, China
Abstract: Compared with ground seismic exploration, VSP seismic exploration has the characteristics of high resolution and high signal to noise ratio. At present, conventional VSP data migration methods are difficult to obtain the ideal imaging effect. Based on the two-way wave equation, the reverse-time migration(RTM) has become the most accurate migration method so far. In this paper, on the basis of VSP data acquisition characteristics, we deal with VSP data by high order finite difference algorithm during the RTM based on 2D acoustic wave equation. We adopt the perfect matched layer absorbing boundary condition(PML) by the way of setting checkpoints, so that we saved the wave fields storage, in the meantime, effectively suppressed the boundary reflection of seismic wave fields and kept the precision. We also used the cross-correlation imaging condition and laplacian low frequency noise suppression technique to make the high resolution image with reverse-time migration of VSP data come true. The test indicated that high precision reverse-time migration could validly image VSP data and nicely depict small faults, large angle structure and the local area around the well.
Key words: VSP     reverse-time migration     PML boundary     wave fields storage     fault structure    
0 引 言

随着勘探程度的不断深入，勘探目标日趋复杂化，薄层、隐蔽油气层等复杂地质构造的识别对地震资料处理技术提出了更高的要求.由于VSP观测系统采用地面激发，井中接收，理论上VSP成像可获得高精度的成像剖面，自上世纪五十年代开始，国内外的众多专家一直致力于VSP数据的应用和成像研究.苏联科学界首先提出垂直地震剖面的概念，随后逐步形成了系统的VSP观测方法.Seeman(1983)等提出对分层介质模拟的VSP数据分离上下行波的方法，Chang和McMechan(1986)提出应用激发时刻成像条件的逆时偏移方法处理非零偏移距VSP数据，Dillon(1988)采用克希霍夫积分法对VSP数据进行偏移.八十年代后，朱光明(1988)将VSP技术引入国内，并推动了VSP技术的快速发展.近年来，VSP数据在成像小断层构造、大角度构造以及井周构造等方面的优势，再次获得国内众多学者的重视，王珺等(2006)利用克希霍夫法成像VSP数据；高静怀等(2007，2008)利用VSP资料提取介质品质因子；邹延延等(2009)从正反演的角度讨论了VSP的发展；余振等(2010)针对VSP资料提出一种稳定的反Q滤波方法；张山等(2011)提出将目的层以上地层均校正为横向均匀介质的自适应静校正法；刘守伟等(2012)通过修改波场延拓的方式，提出上下行反射波联合成像方法；朱海龙等(2012)提出高保真VSP波场分离方法，大大降低了混波作用.

逆时偏移方法不受成像角度限制、可以准确描述各种波，最早由Whitmore(1983)，Baysal(1983)，McMechan等(1983)提出.随后Chang等(1987)提出基于弹性波的逆时偏移方法.然而，由于计算成本高，存储量巨大，逆时偏移方法在实际生产中并未获得广泛的应用.近年来，随着计算机硬件技术的迅速发展，逆时偏移方法再次成为成像技术的焦点，并从算法技巧和并行技术两方面大幅度提高了计算效率.徐义(2008)提出非规则网格算法的格子法逆时偏移；董春晖、王尚旭(2010)提出了一种针对不同的时间段，采用不同时间步长计算该时间段所对应空间范围内波场的逆时偏移算法；郭念民、吴国忱(2012)给出了逆时偏移的变网格算法.李博(2010)和刘红伟等(2010a，2011)给出了利用GPU技术实现叠前逆时偏移的高阶有限差分算法，大幅提高了计算效率.

本文利用基于高阶有限差分的叠前逆时偏移方法成像VSP数据，改进的PML边界条件在消除地震波场边界反射的同时，可节约大部分存储空间，采用拉普拉斯滤波法有效压制VSP数据低频成像噪声.不同地质构造模型测试表明，VSP数据逆时偏移方法可实现复杂构造精细成像，相比于常规地面地震逆时偏移，含丰富波场信息的VSP数据逆时偏移对小断层、井周薄层、高陡倾角等复杂构造成像更具优势，可实现复杂地质体的精细刻画.

1 VSP技术原理

VSP的观测系统如图 1所示，震源布置在地表，检波器沉放在井中，是一种地表激发井中接收的观测方式.由于VSP检波器分布在地下，相比于地面地震，VSP记录的波场信息更为丰富，如图 2所示，地震波场不仅包含上行波(一次反射波、上行多次波)，还包括下行波(直达波、下行多次波)，其能够直接采集到来自目的层的信息，减少地下低速带对反射信号的影响，同时也更便于接收高陡倾角构造的反射信息.因此，VSP数据的信噪比和分辨率更高.

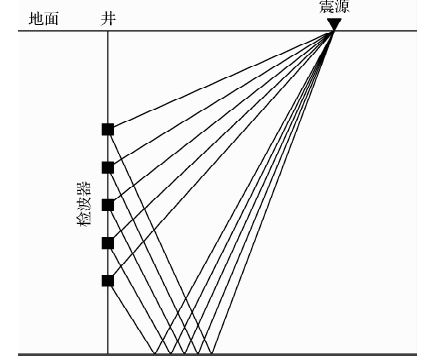图 1 VSP观测系统 Fig. 1 Seismic acquisition geometry of VSP

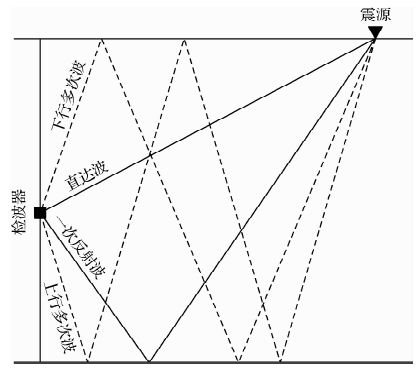图 2 VSP波场信息 Fig. 2 Seismic data of VSP
2 逆时偏移方法基本原理

叠前深度逆时偏移主要包括地震波场延拓计算、成像条件应用以及低频噪音压制三个过程.文中采用高阶有限差分数值算法求解波动方程，模拟地震波正向传播的过程，并保存每一时刻的地震波场信息.然后读取炮集记录放于检波点处进行波场反传，并将反传每一时刻波场与对应时刻的正传波场互相关成像，最后利用拉普拉斯低频噪声压制技术去除叠加成像数据的低频噪音.

2.1 高阶有限差分格式

对二维声波方程

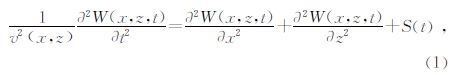
式中，W(x，z，t)为t时刻点(x，z)处的波场值；S(t)表示震源函数；v表示介质速度.

应用时间二阶、空间2L阶精度差分格式，得出二维声波方程的有限差分形式为

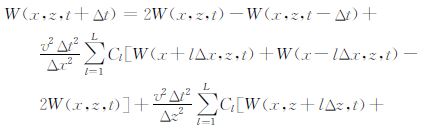
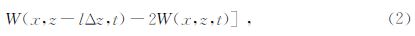
式中，Δt为时间步长，Δx、Δz分别为x方向和z方向的网格大小.本文采用时间2阶、空间16阶有限差分格式，差分系数Cl的值可依据下式求出(刘洋等，1998)：

(3)式可进一步表述为

2.2 边界条件

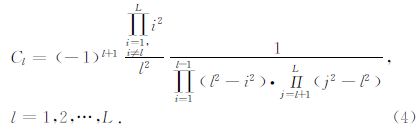
由于计算机存储有限，无法实现无限传播的地下波场模拟，因此有限区域的数值计算存在边界反射干扰，在数值求解过程中，需要有效的边界处理方法削弱边界反射对波场的影响.本文采用PML吸收边界条件，在数值计算波场的边界添加吸收层，使波传播到边界时被吸收层吸收衰减，该方法不受边界吸收角度的限制，可以吸收任意方向、任意频率的波，迄今为止，认为是精度最高的边界处理方法.

对应二维声波方程的完全匹配层控制方程为(王守东，2003)

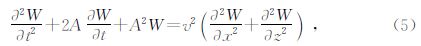
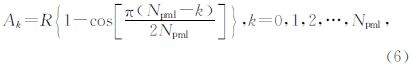
式中，A为吸收衰减因子，本文采用余弦型衰减因子(陈可洋，2010；高刚等，2011)

式中，Ak为吸收衰减因子，R为衰减幅度因子，Npml为吸收层的网格点数.k=0时，Ak表示模型吸收区的外边界吸收衰减因子，吸收衰减量最大；k=Npml时，Ak表示模型吸收区的内边界吸收衰减因子，吸收衰减量最小.吸收衰减因子Ak由沿x方向和z方向衰减的因子Ax和Az分量组成，吸收衰减因子的模型分布示意图如图 3 所示，按能量衰减的大小，模型边界可分为三部分：仅沿x方向吸收衰减的1号区，衰减因子Ax≠0，Az=0；仅沿z方向吸收衰减的2号区，衰减因子Ax=0，Az≠0；沿x和z方向均有吸收衰减的3号角区，衰减因子Ax≠0，Az≠0.

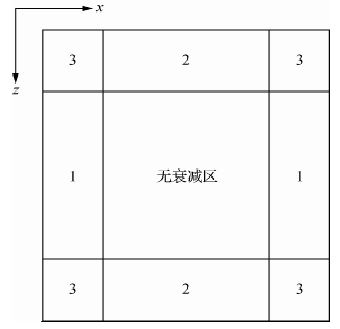图 3 吸收衰减因子模型分布示意图 Fig. 3 Sketch map for absorption attenuation factor distribution

尽管常规PML边界条件保证了地震波场数值模拟的精度，但相比于随机边界方法，应用PML边界需消耗大量的内存资源，鉴于此，本文采用设置检测点的方式，仅存储模型无衰减区域外层边界各时刻的波场(胡昊，2013)，在波场反传各时刻，重拾存储的正传波场信息，类似于随机边界以计算换存储的思想，却不同于随机边界，其不受随机噪音干扰，可获得更高精度的波场信息.

2.3 成像条件

互相关成像条件使用时间为唯一判断标准，可以处理多波至问题并快速稳定地成像，不会丢失波场信息，还能有效压制随机噪音.数学表达式(王娟等，2012)为

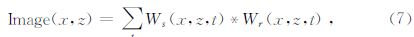
式中，Ws(x，z，t)为震源波场，Wr(x，z，t)为接收波场，同一时刻的震源波场和接收波场进行互相关运算，将每一时刻的成像值叠加，得到偏移结果.

另外，本文采用拉普拉斯低频噪声压制法对偏移结果进行去噪处理(刘洪伟，2010b).

3 模型试算

文中利用高阶有限差分数值算法正演断层构造模型、底辟构造模型以及Salt-2d模型的Walkaway VSP数据，利用前文述及的逆时偏移方法测试成像效果，有关正演计算此处不详述.

3.1 断层构造模型

设计如图 4a所示断层地质体，模型网格大小为1000×1000，纵横向空间步长均为5 m，在地表距左端25 m和4975 m处分别布设两口观测井，1号井和2号井，从地下5 m开始，每口井沉放1000级检波器，检波器间距为5 m.炮点位于地表，从左端100 m处开始，炮间距100 m，共49炮，震源采用主频40 Hz的雷克子波，时间步长为0.4 ms，时间采样点数为11250.1号井第3到5炮的VSP记录如图 4b所示，全部VSP记录的逆时偏移结果如图 4c所示，低频噪声干扰严重，拉普拉斯方法去噪处理后的结果如图 4d所示，断层刻画清晰，高陡倾角构造准确成像.

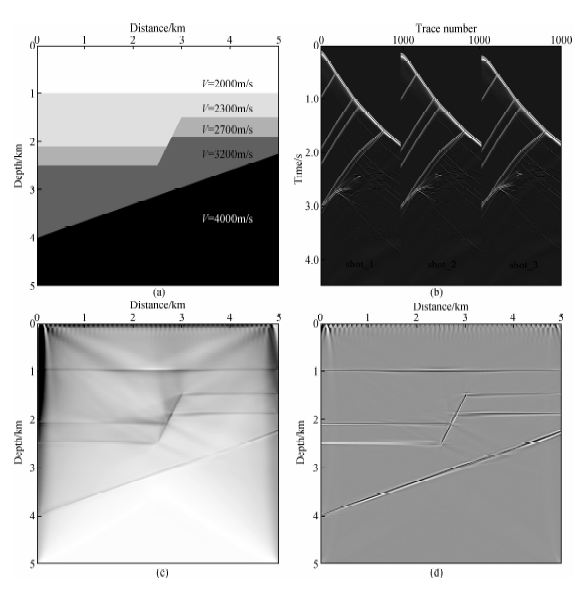图 4(a)断层速度模型；(b)1号井三炮VSP记录；(c)VSP逆时偏移剖面(去噪前)； (d)VSP逆时偏移剖面(去噪后). Fig. 4(a)Fault velocity model;(b)Three shots of VSP records from no.1 well; (c)RTM images of VSP data(before denoising);(d)RTM images of VSP data(after denoising).
3.2 底辟构造模型

设计如图 5a所示的底辟构造地质体，模型网格大小为3000×2500，纵横向空间步长均为5 m.采用VSP以及地面地震两种观测方法，比较两种偏移结果.VSP观测方法：在距左端25 m和2975 m处分别布设两口观测井，1号井和2号井，每口井沉放500级检波器，从地下5 m开始，检波器间距为5 m.炮点位于地表，从左端50 m处开始，炮间距100 m，共29炮.地面地震观测方法：检波器布置在地表，从模型左端到右端每隔5 m布置一个.炮点的位置与VSP观测方法的炮点位置一致，共29炮.两种方法均采用主频为40 Hz的雷克子波，时间步长为0.4 ms，采样点数为7500.1号井第4至6炮的VSP记录如图 5b所示，第4至6炮地面地震记录如图 5c所示.全部VSP记录的逆时偏移剖面如图 5d所示，有严重的低频噪音干扰，应用拉普拉斯方法去噪处理后如图 5f所示.全部地面地震记录的逆时偏移剖面如图 5e所示，应用拉普拉斯方法去噪处理后如图 5g所示.比较图 5f和图 5g的偏移结果，在图中圈出的小断层以及大角度构造等位置，VSP数据偏移结果更清晰，分辨率更高，体现出VSP资料对小断层以及大角度构造成像的优势.

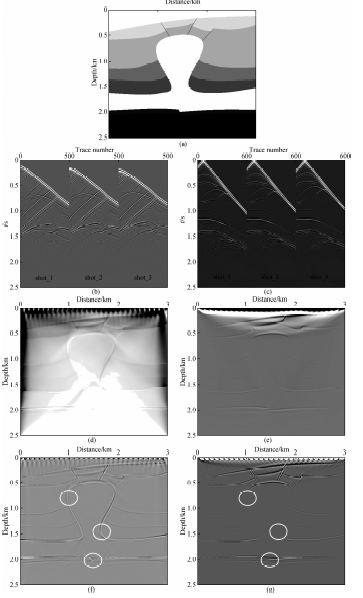图 5(a)底辟构造速度模型；(b)1号井三炮VSP记录；(c)三炮地面地震记录； (d)VSP逆时偏移剖面(去噪前)；(e)地面地震逆时偏移剖面(去噪前)； (f)VSP逆时偏移剖面(去噪后)；(g)地面地震逆时偏移剖面(去噪后). Fig. 5(a)diapiric structure velocity model;(b)Three shots of VSP records from no.1 well; (c)Three shots of the ground seismic records;(d)RTM images of VSP data(before denoising); (e)RTM images of ground seismic data(before denoising);(f)RTM images of VSP data(after denoising); (g)RTM images of ground seismic data(after denoising).
3.3 Salt-2d盐丘模型

Salt-2d盐丘模型如图 6a所示，网格大小为649×150，纵横向空间步长均为10 m.在距左端10 m，3250m和6480 m 处分别布设了三口观测井，1号井至3号井，每口井沉放150级检波器，从地下10 m开始，检波器间距为10 m.炮点位于地表，从左端100 m开始，炮间距100 m，共64炮.震源采用主频为40 Hz的雷克子波，时间步长为0.3 ms，时间采样点数为15000.3号井第61至63炮VSP记录如图 6b.对1号和3号两口井的VSP记录进行逆时偏移获得的剖面如图 6c所示，应用拉普拉斯方法去噪处理后如图 6e所示.对1号至3号三口井的VSP记录进行逆时偏移获得的剖面如图 6d所示，应用拉普拉斯方法去噪处理后如图 6f所示.比较图 6e与图 6f的偏移结果，可以看到图 6f中，2号井周的成像效果明显优于图 6e中的同一位置，尤其是两图中圈出的位置，图 6f中刻画出了两个小断层，而图 6e中则没有，体现出VSP资料对井周地层构造的精细成像.

图 6(a)Salt-2d速度模型；(b)3号井三炮VSP记录； (c)两口井的VSP逆时偏移剖面(去噪前)；(d)三口井的VSP逆时偏移剖面(去噪前)； (e)两口井的VSP逆时偏移剖面(去噪后)；(f)三口井的VSP逆时偏移剖面(去噪后). Fig. 6(a)Salt-2d velocity model;(b)Three shots of VSP records from no.3 well; (c)RTM images of VSP data from two wells(before denoising); (d)RTM images of VSP data from three wells(before denoising); (e)RTM images of VSP data from two wells(after denoising); (f)RTM images of VSP data from three wells(after denoising).
4 结 论

由于VSP的特殊观测方式，使得VSP数据较地面地震资料信噪比、分辨率更高.传统成像方法难于发挥VSP资料的优势，成像效果不甚理想.本文充分结合基于双程波方程逆时偏移方法的高精度成像优势和VSP数据优势，实现了复杂构造VSP数据的精确成像.兼顾计算精度和效率，文中采用高阶有限差分数值算法求解波动方程，设定检测点的改进PML边界条件方法，在确保高精度成像的同时，在很大程度上缓解了存储压力，拉普拉斯去噪方法压制低频噪音成效显著.不同地质体模型测试表明，VSP数据逆时偏移对小断层、高陡倾角等复杂构造成像优势明显，井周细节刻画清晰，VSP逆时偏移研究将有力地推动油藏地球物理的发展.

致 谢 本文部分研究内容受到大庆油田有限责任公司项目“3D VSP地震逆时偏移关键技术研究”资助，在此表示感谢.
参考文献
[1] Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration[J]. Geophysics, 48(11): 1514-1524.
[2] Chang W F, McMechan G A. 1986. Reverse time migration of offset vertical seismic profiling data using the excitation time imaging condition[J]. Geophysics, 51(1): 67-84.
[3] Chang W F, McMechan G A. 1987. Elastic reverse-time migration[J]. Geophysics, 52(10): 1365-1375.
[4] Chen K Y. 2010. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 49(5): 472-477.
[5] Dillon P B. 1988. Vertical seismic profile migration using the Kirchhoff integral[J]. Geophysics, 53(6): 786-799.
[6] Dong C H, Wang S X. 2010. Finite-difference method with variable time-steps for reverse-time migration[J]. Progress in Geophys, 25(4): 1298-1305, doi:10.3969/j.issn.1004-2903.2010.04.018.
[7] Gal'perin E I. 1974. Vertical seismic profiling[M]. Society of Exploration Geophysicists special Publication.
[8] Gao G, He Z H, Huang D J, et al. 2011. The attenuation factor analysis perfect matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 50(5): 430-433.
[9] Gao J H, Yang S L. 2007. On the method of quality factors estimation from zero offset VSP data[J]. Chinese J.Geophys. (in Chinese), 50(4): 1198-1209.
[10] Gao J H, Yang S L, Wang D X. 2008. Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data[J]. Chinese J.Geophys. (in Chinese), 51(3): 853-861.
[11] Guo N M, Wu G C. 2012. High-order finite difference acoustic equation based on PML boundary with variable grids for reverse-time migration[J]. Oil geophysics prospecting, 47(2): 256-265.
[12] Hu H, Liu Y K, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration. Chinese J, Geophys. (in Chinese), 56(6): 2033-2042, doi:10.6038/cjg20130624.
[13] Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese J. Geophys. (in Chinese), 53(12): 2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017.
[14] Liu H W, Li B, Liu H, et al. 2010a. The algorithm of high order finite different pre-stack reverse time migration and GPU implementation[J]. Chinese J. Geophys. (in Chinese), 53(7): 1725-1733, doi:10.3969/j.issn.0001-5733.2010.07.024.
[15] Liu H W, Liu H, Zou Z, et al. 2010b. The problems of denoise and storage in seismic reverse time migration[J]. Chinese J. Geophys. (in Chinese), 53(9): 2171-2180, doi:10.3969/j.issn.0001-5733.2010.09.017.
[16] Liu H W, Liu H, Li B, et al. 2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology[J]. Chinese J. Geophys. (in Chinese), 54(7): 1883-1892, doi:10.3969/j.issn.0001-5733.2011.07.022.
[17] Liu S W, Wang H Z, Chen S C, et al. 2012. Joint imaging method of VSP upgoing and downgoing reflection wave[J]. Chinese J.Geophys. (in Chinese), 3126-3133, doi:10.6038/j.issn.0001-5733.2012.09.030.
[18] Liu Y, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy[J]. Oil geophysical prospecting, 33(1): 1-10.
[19] McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 31: 413-420.
[20] Seeman B, Horowicz L. 1983. Vertical seismic profiling: separation of upgoing and downgoing acoustic waves in a stratified medium[J]. Geophsics, 48(5): 555-568.
[21] Wang J, Li Z C, Tao L. 2012. The research on imaging condition of reverse time migration[J]. Progress in Geophysics, 27(3): 1173-1182.
[22] Wang J, Yang C C, Liu H H, et al. 2006. VSP multiwave image with Kirchhoff Method[J]. Progress in Geophysics, 21(3): 845-855, doi:10.6038/j.issn.1004-2903.2012.03.042.
[23] Wang S D. 2003. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting, 38(1): 31-34.
[24] Whitmore N D. 1983. Iterative depth migration by backward time propagation[A]. 53rd SEG Meeting, Expanded Abstracts[C], 382-385.
[25] Xu Y. 2008. Prestack reverse-time migration by the grid method[J]. Progress in Geophysics, 23(3): 839-845.
[26] Yu Z, Wang Y C, He J. 2010. A stable inverse Q filtering method for VSP[J]. Progress in Geophysics, 25(5): 1676-1684, doi:10.3969/j.issn.1004-2903.2010.05.021.
[27] Zhang S, Zhu H L, Wang J Y, et al. 2011. Walk-away VSP and 3D-VSP self-adapted static correction method[J]. Progress in Geophysics, 26(5): 1755-1762, doi:10.3969/j.issn.1004-2903.2011.05.030.
[28] Zhu H L, Zhang S. 2012. A high fidelity VSP method of wavefield separation[J]. Progress in Geophysics, (4): 1557-1564, doi:10.6038/j.issn.1004-2903.2012.04.032.
[29] Zhu G M. 1988. Vertical seismic profiling method[M]. Beijing: Petroleum industry press.
[30] Zou Y Y, Xu Y X, Sha C. 2009. Review on the forward modeling and inversion of vertical seismic profile[J]. Progress in Geophysics, 24(1): 145-153.
[31] 陈可洋. 2010. 完全匹配层吸收边界条件研究[J]. 石油物探, 49(5): 472-477.
[32] 董春晖, 王尚旭. 2010. 变时间步长有限差分法逆时偏移[J]. 地球物理学进展, 25(4): 1298-1305, doi:10.3969/j.issn.1004-2903.2010.04.018.
[33] 高刚, 贺振华, 黄德济, 等. 2011. 完全匹配层人工边界条件中的衰减因子分析[J]. 石油物探, 50(5): 430-433.
[34] 高静怀, 杨森林. 2007. 利用零偏移VSP资料估计介质品质因子方法研究[J]. 地球物理学报, 50(4): 1198-1209.
[35] 高静怀, 杨森林, 王大兴. 2008. 利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子[J]. 地球物理学报, 51(3): 853-861.
[36] 郭念民, 吴国忱. 2012. 基于PML边界的变网格高阶有限差分声波方程逆时偏移[J]. 石油地球物理勘探, 47(2): 256-265.
[37] 胡昊, 刘伊克, 常旭, 等. 2013. 逆时偏移计算中的边界处理分析及应用[J]. 地球物理学报, 56(6): 2033-2042, doi:10.6038/cjg20130624.
[38] 李博, 刘红伟, 刘国峰, 等. 2010. 地震叠前逆时偏移算法的CPU/GPU实施对策[J]. 地球物理学报, 53(12): 2938-2943, doi:10.3969/j.issn.0001-5733.2010.12.017.
[39] 刘红伟, 李博, 刘洪, 等. 2010a. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 53(7): 1725-1733, doi:10.3969/j.issn.0001-5733.2010.07.024.
[40] 刘红伟, 刘洪, 邹振, 等. 2010b. 地震叠前逆时偏移中的去噪与存储[J]. 地球物理学报, 53(9): 2171-2180, doi:10.3969/j.issn.0001-5733.2010.09.017.
[41] 刘红伟, 刘洪, 李博, 等. 2011. 起伏地表叠前逆时偏移理论及GPU加速技术[J]. 地球物理学报, 54(7): 1883-1892, doi:10.3969/j.issn.0001-5733.2011.07.022.
[42] 刘守伟, 王华忠, 陈生昌, 等. 2012. VSP上下行反射波联合成像方法研究[J]. 地球物理学报, 3126-3133, doi:10.6038/j.issn.0001-5733.2012.09.030.
[43] 刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分数值模拟[J]. 石油地球物理勘探, 33(1): 1-10.
[44] 王娟, 李振春, 陶丽. 2012. 逆时偏移成像条件研究[J]. 地球物理学进展, 27(3): 1173-1182, doi:10.6038/j.issn.1004-2903.2012.03.042.
[45] 王珺, 杨长春, 刘海河, 等. 2006. 克希霍夫法VSP多波联合成像[J]. 地球物理学进展, 21(3): 845-855.
[46] 王守东. 2003. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 38(1): 31-34.
[47] 徐义. 2008. 格子法在起伏地表叠前逆时偏移深度偏移中的应用[J]. 地球物理学进展, 23(3): 839-845.
[48] 余振, 王彦春, 何静. 2010. 一种稳定的VSP反Q滤波方法[J]. 地球物理学进展, 25(5): 1676-1684, doi:10.3969/j.issn.1004-2903.2010.05.021.
[49] 朱海龙, 张山. 2012. 高保真VSP波场分离方法研究[J]. 地球物理学进展, (4): 1557-1564, doi:10.6038/j.issn.1004-2903.2012.04.032.
[50] 张山, 朱海龙, 王家映, 等. 2011. Walk-away VSP和3D-VSP自适应静校正方法研究[J]. 地球物理学进展, 26(5): 1755-1762, doi:10.3969/j.issn.1004-2903.2011.05.030.
[51] 邹延延, 徐义贤, 沙椿. 2009. VSP正反演综述[J]. 地球物理学进展, 24(1): 145-153.
[52] 朱光明. 1988. 垂直地震剖面方法[M]. 北京: 石油工业出版社.