地球物理学进展  2014, Vol. 29 Issue (5): 2100-2105   PDF    
引用本文
尹正, 杨雪霖, 李振春. 频率域波动方程菲涅尔带走时层析成像方法[J]. 地球物理学进展, 2014, 29(5): 2100-2105, doi: 10.6038/pg20140516  
YIN Zheng, YANG Xue-lin, LI Zhen-chun. Fresnel zone traveltime tomography based on frequency-domain wave equation. Progress in Geophysics, 2014, 29(5): 2100-2105, doi: 10.6038/pg20140516   
频率域波动方程菲涅尔带走时层析成像方法
尹正, 杨雪霖, 李振春    
中国石油大学(华东)地球科学与技术学院, 青岛 266580
收稿日期: 2013-11-19 修回日期: 2014-5-9 .
基金项目：国家自然基金(41204086)、国家863课题(2011AA060301)和国家科技重大专项(2011ZX05006-002)共同资助.
作者简介：尹正,男,1989年生,硕士,主要从事地震波速度建模与层析反演成像方法研究.(E-mail:yzalex331@gmail.com)
摘要：传统的走时层析反演都是依赖于射线理论,而实际地震资料的带限特征与射线理论无限高频的假设存在理论上的矛盾.针对传统的射线层析存在的上述问题,本文从频率域波动方程的Born和Rytov近似入手,推导出菲涅尔带走时层析敏感核函数,其与传统的射线层析方法的显著区别在于它建立在带限地震波与第一菲涅尔带的理论基础上.通过射线走时残差与Rytov近似走时残差的比较,本文提出了依据Rytov近似走时残差的菲涅尔层析反演方法.表层速度模型试算结果表明,相对于传统的射线走时层析,基于频率域波动方程的菲涅尔带走时层析成像方法具有更高的成像精度与分辨率.
关键词： 走时层析     菲涅耳带     核函数     Born近似     Rytov近似    
Fresnel zone traveltime tomography based on frequency-domain wave equation
YIN Zheng, YANG Xue-lin, LI Zhen-chun    
School of Geoscience, China University of Petroleum (East China), Qingdao 266580 China
Abstract: In the traditional seismic imaging experiments, ray theory plays an important role in gaining the velocity construction. In reality, recorded wave signal is band-limited which is contradictive with the infinite-frequency assumption. We start from the Born and Rytov approximation of frequency-domain wave equation to derive the traveltime sensitivity kernels for Fresnel zone tomography. It is distinguished from the ray theory in that the sensitivity is established on the band-limited wave signal and the first Fresnel zone. We present Fresnel zone tomography based on the Rytov approximation traveltime delay by comparing it with ray theory traveltime delay. We apply our method into the construction of the near surface velocity model. The inverted result proves that our method has a higher resolution and accuracy when comparing with the ray theory tomography.
Key words: traveltime tomography     Fresnel zone     sensitivity kernels     Born approximation     Rytov approximation    
0 引 言

地震速度建模方法主要有三类：常规叠加速度分析(Garotta，1967)，基于道集分析类的偏移速度建模方法(Faye，1986; Al-Yahya，1989)，反演类的速度建模方法(Jin，2000)，三类方法经历了交叉发展的过程，精度依次提高.层析成像作为目前理论上精度相对较高的速度建模方法最早是应用在医学领域，于20世纪70年代由Bois(1972)等引入到地球物理勘探领域，由此开启了层析反演的研究热潮.

层析反演方法主要包括：射线层析和波动层析两大类.在传统的地震层析成像中，射线理论一直扮演着重要的角色.射线理论流行的重要原因主要在于以下两个方面：(1)计算机计算和存储能力的不足；(2)射线理论在地震成像方法中容易实现.但是，射线理论是波动方程的一种高频近似.射线理论的适用要满足两个假设条件：首先，速度扰动体在相当于地震波波长尺度上的变化要非常平滑，在这种情况下，是不存在散射的，也就是说相位的扰动是与频率呈线性关系并且地震子波不会发生畸变；另一方面，因为不存在散射，射线是一条无限细的线，只会覆盖速度场非常小的部分，且射线对经过的速度扰动体产生的走时扰动具有记忆能力，并不会在后续的传播中减小.因此无法根据单一的观测到的旅行时扰动来确定速度扰动的位置，而需大量的旅行时扰动信息.因此射线层析要求观测系统必须提供足够的观测视角，这就要求大量的炮检点，而在实际中，并不能满足这个要求，因此射线层析求解存在很大的不适定性.上述问题严重制约了射线层析反演的发展.

为了解决层析反演存在的上述问题，上世纪90年代出现了波动方程层析成像方法(Luo，1990).波动方程层析不存在射线的高频假设，因此理论上应该有更高的反演精度.但是相对于射线层析而言，波动方程层析中速度扰动与目标函数之间往往呈现非常强的非线性关系，导致反演容易陷入局部极值而无法收敛，这就需要精度很高的初始速度模型，给初始速度建模以及迭代反演带来的很大的困难.

为了寻求一种介于射线和波动方程层析之间并兼顾两者优点的层析方法，地球物理学家们开展了大量深入细致的研究，张建中(2007)，(2009)等人提出了基于第一菲涅尔带定义下的胖射线层析方法，该方法虽然在一定程度上降低了射线层析矩阵的稀疏性，但其仍然束缚在射线理论的框架内，无法回避射线层析存在的理论假设，Dahlen(2000)与zhao(2007)等人建立有限频层析成像理论，该理论针对带限地震波的事实，考虑地震波在非均匀介质中的绕射引起的波前弥合效应，在Born与Rytov近似的理论基础上，建立了旅行时残差与介质速度扰动之间的线性关系.这种线性关系较为精确的刻画了空间位置点对波前走时的影响，这种影响用核函数来表示，即Frechet核函数.有限频层析既有射线理论线性反演的高效率，同时兼有波动理论的高反演精度.在有限频理论中，带限地震波的传播能量主要分布在第一菲涅尔带内，我们把加入第一菲涅尔带限定的Frechet核函数称为菲涅尔带层析核函数，并据此提出了菲涅尔带走时层析反演方法.本文首先建立第一菲涅尔带的概念，然后从频率域波动方程的Born与Rytov近似入手，推导菲涅尔层析核函数，通过射线旅行时残差与Rytov近似下的旅行残差的比较，进一步提出了基于Rytov近似旅行时残差的菲涅尔带走时层析方法.最后，将本文的方法应用于表层速度建模中，验证了菲涅尔走时层析较高的计算精度与分辨率.

1 第一菲涅尔带

在菲涅尔带走时层析中，地震波是沿着激发，接收点间的一个类似“管道”的空间传播的，这个传播的空间我们定义为菲涅尔带.如图 1a所示，位于S点的震源激发带限地震波，位于R处的接收点的波场可以表征为波场在SR之间的F面上的积分.理论上的积分波场为全波场，但是在反向散射场远小于入射波场时，可以认为积分波场为入射波场，即Kirchhoff近似.在这种近似下，接收点波场是在F上的不同的点的散射波在接收点R处的叠加，积分路径如图 1a所示.此时离中心射线较近的点的散射波场与直达波基本认为是同相位的，而远离中心射线的点的散射波与直达波则有较大 的相位差别.我们用第一菲涅尔带表征这种远近的差别.根据Spetzler与Snieder(2004)等，第一菲涅尔带定义为

TSP代表震源S到介质任意一点P的旅行时，TRP代表由接受点R到P点的旅行时，TSR为震源S到接受点R的最短旅行时，λ为地震波主频对应的波长.上述旅行时可以通过最短路径射线追踪获得.可以证明在二维情况下n=3/8，三维情况下n=1/2.

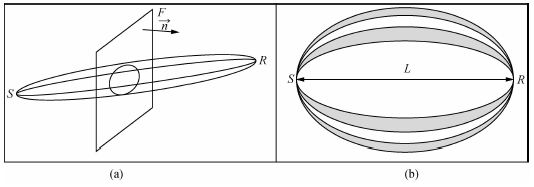图 1 (a)波沿第一菲涅尔带的传播路径；(b)均匀介质中多阶菲涅尔带示意图. Fig. 1 (a)The first Fresnel zone which wave propagates in;(b)Fresnel zones in homogenous media.

在均匀介质中，上式所定义的范围如图 1b中心白色部分所示，其展示了前四个菲涅尔带的分布范围，不同的颜色代表这部分对旅行时产生相反的贡献(Marquering，1998).除第一菲涅尔带之外，相邻的菲涅尔带产生的走时扰动基本相互抵消.因此速度扰动引起的走时扰动主要发生在第一菲涅尔带中.下文中提到的菲涅尔带都是指第一菲涅尔带.

2 菲涅尔层析敏感核函数

传统的射线层析中，利用旅行时残差沿着射线路径进行反投影就可以重建地下速度结构.这个过程表示为

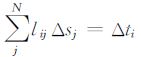这里，Δs(r)为射线路径上r点的慢度扰动，Δt为相应射线的走时扰动量，其离散表达式为，i代表第i条射线，j代表模型第j个网格，lij为i条射线在第j个网格内的射线路径.离散网格内的射线路径组成射线层析核函数，它表明只有射线路径经过的速度扰动才会在接收点引起走时扰动.

根据前面所述，在菲涅尔层析中位于第一菲涅尔带的所有点的速度扰动都会对接收点的走时产生影响，这种影响可以用菲涅尔层析核函数表示.根据层析的基本理论可得

F(r)为菲涅尔层析核函数，Δt为带限地震波走时残差，v，Δv为第一菲涅尔带中介质的速度与速度扰动量.F(r)定量表征了位于第一菲涅尔带中的速度扰动与接收点走时扰动的关系.

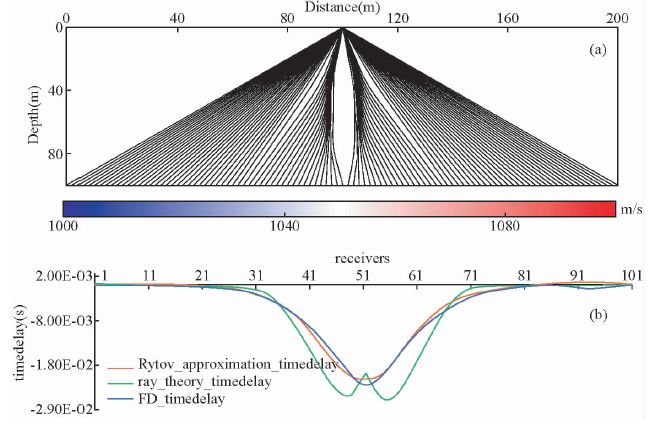图 2 (a)带有异常体速度模型及相应的射线路径；(b)基于左图模型的射线旅行时残差，Rytov近似旅行时残差与基于有限差分波场模拟旅行时残差对比. Fig. 2 The raypaths in the velocity model with two small-scale anomalies(a)，the traveltime delay based on ray-theory，the traveltime delay under Rytov approximation and the traveltime delay based on the wavefield simulation.

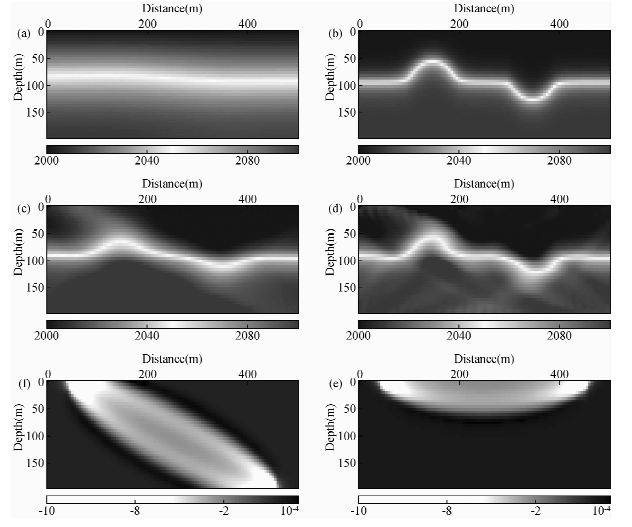图 3 简单模型菲涅尔层析反演结果.
(a)真实模型；(b)初始模型；(c)10次迭代后的更新结果；(d)20次迭代后的更新结果.(e)、(f)不同观测方式单一炮检对带限敏感核函数. Fig. 3 The inverting result for simple model based on Fresnel Zone tomography.
The true model(a)，the initial model(b)，the updated model after 10 iterations(c)，the updated model after 20 iterations(d)，the sensitivity kernels based on the initial model for one source-receiver pair(e)，(f).

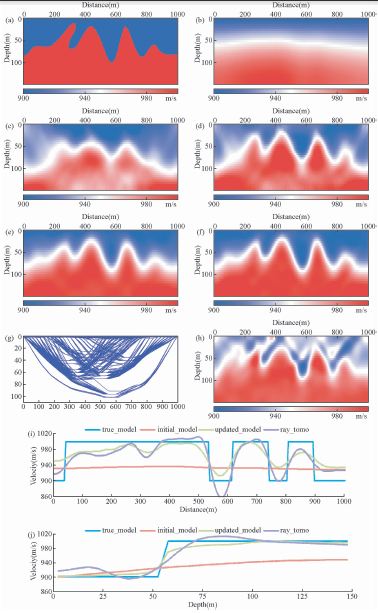图 4 复杂模型菲涅尔层析反演结果
(a)真实模型；(b)初始模型；(c)10次迭代后的更新结果；(d)15次迭代后的更新结果；(e)20次迭代后的更新结果；(f)30次迭代后的更新结果；(g)射线层析迭代30次后的更新结果；(h)射线层析迭代30次后的射线路径；(i)75m深度处，真实模型，初始模型，反演结果的横向速度对比；(j)cdp100处，真实模型，初始模型，反演结果的垂向速度对比. Fig. 4 The inverting result for complicated model based on Fresnel zone tomography
The true model(a)，the initial model(b)，the updated model after 10 iterations(c)，the updated model after 15 iterations(d)，the updated model after 20 iterations(e)，the updated model after 30 iterations(f)，the comparing between true model initial model and updated model along horizontal at the deapth of 75m(g)，the comparing between true model initial model and updated model along veitical at the cdp of 100.

根据Rytov近似与Born近似的关系(Spetzler，001)，我们可知背景波场U0(r)，一阶Born散射场UB(r)与Rytov扰动场UR(r)的关系满足

其中U0与UR如公式(5)所示.

上式中A0为背景波场的振幅，φ0为包含初相位信息的背景波场相位.将公式(5)代入公式(4)两边取对数可以得到走时扰动Δt与Born散射场UB之间的关系为

其中，ω为圆频率，·表示取复数的虚部.

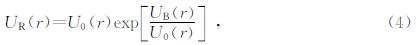
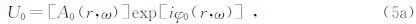
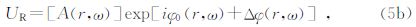
根据Snieder与Lomax(1996)等，Born散射场可以用公式(7)表达为

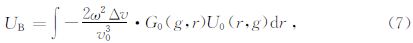
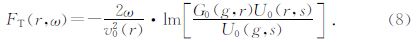
其中，G0 g，r 为无扰动速度场中r点在g处的格林函数.将(7)式代入(6)式，再根据公式(3)即得到单频走时层析核函数表达式(8)：

(8)式即为单频菲涅尔带层析敏感核函数，即可按照经典的层析反演算法，将走时扰动通过核函数反投影到速度场中，即可得到速度更新量.在点源波场的情况下，公式(8)可表示为

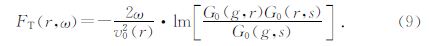
由此可见，核函数求取的关键在于Green函数的求取.考虑到实际地震波是带限的事实，本文采用频率域波动方程求解Green函数，这样可以准确的给出模拟波场的频率，并通过频率的筛选使之与实际数据达到最佳匹配；对于带限地震波，我们沿用Spetzler 与Snieder等的方法对单频菲涅尔带敏感核函数进行加权积分得到带限菲涅尔带层析敏感核函数

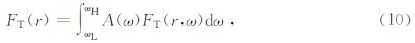
其中ωL，ωH 表示带限地震波频带范围，A(ω)为权系数.权系数可以根据振幅谱或高斯公式计算求得，为方便起见，本文中的权系数根据高斯公式计算得到，其满足条件

3 Rytov近似旅行时残差

传统的射线层析旅行时残差是通过模型正演旅行时与实际观测的旅行时求差获取.实际中，初至旅行时往往淹没在噪声中难以准确拾取，并且射线理论中射线路径存在着聚焦和散焦的现象，从而使射线旅行时求取不准确.而基于Rytov近似下的旅行时残差无需计算观测点旅行时而是直接计算旅行时残差.相对于射线理论而言具有更高的可信度.

根据Snieder与Lomax(1996)，基于Rytov近似下的旅行时残差可以表示为

通过图 2可以看出，相对于射线理论计算的旅行时残差而言，基于Rytov近似下的旅行时残差更接近与有限差分法模拟波场计算的旅行时残差，从图 2a中可以明显看出由于高速异常体引起的射线聚焦现象，使得射线旅行时的求取变得复杂.如图 2b所示，射线理论计算的旅行时残差明显大于基于Rytov近似的旅行时残差，这在后续的反演过程中必然会造成更多的误差.基于Rytov近似的旅行时残差更接近与有限差分法模拟波场计算的旅行时残差，更加准确地刻画了波的实际传播过程.本文设计的模型由于接收点的位置距离异常体并不远，因此射线旅行时残差与Rytov近似旅行时残差，有限差分模拟波场计算的旅行时残差相差不多，波前弥合造成的旅行时残差的消减现象表现的不明显.

4 模型试算

根据公式(9)求出菲涅尔带层析敏感核函数，结合公式(3)建立反演方程，就可以实现速度场的迭代更新.

本文设计的简单模型如图 3所示.模型离散网格为101×40，采样间隔为5×5 m，双层介质，在界面处存在一个高速和一个低速异常体，采用地下激发地面接收的观测系统.波场通过频率域的波动方程求得，共41炮，每炮41道.图 3e、f分别是地面激发地面接收，地下激发地面接收的观测系统得到的一个炮检对的敏感核函数，可以看出相对射线，菲涅尔敏感核函数更大更均匀地覆盖异常体，从而减弱了层析反演矩阵的稀疏性，使反演结果更为稳定；同时菲涅尔敏感核函数精细地刻画了第一菲涅尔带中的空间点对旅行时扰动的不同影响，在中心射线路径上的速度扰动对走时扰动的敏感性不是最大，最大的区域分布在中心射线路径附近的区域.由图 3d可以看出，菲涅尔层析对于高速与低速扰动的反演能力是不同的，根据有限频理论，介质扰动产生的旅行时扰动受到波前弥合效应的影响，而对于高速和低速扰动体，波前弥合效应是不对称的.

本文设计的复杂模型如图 4所示.模型离散网格为201×30，采样间隔为5×5 m，采取地面激发地面接收的观测系统，模型存在一系列复杂的构造，使用中心频率20 Hz的频率域波动方程模拟波场，由此计算的第一菲涅尔带的宽度为75 m.速度场左侧的速度扰动小于第一菲涅尔带的宽度，理论上射线层析无法得到准确的成像效果.从给定初始模型可以看出，基本无法反映速度扰动的分布.图 4f为本文方法的速度反演结果，图 4g，h为传统射线层析反演的结果与相应的射线路径.从迭代结果可以看出，在不依赖较高的初始速度模型的情况下，本文方法准确反演出了速度扰动的位置与大小，而从射线层析的结果可以看出，反演的更新量很不稳定，产生了较多的假象，产生了一些异常值，速度界面的反演结果也不够精确，射线路径覆盖的范围有限且分布不均匀，导致更新的区域不均匀.通过对比可知，本文的方法相对于射线层析成像的结果，优势明显.如图 4g、h所示，对反演结果抽取深度为75 m与cdp=100处的速度曲线进行对比，显示了本文的方法较高的反演精度与分辨率.

5 结 论

本文提出了基于频率域有限差分法的菲涅尔带层析反演方法，该方法可以有效的提高反演的计算精度与效率.相对于射线层析而言，该方法提供了更为可靠、准确的旅行时残差信息，基于Rytov近似的旅行时残差不会受到射线聚焦与散焦的影响.在频率空间域，该方法可以方便的筛选不同的频率范围进行层析，通过这种不同频带的结合可以有效的反演高波数与低波数的速度扰动.该方法摒弃了射线层析的无限高频近似，同时建立了速度扰动与走时残差的线性关系，因此兼有射线层析计算效率高与波动层析无高频假设的优点.模型试算的结果表明，该方法不仅具有较高的反演精度与分辨率，同时拥有较高的反演计算效率.不断提高三维菲涅尔带走时层析的计算效率同时对菲涅尔振幅层析的进一步研究与应用是以后的主要研究方向.在油气勘探日渐复杂的今天，菲涅尔带层析方法必将在实际应用中发挥越来越重要的作用.

致 谢 本研究得到了国家自然基金(批准号：41204086)、国家863课题(2011AA060301)、国家科技重大专项(课题号：2011ZX05006-002)的资助.感谢中国石油大学(华东)物探重点实验室的张凯老师，秦宁博士，桑运云硕士在研究过程中给予的无私帮助和指导.

参考文献
[1] Al-Yahya K.1989. Velocity analysis by interactive profile migration[J].Geophysics,54(6):718-729.
[2] Bian A F, Yu W H, Zhou H W. 2010. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics, 25(3): 982-993.
[3] Bois P, La Porte M, Lavergne M, et al. 1972. Well-to-well seismic measurements[J].Geophysics, 37 (3):471-48.
[4] Dahlen F A, Hung S H, Nolet G.. 2000. Fréchet kernels for finite-frequency traveltimes—I[J]. Theory. Geophysical Journal International, 141: 157-174.
[5] Faye J P, Jeanot J P, Denelle E. 1986. Prestack migration velocities from depth focusing analysis[J]. Expanded Abstracts of the 56th Annual Internat SEG Meeting, 438-440.
[6] Garotta R, Miehon D. 1967. Continuous analysis of the velocity function and of the normal-moveout corrections[J]. Geophysical Prospecting, 15 (4): 584 -597.
[7] Jiang Y, Chen X F. 2011. Review on the comparative study between finite-frequency tomography and ray-theoretical tomography[J]. Progress in Geophysics, 26(5): 1566-1575.
[8] Jin S, Beydoun W. 2000. 2D multiscale non-linear velocity estimation[J]. Geophysical Prospecting, 48(1):163-180.
[9] Jocker J, Spetzler J, Smeulders D, et al. 2006. Validation of First-Order Diffraction Theory for the Traveltimes and Amplitudes of Propagating Waves[J]. Geophysics, 71: 167-177.
[10] Ke B, Zhang J Z, Chen B, et al. 2007. Fat-ray first arrival seismic tomography and its application[J]: 77th Annual International Meeting, SEG, Expanded Abstracts, 3354-3358.
[11] Liu Y Z, Dong L G. 2007. Analysis of influence factors of first-breaks tomography[J]. Oil Geophysical Prospecting,42(5):544-553.
[12] Liu Y. Z, Dong L G, Wang Y W, et al. 2009. Sensitivity kernels for Seismic Fresnel Volume Tomography[J]. Geophysics, 74 (5):U35-U46.
[13] Liu Y Z; Dong L G; Li P M, et al. 2009. Fresnel volume tomography based on the first arrival of the seismic wave[J].Chinese J.Geophys. (in Chinese),52(9): 2310-2320.
[14] Liu Y Z, DONG L G. 2012. Influence of wave front healing on seismic tomography[J]. Sci China Earth Sci, 42(5):784-794.
[15] Luo Y, Schuster G T. 1990. Wave equation traveltime inversion[J]. Expanded Abstracts of the 60th Annual International SEG Meeting,1207-1210.
[16] Marquering H, Nolet G, Dahlen F A. 1998. Three-dimensional waveform sensitivity kernels[J].Geophysical Journal International, 132: 521-534.
[17] Qin N, Li Z C, Yang X D, et al. 2013. Pre-stack joint migration velocity modeling with multi-stage optimization[J]. Progress in Geophysics, (1): 320-328.
[18] Qin N, Li Z C, Zhang K, et al. 2013. Joint tomography inversion of image domain for elastic vector wavefield[J]. Chinese Journal Geophysics,56(9): 3109-3117.
[19] Spetzler G. and Snieder R, 2004. The fresnel volume and transmitted waves[J]. Geophysics, 69, 653-663..
[20] Spetzler G, Snieder R. 2001. The effect of small-scale heterogeneity on the arrival time of waves[J]. Geophysical Journal International, 145: 786-796.
[21] Snieder R, Lomax A. 1996. Wavefield smoothing and the effect of rough velocity perturbations on arrival times and amplitudes[J]. Geophysical Journal International, 125: 796-812.
[22] Xu X M; Shi D N; Li X F. 2009. Research progress of the finite-frequency tomography method[J]. Progress in Geophysics, 24(2): 432-438.
[23] Zhang J Z, Zhao B and Zhou H W. 2009. Fat ray tomography with optimal relaxation factor[J]. Expanded Abstracts of 2009 SEG Annual International Meeting..
[24] Zhang M, Li Z C, Zhang K, et al. 2011. Comparisons and analyses of prestack migration common-image point gathers[J]. Progress in Geophysics, 26(1): 220-228.
[25] Zhang K, Li Z C. 2013. Tomographic velocity inversion method with dual-complexity[J]. Progress in Geophysics, 28(6): 3001-3006.
[26] Zhang Z G, Shen Y, Zhao L. 2007. Finite-frequency sensitivity kernels for head waves[J]. Geophysical Journal International, 171: 847-856
[27] 卞爱飞, 於文辉, 周华伟.2010.频率域全波形反演方法研究进展[J]. 地球物理学进展, 25(3): 982-993.
[28] 江燕, 陈晓非.2011.有限频与射线层析成像比较研究综述[J]. 地球物理学进展, 26(5): 1566-1575.
[29] 刘玉柱,董良国,李培明,等.2009.初至波菲涅尔体地震层析成像[J]. 地球物理学报, 52(9): 2310-2320.
[30] 刘玉柱,董良国.2007.初至波层析影响因素分析[J].石油地球物理勘探, 42(5):544-553.
[31] 刘玉柱,董良国.2012.波前弥合现象对地震层析成像的影响[J].中国科学 地球科学,42(5):784-794.
[32] 秦宁, 李振春, 杨晓东,等. 2013.叠前多级优化联合偏移速度建模[J]. 地球物理学进展, (1): 320-328.
[33] 秦宁, 李振春, 张凯,等. 2013.弹性矢量波成像域联合层析反演[J]. 地球物理学报, 56(9): 3109-3117.
[34] 徐小明;史大年;李信富. 2009.有限频层析成像方法研究进展[J]. 地球物理学进展, 24(2): 432-438.
[35] 张凯, 李振春.2013.双复杂条件下层析速度反演方法研究[J]. 地球物理学进展, 28(6): 3001-3006.
[36] 张敏, 李振春, 张凯, 等. 2011.叠前偏移共成像点道集的对比分析[J]. 地球物理学进展, 26(1): 220-228