2. 中国地质调查局南京地质调查中心, 南京 210016;
3. 中国科学院大地测量与地球物理研究所, 武汉 430077
2. Nanjing Center, China Geological Survey, Nanjing 210016, China;
3. Institute of Geodesy and Geophysics, Chinese Academy of Science, Wuhan 430077, China
盆地沉积层厚度不仅是地质普查、矿产资源调查、油气勘探等必须了解的目标,也是研究地震强地面运动的重要参数.一方面,盆地是油气等资源赋存的重要场所,勘探需求高;但沉积层就像一块毛玻璃一样,使得我们难以看清深部的构造和岩性,严重影响中深目的层的勘探效果.另一方面,沉积层厚度是决定地震灾害的重要因素.由于盆地沉积层与下伏基岩存在较大波阻抗差异,会放大地震波的入射作用,使得强震地面运动持续时间增加,导致沉积盆地上地震灾害加重(Graves et al., 1998).Olsen et al.(1995)模拟发现,地震波在沉积盆地中传播,其振幅是基岩中传播的2.9倍,持续时间是基岩中传播的40倍.Lee et al.(2009)利用谱元法模拟地震波在山间盆地中传播,发现盆地中的峰值地面速度(PGV)可以提高50% 以上.城市和人口密集区大都分布于沉积盆地之上,一旦发生地震,将会造成巨大的人员伤亡和经济损失.例如1985年墨西哥Michoacan地震,虽然距离墨西哥城较远,但由于城市下方分布有厚达数百米的软弱湖积层,对地震波的场地放大致使该城遭受严重毁坏,造成 9000 多人死亡和11 亿美元的经济损失.我国属于地震多发国,地震造成的经济损失和人员伤亡一直位居世界前列(陈棋福等,2008).近几年更是大地震不断,发生了如汶川8.0 级地震和玉树7.1 级地震,造成难以估量的损失.沉积层的厚度及其与基岩的速度差是模拟场地强地面运动的重要参数,研究它有助于评估地震破坏强度(Kawase and Aki, 1989;万志清等,1993).因此,研究盆地沉积层具有十分重要的社会意义.
如何经济、高效的获得盆地沉积层厚度,许多地球物理工作者都在致力于这方面的研究.目前获取近地表结构的方法主要有钻孔测井法、浅层地震勘探、以及面波法.钻孔测井能给出最准确的介质物性参数如波速、密度等,但昂贵耗时且覆盖有限.浅层地震勘探可以给出比较精细的界面分布和速度结构,是目前最为常用的浅层结构勘探手段.但同样勘探成本较高,并且在城市区域实施较为困难.面波法是近年发展起来的一种新的浅层地球物理勘探方法,通过面波频散曲线获得地下介质速度结构,达到划分层位的目的(An and Assumpao,2005; 成锁,2008; 罗艳等,2008).面波法可分为主动源和天然源两大类.主动源面波法是工程物探中主要的探测手段,用于获得 S 波速度结构,但其探测深度较浅;天然源面波法利用天然地震中的面波信息来获得地球内部构造,比较适合大尺度研究.找到一种高效而又能准确探测出沉积层厚度的方法,不仅是地质调查关心的问题,也是地震工程需要解决的.重力勘探具有数据采集效率高的特点,其单点观测一般几十秒到几分钟便能完成,能快速获得区域性的重力数据,进而可以利用沉积层的剩余重力异常反演出它的厚度.
重力勘探是测量与围岩有密度差异的地质体在其周围引起的重力异常﹐以确定这些地质体存在的空间位置﹑大小和形状﹐从而对工作地区的地质构造作出判断的一种地球物理勘探方法.重力从上个世纪三十年代被用于勘探以来,经过几十年的发展,已经取得巨大成就.特别是最近30年,GPS和计算机的发展加速了重力技术在勘探中的应用,重力已成为解决地质问题最好的方法之一.
重力勘探应用范围广泛,既适用于大地构造分区、地壳与上地幔深部构造、区域地质调查等大尺度勘探,也适合探测古墓、溶洞等小尺度目标体(王懋基,1994). 重力勘探的前提是探测目标必须有密度差异,根据密度差异才能提取出目标体的剩余异常.一般沉积层的密度相对基岩较低,体现为重力负异常;凹陷的基岩区被覆盖层充填也引起重力低,这种密度差异是根据重力异常估算基岩埋深最关键的因素.基于这种密度差异,利用重力测量基岩埋深已经取得不少研究成果. 柴玉璞(1981)从理论上导出了反映基岩起伏形态的密度界面函数,给出了由重力异常计算基岩深度的公式,并计算了白洋淀地区的重力异常,与实测曲线吻合.Chakravarthi(1995)推导出了盆地二维竖向阶跃模型的重力表达式,以此计算出洛杉矶盆地最大厚度为9.3 km,与钻孔揭露的最大厚度9.5 km 十分接近.Abbott and Louie(2000)反演了里诺和卡森两座城市下方沉积层的重力剩余异常,发现里诺西边存在厚度1.2 km的沉积层,进而推测该区覆盖层对地震波放大作用最强,为城市规划提供了指导.Bohidar et al.(2001)结合重力和五口水井资料,划分出厚度小于30 m的沉积层,用于寻找沉积层中的含水层.Annecchione et al.(2001)根据重力剩余异常反演了南安大略湖橡树岭冰碛覆盖下的密度分布,获得了基岩埋深,在已知深度点上与地震勘探结果一致.Ardestani and Management(2009)通过重力剩余异常反演出德黑兰某街道的沉积层厚度,指导地铁隧道挖掘.Salcher et al.(2012)利用布格重力异常研究了第四系盆地中的断裂.Lamontagne et al.(2011)利用重力绘制了渥太华的沉积层等厚图,用于评估地震潜在的危害,为城市防震减灾提供了重要的参考依据.这些研究成果表明,利用重力测量方法,可以划分出几十米至数千米的沉积层与基岩界面,应用于地质调查、资源勘探、地震工程、城市规划建设等领域.
近年来,利用重力研究盆地基岩埋深的文章不断增多,但没有得到过系统整理,给欲研究此方向的科研工作者带来不便.本文在系统参阅国内外同行几十年来研究成果的基础上,总结重力测定基岩埋深的方法技术、研究现状及存在问题,并对此研究方向进行了展望.
1 盆地沉积层重力异常正演方法地下介质是连续的,地表观测到的沉积层重力效应是整个沉积层内重力效应的积分.为简化计算,需要将连续沉积层离散化.普遍采用的方法是将沉积层离散为二度或三度体,以实现二维或三维正演.
二维模型通常利用无限延伸的二度棱柱体来近似,即将连续沉积层划分为大量细小平行的棱柱体(图 1).第i个柱体在地表处产生的剩余重力场公式为
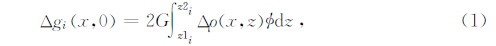

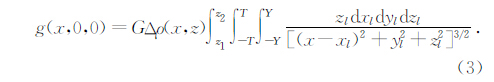
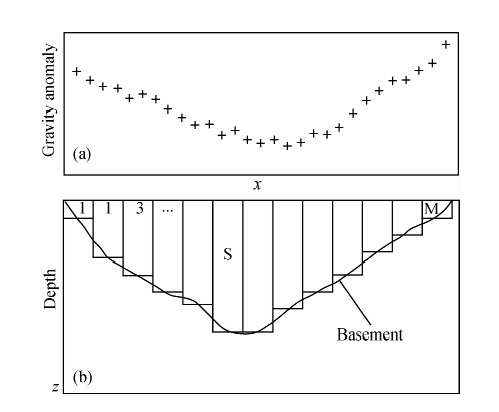 |
图 1 沉积盆地二维离散 (a)盆地沉积层产生的重力异常; (b)沉积层二维离散示意图(Silva et al., 2006). Fig. 1 2-D vertical juxtaposed prism representation of the basin (a)Gravity anomaly produced by a sedimentary basin;(b)The sedimentary of M vertical juxtaposed prisms(Silva et al., 2006). |
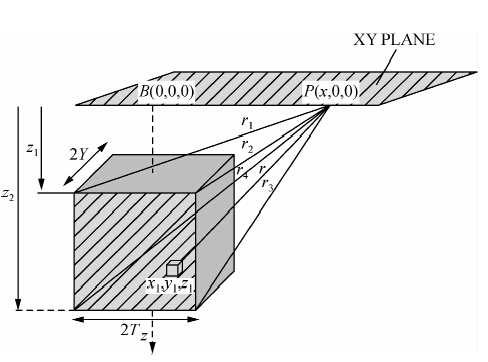 | 图 2 沉积盆地三度体模型(Chakravarthi et al., 2002) Fig. 2 3-D vertical prism and its geometry(Chakravarthi et al., 2002) |
式(1)和式(2)中,G=6.6732×10-11m3kg-1s-2为万有引力常数,下同;Δρ(x,z)表示盆地沉积层(x,z)处的密度与下伏基岩密度的差异,此时计算结果为沉积层的剩余重力异常;为地表观测点到单个柱体两端的夹角,可参考图 3B;z1i、z2i分别表示第i个柱体的底、顶埋深;M为划分的柱体数量.式(3)中,2T为三度体宽度;2Y为三度体走向长度;z1、z2分别表示三度体的顶、底埋深.Athy(1930)观测到盆地上覆沉积物的密度随深度变化而变化,不同的深度相对基岩的密度差异不同.在此基础上,发展出了指数密度函数(Cordell,1973; Radhakrishna Murthy and Bhaskar Rao,1979)、 二次方程密度函数(Rao,1986)、 双曲线密度函数(Litinsky,1989; Sari and Salk, 2002)和抛物线密度函数(Rao et al., 1993)等多种形式.这些表达方式均以沉积层水平方向密度均匀为前提.经过比较,双曲线密度函数和抛物线密度函数更接近沉积层真实密度变化(见图 3),已经得到广泛应用;而指数密度函数和二次方程密度函数难以精确表达盆地沉积层密度差随深度的变化.在可接受的误差范围内,仍有一些研究成果假定沉积层内密度是均匀的,并采用均匀密度差正演计算沉积层产生的重力异常(Bott,1960; Nagy,1966;Banerjee and Das Gupta,1977).
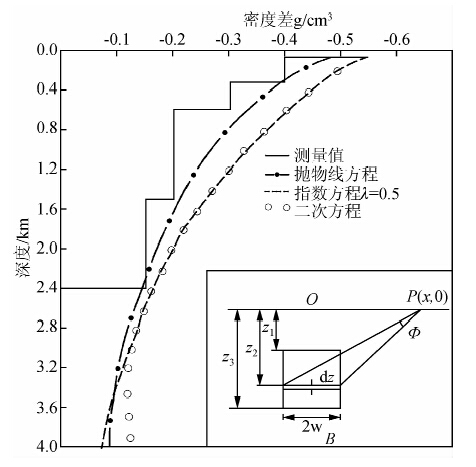 | 图 3 A.密度差函数对比;B.用于计算的柱状模型 Fig. 3 A. Density contrast-depth function by parabolic function,exponential function and quadratic function.B.The prismatic model(Rao et al.,1993) |
抛物线密度函数表达式为


上述密度函数仅考虑了沉积层的密度随深度变化,并假定水平方向密度变化是均匀的.近年来,有人认为地下介质复杂多样,盆地中沉积层的密度不仅在深度上有差异,水平方向的差异也应该考虑(Zhou,2009).
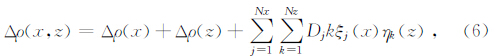
重力测量所获重力场包含了从地表到深部所有密度不均匀引起的重力效应,信息非常丰富(Yegorova and Starostenko, 2002; 曾华霖,2005).因此,地表观测到的重力异常是地下不同深度所有地质体产生的重力效应的叠加,不同地质体引起的异常各有差异.要研究单个目标体,必须进行异常分离,从综合叠加异常中提取目标体产生的剩余异常.然后对剩余异常进行反演,得到目标体的相关参数.地球内部结构十分复杂,各种密度不均匀体形态各异,进行异常分离十分困难.完全分离出沉积层的剩余异常几乎是不可能的,它必定包含其下伏基岩和围岩的重力效应,只能获得某种程度的近似结果.已有成熟的异常分离方法中,盆地研究应用较多的有趋势分析法(Silva et al., 2008;Salcher et al., 2012)、高阶导数法和解析延拓法(Henderson,1960; Leo et al., 1996; Karner et al., 2005)、小波分析法(杨文采等,2001; 杨长保等,2010)及频率域滤波法(Parker,1973; Oldenburg,1974).
趋势分析法是选用一个n阶多项式来拟合整条剖面或整个测区的区域异常,其多项式系数通过最小二乘法确定.观测值与区域异常之差即为剩余异常.多项式阶次的选择应根据区域异常的复杂程度而定,阶次过高或过低都有可能导致区域场面目全非.此方法只能用于测区范围较小且地形地质条件较好的区域.当测区范围较大或地形条件较差时,很难确定一个能有效拟合整个测区的多项式,故不宜使用.高阶导数法根据不同形状地质体的重力异常导数具有不同的特征,利用高阶导数突出浅部地质体异常特征而压制深部区域异常,可划分出不同深度和大小的异常源.解析延拓法分为向上延拓和向下延拓,依据的原理是不同地质体引起的异常衰减和增大速度不同.上延有利于突出深部异常特征,下延突出浅部异常特征.小波分析法具有多尺度分析功能,已经成为重力异常多重分解的重要工具,是重力异常分解的优选.频率域滤波法是根据不同地质体产生的重力异常具有不同的频率进行的.一般而言,深部地质体引起的区域异常具有低频特征,浅部地质体引起的异常具有低频特征.可以通过傅氏变换将时间域观测异常变换到频率域,通过滤波达到异常分离的目的.频率差异越大,分离效果越好.
这些方法都从数学计算层面进行异常分离,每种方法都有适用前提,并非对所有问题都有效果.使用时须具体问题具体分析,针对实际问题选择不同的方法.观测值中不同频率成份的异常相互叠加,仅依靠数学计算分离精度有限.若有先验信息作为参考,则异常分离结果更加可靠.实际工作中往往先验信息有限,只能依据有限的已知信息分离出具有一定精度的剩余异常.Jachens and Moring(1990)提出了一种提取剩余异常的方法:
1)从观测点中挑出位于出露的基岩上面的测点,内插计算出平缓的基岩重力异常Gb. 因为还受到测点周围低密度沉积层的影响,Gb仅为基岩重力场的粗略近似.
2)从观测值Go中减去Gb,得到沉积层的近似剩余异常Gc.利用用公式Gc=2πρ(z)z估算沉积层的厚度z.
3)基岩出露的位置上令z=0,重新计算沉积层的剩余异常Gc,并用于校正Gb.重复上面三个步骤,直到两次Gb之间的误差可以忽略.一般经过6 到10 次迭代便可达到要求.这个方法的关键是具有准确的密度前提.不足之处在于:
1)位于基岩上的测点也会受到附近低密度沉积层的影响,离得越近影响越大;
2)沉积盆地上的观测值随着沉积层的密度变化而变化.两个因素降低了分离结果的精度.
重力异常分离是一个难题,虽然已有多种分离方法,但仍未得到很好的解决,探索新的异常分离方法仍在不断进行中.Leo et al.(1996)以部分孤立的已知点信息(如钻孔)作为先验,采用向下延拓分离沉积层的剩余异常.通过多次迭代计算,获得基岩界面形态.迭代计算过程引入阻尼系数增加了分离方法的可靠性.Golubev等提出利用相关法进行异常分离(Golubev et al., 2002; 郭良辉等,2008). 前提是在一定范围内,若密度分界面起伏平缓或起伏高差远小于界面平均深度,可认为界面引起的重力变化与界面的起伏近似呈线性关系.首先根据观测值用测点坐标的多项式方程拟合区域异常,观测值减去拟合值得到剩余异常,再根据已知测点的基岩埋深反演全区基岩埋深.经理论数据检验,分离效果较好.但考虑到地质条件的复杂性,研究区域很难符合方法的应用前提,还需在实际应用中验证.徐世浙等(2009)提出基于位场分离与延拓的三维视密度反演:
1)利用切割法对平面上的重力场进行不同深度层源的切割分离;
2)运用大深度向下延拓法将各层的场延拓至相应的深度;
3)反演出各深度层的密度,得到各深度层密度的近似分布.该方法不需要解线性方程组,也不需要大量的正演拟合,有效克服了传统方法计算时间特别长、解稳定性差的缺点,实际应用效果也比较好.
从已有研究成果可知,先验信息的准确性十分重要.例如,已知点基岩埋深资料是否准确关系到能否分离出真实的沉积层的剩余异常.已有异常分离方法各有优点和不足,应用时可以先用利用延拓等方法去掉深部区域异常,保留中深部以上的异常,这样做可以减小深部区域异常的影响;然后根据Jachens等提出的方法分离浅部沉积层剩余异常.实际工作中要多选用几种方法,比较分离结果,择优采用.充分利用已知信息方能分离出更接近真实的剩余异常.
3 盆地沉积层的重力反演方法重力反演是定量解释的重要环节.根据剩余重力异常可以反演出沉积层的厚度,获得基岩埋深.定量反演通常将连续的沉积层离散为多个平行柱体(参考图 1、图 2),便于计算.简单的反演方式为
二维迭代反演方法:
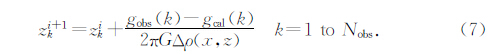
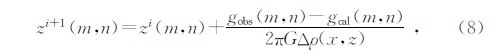
反演是一个非线性问题,直接迭代反演稳定性较差.特别是当盆地基岩起伏剧烈时,难以得到理想的反演结果.Silva 发展了一种更为稳定的非线性反演问题求解方法(Silva et al., 2010):
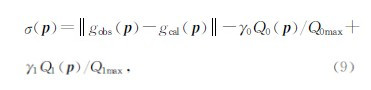
重力场反演具有很强的多解性,不同的密度分布能产生相同的重力场.反演结果的可靠性依赖于重力观测数据的精度和地质模型的准确性,即使采用强约束条件来反演均匀二度体产生的重力异常,也可能产生歧义解.为提高重力反演盆地沉积层精度与可靠性,发展了一些新方法和技术.针对盆地沉积层和基岩起伏研究的重力反演方法有LI-MDR(Line integral and maximum difference reduction)方法(Zhou, 2009,2011)、 近等式约束法(Medeiros and Silva, 1996; Silva et al., 2006)以及联合反演法等.LI-MDR方法计算速度快,对于大面积各向异性的沉积盆地也能得到较好的反演结果.如果基岩最大深度为1000 m,均方根误差能达到10 m.近等式约束法改变单纯的绝对或相对约束方式,基岩出露或钻孔位置采用绝对约束,通过已知点拟合推算出未知点的信息,并将其作为相对约束;这种方法可以避免反演结果局部突变,使反演界面更接近真实形态.
重力非歧义解释依赖于重力以外的信息,如地质、地球物理资料和钻孔等.Aleseev(1993)指出,联合反演可以降低描述参数几何形态的自由度,比单独地球物理资料反演更优越,是地球物理定量解释的重要工具.前面所提的用已知点信息作约束的反演方法都属于联合反演,除此之外,重力还可联合磁法、地震、电法、测井等某一种地球物理方法或多种方法同时联合反演(Babu,1993; 杨辉,1998; 于鹏等,2008; De Castro et al., 2011).
综上所述,反演需要先验信息.除了利用部分钻孔等已知点的信息,若能获得其它地球物理方法资料,建立地质-多种地球物理方法综合模型,使反演过程不只依赖于密度与深度,更能提高反演的可靠性与准确性.
4 国内研究现状国内上世纪八十年代开始利用重力研究盆地沉积层与基岩密度界面.柴玉璞(1981)首先导出了反映基岩起伏形态的密度界面函数,给出了由重力异常计算基岩深度的公式.并计算了白洋淀地区的重力异常,与实测曲线吻合.但该公式只适用于一个密度界面或主要密度界面非常突出的情况.苏达权(1983)利用地震剖面把基底以上的物质层划分为不同密度的层和块,分别用二维多边形近似,计算这些多边形引起的重力值,求出基底以上物质层引起的重力异常,进而推算沉积盆地内的基底密度分布.冯锐等(1989)利用重力研究了华北地区沉积层构造.郝天珧和张岭等(张岭和郝天珧,2006; 郝天珧等,2008)提出利用二维Delaunay 剖分方法,将变密度的二度体分解成若干三角棱柱的组合,求取三角棱柱的重力异常并累加,得到截面为任意形状的水平无限延伸的二度体的重力计算公式.利用该公式正演计算了前新生代残留盆地的浅部重力异常,并联合磁测数据、地震和地质资料反演出前新生代残留盆地宏观分布.该公式加快了重力异常计算速度,但未考虑界面上更多复杂的地质特征,如褶皱、断层、裂缝等.胡卫剑等(2011)利用正、反演方法,分区计算并求取了南海的重力基底,得到了中生界及前中生界残余厚度,据此勾绘了南海海域前新生代残留盆地的分布.黄松等(2010)以同样的方法研究了南黄海的残留盆地分布.王贝贝和郝天珧(2008)采用一种密度界面上已知若干控制点深度的迭代反演方法,对二维单一密度界面的起伏模型进行计算和讨论.并对位于环渤海的黄骅坳陷地区实测剖面进行反演,取得较好效果.
另外一些研究更多的关注密度界面,而不限于沉积盆地,其研究方法和思路值得借鉴.李振海等(2012)提出基于3D Delaunay 剖分算法的重力建模方法,将三维目标地质体分解为若干变密度四面体体元,建立了剩余密度值与重力异常的线性方程组,可用于复杂地质体的重力反演计算.该方法仅应用于理论数据,没有利用实际观测资料进行检验,有待进一步优化.吴招才等(2009)利用三维多层介质模型的地震走时和重力正演公式,推导了地震走时和重力异常对界面深度的雅可比矩阵,实现了三维重力-地震同步联合反演界面成像.利用这些方法也能得到沉积层与基岩的密度界面.
国内重力方法主要以油气、矿产等地质勘探为目的,探测目标较深.城市规划、地震工程等所需浅部信息仍通过地震勘探、高密度电法或钻孔获取.在未来的工作中,一些领域若能更多地考虑引入重力测量方法,可能会起到事半功倍的效果.
5 研究方法的局限性重力方法已经被广泛应用于测定盆地基岩埋深.或用于研究强地面运动,评估地震潜在危害(Lamontagne et al., 2011);或用于地质调查(冯锐等,1989; 郝天珧等,2008; 黄松等,2010; 胡卫剑等,2011);或根据重力研究探测密度界面的方法(王懋基,1994).重力测量结果受很多因素的影响,总结重力方法测定基岩埋深的研究成果,虽然已经取得了一定的成果,但仍存在不足之处.
5.1 重力测量方法的局限性地球物理方法从大的方向可分为重、磁、电、震及放射性等几大类,这些方法本身各有优缺点.电、震可以获得较高分辨率的地质结构,但工作效率低,经济成本高;重、磁获得的是总场,其分辨率较低.重力方法虽可以快速获取大范围与沉积盆地相关的重力异常,进而反演出沉积层的厚度.但受方法本身的影响,测量的密度界面存在一定的误差.特别是在基岩起伏剧烈地区,其误差难以估计.
5.2 异常分离精度仍待提高如果把地球等效于一个鸡蛋,那么沉积层的厚度甚至比蛋壳表面的小薄层还要小.重力测量的是地下不同密度分布物质的总场,岩石的多样性、各种物理化学差异导致地下介质复杂多样.仅仅第四系沉积层就可分为粉土、粘土、粉质粘土、粉砂等多种不同性质的土,加上沉积环境的不同,物性各不相同.因此从观测重力异常中完全分离出沉积层的剩余异常几乎是不可能的,只能近似到一定的程度.异常分离需要结合已知地质或地球物理信息等先验信息,实际工作中已知信息往往有限,影响到剩余异常的可靠性.
5.3 反演的多解性反演是重力资料定量解释的重要过程,但存在很强的多解性.仅仅从数学计算层面对重力异常进行反演是没有意义的,必须结合一定的已知信息.联合反演是目前唯一可信的定量综合地球物理解释技术(杨文采,2002).为了获得可靠的盆地沉积层厚度,仅仅依靠重力和一些孤立点很可能引起歧义解,必须尽可能多的获取其它手段的资料,进行联合反演.最好建立统一的数学-地质-地球物理模型(杨辉等,2002).
6 结 语6.1 重力测量简单易行,效率高,成本低,在区域测量中具有独特的优势.密度是研究地球的重要指标,尤其在地震工程中,密度是地震波和强地面运动研究必不可少的参数.已有研究结果表明,在高精度观测资料和准确的已知信息约束下,利用重力资料测定盆地基岩埋深是可行的,可以获得区域沉积层厚度,用于防震减灾研究,减少地震带来的损失.随着研究的深入,方法技术得到发展和提高,重力将成为地震工程中一个重要的手段.
6.2 尽管利用重力测定基岩埋深已经取得一定的成功,仍存不足之处.首先,重力是区域测量的有利手段,在定量解释中存在先天性不足.因为测量的是总重力场,难以精确的分离出不同介质的剩余异常.其次,钻孔或其它地球物理信息有限,影响地质解释的可靠性.最后,基岩起伏剧烈地区反演方法有待优化,提高反演结果的可靠性.
6.3 国内外学者(王懋基,1994; 管志宁等,2002; Nabighian et al., 2005; 徐亚等,2006;姚长利等,2012)对重力测量方法进行了总结和展望,指出联合其它地质或地球物理资料进行处理解释和提高正反演算法的精确度与稳定性仍是未来重力主要发展方向之一.鉴于盆地基岩起伏及沉积层的重要性,如何经济高效的获取基岩埋深是一项很重要的任务,本研究方向值得进一步深化.
| [1] | Chen H G, Wu J S, Wang J L. 2002. Research in modiied simulated annealing gravity inversion [J]. Journal of Jilin University (Earth Science Edition). (in Chinese), 32(3): 294-298. |
| [2] | Chen J, Wang J L, Wu J S, et al. 2000. Application of improved genetic algorithm to inversion of multi layered density interface [J]. Earth Science-Journal of China University of Geosciences (in Chinese), 25(6): 651-655. |
| [3] | Duan B C, Xu S Z. 1997. A study of the scheme of extending edge in the processing of separating local field from regional field form agnetic gravity anomaly [J]. Journal of Computing Techniques for Geophysical and Geochemical Exploration, 12 (4): 298 -304. |
| [4] | Jiang M, Wang Y X, NABELEK J, et al.The crust and upper mantle structure beneath the Himalaya orogenic belt: the result from local earthquake data analysis[J]. Acta Petrologica Sinica, 24(7): 1509-1516. |
| [5] | Jing R Z, Bao G S,Chen S Q. 2003. A review of the researches for geophysical combinative inversion[J]. Progress in Geophysics, 18(3): 535-540. |
| [6] | Jing X L, Yang C C, Li L. 2003. Adapted simulated annealing algorithm for geophysical problems [J]. Progress in Geophysics, 18(2): 327-330. |
| [7] | Lu X F. 2011. Main Structural interfaces of Sichuan basin obtained from inversions of gravity anomalies through modified very fast simulated annealing method [D] [Master's thesis]. Xi an: Northwest University. |
| [8] | Oldenburg D W. 1974. The inversion and interpretation of gravity anomalies [J]. Geophysics, 39: 526-536. |
| [9] | Parker R L. 1973. The rapid calculation of potential anomalies [J]. Geophysical Journal of the Royal Astronomical Society, 31: 447-455. |
| [10] | Qin J X, Hao T Y, Xu Y, et al. The statistical analysis and the relationship between the tectonic units of the Moho Depth in the South China Sea and Adjacent Areas [J]. Chinese J. Geophys.(In Chinese), 2011, 54 (12): 3171-3183, DOI:3969//j. issn.0001-5733.2011.12.017. |
| [11] | Abbott R E, Louie J N. 2000. Depth to bedrock using gravimetry in the Reno and Carson City, Nevada, area basins[J]. Geophysics, 65(2): 340-350. |
| [12] | An M, Assumpao M S. 2005. Effect of lateral variation and model parameterization on surface wave dispersion inversion to estimate the average shallow structure in the ParanáBasin[J]. Journal of Seismology, 9(4): 449-462. |
| [13] | Annecchione M A, Chouteau M, Keating P. 2001. Gravity interpretation of bedrock topography: the case of the Oak Ridges Moraine, southern Ontario, Canada[J]. Journal of Applied Geophysics, 47(1): 63-81. |
| [14] | Ardestani E V, Management D. 2009. Modeling of bedrock topography in an urban area through micro-gravity data[J]. Journal of the Earth & Space Physics, 35(3): 13-22. |
| [15] | Athy L F. 1930. Density, porosity, and compaction of sedimentary rocks[J]. AAPG Bulletin, 14(1): 1-24. |
| [16] | Babu H V R. 1993. Basement structure of the Cuddapah Basin from gravity anomalies[J]. Tectonophysics, 223(3-4): 411-422. |
| [17] | Banerjee B, Das Gupta S P. 1977. Gravitational attraction of a rectangular parallelepiped[J]. Geophysics, 42(5): 1053-1055. |
| [18] | Bohidar R N, Sullivan J P, Hermance J F. 2001. Delineating depth to bedrock beneath shallow unconfined aquifers: A gravity transect across the Palmer River Basin[J]. Groundwater, 39(5): 729-736. |
| [19] | Bott M H P. 1960. The use of rapid digital computing methods for direct gravity interpretation of sedimentary basins[J]. Geophysical Journal International, 3(1): 63-67. |
| [20] | Chakravarthi V, Raghuram H M, Singh S B. 2002. 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth[J]. Computers & Geosciences, 28(1): 53-57. |
| [21] | Chakravarthi V, Sundararajan N. 2004. Automatic 3-D gravity modeling of sedimentary basins with density contrast varying parabolically with depth[J]. Computers & Geosciences, 30(6): 601-607. |
| [22] | Chakravarthi V. 1995. Gravity interpretation of nonoutcropping sedimentary basins in which the density contrast decreases parabolically with depth[J]. Pure and Applied Geophysics, 145(2): 327-335. |
| [23] | Cordell L. 1973. Gravity analysis using an exponential density-depth function-San Jacinto Graben, California[J]. Geophysics, 38(4): 684-690. |
| [24] | DE Castro D L, Pedrosa N C, Santos F M. 2011. Gravity–geoelectric joint inversion over the Potiguar rift basin, NE Brazil[J]. Journal of Applied Geophysics, 75(3): 431-443. |
| [25] | Golubev N, Pavlov D, Zhdanov M S. 2002. The correlation method of gravity data separation and interpretation[C]//SEG Annual Meeting. Society of Exploration Geophysicists. |
| [26] | Graves R W, Pitarka A, Somerville P G. 1998. Ground-motion amplification in the Santa Monica area: Effects of shallow basin-edge structure[J]. Bulletin of the Seismological Society of America, 85(5): 1224-1242. |
| [27] | Henderson R G. 1960. A comprehensive system of automatic computation in magnetic and gravity interpretation[J]. Geophysics, 25(3): 569-585. |
| [28] | Jachens R C, Moring B C. 1990. MAPS of the thickness of Cenozoic deposits and the isostatic residual gravity over basement for Nevada[R].US Department of the Interior, Geological Survey. |
| [29] | Karner G D, Studinger M, Bell R E. 2005. Gravity anomalies of sedimentary basins and their mechanical implications: Application to the Ross Sea basins, West Antarctica[J]. Earth and Planetary Science Letters, 235(3-4): 577-596. |
| [30] | Kawase H, Aki K. 1989. A study on the response of a soft basin for incident S, P and Rayleigh waves, with special reference to the long duration observed in Mexico City[J]. Bulletin of the Seismological Society of America, 79(5): 1361-1382. |
| [31] | Lamontagne M, Thomas M, Silliker J, et al. 2011. Detailed gravity survey to help seismic microzonation: Mapping the thickness of unconsolidated deposits in Ottawa, Canada[J]. Journal of Applied Geophysics, 75(3): 444-454. |
| [32] | Leo J D, Menezes P T L, Beltro J F, et al. 1996. Gravity inversion of basement relief constrained by the knowledge of depth at isolated points[J]. Geophysics, 61(6): 1702-1714. |
| [33] | Lee S J, Komatitsch D, Huang B S, et al. 2009. Effects of topography on seismic-wave propagation: an example from Northern Taiwan[J]. Bulletin of the Seismological Society of America, 99(1): 314-325. |
| [34] | Litinsky V A. 1989. Concept of effective density: Key to gravity depth determinations for sedimentary basins[J]. Geophysics, 54(11): 1474-1482. |
| [35] | Medeiros W E, Silva J C. 1996. Geophysical inversion using approximate equality constraints[J]. Geophysics, 61(6): 1168-1678. |
| [36] | Radhakrishna Murthy I V, Bhaskar Rao D. 1979. Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth[J]. Geophysics, 44(9): 1525-1530. |
| [37] | Nabighian M N, Ander M E, Grauch V J S, et al. 2005. Historical development of the gravity method in exploration[J]. Geophysics, 70(6): 63-89. |
| [38] | Nagy D. 1966. The gravitational attraction of a right rectangular prism[J]. Geophysics, 31(2): 362-371. |
| [39] | Oldenburg D W. 1974. The inversion and interpretation of gravity anomalies[J]. Geophysics, 39(4): 526-536. |
| [40] | Olsen K B, Pechmann J C, Schuster G T. 1995. Simulation of 3D elastic wave propagation in the Salt Lake Basin[J]. Bulletin of the Seismological Society of America, 85(6): 1688-1710. |
| [41] | Parker R L. 1973. The rapid calculation of potential anomalies[J]. Geophysical Journal of the Royal Astronomical, 31(4): 447-455. |
| [42] | Rao C V, Chakravarthi V, Raju M L. 1993. Parabolic density function in sedimentary basin modelling[J]. Pure and Applied Geophysics, 140(3): 493-501. |
| [43] | Rao D B. 1986. Modelling of sedimentary basins from gravity anomalies with variable density contrast[J]. Geophysical Journal of the Royal Astronomical Society, 84(1): 207-212. |
| [44] | Salcher B C, Meurers B, Smit J, et al. 2012. Strike-slip tectonics and Quaternary basin formation along the Vienna Basin fault system inferred from Bouguer gravity derivatives[J]. Tectonics, 31(3): 1-20. |
| [45] | Sari C, Salk M. 2002. Analysis of gravity anomalies with hyperbolic density contrast: an application to the gravity data of western Anatolia[J]. Journal of the Balkan Geophysical Society, 5(3): 87-96. |
| [46] | Silva J C, Costa D L, Barbosa V F. 2006. Gravity inversion of basement relief and estimation of density contrast variation with depth[J]. Geophysics, 71(5): 51-51. |
| [47] | Silva J C, Oliveira A S, Barbosa V F. 2010. Gravity inversion of 2D basement relief using entropic regularization[J]. Geophysics, 75(3): I29-I29. |
| [48] | Silva J B C, Teixeira W A, Barbosa V C F. 2008. Gravity data as a tool for landfill study[J]. Environmental Geology, 57(4): 749-757. |
| [49] | Yegorova T P, Starostenko V I. 2002. Lithosphere structure of European sedimentary basins from regional three-dimensional gravity modelling[J]. Tectonophysics, 346(1-2): 5-21. |
| [50] | Zhou X B. 2009. General line integrals for gravity anomalies of irregular 2D masses with horizontally and vertically dependent density contrast[J]. Geophysics, 74(2): 1-7. |
| [51] | Zhou X B. 2011. Gravity inversion of 2D bedrock topography for heterogeneous sedimentary basins based on line integral and maximum difference reduction methods[J]. Geophysical Prospecting, 61(1): 220-234. |
| [52] | Aleseev A S. 1993. 联合反演问题解的定量描述及其一般特性[C]. //SEG61届年会论文集. 北京: 石油工业出版社, 595-596. |
| [53] | 柴玉璞. 1981. 根据重力异常计算基岩深度的方法[J]. 石油地球物理勘探, (1): 55-63. |
| [54] | 陈棋福, 刘澜波, 王伟君,等. 2008. 利用地脉动探测北京城区的地震动场地响应[J]. 科学通报, 53(18): 2229-2235. |
| [55] | 成锁. 2008. 近地表调查中的面波方法与利用井资料提高分辨率的技术[博士论文]. 长春: 吉林大学. |
| [56] | 冯锐, 郑书真, 黄桂芳,等. 1989. 华北地区重力场与沉积层构造[J]. 地球物理学报, 32(4): 385-398. |
| [57] | 管志宁, 郝天珧, 姚长利. 2002. 21世纪重力与磁法勘探的展望[J]. 地球物理学进展, 17(2): 237-244. |
| [59] | 郭良辉, 孟小红, 石磊,等. 2008. 重力异常分离的相关法[J]. 地球物理学进展, 23(5): 1425-1430. |
| [60] | 郝天珧, 徐亚, 周立宏,等. 2008. 前新生代残留盆地宏观分布的综合地球物理研究——以大港地区为例[J]. 地球物理学报, 51(2): 491-502. |
| [61] | 胡卫剑, 江为为, 郝天珧,等. 2011. 南海前新生代残留盆地分布综合地球物理研究[J]. 地球物理学报, 54(12): 3315-3324. |
| [62] | 黄松, 郝天珧, 徐亚,等. 2010. 南黄海残留盆地宏观分布特征研究[J]. 地球物理学报, 53(6): 1344-1353. |
| [63] | 李振海, 罗志才, 钟波. 2012. 基于3D Delaunay剖分算法的重力建模与分析[J]. 地球物理学报, 55(7): 2259-2267. |
| [64] | 罗艳, 崇加军, 倪四道,等. 2008. 首都圈地区莫霍面起伏及沉积层厚度[J]. 地球物理学报, 51(4): 1135-1145. |
| [65] | 苏达权. 1983. 利用重力资料推算沉积盆地的基底密度[J]. 石油地球物理勘探, (4): 369-378. |
| [66] | 万志清, 彭一民, 孙进忠. 1993. 埋藏基岩地形对地震波动影响的模拟研究[J]. 地球科学, 18(1): 60-66, 127. |
| [67] | 王贝贝, 郝天珧. 2008. 具有已知深度点的二维单一密度界面的反演[J]. 地球物理学进展, 23(3): 834-838. |
| [68] | 王懋基. 1994. 中国重力勘探的新进展[J]. 地球物理学报, 37(S1): 353-360. |
| [69] | 吴招才, 刘天佑, 高金耀. 2009. 三维多层介质重力-地震同步联合反演[J]. 地球物理学进展, 24(4): 1216-1224. |
| [70] | 徐世浙, 余海龙, 李海侠,等. 2009. 基于位场分离与延拓的视密度反演[J]. 地球物理学报, 52(6): 1592-1598. |
| [71] | 徐亚, 郝天珧, 周立宏,等. 2006. 位场小波变换研究进展[J]. 地球物理学进展, 21(4): 1132-1138. |
| [72] | 杨长保, 刘津怿, 吴燕冈,等. 2010. 二维多尺度离散小波/小波包分析进行重力区域场和局部异常分离的模型分析[J]. 地球物理学进展, 25(3): 1007-1014. |
| [73] | 杨辉. 1998. 重力、地震联合反演基岩密度及综合解释[J]. 石油地球物理勘探, 33(4): 496-502. |
| [74] | 杨辉, 戴世坤, 宋海斌,等. 2002. 综合地球物理联合反演综述[J]. 地球物理学进展, 17(2): 262-271. |
| [75] | 杨文采. 2002. 评地球物理反演的发展趋向[J]. 地学前缘, 9(4): 389-396. |
| [76] | 杨文采, 施志群, 侯遵泽,等. 2001. 离散小波变换与重力异常多重分解[J]. 地球物理学报, 44(4): 534-541. |
| [77] | 姚长利, 李宏伟, 郑元满,等. 2012. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报, 55(6): 2062-2078. |
| [78] | 于鹏, 戴明刚, 王家林,等. 2008. 密度和速度随机分布共网格模型的重力与地震联合反演[J]. 地球物理学报, 51(3): 845-852. |
| [79] | 曾华霖. 2005. 重力场与重力勘探[M]. 北京: 地质出版社: 202-230. |
| [80] | 张岭, 郝天珧. 2006. 基于Delaunay剖分的二维非规则重力建模及重力计算[J]. 地球物理学报, 49(3): 877-884. |
 2014, Vol. 29
2014, Vol. 29

