2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, 100029, China
重力异常的产生与地球内部介质的密度不均匀分布直接相关.重力异常的变化总是记录着由于构造运动作用引起的岩石圈内部变形.重力均衡假说的核心是将岩石圈理解为漂浮在软流圈之上且已达到压力平衡状态的一种介质,而地形的起伏由于重力作用在岩石圈内部将得到补偿,即所谓的有山必有根即“山根”的存在.早期的Airy均衡和Pratt均衡模型都属于这种所谓的局部补偿模式(Local model).后期人们发现在某些区域(如夏威夷岛链)地形没有完全得到补偿,岩石圈的变形行为存在长周期特点,进而提出一种区域均衡模式(Regional model),即弹性板均衡模型.
区域均衡模型认为,在地质时间尺度上(>106 a),主导岩石圈内部变形的力与重力作用密切相关,而在构造演化过程中由于上覆载荷的变化,岩石圈内部变形对负载作用响应,常常可以用一个薄弹性板近似.而弹性板的变形可以用弹性板挠曲方程表示,其中挠曲刚度D=ET3e/12(1-υ2),与杨氏模量E、泊松比υ和有效弹性厚度Te相关.通常岩石圈在受力变形过程中,由于存在一定刚度,因此可以承受一定载荷而不产生对应的“山根”.岩石圈有效弹性厚度(Effective elastic thickness,Te)正是这样一个作为度量岩石圈抗变形能力的一个定量指标,与岩石圈热状态、流变学性质、力学特性等诸多物理因素相关,现在已经广泛应用于研究岩石圈力学结构及动力学过程等诸多领域(付永涛等,2000).
由于岩石圈有效弹性厚度Te是表征其力学强度的一个定量指标,因此,常与地震波速度、热流、电导率、密度、磁化率等一起作为表征岩石圈属性的一种物理参数使用.人们通过对比大洋和大陆岩石圈Te值发现,其值明显小于地震学的地壳和岩石圈厚度.通过对不同构造和地质演化单元计算其岩石圈有效弹性厚度,可以为理解造山带、沉积盆地等地质研究对象的构造演化提供信息参考(付永涛等,2005).
关于重力均衡和岩石圈力学变形行为方面的研究,近年来已经成为岩石圈动力学演化方研究的一个热点.以地震波和GPS手段研究岩石圈变形问题(Zhang et al., 2004; Huang et al., 2007; 石玉涛等,2013),都属于直接地球物理手段.而通过重力均衡机制研究,采用地形和重力异常这两种最基本的地球物理观测量研究岩石圈变形问题也已经被广泛应用(Banks et al., 1977; Forsyth,1985; Lowry et al., 1995; Kaban et al., 1999; Kaban et al., 2003; Kaban et al., 2004; Nair et al., 2012).
谈到均衡补偿机制 (ShiChen et al., 2009),最著名的要属Airy和Pratt的均衡模型假说.但是对于数百或数千公里尺度范围的研究区,更需要考虑的就是岩石圈的力学强度特征,人们常用岩石圈有效弹性厚度来表示岩石圈的力学特性(Watts,2001).近年来随着求取岩石圈有效弹性厚度方法的不断发展和对该参数含义的不断认识,及对岩石圈有效弹性厚度变化历史和演化过程等进一步深入研究,作为表示岩石圈强度的一种代表参数,岩石圈有效弹性厚度的研究正不断得到关注 (BoChen et al., 2013).
而且众多研究者除采用布格或自由空气重力异常与地形之间的关系来估算岩石圈有效弹性厚度值外,还衍生出多种均衡计算模型和方法.而关于这方面的研究进展,从最早相关概念的提出,到后期不断的发展,本文认为主要可以概括为三个阶段:(1)实验重力均衡概念的提出和发展;(2)重力导纳和岩石圈有效弹性厚度指标量的估算;(3)应用有效弹性厚度研究岩石圈力学各向异性特性.本文下面将分三节,分别对应着三个阶段的发展,重点介绍基本原理、模型方法、计算误差等方面内容,并详细概括其理论发展过程及主要里程碑式的应用进展.
1 均衡重力异常与实验均衡方法我们常用的重力异常一般可分为三类,即自由空气重力异常、布格重力异常和均衡重力异常,每种重力异常都具有其自身的地球物理意义.其中,自由空气重力异常反映的是地球实际质量分布与大地椭球体之间的偏差;布格重力异常相对于自由空气重力异常是去掉了大地水准面以上所有质量对重力的影响,反映的是地球内部所有密度不均匀物质分布的异常;而均衡重力异常是在布格重力异常基础上,进一步消除由于重力均衡作用在地壳深部产生补偿界面的影响,当然根据不同的均衡原理和模型,可以算出不同的均衡重力异常.这些异常在大区域重力异常解释中要经常用到.因为,均衡重力异常通常可以被认为是均衡补偿面内所有偏离正常密度分布的异常响应,对均衡重力异常的机理解释方面还有研究表明,均衡异常的变化与构造运动存在密切关系,一些新构造运动形成的造山带,在深部尚未形成均衡补偿前,通常都对应均衡异常高值.而一些活动构造也会引起壳内物质的不均匀分布,常常形成均衡异常梯度带,与强地震活动区对应.
在上述三种异常中,均衡重力异常是要根据地形来计算深部补偿界面形态后才能完成均衡校正量的估计.有关重力均衡补偿机制的认识,一般将地壳或岩石圈看作一种线性时不变系统对各种载荷产生“均衡响应”,类似于一种具有滤波器特性的线性系统,该系统对各种输入(地形、应力、各种载荷)在均衡补偿机制下会产生内部变形,直接的输出结果(均衡响应)就是所谓的重力异常.
关于重力均衡假说的发展,其中实验均衡方法(Dorman et al., 1970)的提出是比较有代表性的,主要思路是将地球看成一种线性系统,地形作为地壳上方的载荷可以被看成是一种信号输入,而地壳或岩石圈对这种输入的响应而产生对应的重力异常.岩石圈或地壳的这种特性可以用一种均衡格林函数(Isostatic Green function)或响应函数(Isostatic response function)来表示,因此,在空间域观测的重力异常则可以表示为地形输入与均衡响应函数的褶积;通过二维Fourier变换可以在频率域中以乘积形式表示.实验均衡方法的提出最早应用于分析美国大陆的重力与地形关系,并计算了相应的均衡重力异常图(Lewis et al., 1970;Dorman et al., 1972).但是实验均衡方法本身仍然与Airy和Pratt均衡一样,属于一种局部均衡模式.不同于点在于该方法是通过反演方式获得一个区域的均衡响应函数,并通过谱方法来提高计算速度和精度.该方法的研究结果也表明岩石圈或地壳对于不同波长质量异常体具有一定的承载能力,这显然是与局部均衡模式相矛盾的.
2 重力导纳与岩石圈有效弹性厚度在之后的研究中,人们提出了一种新的理论框架即区域均衡机制(Banks et al., 1977),这种模型将地球外层岩石圈用一种弹性板近似,并假设这个弹性板在流体表面之上漂浮,该弹性板对于上覆载荷有一定的抗弯强度,其均衡响应函数可以用与弹性板力学及弹性性质相关的参数来表示.区域均衡机制的不同在于,认为岩石圈对不同波长特征的地形载荷具有一定的承载能力,通过引入弹性板模型和用岩石圈有效弹性厚度这个表征其力学特性的物理量,来评价不同构造地区岩石圈的属性特征.
弹性板在受垂向负荷加载后的弯曲变形问题,可以用挠曲方程表示(公式1),由于地形通常可以分解为不同波长特征的分量,因此可以用周期性载荷来表示(Turcotte et al., 2002).
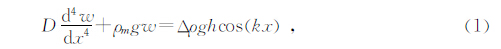
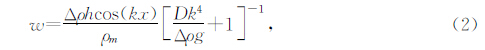
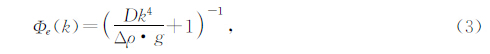
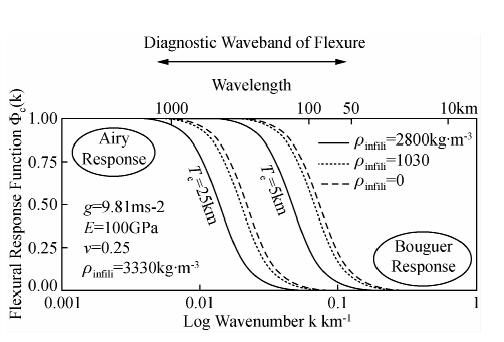 | 图 1 岩石圈挠曲响应函数特性(Watts,2001) Fig. 1 The diagram of lithospheric flexural response function(Watts,2001) |
另一方面,如前所述,均衡学说认为对于岩石圈的均衡响应具有滤波器特性,而由于在频率域中原空间域滤波过程的 褶积运算可以简化为乘积形式,因此,通过在频率域中定义一种重力异常谱与地形谱之比,来引入重力导纳(Gravitational admittance)这个概念,如公式4形式

重力导纳是波数k的函数,由于重力异常和地形都是直接可以观测的物理量,因此,重力导纳可以通过实际观测计算得到.除此之外,对于重力导纳函数的应用,还可以根据不同的均衡模型定义,推导其理论导纳公式,然后再与实际地形谱相乘,得到理论重力异常.在推导理论导纳公式之前,需要应用到位场理论中,频率域密度界面起伏的重力异常表达式(Parker,1972),如公式5所示为
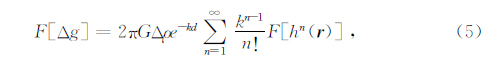
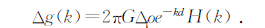
(1)未补偿地形理论导纳公式(D无穷大)
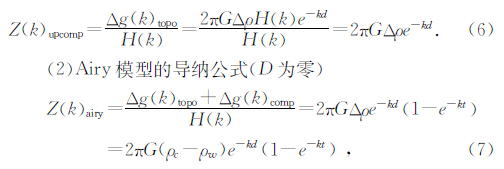
(3)复合模型的导纳公式
在此基础上,对于不同地质构造区域,可以采用不同的均衡研究模型.通常在一些构造活动地区,不但要考虑弹性板之上的地形加载作用,还要考虑弹性板下方一些构造活动引起的反均衡力作用,因此,可以采用如图 2所示复合(板上下加载组合)模式(Forsyth,1985),来表示一些构造活动区域的重力均衡模式.
此时的导纳计算公式为
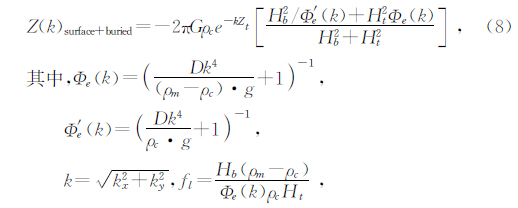
通过以上公式的重力导纳方法,可以在指定岩石圈刚度参数D时,计算重力均衡异常;或者也可以通过实际重力异常与理论计算异常之间的最佳拟合,来估算岩石圈刚度参数D,并进一步计算岩石圈有效弹性厚度Te.
如果在公式8中用
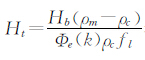
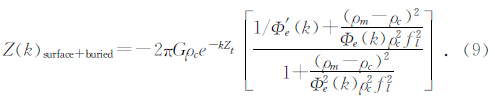
如果我们把现今地表观测到的地形谱如果记为H,则H=Ht+Hb.如果公式9只选择参数的情况下,没有办法对Ht和Hb进行计算,即这两个变量不是独立的.因此,如果要进一步确定或计算这些量,还需要引入另外一个参数r(correlation),定义为

另外,对以上公式中的挠曲刚度D是考虑完全弹性的,如果考虑其粘弹性,可以引入两个参数,即载荷时间t和Maxwell松弛时间τ.这时抗弯刚度Dv,同完全弹性时的抗弯刚度De的关系为
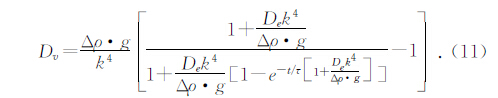
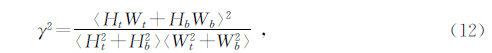
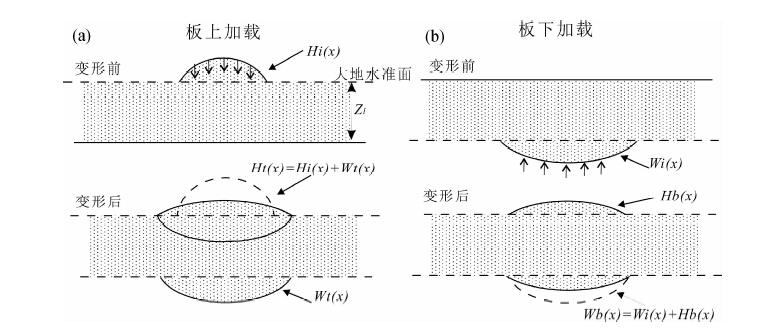 |
图 2 大陆导纳均衡计算复合(Forsyth)模型示意图(Watts,2001) (其中:Zt为地壳厚度,Hi表示变形前变形前板上地形,Wi表示变形前初始变形前等效板下变形,Ht表示变形后由于板上加载剩余的地形,Wt表示变形后板上加载引起的等效板下变形,Wb表示变形后由于板下加载的等效剩余变形,Hb表示由于变形后板下加载引起的板上地形) Fig. 2 The diagram of continental admittance isostasy by Forsyth model(Watts,2001) |
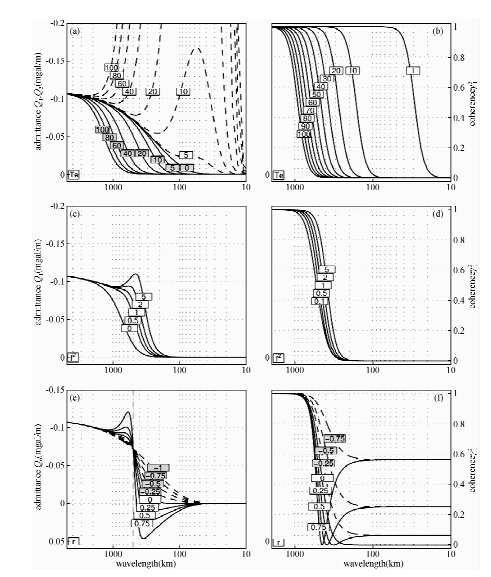 |
图 3 基于复合(Forsyth)模型不同参数的理论重力导纳和相关性曲线(Simons et al., 2013) (其中:上面中a、c、e分别为导纳模型曲线,b、d、f分别为相关函数曲线;图a为不同Te值对应的导纳曲线,b为不同fl值对应的导纳曲线,c为不同r值对应的导纳曲线.图d为不同Te值对应的相关曲线,d为不同fl值对应的相关曲线,f为不同r值对应的相关曲线.其中板厚度为35 km,地壳密度为2670 kgm-3,地幔密度ρm为3300 kgm-3,杨氏模量E=1.4×1011 Pa,泊松比v=0.25) Fig. 3 The gravitational admittance and coherence using Forsyth model with difference parameters(Simons et al., 2013) |
以上理论方法,在参数选择合理时候可以有效地估计岩石圈有效弹性厚度或刚度参数,但是实际应用中,如何选择参数还是经验性的.例如:板上和板下加载变形都是估算的,一般取比值为1.参数选择不合理时,对岩石圈有效弹性厚度估算产生的误差很少被考虑.关于如何优选公式8-10中的三个模型参数,可采用最大似然估计方法(Maximum-likelihood Estimation,MLE)来对Forsyth复合模型计算参数选择的合理性进行估算(Simons et al., 2013).关于重力导纳模型公式原理,如何在区域均衡模式指导下,根据已知地形和重力异常求岩石圈有效弹性厚度的基本思路,已得到全面且详细的阐述(Watts,2001).但是以上模型的假设都是建立在岩石圈有效弹性厚度在空间变化上以各向同性为基础.而近年来发展的各向异性研究技术已渐成为热点.
3 岩石圈有效弹性厚度及力学各向异性根据人们对岩石圈和地幔的研究,通常认为下地幔是近于各向同性的,上地幔存在各向异性特征(Silver et al., 1988).其机理被认为是由于形变导致地幔橄榄岩中的晶格优势排列变化而引起的.最初研究上地幔各向异性的手段,主要来自于地表台站观测到剪切波分裂(SKS)结果.SKS 波能提供很高的横向分辨率,但垂直分辨较差.关于剪切波分裂可以反映的各向异性层深度问题,一直被认为尽管各向异性层可能分布在接收方从核幔边界到接收台站的任何地方,但实际更接近上部.关于岩石圈上部地壳的各向异性,认为主要是由于含流体裂隙或孔隙在应力作用下的定向排列引起的(Silver,1996).
目前研究表明,对大陆地幔各向异性的解释有下列几种:(1)由绝对板块运动引起的各向异性,快波轴方向与绝对板块运动的方向平行;(2)由软流圈中局部的地幔对流引起的各向异性;(3)地壳应力;(4)由过去和现在的构造运动产生的大陆下岩石层中的内部变形(McNamara et al., 1994).
一般认为,快波偏振方向与水平最大主压应力方向一致,通常平行于地表断裂走向或与现今挤压应力场的方向一致.总体上看,岩石圈的各向异性反映了过去和现在的构造运动产生的大陆下岩石层中的内部变形,因此通过各向异性的研究可以推测地球内部物质运动模式.对于稳定大陆地区,各向异性被认为是该区最近一次大规模构造运动遗留在岩石圈中的“化石”各向异性;对于构造运动活跃的大陆地区,各向异性反映了正在进行着的地质构造运动.
相比从剪切波分裂现象中观测到的岩石圈上地幔具有的各向异性特征.人们通过对岩石圈有效弹性厚度的反演结果表明(Simons et al., 2000;Simons et al., 2002,2003; Simons et al., 2003b),在如澳大利亚大陆等一些古老的陆块内部同样岩石圈受力变形也具有一定的方向特性(Simons et al., 2003a).这种性质与岩石圈在均衡作用下的受力变形有关.因此,一般称为力学各向异性,近年来专门针对大陆地区的力学各向异性研究已经开展很多(Simons et al., 2000; Simons et al., 2002,2003a; Simons et al., 2003b; Swain et al., 2003; Audet et al., 2004b,a,2007b; Audet et al., 2007a; Audet,2011; Audet et al., 2011),研究方法和技术也在不断改进.
对这种岩石圈在力学作用下的变形特征研究,开始是通过多窗口谱(Multitaper)方法(MTM),通过计算二维相关函数的方向性变化得到(Simons et al., 2003b).但存在一个窗口大小与结果分辨率之间相互制约的问题.Swain给出了一个正交各向异性材料薄板模型弹性挠曲方程和研究其各向异性的计算方法(Swain et al., 2003).在该正交各向异性材料模型中,D的大小在空间相互正交的方向上具有不同的数值,与取各向同性材料计算不同的是,公式3中的Dk4需要以公式13表示.即
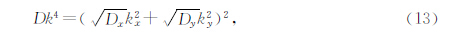
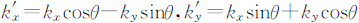
本文通过以上三个部分,从重力均衡学原理及频率域导纳技术入手,概括了近年来从均衡异常计算,到岩石圈有效弹性厚度及力学各向异性等研究成果的重要进展.主要从基本原理和技术发展角度,给出了相关论述.在本节将针对,实际数值计算中的误差来源及近年来相关领域的应用研究情况,做一些总结与展望.
首先,关于岩石圈有效弹性厚度的估算误差问题.第一,应该考虑使用重力异常数据类型,如果我们使用的是布格重力异常,那么对自由空气异常进行地形校正过程中,一定会引入相应的误差;第二,如第2节所述,我们可以定义不同的理论导纳模型,在推导模型公式的推导过程中,是取Parker算法的一阶近似来估算密度界面起伏与重力异常之间关系,因此,高阶项略去同样会引入一定误差;第三,对于不同构造环境的区域,除了弹性板之上的构造加载外,在地壳内部不同深度内也存在一定的板下加载问题,如何定义第2节中组合模型参数问题,即估算内部载荷对均衡补偿机制中的贡献因素,不同参数的选取也会引入一定计算误差;第四,无论是采用何种信号处理技术,都要进行二维相关谱估计,这其中的计算过程也会引入一定的误差.
其次,关于相关领域的研究进展,我国在上世纪90年代就已经关注岩石圈有效弹性厚度的研究问题,在中国大陆王勇等利用相关函数技术,对我国大陆及其邻区的岩石圈强度和补偿机制进行了研究,并且得到了不同构造单元岩石层的有效弹性厚度(王勇等,1996).熊熊等指出对于岩石圈有效弹性厚度显著变化的大陆各地区及块体,只有定量考虑其形变和对重力场的影响,才能客观地了解各种场源的贡献,更合理地分离重力场包含的各岩石层形变分量(熊熊等,1998).
另外,对于一些新生代构造变形强烈地区,如青藏高原的隆升和变形机制也一直是人们长期争论的重要科学问题(滕吉文等,1994).我们知道青藏高原不但存在隆升变形和拉张变形,还伴随着大量内部物质的迁移运动.当前对青藏高原演化模型解释方面,主要围绕岩石圈垂向连续变形观点( Engl and et al., 1982; Flesch et al., 2005)和地壳中存在侧向流体导致了变形随着深度变化(Royden et al., 1997;Clark et al., 2000),这两个模型展开的.前者的主要证据来自于从上地幔剪切波分裂(SKS)结果得到的各向异性方向与GPS记录的岩石圈位移方向一致(Flesch et al., 2005).而后者主要来自于在青藏高原中、下地壳广泛分布的低速层,被认为是管道流模型通道的证据.
上述两种关于岩石圈变形机制的观点,都可以从上地幔各向异性的研究中得到证据.上地幔各向异性研究,对解释板块运动、软流圈对流、地震成因和强震深部背景力源等问题具有重要意义,尤其对青藏高原的隆升演化的动力学过程有特殊意义.从青藏高原地形与布格重力异常之间的关系分析表明(Jin et al., 1994; 陈石等,2011),由于地壳缩短引起的重力均衡补偿,在青藏高原地壳和上地幔之间存在弱的解耦区.对青藏高原东北缘的岩石圈有效弹性厚度和各向异性特性研究表明,阿拉善地块岩石圈变形趋于垂直连贯变形,而柴达木盆地各向异性与历史构造继承性相关,对于松潘-甘孜地块趋于存在侧向物质流动(李永东等,2013).
另外,通过研究中国大陆华南地区对比各向异性Te与地震活动的正相关性,可以说明岩石圈力学性质的各向异性有助于应变集中和在岩石圈中出现脆性破裂.Te的各向异性可以反映大陆岩石圈的构造继承性,同时也是化石应变(Fossil strain)的一种体现(Mao et al., 2012).通过应用Te的各向异性方法,也可以研究我国华北克拉通的构造破坏机制等问题(郑勇等,2012).
综上所述,应用重力异常与地形数据,从最初以计算均衡重力异常为目的的研究.逐步发展到用于估算地壳及岩石圈均衡状态参数,进而发展为通过反演岩石圈有效弹性厚度分布,来研究不同构造演化背景下的岩石圈的力学强度性质.以及通过反演岩石圈有效弹性厚度的各向异性空间分布,进一步开拓了重力异常在研究岩石圈变形过程及历史演化中的应用范围.
致 谢 本文研究过程中得到了美国密苏里大学地质科学系刘勉教授的指导,并与美国普林斯顿大学Simons博士进行了相关讨论,在此一并表示感谢.| [1] | Audet P, Mareschal J C. 2004a. Variations in elastic thickness in the Canadian Shield[J]. Earth and Planetary Science Letters, 226(1-2): 17-31. |
| [2] | Audet P, Mareschal J C. 2004b. Anisotropy of the flexural response of the lithosphere in the Canadian Shield[J]. Geophysical Research Letters, 31: L20601. |
| [3] | Audet P, Jellinek A M, Uno H. 2007. Mechanical controls on the deformation of continents at convergent margins[J]. Earth and Planetary Science Letters, 264(1-2): 151-166. |
| [4] | Audet P, Mareschal J C. 2007. Wavelet analysis of the coherence between Bouguer gravity and topography: application to the elastic thickness anisotropy in the Canadian Shield[J]. Geophysical Journal International, 168(1): 287-298. |
| [5] | Audet P. 2011. Directional wavelet analysis on the sphere: Application to gravity and topography of the terrestrial planets[J]. Journal of Geophysical Research: Planets, 116(E1): E01003, doi: 10.1029/2010JE003710. |
| [6] | Audet P, Burgmann R. 2011. Dominant role of tectonic inheritance in supercontinent cycles[J]. Nature Geosci., 4(3): 184-187. |
| [7] | Banks R J, Parker R L, Huestis S P. 1977. Isostatic Compensation on a Continental Scale: Local Versus Regional Mechanisms[J]. Geophysical Journal International, 51(2): 431-452. |
| [8] | Chen B, Chen C, Kaban M K, et al. 2013. Variations of the effective elastic thickness over China and surroundings and their relation to the lithosphere dynamics[J]. Earth and Planetary Science Letters, 363: 61-72. |
| [9] | Chen S, Wang Q S, Zhu Y Q, et al. 2011. Temporal and spatial features of isostasy anomaly using gravitational admittance model at eastern margin of Tibetan Plateau[J]. Chinese J. Geophys. (in Chinese), 54(1): 22-34. |
| [10] | Chen S, Zhang J, Sun Y J, et al. 2009. Lithospheric thermal isostasy of the north continental margin of South China Sea[J]. Journal of China University of Geosciences, 20(1): 95-106. |
| [11] | Clark M, Royden L H. 2000. Topographic ooze:building the eastern margin of Tibet by lower crustal flow[J]. Geology, 28(8): 703-706. |
| [12] | Dorman L M, Lewis B T R. 1970. Experimental isostasy: 1. Theory of the determination of the Earth's isostatic response to a concentrated load[J]. Journal of Geophysical Research, 75(17): 3357-3365. |
| [13] | Dorman L M, Lewis B T R. 1972. Experimental isostasy: 3. Inversion of the isostatic Green function and lateral density changes[J]. Journal of Geophysical Research, 77(17): 3068-3077. |
| [14] | England P, McKenzie D. 1982. A thin viscous sheet model for continental deformation[J]. Geophysical Journal of the Royal Astronomical Society, 70(2): 295-321. |
| [15] | Flesch L M, Holt W E, Silver P G, et al. 2005. Constraining the extent of crust-mantle coupling in central Asia using GPS, geologic, and shear wave splitting data[J]. Earth and Planetary Science Letters, 238(1-2): 248-268. |
| [16] | Forsyth D W. 1985. Subsurface loading and estimates of the flexural rigidity of continental lithosphere[J]. Journal of Geophysical Research, 90: 12623-12632. |
| [17] | Fu Y T, Li J L, Zhou H, et al. 2000. Comments on the effective elastic thickness of continental lithosphere[J]. Geological Review (in Chinese), 46(2): 149-159. |
| [18] | Fu Y T, Fan S Z, Shi X B. 2005. Geological interpretation of the lithosphere effective elastic thickness [J]. Chinese Journal of Geology (in Chinese), 40(4): 585-593. |
| [19] | Huang Z, Wang L, Xu M, et al. 2007. Shear wave splitting across the Ailao Shan-Red River fault zone, SW China[J]. Geophysical Research Letters, 34(20): L20301. |
| [20] | Jin Y, McNutt M K, Zhu Y. 1994. Evidence from gravity and topography data for folding of Tibet[J]. Nature, 371(6499): 669-674. |
| [21] | Kaban M K, Schwintzer P, Tikhotsky S A. 1999. A global isostatic gravity model of the Earth[J]. Geophys. J. Int., 136(3): 519-536. |
| [22] | Kaban M K, Schwintzer P, Artemieva I M, et al. 2003. Density of the continental roots: compositional and thermal contributions[J]. Earth and Planetary Science Letters, 209(1-2): 53-69. |
| [23] | Kaban M K, Schwintzer P, Reigber C. 2004. A new isostatic model of the lithosphere and gravity field[J]. Journal of Geodesy, 78(6): 368-385. |
| [24] | Kirby J F, Swain C J. 2004. Global and local isostatic coherence from the wavelet transform[J]. Geophysical Research Letters, 31(24): L24608, doi: 10.1029/2004GL021569. |
| [25] | Kirby J F. 2005. Which wavelet best reproduces the Fourier power spectrum?[J]. Computers & Geosciences, 31(7): 846-864. |
| [26] | Kirby J F, Swain C J. 2006. Mapping the mechanical anisotropy of the lithosphere using a 2D wavelet coherence, and its application to Australia[J]. Physics of the Earth and Planetary Interiors, 158(2-4): 122-138. |
| [27] | Kirby J F, Swain C J. 2009. A reassessment of spectral Te estimation in continental interiors: The case of North America[J]. Journal of Geophysical Research: Solid Earth, 114(B8): B08401, doi: 10.1029/2009JB006356. |
| [28] | Kirby J F, Swain C J. 2011. Improving the spatial resolution of effective elastic thickness estimation with the fan wavelet transform[J]. Computers & Geosciences, 37(9): 1345-1354. |
| [29] | Lewis B T R, Dorman L M. 1970. Experimental isostasy: 2. An isostatic model for the U.S.A. derived from gravity and topographic data[J]. Journal of Geophysical Research, 75(17): 3367-3386. |
| [30] | Li Y D, Zheng Y, Xiong X, et al. 2013. Lithospheric effective elastic thickness and its anisotropy in the northeast Qinghai-Tibet plateau[J]. Chinese J. Geophys. (in Chinese), 56(4): 1132-1145. |
| [31] | Lowry A R, Smith R B. 1995. Strength and rheology of the western U.S. Cordillera[J]. Journal of Geophysical Research: Solid Earth, 100(B9): 17947-17963. |
| [32] | Mao X L, Wang Q, Liu S W, et al. 2012. Effective elastic thickness and mechanical anisotropy of South China and surrounding regions[J]. Tectonophysics, 550-553: 47-56. |
| [33] | McNamara D E, Owens T J, Silver P G, et al. 1994. Shear wave anisotropy beneath the Tibetan Plateau[J]. Journal of Geophysical Research: Solid Earth, 99(B7): 13655-13665. |
| [34] | Nair R R, Singh Y, Trivedi D, et al. 2012. Anisotropy in the flexural response of the Indian Shield[J]. Tectonophysics, 532-535: 193-204. |
| [35] | Parker R L. 1972. The rapid calculation of potential anomalies[J]. Geophys. J. Roy. Astron. Soc., 31(4): 447-455. |
| [36] | Royden L H, Burchfiel B C, King R W, et al. 1997. Surface deformation and lower crustal flow in Eastern Tibet[J]. Science, 276(5313): 788-790 |
| [37] | Shi Y T, Gao Y, Zhang Y J, et al. 2013. Shear-wave splitting in the crust in Eastern Songpan-Garzê block, Sichuan-Yunnan block and Western Sichuan Basin[J]. Chinese J. Geophys. (in Chinese), 56(2): 481-494. |
| [38] | Silver P G, Chan W W. 1988. Implications for continental structure and evolution from seismic anisotropy[J]. Nature, 335(6185): 34-39. |
| [39] | Silver P G. 1996. Seismic anisotropy beneath the continents: Probing the depths of geology[J]. Annu. Rev. Earth Planet. Sci., 24: 385-432. |
| [40] | Simons F J, Zuber M T, Korenaga J. 2000. Isostatic response of the Australian lithosphere: Estimation of effective elastic thickness and anisotropy using multitaper spectral analysis[J]. Journal of Geophysical Research: Solid Earth, 105(B8): 19163-19184. |
| [41] | Simons F J, van der Hilst R D. 2002. Age-dependent seismic thickness and mechanical strength of the Australian lithosphere[J]. Geophysical Research Letters, 29(11): 24-1-24-4. |
| [42] | Simons F J, van der Hilst R D. 2003. Seismic and mechanical anisotropy and the past and present deformation of the Australian lithosphere[J]. Earth and Planetary Science Letters, 211(3-4): 271-286. |
| [43] | Simons F J, van der Hilst R D, Zuber M T. 2003. Spatiospectral localization of isostatic coherence anisotropy in Australia and its relation to seismic anisotropy: Implications for lithospheric deformation[J]. Journal of Geophysical Research: Solid Earth, 108(B5), doi: 10.1029/2001JB000704. |
| [44] | Simons F J, Olhede S C. 2013. Maximum-likelihood estimation of lithospheric flexural rigidity, initial-loading fraction and load correlation, under isotropy[J]. Geophys. J. Int., 193(3): 1300-1342. |
| [45] | Swain C J, Kirby J F. 2003. The coherence method using a thin anisotropic elastic plate model[J]. Geophysical Research Letters, 30(19): 2014, doi: 10.1029/2003GL018350. |
| [46] | Teng J W, Yin Z X, Liu H B, et al. 1994. The 2D and 3D lithosphere structure and continental dynamics of Qinghai-Xizhang Plateau[J]. Chinese J. Geophys. (in Chinese), 37(S2): 117-130. |
| [47] | Turcotte D L, Suchubert G. 2002. Geodynamics, 2nd ed[M]. Cambridge, U. K.: Cambridge Univ. Press. |
| [48] | Watts A B. 2001. Isostasy and Flexure of the Lithosphere[M]. New York: Cambridge Univ. Press. |
| [49] | Wang Y, Xu H Z. 1996. The variations of lithospheric flexural strength and isostatic compensation mechanisms beneath the continent of China and vicinity[J]. Chinese J. Geophys. (in Chinese), 39(S1): 105-113. |
| [50] | Xiong X, Xu H Z, Xu J Q, et al. 1998. Dynamic influence of various elastic thickness of continental lithosphere upon lithospheric deformation and Geoid undulation [J]. Crustal Deformation and Earthquake (in Chinese), 18(4): 1-10. |
| [51] | Zhang P Z, Shen Z K, Wang M, et al. 2004. Continuous deformation of the Tibetan Plateau from Global Positioning System data[J]. Geology, 32(9): 809-812. |
| [52] | Zheng Y, Li Y D, Xiong X. 2012. Effective lithospheric thickness and its anisotropy in the North China Craton[J]. Chinese J. Geophys. (in Chinese), 55(11): 3576-3590. |
| [53] | 陈石, 王谦身, 祝意青. 2011. 青藏高原东缘重力导纳模型均衡异常时空特征[J]. 地球物理学报, 54(1): 22-34. |
| [54] | 付永涛, 李继亮, 周辉,等. 2000. 大陆岩石圈有效弹性厚度研究综述[J]. 地质评论, 46(2): 149-159. |
| [55] | 付永涛, 范守志, 施小斌. 2005. 关于岩石圈有效弹性厚度的地质理解[J]. 地质科学, 40(4): 585-593. |
| [56] | 李永东, 郑勇, 熊熊,等. 2013. 青藏高原东北部岩石圈有效弹性厚度及其各向异性[J]. 地球物理学报, 56(4): 1132-1145. |
| [57] | 石玉涛, 高原, 张永久,等. 2013. 松潘—甘孜地块东部、川滇地块北部与四川盆地西部的地壳剪切波分裂[J]. 地球物理学报, 56(2): 481-494. |
| [58] | 滕吉文, 尹周勋, 刘宏兵,等. 1994. 青藏高原岩石层三维和二维结构与大陆动力学[J]. 地球物理学报, 37(S2): 117-130. |
| [59] | 王勇, 许厚泽. 1996. 中国大陆及其邻区岩石层挠曲强度变化和均衡补偿机制[J]. 地球物理学报, 39(S1): 105-113. |
| [60] | 熊熊, 许厚泽, 徐建桥,等. 1998. 大陆弹性岩石层有效弹性厚度对岩石层形变和大地水准面的动力影响[J]. 地壳形变与地震, 18(4): 1-10. |
| [61] | 郑勇, 李永东, 熊熊. 2012. 华北克拉通岩石圈有效弹性厚度及其各向异性[J]. 地球物理学报, 55(11): 3576-3590. |
 2014, Vol. 29
2014, Vol. 29

