2. 天津大学药物科学与技术学院, 天津 300072;
3. 天津大学电气与自动化工程学院, 天津 300072
2. School of Pharmaceutical Science and Technology, Tianjin University, Tianjin 300072, China;
3. School of Electrical Engineering & Automation, Tianjin University, Tianjin 300072, China
0 前 言
不论是声波还是电磁感应以及电磁波,在井眼条件下,由于圆柱边界的影响,井内的响应都是随频率变化的(戈革和谢振全,1980; 张庚骥,1984;别索诺夫,1986;Grant and Phillips, 2010).孔隙地层和裂缝地层,由于物理场在其中传播时,骨架和孔隙流体的相互作用,其声和电参数也是随频率变化的(唐晓明和郑传汉,2004;李巍等,2010;陈雪莲和唐晓明,2012).如果在地面进行测量,电缆的响应也是随频率变化的(关威等,2011;张菊茜等,2011b).所以,最终所测量到的响应频谱是这些随频率变化关系的耦合(Ning et al., 2010;张国艳等,2012;张烨等,2012;卜亚辉等,2013),测井资料处理的目的就是解耦,将耦合在井条件下的地层物理参数随频率的变化关系分离出来,获得地层物理参数随频率的变化关系(Wang and Tang, 2005;陈浩等,2009;姚东华等,2010).
井的影响通常是无法去掉的,因为仪器探头必须通过井才能够下到目的层(尤建军等,2005;刘月萍等,2010;魏宝君等,2011).电缆的影响可以通过在井下设置仪器而消除,但是,仪器外壳会对物理场特别是电磁场又会产生一定的影响(张菊茜,2011a;张菊茜,2011b;吴健等,2013)使问题复杂化.当然,最根本的问题还是如何对频谱的实部和虚部同时进行测量.特别是对虚部的测量,因为地层参数往往包含在虚部信息中(杨健弟等,2007;宋汐瑾等,2009;刘红歧等,2011).
本文介绍声电频谱测井,主要通过现场测井实例和电缆实验结果分析电缆对频谱测井的影响.给出频谱测井曲线中电缆所导致的峰值——我们称其为电缆峰.该峰不但随电缆参数变化,还随探头参数变化(明显);当压电探头从空气进入井内液体后,压电探头参数发生重大变化.因此,声、电频谱测井在套管井中的第一个最简单的应用是下井时可以监测液位,给出准确的液面位置,为采油工程分析地层孔隙压力提供依据.在液位测量过程中,电缆峰的位置变化比较小,与探头的峰变化形成鲜明的对比.
1 声电频谱测井套管井实验结果
为了对声和电频谱测井有一个直观的认识,我们首先给出一组声电频谱测井实例或者实验结果.图 1是声电频谱测井套管井测井实例,与阵列声波测井不同,声电频谱测井测量结果的横坐标是频率,纵坐标是所测量的导纳的实部(电导)和虚部(电纳),单位是毫西门子.为了直观展现声电频谱测井结果,目前现场测井时采用手动方式,每隔100 m停下来测量一次频谱.图 1中每个频谱曲线均按照其相应的深度绘制,每个频谱曲线相差100 m,最下面的曲线是仪器放在地上时测量的导纳曲线,最后的一条曲线为1950 m(目的层)时测量的频谱曲线.
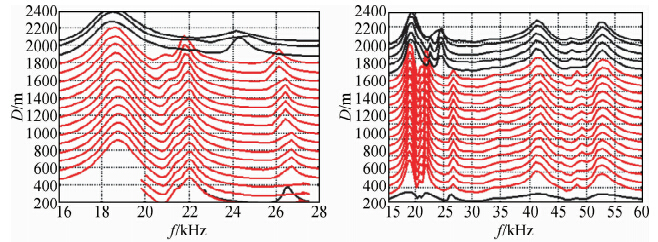 | 图 1 两只相近的声电探头在同一口套管井中测量的频谱曲线 Fig. 1 Frequency spectrum curves of two similar acoustoelectric probes measured in the same cased well |
本次实验所采用的声、电探头由压电陶瓷管和线圈组成.其中压电陶瓷管的谐振频率在20~30 kHz之间,线圈采用双向并绕的方式,抵消线圈之间的互感和对外激发的磁场,主要测量声探头的频率特征.
图 1中有多条黑色的频谱曲线与其它曲线有比较大的差异,最下面的黑色频谱曲线是探头下井前所测量的,最上面的多条黑色频谱曲线是探头进入液面以后测量的.从图 1中可以看出:18~20 kHz区域内有一个幅度比较大的峰值,随着深度的增加,电缆从滚筒上放开进入到井中,电缆的电感量减小,从左图上可以看出:该区域的峰值位置向低频移动.同样,22 kHz位置的峰值也向低频方向移动.26 kHz附近峰值也向低频方向移动.上面3条黑色频谱的峰值位置在18~20 kHz区间内没有什么变化,20~23 kHz位置和26 kHz附近的峰值发生了很大的变化(基本上消失),而在24 kHz附近出现了新的峰值.图 1右图也同样具有这样的情况,进入液面以后,第一个峰值和40~45 kHz、50~55 kHz区间内峰值位置没有多大的变化,而其它峰的位置则发生了很大变化.这些峰值位置变化是由于探头进入液面,声辐射阻抗增加或声负载增加所引起的.对比图 1中探头进入液体前后频谱峰的变化,可以明确:18~20 kHz、40~45 kHz、50~55 kHz区域内的峰是电缆的频谱峰,我们称其为电缆峰,20~27 kHz、45~50 kHz区域附近的峰是探头的频谱峰,我们称其为探头峰.探头峰是声电频谱测井所要测量的峰,与地层声电参数有关.
图 1右图所使用的探头是另外一只与左图同类型的探头.实验前,往井筒里注入了水,改变了液面位置.从图上可以看到:18~20 kHz区域的电缆峰是一直存在的,当探头进入液面以后,电缆峰的形状发生了一定的变化——变粗.
更换另外一种结构的探头进行实验得到如图 2所示的波形.其中右图是所有测量的频谱曲线重叠后的结果.同样,在探头没有进入液体之前,测量到的频谱有三个幅度比较大的峰和一个比较小的峰(位于30~35 kHz),但是,当换能器进入液体以后,这三个峰均消失,只有一个缓慢变化的峰,在其中有一些很小的峰出现.与图 1也有很大的差别.
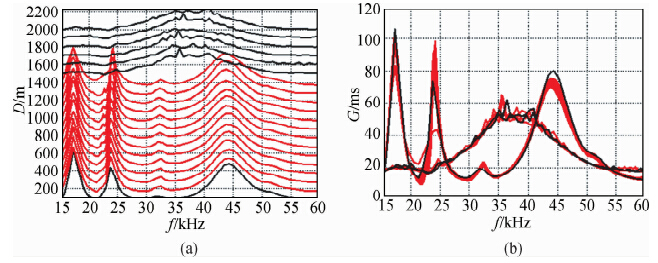 | 图 2 第二种结构的换能器所测量到的频谱曲线,右图是重叠以后的结果 Fig. 2 Frequency spectrum curve measured with transducer of the second structure,result after overlap on the right |
2 电缆实验结果
由于不同的探头在同一口井、用同一个电缆测量时所测量到的频谱响应差别很大,我们专门对电缆进行了实验.实验方法是:将电缆一端分别开路和短路,测量电缆另外一端缆芯与外皮之间的导纳随频率的变化曲线,如图 3所示.在低频端,导纳分别为极大值(短路)和极小值(开路),导纳最大的峰值交替出现;接上声探头后,所测量的电缆另一端的导纳随频率的变化曲线如图 4所示.与图 3比较发现,其电缆峰的位置发生了移动,除此以外,还出现了另外一个峰与电缆的峰非常靠近,这个峰是探头的峰.
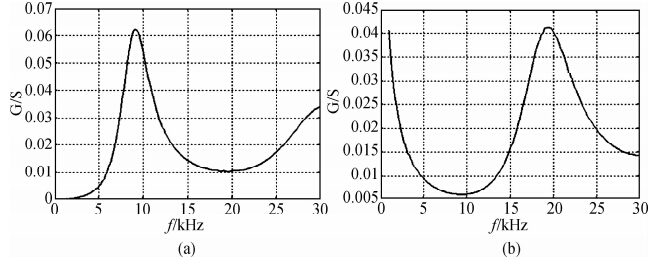 | 图 3 电缆一端开路(左)、短路(右)时在另外一端所测量的导纳随频率的变化曲线 Fig. 3 Changing curve of the admittance along with frequency measured at the other end when one end of cable is open circuit(left figure)or shot circuit(right figure) |
 | 图 4 电缆一端开路(左)、接探头(右)时在另外一端所测量的导纳随频率的变化曲线 Fig. 4 Changing curve of the admittance along with frequency measured at the other end when one end of cable is open circuit(left figure)or connected by probe |
从图 4可以看出:电缆的导纳随频率变化,在一些特殊的频率具有极大值,在另外一些频率具有极小值.随着频率的增加,极大值的峰值减小.
3 电缆模型
图 5所示是电缆接上终端阻抗R以后,任取电缆单元长度δX的等效电路.L是单位长度电感量,C是单位长度电容量,角频率为ω时左端即输入端的等效阻抗Z为:
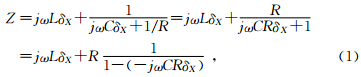
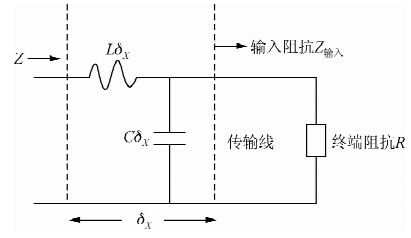 | 图 5 单位长度电缆的等效阻抗与终端阻抗 Fig. 5 Eequivalent impedance of cable of per unit length and terminal impedance |
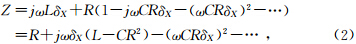
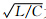 ,则相当于没有电缆的电容和电感的影响,即传输电缆将所有的电能量传输给负载R.我们称这样的效果为负载R与传输电缆匹配,阻抗
,则相当于没有电缆的电容和电感的影响,即传输电缆将所有的电能量传输给负载R.我们称这样的效果为负载R与传输电缆匹配,阻抗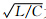 为特征阻抗Z0.它给我们提供了与该电缆匹配的负载的特征.即当负载R等于特征阻抗Z0时,传输电缆能够将高频的电能量全部传输给负载.并且与激发的高频信号的频率无关.
为特征阻抗Z0.它给我们提供了与该电缆匹配的负载的特征.即当负载R等于特征阻抗Z0时,传输电缆能够将高频的电能量全部传输给负载.并且与激发的高频信号的频率无关.
bessonov(1986)给出了正弦波在长度为l的电缆中的传播过程以及在电缆输入端的输入阻抗Zin表达式为
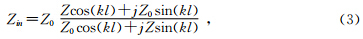
当Z=Z0时,Zin=Z0,这时,电缆对电磁波的传播没有影响.
当cos(kl)=0时,Zin=Z20/Z,这时,电缆相当于阻抗变换器.
当sin(kl)=0时,Zin=Z,这时,电缆对电磁波的传播也没有影响.
该表达式描述了电缆频谱的主要特征,特别是其峰值的位置以及峰值随负载的变化规律,对声电频谱测井具有重要的意义.因为,在声电频谱测井中,声电探头是电缆的负载,负载变化以后,电缆的频谱也随之变化(见图 4峰值位置的差别).在地面仪器即电缆的输入端所接收到频谱也随之变化.这是频谱测井区别于其它测井最主要的一点.
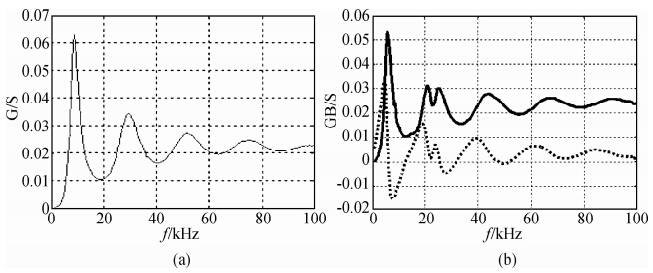
取空气磁导率μ0=4pi10-7亨利/m,空气的介电常数ε0=(8.854185±0.000006)×10-12法拉/m,铠装电缆绝缘材料的相对介电常数ε为2.4,取电缆的特征阻抗Z0=50 Ω;电缆长度l=3200 m,分别取负载电阻为2、20、40和51 Ω时计算电缆的输入阻抗Z得到图 6.从图 6a中可以看到,在第一个虚部为0的位置,频率为15 kHz,阻抗实部的最大值为1250 Ω,与四分之一波长对应的输入电阻相同.从图 6b中可以看到:虚部为0的位置有四个,第一个虚部为0的位置(15 kHz),实部的最大值为125 Ω,第二个虚部为0的位置,实部为20 Ω,与负载电阻相同,即与二分之一波长对应的输入阻抗相同.随着负载阻抗的增加,输入阻抗曲线幅度变小,当负载为50 Ω时,曲线变成了直线,与负载相同,与频率无关,电缆与负载完全匹配.图 2中探头进入液面后其频谱变为平缓的曲线,很多峰消失,说明其阻抗与地层的特征阻抗相近.
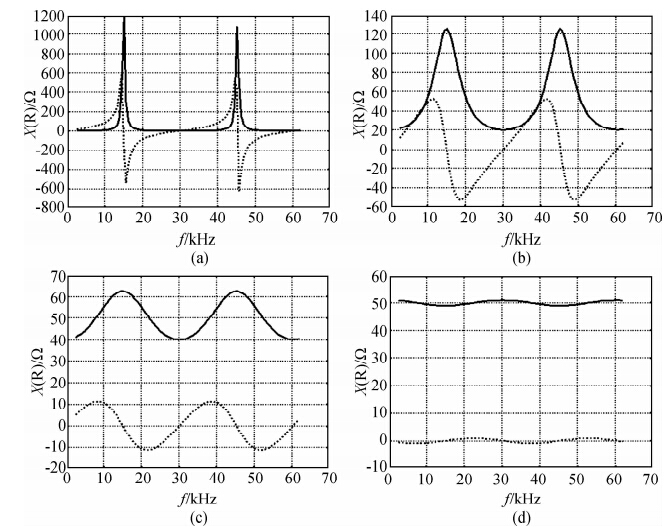 | 图 6 不同负载阻抗时,电缆的输入阻抗随频率的变化关系 (a)Z=2 Ω;(b)Z=20 Ω;(c)Z=40 Ω;(d)Z=51 Ω. Fig. 6 The changes with frequency of the input impedance curve of the cable at different load impedance |
通常情况下,电缆的特征阻抗与负载不一致,电缆的输入阻抗随频率变化.该变化曲线中,有多个频率处虚部为0.这些位置有的对应于四分之一波长,其阻抗很大,有的对应于二分之一波长,其阻抗很小.
探头阻抗的虚部对电缆输入阻抗也有影响,我们取电缆长度为3200 m,分别取Z=5+j*8(虚线)和Z=5-j*8(实线)进行计算得到图 7,左图是电缆输入阻抗的实部(左),右图是虚部(右).从图 7中可以看到:当电缆接容性负载时(对应的阻抗虚部为负),电缆输入阻抗实部最大值所对应的频率增加;当电缆接感性负载时,其对应的频率减小.
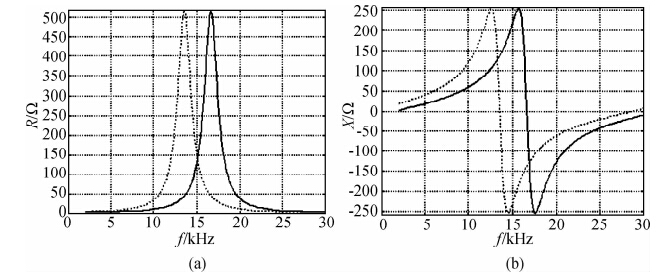 | 图 7 负载阻抗Z的虚部从-8(实线)改变为8(虚线)Ω时,电缆的输入阻抗曲线随频率变化 Fig. 7 The changes with frequency of the input impedance curve of the cable when the imaginary of the load impedance Z changes from -8(solid line)for 8(imaginary line) |
4 分析与讨论
电缆具有分布参数,其影响的结果是:不同频率的正弦波其导纳不同,在频谱曲线上表现为多个峰值,峰和谷的位置与电缆长度有关,对应着半个波长和四分之一波长;也与负载的电抗有关.当电缆确定以后,这些特征基本上是确定的;当负载发生变化时,电缆的峰的位置同样也发生变化.对于频谱测井来讲,当电缆与探头确定后,其频谱的特征基本上是固定的.当电缆从滚筒上放开时,从图 1可以看到:其峰的位置向低频方向有很小的偏移.
对于声波探头来讲,当探头位于空气中(在空井中没有进入液体)时,由于空气的声负载很小,探头的辐射阻抗相应地也很小.这时,探头的谐振频率附近的导纳会比较大,测量的频谱即导纳随频率的变化特征会很明显.如图 1、2中探头没有进入液体前的导纳曲线(红线).
当探头进入液体以后,液体和井筒介质对声波进行反射和透射,这些现象反应到探头上则表现为其辐射阻抗发生巨大改变,最终在探头的导纳上表现为图 1、2中最上面的黑线所示的导纳曲线:探头的谐振频率发生改变,谐振频率处的导纳值发生改变.这些改变后的频谱包含地层参数,从其中提取地层参数或者检测地层参数变化是频谱测井资料处理要解决的问题.
5 结 论
5.1 声、电频谱测井测量探头的导纳或者阻抗随频率变化的曲线,这些曲线包含了井条件下探头的辐射阻抗,辐射阻抗与地层的物理参数有关,通过建立频谱的谐振频率、幅度与地层物理参数的关系,可以从这些测量的频谱中获得地层物理参数的变化规律.现在,频谱测井已经实现,在地面可以直接测量到探头系统的频谱——包括探头导纳的实部和虚部、阻抗的实部和虚部以及模和相角.现场实验结果显示:频谱测井中声探头对井内液体敏感,必须在液体中才能够测量到与地层物理参数有关的辐射阻抗的影响.电缆对测量结果有比较大的影响,但是,这些影响可以通过模型进行刻画,因此,在频谱测井资料处理中可以有效地消除掉.这样,频谱测井作为一种在地面实施测量的测井方法,主要任务是设计探头结构,使其对辐射阻抗灵敏,频谱幅度主要受辐射阻抗影响.这样,便可以最大限度地提高测量信号中地层物理参数信息的含量.使资料处理的难度降低,地层物理参数的测量精度提高.
5.2 从本文提供的实验结果看:第一种探头的峰值比较明显,按照电缆特征阻抗与负载阻抗对电缆输入阻抗的影响(1)式知道:不论是探头在空气中还是进入液面,其负载阻抗 与电缆的特征阻抗Z0均有比较大的差别.第二种探头进入液面后峰值很小说明探头此时的阻抗与电缆的特征阻抗很相近.
致 谢 感谢黑龙江兰德功率超声有限公司提供的帮助.| [1] | Bessonov J A. 1986. Fundamental Theory of Electrical Engineering-the second volume: Nonlinear Circuit and Electromagnetic Field (in Chinese)[M]. Chen W X, Shen L P, Trans. Beijing: Higher Education Press. |
| [2] | Bu Y H, Li A F, Liu J R, et al. 2013. Experimental study on streaming potential influence factors of rock porous media[J]. Well Logging Technology (in Chinese), 37(2): 123-127. |
| [3] | Chen H, Wang X M, Zhao L X. 2009. Study of inversion for third order elastic constants and in situ stress by multifrequency dispersion of cross dipole sonic logging[J]. Chinese J. Geophys. (in Chinese), 52(6): 1663-1674, doi: 10. 3969/j. issn. 0001-5733. 2009. 06. 030. |
| [4] | Chen X L, Tang X M. 2012. Numerical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium[J]. Chinese J. Geophys. (in Chinese), 55(6): 2129-2140, doi: 10. 6038/j. issn. 0001-5733. 2012. 06. 035. |
| [5] | Ge G, Xie Z Q. 1980. Macro Theory of Electromagnetic Field (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [6] | Grant I S, Phillips W R. 2010. Electromagnetics (in Chinese) [M]. Liu Q Y, Wang M Y, Trans. Beijing: People's Education Press. |
| [7] | Guan W, Hu H S, Tang T Z, et al. 2011. The ratio of the acoustoelectric field to the acoustic in a Borehole and its dependence on permeability[J]. Chinese J. Geophys. (in Chinese), 54(6): 1660-1671, doi: 10. 3969/j. issn. 0001-5733. 2011. 06. 026. |
| [8] | Li W, Hu H S, Zhang B X, et al. 2010. Simulation of acoustic well-logging wave field in a radially multilayered fluid-saturated porous formation[J]. Acta Acustica (in Chinese), 35(4): 455-466. |
| [9] | Li X J, Li Z P, Dang R R. 2009. A new method of skin effect correction correction on induction logging[J]. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 31(5): 9-12, doi: 10. 3863/j. issn. 1674-5086. 2009.05.003. |
| [10] | Liu H Q, Deng Y M, Qiu C N, et al. 2011. Research on the characteristic of core permittivity and its application in fluid identification[J]. Journal of Southwest Petroleum University (Science & Technology Edition) (in Chinese), 33(2): 51-54. |
| [11] | Liu Y P, Zheng X K, Li B. 2010. Influence factors analysis of RMT log interpretation accuracy[J]. Well Logging Technology (in Chinese), 34(4): 382-385. |
| [12] | Ning Y, Xiao C N, Richard L, et al. 2010. Simulation of full responses of a triaxial induction tool in a homogeneous biaxial anisotropic formation[J]. Geophysics, 75(2): 101-114. |
| [13] | Tang X M, Zheng C H. 2004. The Quantitative Logging Acoustic (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [14] | Tang X M, 2011. A unified theory for elastic wave propagation through porous media containing cracks-An extension of Biot's poroelastic wave theory[J]. Sci. China Earth Sci. (in Chinese), 41(6): 784-795, doi: 10.1007/s11430-011-4245-7. |
| [15] | Wang T, Tang X M. 2005. Multipole acoustic responses of a prestressed formation: An effective medium approach[J]. Geophysics, 70(2): F35-F44. |
| [16] | Wei B J, Tian K, Zhang X, et al. 2011. Recursive matrix method for simulating response of through-casing resistivity logging[J]. Journal of China of Petroleum (Science &Technology Edition) (in Chinese), 35(6): 59-65, doi: 10. 3969/j. issn. 1673-5005. 2011.06.009. |
| [17] | Wu J, Hu X Y, He S L, et al. 2013. Influence factor analysis and evaluation of LWD curves[J]. Progress in Geophys. (in Chinese), 28(5): 42-2650, doi: 10.6038/pg20130545. |
| [18] | Yang J D, Li J M, Yang G H, et al. 2007. A digital high resolution induction logging tool[J]. Well Logging Technology (in Chinese), 31(4): 360-363. |
| [19] | Yao D H, Wang H N, Yang S W, et al. 2010. Study on the responses of multi-component Induction logging tool in layered orthorhombic anisotropy formations by using propagator matrix method[J]. Chinese J. Geophys. (in Chinese), 53(12): 3026-3037, doi: 10.3969/j. issn. 0001-5733. 2010.12.028. |
| [20] | You J J, Zhang C M, Chen X, et al. 2005. The principle of CHFR Logging and it's influence factors[J]. Progress in Geophysics (in Chinese), 20(3): 780-785. |
| [21] | Zhang G J. 1984. Electrical Logging (in Chinese) [M]. Beijing: Petroleum Industry Press. |
| [22] | Zhang G Y, Xiao J Q, Hao Y J. 2012. Numerical computation and theoretical analysis of three-dimensional induction logging tool [J]. Well Logging Technology (in Chinese), 36(1): 15-19. |
| [23] | Zhang J Q, Chen W, Meng Y X, et al. 2011a. Appliacion of time domain equalizer in the logging cable transmission system[J]. Well Logging Technology (in Chinese), 35(2): 192-194. |
| [24] | Zhang J Q, Chen W, Meng Y X, et al. 2011b. Application of digital echo cancellation technology to logging cable transmission system[J]. Well Logging Technology (in Chinese), 2011, 35(3): 281-283. |
| [25] | Zhang Y, Wang H Z, Tao H G, et al. 2012. Finite volume algorithm to simulate 3D responses of multi-component induction tools in inhomogeneous anisotropic formation based on coupled scalar-vector potentials[J]. Chinese J. Geophys. (in Chinese), 55(6): 2141-2151, doi: 10. 6038/j. issn. 0001-5733. 2012. 06.036. |
| [26] | 卜亚辉, 李爱芬, 刘均荣,等. 2013. 岩石介质流动电位影响因素实验研究[J]. 测井仪器, 37(2): 123-127. |
| [27] | 陈浩, 王秀明, 赵立新. 2009. 交叉偶极子声测井多频率反演地层三阶弹性常数和地应力研究[J]. 地球物理学报, 52(6): 1663-1674, doi: 10.3969/j.issn.0001-5733.2009.06.030. |
| [28] | 陈雪莲, 唐晓明. 2012. 孔、裂隙并存地层中的声波测井理论及多极子声场特征[J]. 地球物理学报, 55(6): 2129-2140, doi: 10.6038/j.issn.0001-5733.2012.06.035. |
| [29] | 戈革, 谢振全. 1980. 宏观电磁场论[M]. 北京: 石油工业出版社. |
| [30] | 关威, 胡恒山, 汤天知,等. 2011. 声电效应测井电声比及其与地层渗透率的关系[J]. 地球物理学报, 54(6): 1660-1671, doi: 10.3969/j.issn.0001-5733.2011.06.026. |
| [31] | 格瑞德, 菲利普斯. 1980. 电磁学[M]. 刘岐元, 王鸣阳译. 北京: 人民教育出版社. |
| [32] | 别索诺夫. 1986. 电工理论基础(下册: 非线性电路与电磁场)[M]. 陈伟鑫, 沈丽英译. 北京: 高等教育出版社. |
| [33] | 李巍, 胡恒山, 张碧星,等. 2010. 柱面分层流体饱和孔隙地层中的声波测井波场模拟[J]. 声学学报, 35(4): 455-466. |
| [34] | 宋汐瑾, 李利品, 党瑞荣. 2009. 一种感应测井趋肤效应校正的新方法[J]. 西南石油大学学报(自然科学版), 31(5): 9-12, doi: 10.3863/j.issn.1674-5086.2009.05.003. |
| [35] | 刘红歧, 邓友明, 邱春宁,等. 2011. 岩芯电容率特征研究及其在流体识别中的应用[J]. 西南石油大学学报(自然科学版), 33(2): 51-54. |
| [36] | 刘月萍, 郑希科, 李波. 2010. 影响RMT测井解释准确度的因素分析[J]. 测井技术, 34(4): 382-385. |
| [37] | 唐晓明, 郑传汉. 2004. 定量测井声学[M]. 北京: 石油工业出版社. |
| [38] | 唐晓明. 2011. 含孔隙、裂隙介质弹性波动的统一理论—Biot理论的推广[J]. 中国科学: 地球科学, 41(6): 784-795, doi: 10.1007/ s11430-011-4245-7. |
| [39] | 魏宝君, 田坤, 张旭,等. 2011. 模拟过套管电阻率测井响应的递推矩阵方法[J]. 中国石油大学学报(自然科学版), 35(6): 59-65, doi: 10.3969/j.issn.1673-5005.2011.06.009. |
| [40] | 吴健, 胡向阳, 何胜林,等. 2013. 随钻测井曲线影响因素分析与评价[J]. 地球物理学进展, 28(5): 42-2650, doi: 10.6038/pg20130545. |
| [41] | 杨健弟, 李娇蔓, 杨国华,等. 2007. 一种数字高分辨率感应测井仪[J]. 测井技术, 31(4): 360-363. |
| [42] | 姚东华, 汪宏年, 杨守文,等. 2010. 用传播矩阵法研究层状正交各向异性地层中多分量感应测井响应[J]. 地球物理学报, 53(12): 3026-3037, doi: 10.3969/j.issn.0001-5733.2010.12.028. |
| [43] | 尤建军, 张超谟, 陈详,等. 2005. CHFR测井原理及影响因素研究[J]. 地球物理学进展, 20(3): 780-785. |
| [44] | 张庚骥. 1984. 电法测井[M]. 北京: 石油工业出版社. |
| [45] | 张国艳, 肖加奇, 郝永杰. 2012. 三维感应测井数值计算与理论分析[J]. 测井技术, 36(1): 15-19. |
| [46] | 张菊茜, 陈伟, 孟悦新,等. 2011a. 时域均衡器在测井电缆传输系统中的应用[J]. 测井技术, 35(2): 192-194. |
| [47] | 张菊茜, 陈伟, 孟悦新,等. 2011b. 数字回音消除技术在测井电缆传输系统中的应用[J]. 测井技术, 2011, 35(3): 281-283. |
| [48] | 张烨, 汪宏年, 陶宏根,等. 2012. 基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应[J]. 地球物理学报, 55(6): 2141-2151, doi: 10. 6038/j. issn. 0001-5733. 2012. 06.036. |
 2014, Vol. 29
2014, Vol. 29


