2. 武汉地震工程研究院, 武汉 430071;
3. 中国地质大学(武汉), 武汉 430074
2. Wuhan Institute of Earthquake Engineering, Wuhan 430071, China;
3. China University of Geosciences(Wuhan), Wuhan 430074, China
0 引 言
活动断层作为构造地质学的术语是20世纪初由A.C. Lawson 最先提出,它以错断第四系为标志.按照国家地震局震害防御司规定:“活动断层是指第四纪期间,尤其是晚更新世(10万年)以来活动过,并在今后仍有可能活动的断层.由于活动断层是地震灾害产生以及造成破坏的主要根源,活动断层探测成为了减轻地震灾害开展的一项重要工作,它的目的是准确查明地表附近活动断层的空间分布,为活动断层的地震危险性评价提供依据(丁国瑜等,1993).由于活动断层往往在地表不易观测到,仅仅依靠地质工作已不能对断层定位和活动性进行全面评价,因此利用地球物理方法探测活动断层具有明显的优势.高密度电法作为其中的一种,被广泛应用于破碎带调查中,并取得了良好的效果(李征西等,2005;易兵等,2005;吴子泉等,2005;吴子泉和尹成,2007;易兵等,2008;王启军等,2009;陈玉玲,2013).
随着正反演技术的发展,为我们更直观的了解高密度电法各装置的探测效果提供了方便.有限元作为电阻率正演常用的方法之一,是Coggon(1971)最早将其应用到求解电磁场问题中去.在电阻率反演方面,应用比较成功的是基于光滑约束的最小二乘反演(Constable et al., 1987;Sasaki,1989;Sasaki,1994;宛新林,2005;范翠松,2013).虽然高密度电法的正反演技术已经有了很好的发展,但未从理论模拟与实例应用方面开展高密度不同装置对活动断层响应特征的系统分析研究.本文通过有限元正演模拟以及最小二乘反演,针对不同电性特点的典型活动断层地层结构模型,探讨各装置的探测效果及有效性,并进行了实例探测分析.
1 基本原理 1.1 有限元正演
高密度电法是利用地下介质的导电性差异,研究人工建立的电场在地下的分布规律.此次高密度电法正演采用的是有限元法,首先基于位和场的偏微分方程,将电位的微分方程转化为泛函的极值问题(泛函的变分问题)去求解.根据电场所满足的微分方程以及边界条件,相应的变分问题为(刘斌等,2010):
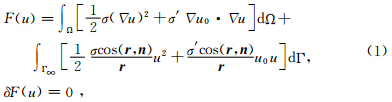
在建立相应的变分方程以后,离散化连续的求解区,即按一定的规则将求解区域剖分为一些在节点处相互连接的网格单元;进而在各单元上近似地将变分方程离散化,并通过单元分析和总体合成,导出以各节点电位值为变量的高阶线性方程组;最后解此方程组,再通过反傅里叶变换算出各节点的电位值,得到地下半空间场的分布,以表征稳定电流场的空间分布.
1.2 最小二乘反演
最小二乘反演作为地球物理反演最常用的方法,它对地球物理资料反演具有很好的稳定性和适应性.最小二乘反演问题可以表示为求使目标函数Ψ极小时的最优模型参数改正值矢量Δ m .为了解决反演问题常常表现出的混定问题,将光滑约束引入反演方程.施加光滑约束后的目标函数Ψ为(刘斌等,2012):
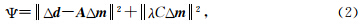
给定初始模型m 0,将上述目标函数对Δ m 求导并令其等于0,可得到如下的线性方程组为
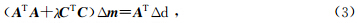

2 理论模拟与分析
为了说明在活动断层调查中高密度电法的有效性、各高密度装置的探测效果,首先通过有限元正演和最小二乘反演从理论模拟方面进行了分析.
2.1 模型设计
考虑到常见地层结构和电性特点,设计了四个由四层层状均匀电性介质和一条断层构成的理论地质模型(模型Ⅰ、Ⅱ、Ⅲ、Ⅳ),第一层为表层(如回填土等)、第二层为第四系层、第三层为风化层、第四层为基岩,断层附存破碎带,倾角均为38.66°,具体参数如表 1和图 1所示.
|
|
表 1 理论地质模型参数表 Table 1 Parameters of theoretical geological model |
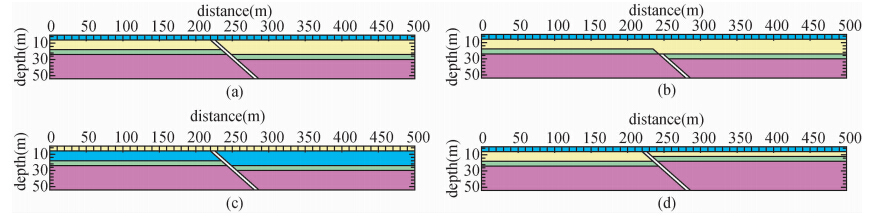 | 图 1 断层理论模型 (a)正断层模型Ⅰ;(b)正断层模型Ⅱ;(c)正断层模型Ⅲ;(d)逆断层模型Ⅳ. Fig. 1 Theoretical fault model (a)Normal fault model Ⅰ;(b)Normal fault model Ⅱ;(c)Normal fault model Ⅲ;(d)Reverse fault model Ⅳ. |
模型模拟计算时均采用有限元法进行正演计算,且电极数为101个、电极距为5.0 m、横向网格数为200个(即网格大小为2.5 m)和纵向网格数为32个(1~2网格大小为0.25 m,3~5网格大小为0.5 m,6~7网格大小为1.0 m,8~32网格大小为2.0 m).以及均采用最小二乘法反演.
2.2 模型Ⅰ不同装置的正反演模拟结果
为了说明活动断层的高密度法的响应特征,对模型Ⅰ进行了常见的几种装置(即温纳、二极、偶极—偶极、三极和温施)的正反演模拟,其正反演模拟结果如图 2所示.图 2a为温纳装置模拟结果,可见视电阻率断面在断层处视电阻率有变化,反演电阻率断面有明显显示,且穿过了覆盖层,基本可识别断层的性质,并且可进行地质分层,但断层深部反映不明显和层内电阻率明显存在横向不均匀现象.图 2b为二极装置模拟结果,可见视电阻率断面在断层处视电阻率有变化,反演电阻率断面有明显显示,断层明显穿过了覆盖层,基本可识别断层的性质,并且可进行地质分层,断层深部反映和层内电阻率均匀性比温纳装置有所改善.图 2c为偶极—偶极装置模拟结果,可见视电阻率断面在断层处视电阻率有明显变化,反演电阻率断面有明显显示,断层明显穿过了覆盖层,基本可识别断层的性质,并且可有效进行地质分层,断层深部反映和层内电阻率均匀性比二极装置得到进一步改善,反演结果与模型基本相符.图 2d为三极装置模拟结果,可见视电阻率断面在断层处视电阻率有明显变化,反演电阻率断面有明显显示,断层明显穿过了覆盖层,基本可识别断层的性质,并且可进行地质分层,断层深部反映和层内电阻率均匀性比二极装置有所改善,反演结果与模型基本相符,但层内电阻率均匀性不如偶极—偶极装置.图 2e为温施装置模拟结果,可见视电阻率断面在断层处视电阻率有明显变化,反演电阻率断面有明显显示,断层明显穿过了覆盖层,基本可识别断层的性质,并且仍可进行地质分层,断层深部反映与温纳装置相当,层内电阻率均匀性与三极装置相当.
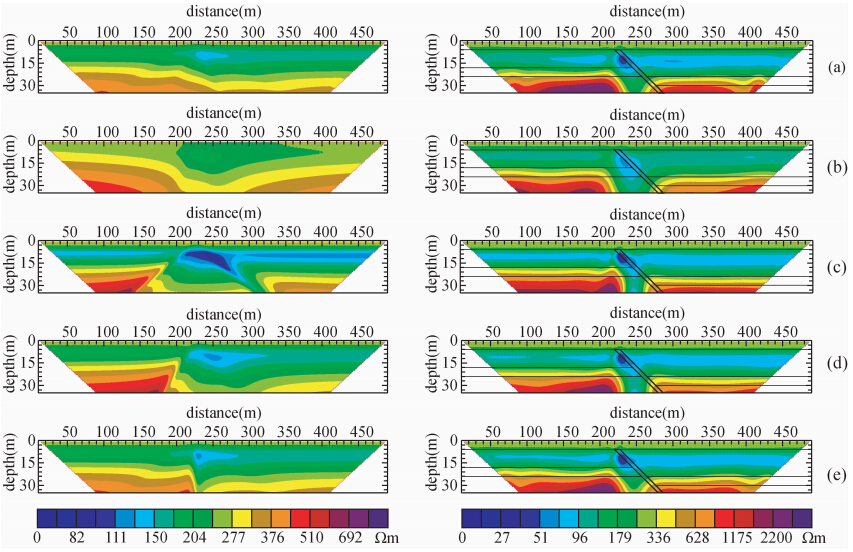 | 图 2 理论模型Ⅰ不同装置的正反演结果图 (a)温纳装置;(b)二极装置;(c)偶极—偶极装置;(d)三极装置;(e)温施装置. Fig. 2 Forward and inversion results with different devices of model Ⅰ (a)Wenner device;(b)Two-pole device;(c)Dipole-dipole device;(d)Three-pole device;(e)Wenner-schlumberger device. |
上述模拟结果表明各装置均可进行表层为高阻层情况下活动正断层的定性探测和地质分层,断层明显穿过了覆盖层,是作为推断断层活动的依据,基本上可定性确定断层的性质,但不能准确获取断层的倾角.相对而言偶极—偶极装置最有效,三极装置次之.
2.3 模型Ⅱ、Ⅲ和Ⅳ的正反演模拟结果
为了进一步说明偶极—偶极和三极两种装置的有效性,进行了表层为高阻层情况下非活动正断层模型Ⅱ、表层为低阻层情况下活动正断层模型Ⅲ和表层为高阻层情况下活动逆断层模型Ⅳ的正反演模拟与响应特征分析.
2.3.1 表层为高阻层情况下的非活动正断层模型
图 3是表层仍为高阻层情况下的非活动正断层模型Ⅱ的偶极—偶极和三极两种装置的正反演模拟结果,可见视电阻率断面和反演电阻率断面均在断层处有明显显示,断层明显未穿过覆盖层,是作为推断断层不活动的依据,基本可定性确定断层的性质,且可有效进行地质分层,但不能有效获取断层的倾角.同样,偶极—偶极装置的反演各层的电阻率精度仍高于三极装置的反演结果,且更有利于进行地质分层.
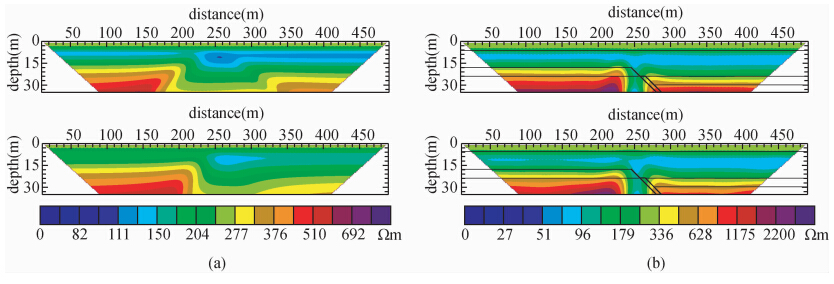 | 图 3 理论模型Ⅱ两种不同装置的正反结果图 (a)偶极—偶极装置;(b)三极装置. Fig. 3 Forward and inversion results with two different devices of model Ⅱ (a)Dipole-dipole device;(b)Three-pole device. |
2.3.2 表层为低阻层情况下的活动正断层模型
图 4是表层为低阻层情况下的活动正断层模型Ⅲ的偶极—偶极和三极两种装置的正反演模拟结果,可见视电阻率断面和反演电阻率断面均在断层处有明显显示,断层明显穿过覆盖层,仍是作为推断断层活动的依据,基本可定性确定断层的性质,且仍可进行地质分层,但不能有效获取断层的倾角和反演各层的电阻率精度比表层为高阻层情况下模型的有所降低,尤其是三极装置的反演结果.同样,偶极—偶极装置的反演各层的电阻率精度仍高于三极装置的反演结果.
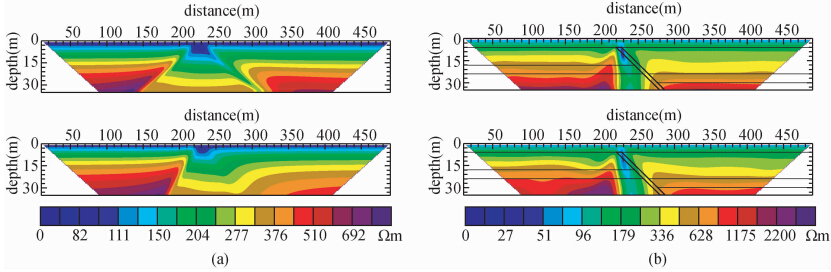 | 图 4 理论模型Ⅲ两种不同装置的正反结果图 (a)偶极—偶极装置;(b)三极装置. Fig. 4 Forward and inversion results with two different devices of model Ⅲ (a)Dipole-dipole device;(b)Three-pole device. |
2.3.3 表层为高阻层情况下的活动逆断层模型
图 5是表层为高阻层情况下的活动逆断层模型Ⅳ的偶极—偶极和三极两种装置的正反演模拟结果,可见视电阻率断面和反演电阻率断面均在断层处有明显显示,断层明显穿过覆盖层,仍是作为推断断层活动性的依据,基本可定性确定断层的性质,且仍可有效进行地质分层,但不能有效获取断层的倾角.同理,偶极—偶极装置的反演各层的电阻率精度仍高于三极装置的反演结果,且更有利于进行地质分层.
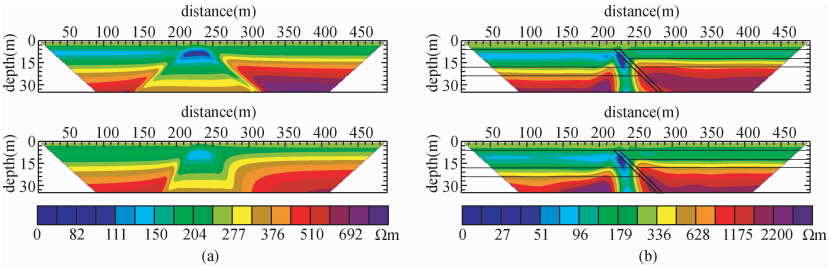 | 图 5 理论模型Ⅳ两种不同装置的正反结果图 (a)偶极—偶极装置;(b)三极装置. Fig. 5 Forward and inversion results with two different devices of model Ⅳ (a)Dipole-dipole device;(b)Three-pole device. |
3 实例应用与分析
针对实际常用的三种高密度电法装置(即温纳、温施和偶极—偶极),进行了现场数据采集,其主要采集参数:电极数为120个,电极距为6 m,最大隔离系数为32,供电电压为180 V.
高密度不同装置反演结果如图 6所示,纵观图 6反演结果可知,主要存在三条断层(F1、F2、F3),断层F1、F2和F3分别在测线100、175和205 m处有显示,这与钻孔资料相符合.对于F1断层,三种装置均有明显显示.对于F2、F3断层,偶极—偶极装置有明显显示,并可有效确定其倾向和倾角;温纳装置显示较明显,基本上可确定F2的倾向和倾角,但不易确定F3的性质;而温施装置显示不够明显,均不易确定其性质.实例应用说明高密度偶极—偶极装置对断层响应最为明显,温施装置次之,这与理论模拟结果完全相符.因此实际应用时宜采用偶极—偶极装置进行活动断层探测.
 | 图 6 实际资料三种不同装置的正反结果图 (a)温纳装置;(b)温施装置;(c)偶极—偶极装置. Fig. 6 Forward and inversion results with three different devices of actual data (a)Wenner device;(b)Wenner-schlumberger device;(c)Dipole-dipole device. |
4 结论与建议
4.1 基于断层是否穿过第四系判断断层活动的前提,理论模型模拟表明高密度各装置均可进行活动断层的定性探测和进行地质分层,基本上可定性确定断层的性质,但不能准确获取断层的倾角.
4.2 相对而言,高密度偶极—偶极装置进行活动断层的定性探测和地质分层是最有效的装置,三极装置次之.
4.3 表层为相对高阻层的地层结构有利于采用高密度电阻率进行地质分层,其精度高于表层为相对低阻层的地层结构.
4.4 通过理论模拟试验以及实例应用和分析可知,高密度偶极—偶极装置对活动断层的响应最敏感,可有效确定其性质,这与理论模拟结果完全相符.因此实际应用时宜采用偶极—偶极装置进行活动断层的探测.
致 谢 感谢审稿专家和编辑部老师的指导和帮助.
| [1] | Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method[J].Geophysics, 36(1): 132-155. |
| [2] | Constable S C, Parker R L, Constable C G. 1987.Occam'sinversion:A practical algorithm for egenerating smooth models from electromagnetic sounding data[J]. Geophysics,52(3): 289-300. |
| [3] | Chen Y L, Gan F P, Lu C J, et al. 2013. The study of underground river course detection by integrated geophysical methods in bare karst area[J]. Progress In Geophysics,28(3): 1608-1616. |
| [4] | Ding G Y, Tian Y J, Kong F C, et al. 1993. Active fault segmentation principles, methods and applications(in Chinese). Beijing: Seismological Press. |
| [5] | Fan C S, Li T L, Yan J Y. 2013. Research and application experiment on 2.5D SIP inversion[J]. Chinese J. Geophys. (in Chinese), 55(12): 4044-4050, doi:10.6038/j.issn.0001-5733.2012.12.016. |
| [6] | Li Z X, Zeng Z F, Li E Z, et al. 2005. The function of geophysical method in active fault detection and discuss of combining methods[J]. Journal of Jilin University(Earth Science Edition), 35(S1): 109-114. |
| [7] | Liu B, Li S C, Li S C, et al. 2010. 3D fem numerical forward modeling of direct current electrical resistivity based on pcg algorithm[J]. Chinese Journal of Geotechnical Engineering, 32(12): 1846-1852. |
| [8] | Liu B, Li S C, Li S C, et al. 2012. 3D electrical resistivity inversion with least-squares method based on inequality constraint and its computation efficiency optimization[J]. Chinese J. Geophys. (in Chinese), 55(1): 260-268,doi:10.6038/j.issn.0001-5733.2012.01.025. |
| [9] | Sasaki Y. 1989. Two-dimension joint inversion of magnetotelluric and dipole-dipole resistivity data[J].Geophysics,54(2): 254-262. |
| [10] | Sasaki Y. 1994. 3-D resistivity inversion using the finite-element method[J]. Geophysics, 59(12): 1839-1848. |
| [11] | Wan X L, Xi D Y, Gao E G, et al. 2005. 3-D resistivity inversion by the least-square QR factorization method under improved smoothness constraint condition[J]. Chinese J. Geophys. (in Chinese), 48(2): 439-444. |
| [12] | Wang Q J, Hu Y L, Dou X F, et al. 2009. Application of the high-density resistivity method in project exploration[J]. 24(1): 335-339. |
| [13] | Wu Z Q, Liu Y S, Liu B J, et al. 2005. Application of geophysical method to the precise positioning of urban seismic mobile moving fault[J]. Progress In Geophysics, 20(2): 528-533. |
| [14] | Wu Z Q, Yin C. 2007. Application of schlumberger transverse profiling method to detecting buried faults[J]. Chinese J. Geophys. (in Chinese), 50(2): 625-631. |
| [15] | Yi B, Zeng Z F, Li E Z, et al. 2005. The survey and research for alive fault in city by electrical prospecting[J]. Journal of Jilin University(Earth Science Edition), 35(S1): 115-118. |
| [16] | Yi B, Zeng Z F, Xue J, et al. 2008. Application of geophysical method in city active fault detection[J]. Progress In Geophysics, 23(2): 599-604. |
| [17] | 陈玉玲, 甘伏平, 卢呈杰, 等. 2013. 裸露岩溶区地下河管道综合地球物理方法探测研究[J]. 地球物理学进展, 28(3): 1608-1616. |
| [18] | 丁国瑜, 田勤俭, 孔凡臣, 等. 1993. 活断层分段-原则、方法及应用. 北京: 地震出版社. |
| [19] | 范翠松, 李桐林, 严加永. 2013. 2.5 维复电阻率反演及其应用试验[J]. 地球物理学报, 55(12): 4044-4050, doi:10.6038/j.issn.0001-5733.2012.12.016. |
| [20] | 李征西, 曾昭发, 李恩泽, 等. 2005. 地球物理方法探测活动断层效果和方法最佳组合分析[J]. 吉林大学学报: 地球科学版, 35(S1): 109-114. |
| [21] | 刘斌, 李术才, 李树忱, 等. 2010. 基于预条件共轭梯度法的直流电阻率三维有限元正演研究[J]. 岩土工程学报, 32(12): 1846-1852. |
| [22] | 刘斌, 李术才, 李树忱, 等. 2012. 基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J]. 地球物理学报, 55(1): 260-268,doi:10.6038/j.issn.0001-5733.2012.01.025. |
| [23] | 宛新林, 席道瑛, 高尔根, 等. 2005. 用改进的光滑约束最小二乘正交分解法实现电阻率三维反演[J]. 地球物理学报, 48(2): 439-444. |
| [24] | 王启军, 胡延林, 都兴锋, 等. 2009. 高密度电阻率法在工程勘查中的应用[J]. 地球物理学进展, 24(1): 335-339. |
| [25] | 吴子泉, 刘元生, 刘保金, 等. 2005. 地球物理方法在城市地震活动断层精确定位中的应用[J]. 地球物理学进展, 20(2): 528-533. |
| [26] | 吴子泉, 尹成. 2007. 电阻率横向剖面法及其在隐伏断层探测中的应用研究[J]. 地球物理学报, 50(2): 625-631. |
| [27] | 易兵, 曾昭发, 李恩泽, 等. 2005. 电法探测城市活断层的应用[J]. 吉林大学学报: 地球科学版, 35(S1): 115-118. |
| [28] | 易兵, 曾昭发, 薛建, 等. 2008. 地球物理方法对城市活断层的探测与研究[J]. 地球物理学进展, 23(2): 599-604. |
 2014, Vol. 29
2014, Vol. 29


