地球物理学进展  2014, Vol. 29 Issue (4): 1889-1894   PDF    
引用本文
陈载林, 范利飞, 王会波, 汪勇, 于秋莲. 磁总场梯度方法探测废弃炸弹[J]. 地球物理学进展, 2014, 29(4): 1889-1894, doi: 10.6038/pg20140455  
CHEN Zai-lin, FAN Li-fei, WANG Hui-bo, WANG Yong, YU Qiu-lian. Applying magnetic field gradient method to detect abandoned bombs. Progress in Geophysics, 2014, 29(4): 1889-1894, doi: 10.6038/pg20140455   
磁总场梯度方法探测废弃炸弹
陈载林1, 范利飞2, 王会波3, 汪勇4, 于秋莲1     
1. 云南国土资源职业学院, 昆明 650217;
2. 劳雷工业公司, 北京 100000;
3. 核工业航测遥感中心, 石家庄 050002;
4. 中国石油华北油田公司国际合作项目部, 任丘 062552
收稿日期: 2013-9-25 修回日期: 2013-12-21 .
基金项目：云南省地矿局科技创新基金（2012JJ03）和云南省教育厅科学研究基金（2013Y561）联合资助.
作者简介：陈载林，男，1983年生，云南昆明人，硕士研究生，讲师，主要从事地球物理教学及科研工作.（E-mail：327634884@qq.com）
摘要：为了探测二战时遗留的地下废弃炸弹，我们开展了磁总场梯度探测模拟实验.在此基础上探讨一些确定磁性体位置和范围的数据处理技术，如自适应化极、垂直二阶导数、三维解析信号及欧拉反褶积反演计算等.将这套数据采集的方法、数据处理的方法运用到实际的废弃炸弹探测中去，取得了一定的效果.研究表明：梯度磁测对于探测地表浅而小的磁性体效果较好、速度快，其数据采取自适应化极方法、垂直二阶导数的方法基本能够确定废弃炸弹的位置及个数，同时采用三维解析信号的数据处理方法能够确定废弃炸弹的方向，采用欧拉反褶积的方法能够确定废弃炸弹的埋藏深度.
关键词： 磁总场梯度     化极     二阶导数     欧拉反褶积     废弃炸弹    
Applying magnetic field gradient method to detect abandoned bombs
CHEN Zai-lin1, FAN Li-fei2, WANG Hui-bo3, WANG Yong4, YU Qiu-lian1    
1. Yunnan Land and Resources Vocational College, Kunming 650217, China;
2. Laurel Technologies, Beijing 100000, China;
3. Airborne Survey and Remote Sensing Center of Nuclear Industry, Shijiazhuang 050002, China;
4. International Cooperative Department, Petrochina Huabei Oilfield Company, Renqiu 062552, China
Abstract: In order to detect underground waste bomb left over from World War II, first of all, we have carried out a total magnetic field gradient detection simulation experiments, secondly, on this basis, explore some of the magnetic body to determine the location and extent of data processing techniques, such as adaptive reduction to the pole, vertical two order derivative, three-dimensional analytic signal and Euler deconvolution inversion calculation, etc, Then use this method of data collection, data processing method to the actual detection of abandoned bombs, and achieved certain results. We believe that the gradient magnetic measurement was a better, faster method for detecting superficial and small magnetic body. And used adaptive reduction to the pole, vertical two order derivative method is basically able to determine the location and number of abandoned bombs, while using three-dimensional analytic signal data processing method to determine the direction of abandoned bombs, using Euler deconvolution method to determine the depth of abandoned bombs.
Key words: magnetic field gradient     reduction to the pole     vertical two order derivative     Euler deconvolution     abandoned bombs    

0 引 言

磁法勘探是通过观测和分析由岩石、矿石(或其他探测对象)磁性差异所引起的磁异常，进而研究地质构造和矿产资源(或其他探测对象)的分布规律的一种地球物理勘探方法(丁鸿佳，1997；管志宁，2002；刘益中，2012).

而磁总场梯度测量是一种相对比较新的磁法测量方法(郭志宏，2004；李海侠， 2009，2010；郇恒飞，2012；骆遥，2012；冯彦，2103).该方法的特点是:

1)有更高的异常分辨力;

2)有“压深突浅”作用;

3)相当于加密测量，对异常定位更准确，采集的信息较总场测量更丰富;

4)基本不受日变和正常场等因素的影响;

5)测线布置不受构造走向的限制.

因此磁梯度测量日益受到重视.目前，从大量的资料收集来看，研究废弃炸弹的探测问题比较少，或者军事部门在做，但是由于保密原因未公开.本文在某军区开展磁总场梯度探测地下废弃炸弹的基础上，开展了大量梯度数据处理及转换工作，在此基础上，总结梯度磁异常规律，归纳梯度磁异常处理流程，探索梯度磁异常准确定位废弃炸弹的模式.

1 磁总场梯度测量原理

整个地球表面，都有地磁场的分布，而且磁场强度随时间与空间的不同而有所变化.但是我们研究的区域往往是比较小的，如果没有磁性物质的存在，地磁场可以看做不变，这个场就叫背景场.当其中有铁磁性物质存在时，由于受大地磁场的磁化作用，将会在其周围产生次生磁场，从而产生磁异常.因此，地下如果具有磁性特征的目标体，就可以通过观测其磁异常的变化，特别是垂直双探头数据的采集，来获磁总场T的梯度值，通过各种相关的数据处理就可以判定异常物的平面位置及埋深.

2 磁总场梯度常用处理方法

2.1 梯度计算

对上下两个探头磁场差值除以探头间距既可获得磁总场梯度数据.

2.2 网格化计算

对测网数据采用克里格插值方法进行网格化计算，就可以得到 ∂ΔT /∂z 磁总场梯度网格化数据(谢汝宽，2013).

2.3 磁总场梯度数据处理与转换 2.3.1 化极

磁异常ΔT作化极处理，即将磁异常转换为磁性怍处于地磁极位置的磁异常是一种常用数据处理方法.一般来说，磁化方向是难以知道的，化极时通常是假定磁化方向与地磁场方向一致，但是由于种种原因，化极结果往往出现畸变，本文采用一种自适应化极的方法(王纪恒，1993；骆遥，2013)来消除化极的畸变.

运用畸变规律，先以地磁场方向作为磁化方向化极，如果化极后负异常增大明显，正异常向南偏移，表明磁化倾角过大，应用相对较小的磁化倾角化极，反之则用较大的磁化倾角.该方法需要比较其化极异常图，既注意等值线形态的变化．也注意正负异常强度的变化，最终选择合理的化极结果.

2.3.2 垂直二阶导数

磁异常导数主要是突出浅源(局部)异常，特别是磁异常的高阶导数(孙鹏飞，2007；刘圣博，2011；马国庆，2011；张恒磊，2012；陈载林，2012)，具有更高的分辨力，能分辨旁侧选加异常和圈定磁性体的范围和位置.本文采用一种对化极数据求取垂直二阶导数的方法，能够更加准确的识别磁性体的位置及范围.

2.3.3 三维解析信号及欧拉反褶积反演计算

对 ∂ΔT /∂z 垂直梯度网格化数据采取欧拉反褶积计算，并在此基础上作适当改进，

解析信号法(既总梯度模法)和欧拉褶积(Nabighian， 1972，1974，1984；Roest，1992；刘长风，1994；范美宁，2008；鲁宝亮，2009；张季生，2011；骆遥，2011；王明，2012；王万银2012)反演方法是近十几年来发展较快的与磁场及梯度数据有关的两种主要反演解释方法.利用三维解析信号振幅的极大值直接圈定磁源边界(Roest，1992)，利用解析信号及其高阶导数的极大值估算磁性体的埋深(Shu-Kun Hsu，1996).该类方法最主要的功能在于通过解析信号振幅(即总梯度模)的极大值来确定磁源边界或中心水平位置，根据二维振幅曲线来估算磁源的埋藏深度.

其方法原理为：设i，j，k为X、Y、Z方向的单位矢量，则位场异常T的三维解析信号定义为

方程满足解析信号的基本要求.他们分别为希尔伯特变换对的实部和虚部.解析信号的振幅函数为

对网格化数据自动解释最有意义的是二维振幅函数.这是因为二度体上得磁异常解析信号振幅曲线的形状与磁化强度和地磁场方向无关.解析信号振幅的极大值对应于场源的位置.也就是说，可以根据解析信号振幅的极大值求得场源的水平位置.磁源的埋深可有解析信号振幅曲线求得.他们之间的关系为

式中，h为磁源的上顶埋深(若为水平圆柱体则表示中心埋深)，x1/2为振幅曲线的半极大值点的横坐标，α为校正系数.对于不同形体，其系数不同.

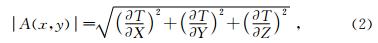
欧拉褶积反演方法是另一类快速估算场源中心位置的位场反演解释方法.该方法以欧拉齐次方程为基础，运用位场异常及其空间导数以及各种地质体具有的特定“构造指数”来确定异常场源的位置.

位场在场源之外满足拉普拉斯方程，一些特殊形状场源的位场为N阶齐次方程，N阶齐次方程也满足欧拉方程，欧拉方程的表达式为

式中，r 为场源点到观测点的距离向量，T是位场异常，N是方程的阶数.该方程的一个解为

在磁异常情况下，k为一常数，N可认为是异常幅值随距离增大的衰减度(异常衰减度).

Thompson于1982年首先推出了二维欧拉褶积反演方法，用于剖面磁测资料的解释.如果剖面位场函数ΔT(x，z)满足方程式

ΔT(t·x，t·z)=tN·ΔT(x，z)，

则称ΔT(x，z)是N阶齐次的，可以证明，如果函数ΔT(x，z)是N阶齐次的，则满足方程

此偏微分方程称作二维欧拉齐次方程，或简称二维欧拉方程.

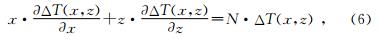
Reid等人1990年把二维欧拉褶积反演方法推广到三维情况，获得三维欧拉褶积反演方法.与二维情况类似，满足ΔT(t·x，t·y，t·z)=tN·ΔT(x，y，z)齐次关系的N阶齐次网格位场函数ΔT(x，y，z)同样满足下面的三维欧拉齐次方程：

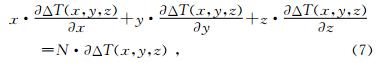
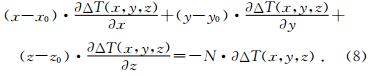
现在证明中心点位于(x0，y0，z0)的一些简单规则的磁性体(或重力密度体)满足下面欧拉方程：

并且其“构造指数”N与规则形体具有一定的对应关系.例如对磁场而言，球体、水平圆柱体、无限延深薄板、顺层磁化无限延深柱体(单电极)的“构造指数”N分别为1、1、2、3，见表 1，本文磁性体为废弃炸弹，故构造指数选取为1.

表 1 不同磁异常源的构造指数 Table 1 Stucture index of different magnetic anomaly sources

实际反演计算时，若考虑区域场或背景场B的影响，将位场异常视为区域场与点源场之和，则具体的欧拉方程变为

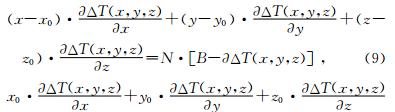
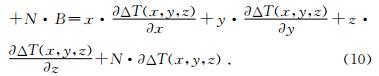
通过多个网格数据点上的磁场或者重力场及梯度数据，解欧拉方程式组成的超定方程的最小二乘意义解，可反演得到场源位置及深度既(x0，y0，z0).所以公式(10)就是我们最终用于进行平面网格位场数据反演计算磁源位置的欧拉反褶积方程式.

3 垂直磁梯度在废弃炸弹探测中的应用

3.1 已知炸弹区的实验

为了了解垂直磁梯度测法探测废弃炸弹及数据处理的有效性，军方划定了一块东西向宽14 m，南北向长18 m的区域，事先在某位置埋藏了炸弹，供实验之用.

我们采用G-858SX高精度铯光泵磁力仪开展了垂直磁梯度测量工作，线距1 m，快速连续测量，让后对采集的数据进行了上述处理，获得了以下成果.

表 2 实验区磁性体预测成果表 Table 2 The experimentation area magnetic body prediction table

从图 1a梯度磁异常图件中只能看出异常的位置，只能推测炸弹的可能位置，但是在开展了自适应手工化极(采用参数D=-4.9，I=5)及垂直二阶导数运算后，可以得到磁性体的相对准确位置，但是深度问题不能确定，在开展了三维解析信号及欧拉反褶积运算后，可以得到磁性体的位置，与图 1b及图 1c基本吻合，及磁性体的深度为1.4 m.

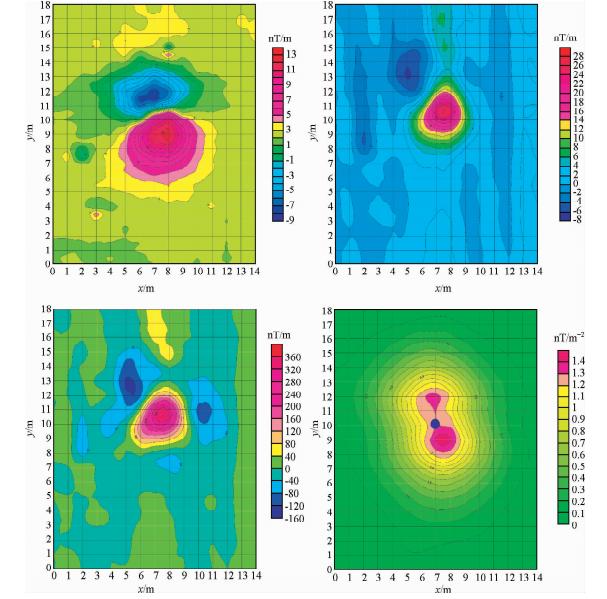图 1 实验区磁总场梯度及数据处理与转换平面等值线图 Fig. 1 The experimentation area magnetic field gradient and data processing and conversion contour map

后期我们将预测位置(X=7，Y=10)及深度(1.4 m)报告于军方，与军方反馈于磁性体位置(X=7，Y=10)及深度(1.5 m)比较吻合，得到了较好的处理效果，为我们在废弃炸弹区开展进一步工作提供了技术支持.

3.2 废弃炸弹区的探测

废弃炸弹区位于军方某空地，为二战时遗留的废弃炸弹，由于时代久远，炸弹性质不明，炸弹准确位置不明，一直不敢开挖，为此，我们在前述开展理论研究、模拟实验的基础上，在此区域大胆开展梯度磁测工作、数据处理、分析解释工作，得到了以下成果.

通过梯度磁法测量，图 2a异常相对较小，负异常不明显，推测废弃炸弹由于时代久远，磁性减弱，磁化方向可能已经为被地磁场磁化，故化极处理可以考虑有当地地磁方向(D=-4.9，I=45)化极，处理后，效果明显，异常位置1为(X=7.5，Y=8.5)，异常位置2为(X=9.5，Y=10.5)，推测可能有两个磁性体，垂直二阶导数处理后效果更加明显，见图 2c，同样在三维解析信号及欧拉反褶积运算后，可以反映磁性体的位置，最后预测地下有两个废弃炸弹，位置在(X=6-10，Y=7-12)之间，埋藏深度在1.5 m左右.

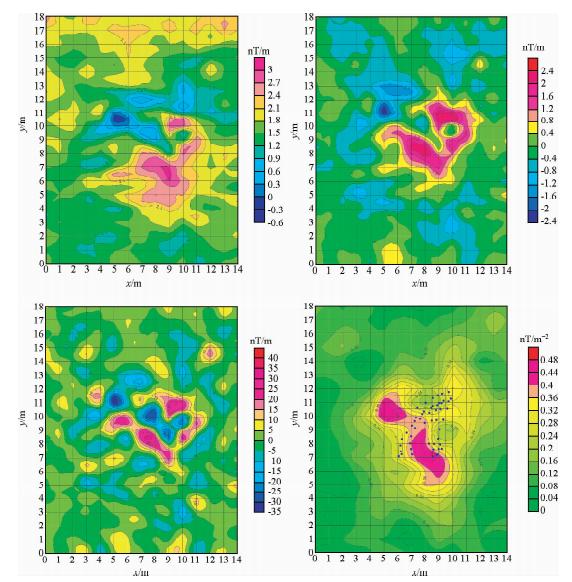图 2 未知炸弹区磁总场梯度及数据处理与转换平面等值线图 Fig. 2 The Unknown bomb zone magnetic field gradient and data processing and conversion contour map
4 结 论

4.1     梯度磁测具有较多的优点，特别是对于探测地表浅而小的磁性体效果较好、速度快，使得梯度磁测在军事领域中对于废弃炸弹的探测有一定的运用价值.

4.2      本文对梯度磁测数据采取自适应化极方法、垂直二阶导数的方法基本能够确定废弃炸弹的位置及个数，同时采用三维解析信号的数据处理方法能够确定废弃炸弹的方向，采用欧拉反褶积的方法能够确定废弃炸弹的埋藏深度.

致 谢 感谢外审专家和编辑老师对本文的帮助.

参考文献
[1] Ban L. 2009. 3-D Gravity and Magnetic Inversion for Physical Properties Based on the Correlation Constraint (in Chinese)[D][Ph. D. thesis]. Beijing: China University of Petroleum.
[2] Chen Z L, Zuo Q H, Wang J F. 2013. Magnetic prospecting on magnetmining exploration area of Laos bokeo province[J].   Progress in Geophysics (in Chinese), 28(3): 1447-1452.
[3] Ding H J, Liu S J. 1997. Progress in the study of weak magnetic measurement in china. Chinese J. Geophys. (in Chinese), 40(S1): 238-248.
[4] Fan M L, Jiang Y B, Zhang J X. 2008. Model calculation of euler's equation for different data types[J]. Progress in Geophysics (in Chinese), 23(4): 1250-1253.
[5] Feng Y, Jiang Y, Sun H, et al. 2013. Calculation and analysis of geomagnetic field horizontal gradients and high altitude geomagnetic field[J]. Progress in Geophysics (in Chinese), 28(2): 735-746.
[6] Guan Z N, Hao T Y, Yao C L. 2002. Prospect of gravity and magnetic exploration in the 21st century[J]. Chinese J. Geophys. (in Chinese), 17(2): 237-244.
[7] Guo Z H. 2004. The practical improvement of forward and inversion Technique on aeromagnetic gradient data and its application (in Chinese) [D]. Beijing: China University of Geosciences.
[8] Huan H F, Wu Y G, Guan Y W, et al. 2012. Deep structure inversion by measurement of vertical gradient of gravity for a profile of Changbai mountain area[J]. Global Geology (in Chinese), 31(4): 791-796.
[9] Li H X. 2009. Study of continuation and transformation methods for aeromagnetic gradient anomalies (in Chinese) [D][Ph. D. thesis]. Zhejiang: Zhejiang University.
[10] Li H X, Xu S Z, Yu H L, et al. 2010. Transformations of aeromagnetic total field and gradient components in the frequency domain[J]. Progress in Geophysics (in Chinese), 25(4): 1396-1405.
[11] Liu C F, Liu H J. 1994. Inversion of magnetic anomaly data in Taiwan strait using Euler deconvolution[J]. Chinese J. Geophys.   (in Chinese), 37(3): 345-352.
[12] Liu S B, Chen C, Hu Z W. 2011. The application and characteristic of vertical first-order derivative of the total magnitude magnetic anomaly[J]. Progress in Geophysics (in Chinese), 26(2): 647-653.
[13] Liu Y Z, Li C L, Zhou X M, et al. 2012. Application of regional aeromagnetic data in predicting the northern regional geothermal field in Songliao Basin[J]. Chinese J. Geophys. (in Chinese), 55(3): 1063-1069.
[14] Lu B L, Fan M N, Zhang Y Q. 2009. The calculation and optimization of structure index in Euler deconvolution[J]. Progress in Geophysics (in Chinese), 24(3): 1027-1031.
[15] Luo Y. 2013. Hartley transform for reduction to the pole[J]. Chinese Journal Geophysics (in Chinese), 56(9): 3163-3172.
[16] Luo Y, Wang M, Luo F, et al. 2011. Direct analytic signal interpretation of potential field data using 2-D Hilbert transform[J]. Chinese J. Geophys. (in Chinese), 54(7): 1912-1920.
[17] Luo Y, Wang P, Duan SL, et al. 2012. Leveling total field aeromagnetic data with measured vertical gradient[J]. Chinese J. Geophys. (in Chinese), 55(11): 3854-3861.
[18] Ma G Q, Du X J, Li L L, et al. 2011. Utilizing total horizontal derivate of tilt angle and Euler deconvolution to study the linear structure of the Sichuan Basin[J]. Progress in Geophysics (in Chinese), 26(3): 916-921.
[19] Nabighian M N. 1972. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section its properties and use for automated anomaly interpretation[J].   Geophysics, 37(2): 507-512.
[20] Nabighian M N. 1974. Additional comments on the analytic signal of two-dimensional magnetic bodies with polygonal crosssection[J].   Geophysics, 39(1): 85-92.
[21] Nabighian M N. 1984. Toward a three dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations[J].   Geophysics, 49(6): 780-786.
[22] Roest W R, Verhoef J, Pilkington M. 1992. Magnetic interpretation using 3-D analytic signal[J].   Geophysics, 57(1): 116-125.
[23] Shi L, Guo L H, Meng X H. 2012. 3D correlation imaging of the vertical gradient of magnetic total field anomaly[J]. Progress in Geophysics (in Chinese), 27(4): 1609-1614.
[24] Shu-Kun H, Sibuet J C, Shyu C T. 1996. High-resolution detection of geologic boundaries from potential-field anomalies: An enhanced analytic signal technique[J].   Geophysics, 61(2): 373-386.
[25] Sun P F, Wu Y G. 2007. Make use of vertical and horizontal differential coefficient of the gravitation and magnetic force to ensure the grads of the northeast china[J]. Journal of Jilin University (Earth Science Edition), 37(S1): 27-31.
[26] Thompson D T. 1982. EULDPH-A new technique for making computer assisted depth estimates from magnetic data[J].   Geophysics, 47(1): 31-37.
[27] Wang J H. 1993. Some understanding for reduction to the pole of magnetic anomaly[J]. Computer Techniques for Geophysical and Geochemical Exploration (in Chinese),15(4): 333-338.
[28] Wang M, Luo Y, Luo F, et al. 2012. The application and development of Euler deconvolution in gravity and magnetic field [J]. Geophysical and Geochemical Exploration (in Chinese), 36(5): 834-841.
[29] Wang W Y. 2012. Spatial variation law of the extreme value position of analytical signal amplitude for potential field data[J]. Chinese J. Geophys. (in Chinese), 55(4): 1288-1299.
[30] Xie R K, Wang P, Guo H, et al. 2013. Aeromagnetic total field gridding enhancement with horizontal gradient[J]. Chinese Journal Geophysics (in Chinese), 56(2): 660-666.
[31] Zhang H L, Hu X Y, Liu T Y. 2012. Fast inversion of magnetic source boundary and top depth via second order derivative[J]. Chinese J. Geophys. (in Chinese), 55(11): 3839-3847.
[32] Zhang J S, Gao R, Li Q S, et al. 2011. A combined Euler and analytic signal method for an inversion calculation of potential data[J]. Chinese J. Geophys. (in Chinese), 54(6): 1634-1641.
[33] 班丽. 2009. 相关约束重磁三维定量反演方法研究[D][博士论文].   北京: 中国石油大学.
[34] 陈载林, 左琼华, 王建飞. 2013. 老挝波乔省某磁铁矿区磁法勘探[J].   地球物理学进展, 28(3): 1447-1452.
[35] 丁鸿佳, 刘士杰. 1997. 我国弱磁测量研究的进展[J].   地球物理报, 40(S1): 238-248.
[36] 范美宁, 江裕标, 张景仙. 2008. 不同数据用于欧拉方程的模型计算[J].   地球物理学进展, 23(4): 1250-1253.
[37] 冯彦, 蒋勇, 孙涵,等. 2013. 地磁场水平梯度及高空地磁场的计算与分析[J].   地球物理学进展, 28(2): 735-746.
[38] 管志宁, 郝天珧, 姚长利. 2002. 21世纪重力与磁法勘探的展望[J].   地球物理学进展, 17(2): 237-244.
[39] 郭志宏. 2004. 航磁及梯度数据正反演解释方法技术实用化改进及应用[D][博士论文].   北京: 中国地质大学.
[40] 郇恒飞, 吴燕冈, 管彦武,等. 2012. 利用实测重力垂直梯度反演长白山地区一剖面的深部构造[J].   现代地质, 31(4): 791-796.
[41] 李海侠. 2009. 航磁梯度异常的延拓与转换方法研究[D][博士论文].   浙江: 浙江大学.
[42] 李海侠, 徐世浙, 余海龙,等. 2010. 频率域航磁总场与梯度分量的转换研究[J].   地球物理学进展, 25(4): 1396-1405.
[43] 刘长风, 刘慧洁. 1994. 用Euler反褶积方法反演台湾海峡磁异常[J].   地球物理学报, 37(3): 345-352.
[44] 刘圣博, 陈超, 胡正旺. 2011. 磁异常模量垂向一阶导数的特征及应用[J].   地球物理学进展, 26(2): 647-653.
[45] 刘益中, 李成立, 周锡明,等. 2012. 区域航磁资料在预测松辽盆地北部区域地温场中的应用.   地球物理学报, 55(3): 1063-1069.
[46] 鲁宝亮, 范美宁, 张原庆. 2009. 欧拉反褶积中构造指数的计算与优化选取[J].   地球物理学进展, 24(3): 1027-1031.
[47] 骆遥. 2013. Hartle变换化极[J]. 地球物理学报, 56(9): 3163-3172
[48] 骆遥, 王明, 罗锋,等. 2011. 重磁场二维希尔伯特变换——直接解析信号解释方法[J].   地球物理学报, 2011, 54(7): 1912-1920.
[49] 骆遥, 王平, 段树岭,等. 2012. 航磁垂直梯度调整ΔT水平方法研究[J].   地球物理学报, 55(11): 3854-3861.
[50] 马国庆, 杜晓娟, 李丽丽,等. 2011. 利用倾斜角总水平导数和欧拉反褶积法研究四川盆地线性构造[J].   地球物理学进展, 26(3): 916-921.
[51] 石磊, 郭良辉, 孟小红. 2012. 磁总场异常垂直梯度三维相关成像[J].   地球物理学进展, 27(4): 1609-1614.
[52] 孙鹏飞, 吴燕冈. 2007. 利用重磁水平和垂直二阶导数确定东北地区梯度带[J].   吉林大学学报(地球科学版), 37(S1): 27-31.
[53] 王纪恒. 1993. 关于磁异常化极的若干体会[J].   物化探计算技术, 15(4): 333-338.
[54] 王明, 骆遥, 罗锋,等. 2012. 欧拉反褶积在重磁位场中应用与发展[J].   物探与化探, 36(5): 834-841.
[55] 王万银. 2012. 位场解析信号振幅极值位置空间变化规律研究[J].   地球物理学报, 55(4): 1288-1299.
[56] 谢汝宽, 王平, 郭华,等. 2013. 考虑航磁水平梯度变化的ΔT网格化方法研究[J].   地球物理学报, 56(2): 660-666.
[57] 张恒磊, 胡祥云, 刘天佑. 2012. 基于二阶导数的磁源边界与顶部深度快速反演[J].   地球物理学报, 55(11): 3839-3847.
[58] 张季生, 高锐, 李秋生,等. 2011. 欧拉反褶积与解析信号相结合的位场反演方法.   地球物理学报, 54(6): 1634-1641.