地球物理学进展  2014, Vol. 29 Issue (4): 1798-1802   PDF    
引用本文
王彦仓, 杜维良, 刘喜恒, 秦凤启, 佟凤芝. 利用测井数据实现横波速度的反演及应用效果分析[J]. 地球物理学进展, 2014, 29(4): 1798-1802, doi: 10.6038/pg20140441  
WANG Yan-cang, DU Wei-liang, LIU Xi-heng, QIN Feng-qi, TONG Feng-zhi. Inversion of transverse wave velocity with logging data and its effect analysis of application. Progress in Geophysics, 2014, 29(4): 1798-1802, doi: 10.6038/pg20140441   
利用测井数据实现横波速度的反演及应用效果分析
王彦仓, 杜维良, 刘喜恒, 秦凤启, 佟凤芝    
华北油田公司 地球物理勘探研究院, 任丘 066552
收稿日期: 2013-11-11 修回日期: 2014-3-3 .
作者简介：王彦仓，男，1963生，高级工程师，2001年在中国石油大学硕士学位，现在中国石油华北油田公司地球物理勘探研究院工作，长期从事石油地球物理勘探、煤层气综合研究及管理工作.（E-mail：wty_wyc@petrochina.com.cn）
摘要：在地震数据的AVO（Amplitude Versus Offset）反演以及储层预测分析等中都需要横波速度信息，然而目前多数地区横波速度测井资料十分匮乏，在AVO反演中，往往凭经验公式获得，其精度很低. 为了获得准确的横波速度信息，我们利用测井资料由最小二乘法实现横波速度的反演，针对华北油区赛83井实际测井数据，利用纵波速度、密度测井数据反演计算了该区的横波速度，并与实测横波速度作了对比，结果发现反演与实测结果取得了较好的一致性；还将该方法反演的横波速度与几种不同反演方法反演结果作了对比，获得较为一致的结果，算例证明了该方法的有效性.在测井资料缺少的情况下，该方法作为AVO反演横波速度的初始速度建模及储层预测分析应该是一种较为实用的方法.
关键词： 横波速度的反演     测井数据     AVO反演    
Inversion of transverse wave velocity with logging data and its effect analysis of application
WANG Yan-cang, DU Wei-liang, LIU Xi-heng, QIN Feng-qi, TONG Feng-zhi    
Institute of Geophysical Exploration of North China Oilfield, Renqiu 066552, China
Abstract: It is well known that the information of transverse wave velocity is needful in the AVO (Amplitude Versus Offset)inversion and the reservoir forecasting, however, the logging data of transverse wave velocity is very lacking. In the AVO (Amplitude Versus Offset) inversion, the conventional method of transverse wave velocity gotten by experiential formulae, its precision is very poor. In order to get the velocity of transverse wave we have realized the inversion transverse wave velocity with the logging data, and applied it to compute the transverse wave velocity in the SAI 83 well region. The inversion results are in agreement with the experiential results. We have also given the computational compare in the application of AVO inversion. The results show that by this method gotten the transverse wave velocity applied as the initial value of AVO inversion the inversion precision has been clearly improved, proved the validity of this method.
Key words: inversion of transverse wave velocity     logging data     AVO inversion    
0 引 言

叠前多参数反演所需要的一个重要参数是利用井点横波速度参数作为约束，但横波测井资料非常缺乏，缺少横波速度参数作为约束的反演，其计算结果难以标定和评估.由于目前测井资料丰富，测井种类多，精度相对高，因此利用测井曲线来反演横波速度是目前地球物理工作者研究的热点问题(Gassmann，1951; Eshelby，1957; Han et al., 1986; Batzle and Wang， 1992; Xu and White， 1995，1996; Keys and Xu， 2002; White and Castagna， 2002; 白俊雨等，2012; 巴晶等，2013).Gassmann(1951)对岩石孔隙以及含流体性质对地震性质影响进行了深入研究，建立了 Gassmann方程，尽管方程的建立有多条假设，但有许多参数是可以通过测井资料得到的，因此是目前最普遍采用的方法，近年有较多的应用与研究报道(Toksöz et al., 1976; Fred，2006; 刘福平等，2008a;白俊雨等，2012;张广智等，2013).然而Gassmann方程的其应用条件是苛刻的，需要多种测井资料，在大量的油区仍然难以满足和获取这些资料，尽量利用较少的测井资料又能获得较为准确的横波资料这是解决实际问题所期盼的(Toksöz et al., 1976; 李景叶等，2005; Fred，2006; Fred，2006;刘福平等，2008; 白俊雨等，2012;张广智等，2013)，在华北油田赛83井区，由于储层纵波速度与围岩速度重叠比较明显，因此利用地震资料叠后反演进行储层研究受到了极大地制约，在所采集到的15口井的测井资料中只有赛83井有横波测井资料，并且大部井的测井资料也不全，无法利用Gassmann方程反演这些井横波资料，为了对该区进行精确的叠前地震反演，需对常规测井资料进行横波研究的工作，从而为该区进行进一步地勘探和开发服务，我们利用测井资料由最小二乘法实现横波速度的反演，针对华北油区赛83井实际测井数据，利用纵波速度、密度测井数据由最小二乘法实现该区的横波速度反演，反演与实测结果取得了较好的一致性，还将该方法反演的横波速度与几种不同反演方法反演结果作了对比，获得较为一致的结果，算例证明了该方法的有效性.在测井资料缺少的情况下，该方法作为AVO反演横波速度的初始速度建模及储层预测分析应该是一种较为实用的方法. 1 横波速度反演算法

弹性介质中等效纵、横波速度可写为(杨锴和马在田，2006; 陆基孟，1993)

其中λ、μ、ρ分别为介质的拉梅(Lame)系数和地层介质密度.

反演的重要基本方法之一是基于导数的反演方法(陆基孟，1993; 李景叶等，2005; Shou et al., 2006; 吴庆举等，2006; 刘福平等，2007)，以合成测井记录和实际测井记录之差建立基于岩石物理模型方程的反演目标函数.将目标函数对地层纵、横波速度等参数求导使目标函数最小化，建立反演地层纵、横波速度反演方程.

取纵波速度理论计算结果Vp与测量结果Vp，ob的绝对误差函数为

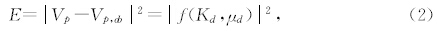
其中，f=Vp－Vp，ob，Vp由方程(1)计算.取最小二乘法解得如下迭代计算公式

其中 A k=[ ∇ f]，x =[λ，μ]T，k为解 x k的第k次近似， b= ∇ fk x k-fk= A k x k-fk ，利用方程(3)、(4)通过反复迭代可实现拉梅(Lame)系数λ、μ的计算，再利用(1)式可实现地震波速度的反演.在这一反演方法的迭代过程中需要偏导矩阵 A(称Jacobi矩阵)的反复计算.

由(1)式的前式分别对λ、μ求导数得

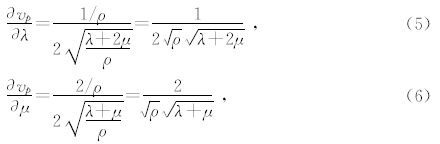
再利用公式(5)~(6)可实现偏导矩阵 A 的计算，从而实现横波速度的反演. 2 实际算例与分析 2.1 实际资料的横波速度与计算结果

本研究将以赛83井的横波速度计算为例，说明所提出的利用测井资料反演横波速度易行算法的可行性，并利用实测横波速度测量结果分析反演数据的反演精度.这口井有：井径、横波速度、纵波速度、密度测井数据，下面利用纵波速度、密度测井数据反演地震波的横波速度，实测横波速度用于对比反演结果的精度分析.

在这里只利用纵波速度、介质密度测井资料反演地层横波速度，由于测井曲线中没有直接给出固体矿物弹性模量等的测量结果，因测井资料的缺少，计算横波速度的方法就无法使用Biot-Gassmann等模型实现地层有效弹性参数的计算，在此只用纵波速度、介质密度测井资料由公式(3)和(4)可实现反演横波速度的计算.

图 1~图 3 显示了赛83井的横波反演结果.图中： CAL 井径；VS为实测横波速度；VS-ZD为速度估计的横波速度；VP为实测纵波速度；DEN为密度；GR为自然γ，反演井段为：1840～2150 m，实测的横波曲线井段也为：1840～2150 m井段.在图 1~图 3中，曲线名为VS的黑实线是实测的横波曲线，曲线名为VS-g红实线是估算的横波曲线.

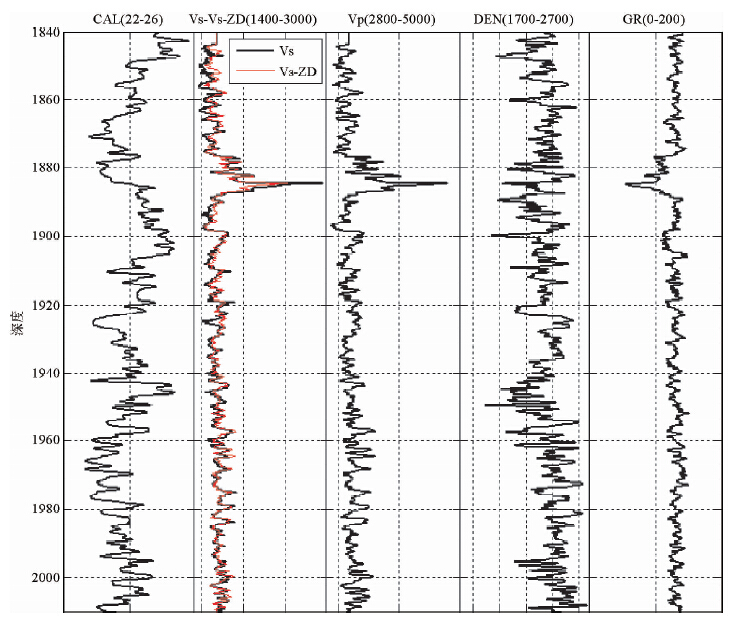图 1 赛83井用纵波和密度估算横波速度结果图(1840～2010 m) Fig. 1 The computing results of transverse wave velocity with the compression wave and density logging data of Sai 83 Well(1840～2010 m)

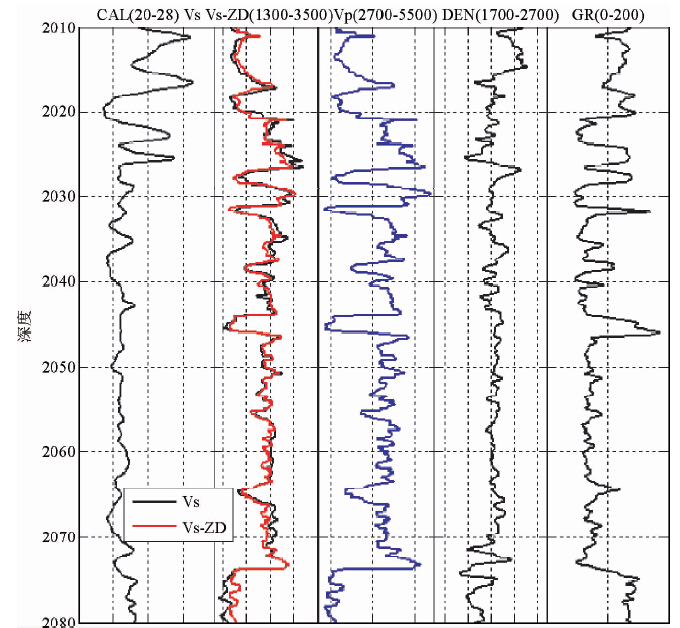图 2 赛83井用纵波和密度估算横波速度结果图(2010～2080 m) Fig. 2 The computing results of transverse wave velocity with the compression wave and density logging data of Sai 83 Well(2010～2080 m)

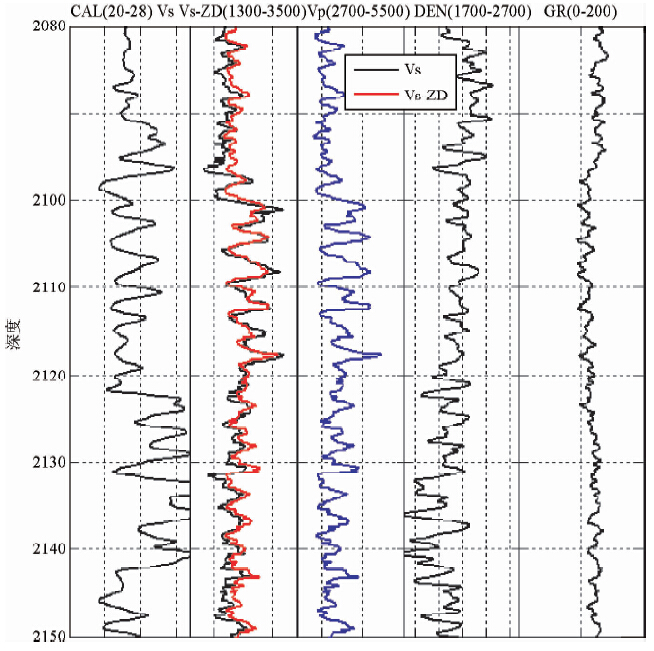图 3 赛83井用纵波和介质密度估算横波速度结果图(2080～2150 m) Fig. 3 The computing results of transverse wave velocity with the compression wave and density logging data of Sai 83 Well(2080～2150 m)

从计算结果可以看出，在横波测井曲线幅值抖动比较大的区段，曲线的幅值变化剧烈，特别是实测横波曲线峰值点处，计算结果与测量结果存在较大的误差，有的计算结果大于实测结果，但也有的计算结果小于实测结果，在实测横波曲线幅值抖动较小的区段，计算结果与测量结果存在误差较小，有些区段的计算结果大于实测结果，也有计算结果小于实测结果的，但两者大多数误差一般小于5%，从这一结果比较看出：估计的横波曲线与实测的横波曲线吻合是较好的.

在整个井段，估计的横波曲线与实测横波曲线可比性非常好，变化的趋势是完全一致的，曲线的相似性非常好，没有出现曲线凹凸反转现象，大量井段的相对误差一般不超过5%.

在井径明显变化的深度段估算结果没有明显的标志，反演与实测的横波值误差没有明显变化.

为说明该方法的反演效果用3了种不同的反演方法进行了计算，图 4为三种不同反演方法估算的横波速度图，其中VS为实测横波速度； VS-Z为纵波直接估算横波速度； VS-ZD为用纵波和密度估算的横波速度； VS-G为用Gassmann方程估计的横波速度； VP为实测纵波速度.对这三种方法作了分析比较，通过统计:大部分误差在5%以内，三种方法估算的横波速度和实测横波速度曲线形态相似、吻合较好(用该反演方法也可实现VS-Z反演曲线的计算)，三者与实测的误差都较小，Gassman方法估算的曲线更接近实测值.但当在缺乏测井资料的情况下该方法也不失为一种好的选择.

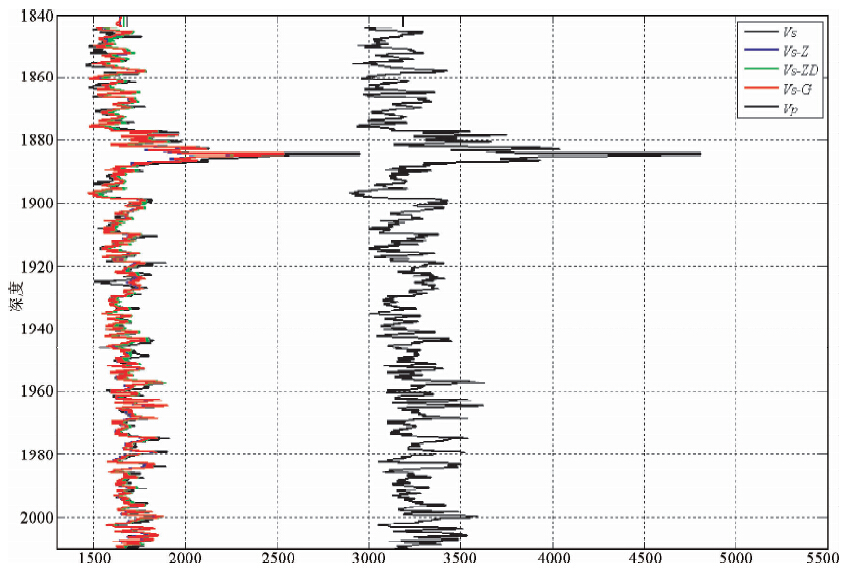图 4 赛83井横波速度反演结果对比图(1840～2000 m) Fig. 4 The comparisons of transverse wave velocity computed of Sai 83 Well(1840～2000 m)
3 结 论

叠前多参数反演所需要的一个重要参数是利用井点横波速度参数作为约束，但横波测井资料非常缺乏，缺少横波速度参数作为约束的反演，其计算结果难以标定和评估.目前所使用的Biot-Gassmann等模型实现横波速度反演是需要多种测井数据的，这些方法也无法满足实际需要，为此本文提出的只用纵波速度、 介质密度实现反演横波速度方法.

利用华北油区赛83井实际测井数据，实现了横波速度反演计算，并与实测横波速度进行了对比分析，与实测结果取得了很好的一致，证明了算法有效性.该方法作为在测井资料缺少的条件下实现AVO反演的横波速度初始建模及储层预测分析应该是一种较为实用的方法.

参考文献
[1] Ba J, Yang X F, Chen Z Y, et al. 2013. rock physics model and gas saturation inversion for heterogeneous gas reservoirs[J]. Chinese J. Geophys. (in Chinese), 56(5): 1696-1706.
[2] Bai J Y, Song Z X, Su L, et al. 2012. Error analysis of shear-velocity prediction by Xu-White model[J]. Chinese J. Geophys. (in Chinese), 55(2): 589-595.
[3] Li J Y, Chen X H, Hao Z J, et al. 2005. A study on multiple time-lapse seismic AVO inversion[J]. Chinese J. Geophys(in Chinese), 48(4): 902-908.
[4] Liu F P, Zhang H M, Yang C C, et al. 2007. The quasi total reflected lateral shift of inhomogeneous p-polarized electromagnetic wave on the interface of conductive media [J]. Chinese J. Geophys. (in Chinese), 50(2): 556-566.
[5] Liu F P, Gao J, Li R Z, et al. 2008b. The influence on normal moveout of total reflected SV-wave by Goos-Hanchen effect at a free surface of stratum[J]. Chinese J. Geophys.(in Chinese), 51(3): 862-868.
[6] Fred J H. 2006. Seismic Amplitude Interpretation (in Chinese) [M]. Sun X P, Zhao L W, (translation). Dongying: Petroleum Industry Press, 18-39.
[7] Lu J M. 1993. Seismic Exploration Principle (2nd ed., in Chinese)[M]. Dongying: Petroleum of University Press, 123-194.
[8] Wu Q J, Li Y H, Zhang R Q, et al. 2006. 2D Kirchhoff Migration for Receiver Function [J]. Chinese J. Geophys. (in Chinese), 50(2): 539-545.
[9] Yang K, Ma Z T. 2006. Common reflection surface stack by an output imaging scheme[J]. Chinese J. Geophys. (in Chinese), 49(2): 546-553.
[10] Zhang G Z, Chen H Z, Wang Q, et al. 2013. Estimation of S-wave velocity and anisotropic parameters using fractured carbonate rock physics model[J]. Chinese J. Geophys. (in Chinese), 56(5): 1707-1715.
[11] Batzle M, Wang Z. 1992. Seismic properties of pore fluids[J]. Geophysics, 57(11): 1396-1408.
[12] Berryman J G. 1992. Single-scattering approximations for coefficients in Boit's equations of poroelasticities[J]. J. Acoust. Soc. Am., 91(2): 551-571.
[13] Eshelby J D. 1957. The determination of the elastic field of an ellipsoidal inclusion and related problems[J]. Proce. Roy. Soc. A, 241(1226): 376-396.
[14] Gassmann F. 1951. Elasticity of porous rock. Vierteljahrschrift der Naturorschenden Gescllschaft in urich, 96: 1-21.
[15] Han D H, Nur A, Morgan D. 1986. Effects of porosity and clay content on wave velocities in sandstones[J]. Geophysics, 51(11): 2093-2107.
[16] Keys R G, Xu S Y. 2002. An approximation for the Xu-White velocity model[J]. Geophysics, 67(5): 1406-1414.
[17] Kuster G T, Toksöz M N. 1974. Velocity and attenuation of seismic waves in two phase media: Part I: Theoretical formulation[J]. Geophysics, 39(5): 587-606.
[18] Mavko G, Mukerji T, Dovrkin J. 1996. The Rock Physics Handbook[M]. Standford: Standford Rock Physics Laboratory.
[19] Shou H, Liu H, Gao J H. 2006. AVO inversion based on common shot migration[J]. Applied Geophysics, 3(2): 99-104.
[20] Toksöz M N, Cheng C H, Timur A. 1976. Velocities of seismic waves in porous rocks[J]. Geophysics, 41(4): 621-645.
[21] White L, Castagna J. 2002. Stochastic fluid modulus inversion[J]. Geophysics, 67(6): 1853-1843.
[22] Xu S Y, White R E. 1995. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 43(1): 91-118.
[23] Xu S, White R E. 1996. A physical model for shear-wave velocity prediction[J]. Geophysical Prospecting, 44(4): 687-717.
[24] 巴晶, 晏信飞, 陈志勇,等. 2013. 非均质天然气藏的岩石物理模型及含气饱和度反演[J]. 地球物理学报, 56(5): 1696-1706.
[25] 白俊雨, 宋志翔, 苏凌,等. 2012. 基于Xu White 模型横波速度预测的误差分析[J]. 地球物理学报, 55(2): 589-595.
[26] 李景叶, 陈小宏, 郝振江,等. 2005. 多波时移地震AVO反演研究[J]. 地球物理学报, 48(4): 902-908.
[27] 刘福平, 李瑞忠, 杨长春,等. 2007. 非均匀P—偏振电磁波在导电界面的类全反射横向偏移[J]. 地球物理学报, 50(2): 556-566.
[28] 刘福平, 高杰, 李瑞忠,等. 2008. Goos-Hnchen效应对自由表面全反射SV波校正时差的影响[J]. 地球物理学报, 51(3): 862-868.
[29] Fred J H著. 2006. 地震振幅解释[M]. 孙夕平, 赵良武译, 北京: 石油工业出版社, 18-39.
[30] 陆基孟. 1993. 地震勘探原理(上, 下)[M]. 东营: 石油大学出版社, 123-194.
[31] 吴庆举, 李永华, 张瑞青,等. 2006. 接受函数的可希霍夫2D偏移方法[J]. 地球物理学报, 50(2): 539-545.
[32] 杨锴, 马在田. 2006. 输出道成像方式的共反射面元叠加方法Ⅱ----理论[J]. 地球物理学报, 49(2): 546-553.
[33] 张广智, 陈怀震, 王琪,等. 2013. 基于碳酸盐岩裂缝岩石物理模型的横波速度和各向异性参数预测[J]. 地球物理学报, 56(5): 1707-1715.