地球物理学进展  2014, Vol. 29 Issue (4): 1766-1771   PDF    
引用本文
王帅, 张永志, 姜永涛, 刘宁. 维多样性的动态权重粒子群算法反演断层滑动速率[J]. 地球物理学进展, 2014, 29(4): 1766-1771, doi: 10.6038/pg20140437  
WANG Shuai, ZHANG Yong-zhi, JIANG Yong-tao, LIU Ning. Slip velocity of fault induced by PSO algorithm with dynamical inertial weight and dimension mutation. Progress in Geophysics, 2014, 29(4): 1766-1771, doi: 10.6038/pg20140437   
维多样性的动态权重粒子群算法反演断层滑动速率
王帅, 张永志, 姜永涛, 刘宁    
长安大学地质工程与测绘学院, 西安 710054
收稿日期: 2013-11-11 修回日期: 2013-12-31 .
基金项目：国家自然科学基金项目（41374028，40674001）、国土资源大调查项目（1212010914015）和中央高校基本科研业务费专项资金（CHD2012TD004）联合资助.
作者简介：王帅，男，1988年生，河南新乡人，长安大学在读硕士研究生，研究方向：地壳形变与地球动力学.（E-mail：wang0814082shuai@163.com）
摘要：把维多样性引入粒子群算法并基于混沌变异思想，提出维多样性的动态权重粒子群算法.通过与其它三种不同定权方式的粒子群算法进行比较，证明该方法具有较好的稳定性和有效性，能以较快的速度收敛到最优解.利用河西地区1999-2001年GPS观测资料，对祁连山断裂、海原断裂和六盘山断裂的三维滑动速率进行了位错模式的维多样性动态权重粒子群算法反演，并在反演结果的基础上进行正演分析，结果表明，该方法可有效的求解出断层三维滑动速率，其反演结果与地质方法和前人的研究结果具有较好的一致性.
关键词： 粒子群算法     维多样性     动态权重     位错模型     断层滑动    
Slip velocity of fault induced by PSO algorithm with dynamical inertial weight and dimension mutation
WANG Shuai, ZHANG Yong-zhi, JIANG Yong-tao, LIU Ning    
School of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China
Abstract: Based on the chaotic mutation ideas,a new particle swarm optimization (PSO) algorithm with dimension diversity and dynamical inertial weight vector is introduced. Comparisons with other three PSO algorithms with different ways of fixed weight are made,which demonstrates that this new method is optimal stability and effectiveness and also possesses with faster convergence speed.Based on the GPS data of Hexi area observed from 1999 to 2001, the slip velocity of Qilianshan, Haiyuan faults and Liupanshan are inversed by this new PSO algorithm, what's more, based on the inversion results,forward analysis are carried out. Results show, this new method can be effectively to solve the fault slip velocity, which have a good consistency with the results that calculated by geological and other methods.
Key words: PSO algorithm     dimension diversity     dynamical weight     dislocation model     fault slip    
0 引 言

反演算法在大地测量反演中扮演着重要的角色，结合地质、地震和地球物理资料，以大地测量观测数据为基础，根据地球物理学建立的先验地球动力学模型，反演研究断层的滑动速率及活动板块的运动情况，进一步推求动力学模型参数、修正或提出新的地球动力学模型，对探讨地壳运动与地震的关系和地震、地质灾害的预测预报有着重要的意义(张永志，2011). 国内学者对反演算法及其在大地测量和地震学中的应用进行了广泛的研究，刘喜武等(2004)提出了高分辨率Radon变换的地震资料处理方法，显著提高了反演算法的效率和分辨率；朱守彪和蔡永恩(2006)将遗传算法与Marquardt法相结合反演了台湾地区地壳、地幔的粘性系数；温扬茂和许才军(2009)基于敏感度迭代拟合法(SBIF)反演了西藏玛尼地震的滑动分布；宋维琪等(2013)研究了微地震贝叶斯差分的进化反演方法；刘宁和张永志(2009)进行了断层滑动速率的蚁群算法反演，这些研究取得了丰硕的成果.粒子群算法(PSO)在大地测量反演中也得到了广泛的应用，刘杰等(2010)进行了断层三维滑动速率的粒子群算法反演，但解的收敛性不足；段虎荣等(2010)用改进的粒子群算法进行了同样的研究，虽然解的收敛性有所改善，但收敛速度仍然较慢.因此，为增强解的收敛性和提高解的收敛速度，在对经典粒子群算法深入研究的基础上，本文提出了维多样性的动态权重粒子群算法(DDMWPSO)，根据粒子维多样性采用混沌策略对粒子进行变异，通过不同粒子各维权重的自适应调整，进行最优解的搜索.

1 维多样性的动态权重粒子群算法

1.1 动态权重粒子群算法

杨维和李歧强(2004)对粒子群算法进行了综合论述，并给出了D维粒子i的位置和速度更新模型为

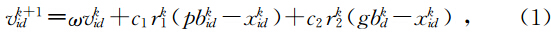
式中，vkid和xkid分别为粒子i在第k次迭代中第d维的速度和位置，pbkid为粒子i在k次迭代过程中第d维的最优位置，gbkd为整个粒子群在k次迭代过程中第d维的最优位置，ω为惯性权重；d=1，2，…D；c1、c2为学习因子；r1、r2为[0，1]之间均匀分布的随机数. 王洪涛和任燕(2011)给出了(1)式的矢量形式：

其中 α =c1r1(pbi－xi)+c2r2(gb－xi)表示由各维中pbi和gb合成的优势向量，在粒子速度更新过程中起向导作用. 分析图 1可知(v best为第k+1次迭代时粒子速度的理论最优值，v next为第k+1次迭代时粒子速度的实际最优值，v new为第k次迭代时粒子速度的实际最优值)，在粒子搜索过程中，通过 α和v new在第j维上的比值给出的该维上惯性权重ωj的取值策略.
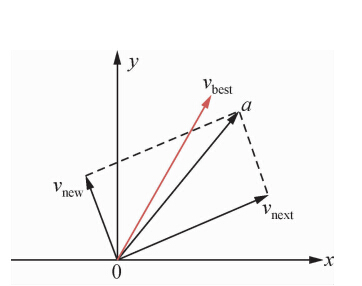图 1 粒子速度更新 Fig. 1 Velocity update

可以调整、控制粒子的速度，使粒子更好的向优势解靠近并接近最佳速度 v best.式(4)是一种新的自适应惯性权重策略(王洪涛和任燕，2011)：

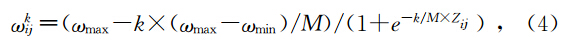
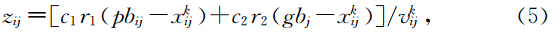
其中：M表示总的迭代次数，k表示当前迭代次数，ωmax和ωmin分别为最大和最小惯性权重，本文取其经验值，分别为0.9和0.1. 1.2 混沌变异策略

起始阶段，粒子群在每一维上的分布都不同，随着迭代的进行，粒子群在每一维上趋于聚集，粒子聚集或分散的程度可以用维多样性来描述.定义粒子群在第j维上的多样性用该维上位置的平均间距来表示(梁昔明等，2011)为

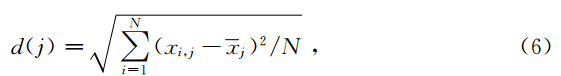
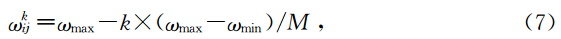
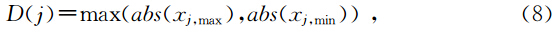
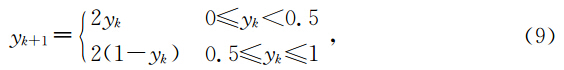
其中，N为粒子数目，xi，j为第i个粒子在第j维上的值，x j为所有粒子在第j维上的坐标均值，d(j)越小，说明粒子在第j维上的多样性就越差. 考虑到算法迭代到一定次数时粒子的维多样性变差，可能陷入局优，如果依然采用(4)式的权重策略可能会造成重复搜索，因此，在迭代到一定次数后，采用线性递减权重策略(7)式，构成新的混沌权重策略(骆晨钟和邵惠鹤，2000).当迭代次数达到总迭代次数的1/2时，对权重策略进行转换，且若维多样性小于阀门值时D(j)，根据Tent映射(式9)(王洪涛和任燕，2011)对粒子进行重新初始化.

其中，xj，max，xj，min为第j维粒子坐标的上下限，abs()为取绝对值函数.Tent映射具有很好的全局遍历性和均匀性，而且对初值敏感性不强，这样既将混沌搜索的全局遍历性、随机性和规律性引入了算法，又保持了前期搜索结果，提高了算法防早熟收敛及其全局搜索的能力.其在第j维上的变异步骤如下(王洪涛和任燕，2011)： (1)初始化利用(gbj－aj)/(bj－aj)将gbj变化为混沌变量zz1j； (2)产生混沌序列将zz1j作为初始值，利用公式(9)产生第j维的序列zz2j，zz3j，…zzNj； (3)形成所有粒子新的第j维将zzij利用aj+(bj－aj)×zzij得到xij，其中i=1，2，…N. 其中，bj和aj分别为粒子搜索过程中设定的第j维位置的上下限.按照(1)式和(2)式，对重新初始化后的粒子，进行迭代计算，即可求出满足相应迭代条件的粒子最优解. 2 模拟实验及分析

本例基于矩形位错模型(Okada， 1985，1992)和地表位移的关系，采用表 1给出的断层参数计算断层滑动引起的地表水平位移，并在结果中加入随机噪声作为GPS观测数据中由于各种原因带来的误差，依此检验算法的抗噪能力.最后用本文提出的DDMWPSO算法和其他三种不同定权方式的PSO算法对断层滑动速率进行反演，在搜索过程中，设定走滑速率、倾滑速率和张裂速率的上下限分别为[-20，20]、[-15，15]和[-15，15]，最大迭代次数为50，并根据目标函数(10)式(n为GPS测站数)判定粒子的适应度.

同时，从迭代到一定次数时反演结果的均值和最优值的大小这两个方面对算法的稳定性和有效性进行评价.结果如图 2和3(U1、U2和U3分别代表走滑、倾滑和张裂分量)所示.
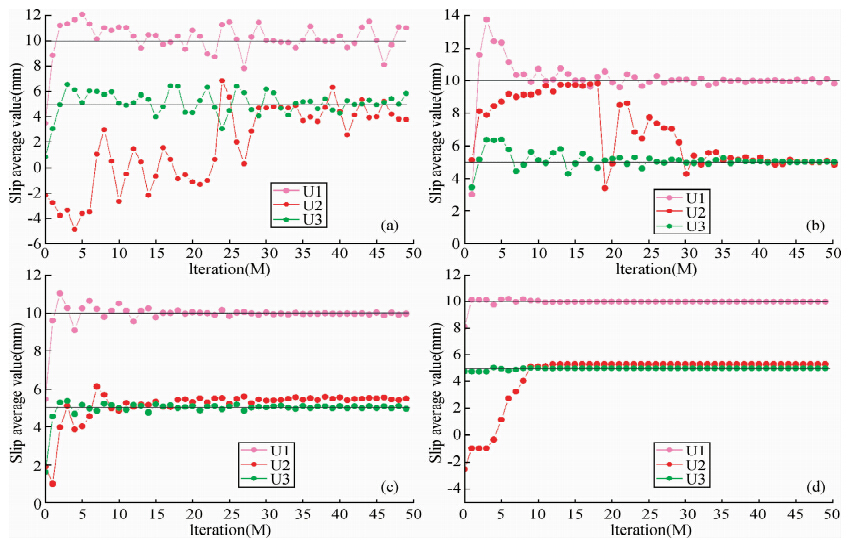图 2 滑动速率均值与迭代次数关系图(a)经典的PSO；(b)线性权重的PSO；(c)非线性的动态权重PSO；(d)维变异的动态权重PSO，

为方便描述，这四种方法分别简记为a、b、c和d. Fig. 2 The relationship between iterations and slip mean value (a)classical PSO;(b)linear weight PSO;(c)non-linear PSO;(d)DDMWPSO，shorth and these four methods by a、b、c、d，respectively.

表 1 模拟断层参数 Table 1 Fault parameters

从图 2可以看出，方法a和b得到的滑动速率均值只能达到局部最优，且收敛性较差；而利用方法c和d计算能以较快的速度收敛到最优解，但迭代次数在15~36之间时，方法c会出现一定的波动，且 将这两种方法相比可知，方法d的稳定性优于方法c；同时，从图 2中易知，当迭代次数为10次时，方法d已几乎搜索到全局最优解，而其他三种方法仍在 继续搜索，由此表明，方法d寻求最优解的收敛速度最快.可见，在给定有限的迭代次数内，利用方法d反演得到的结果均值最接近全局最优解，算法具有较好的稳定行和收敛性. 从图 3可以看出，方法a和b的收敛速度几乎相同，但都没有收敛到最优解；而方法c和d都反映出算法本身具有较好的全局搜索能力，但方法c在迭代前期会出现一定的波动，而后者表现出较好的稳定性，与图 1中c、d相吻合；当迭代到第10次时，d方法几乎已收敛到最优解而其他方法仍在搜索，说明DDMWPSO算法具有较快的收敛速度，同时，图 2d)表明DDMWPSO算法在整个求解过程中具有较好的稳定性和有效性.

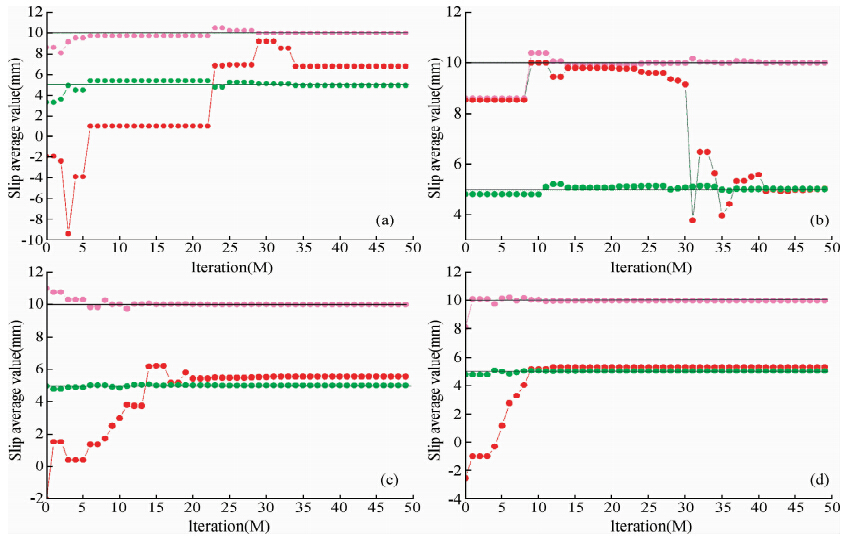图 3 滑动速率最优值与迭代次数关系图 (a)经典的PSO；(b)线性权重的PSO；(c)非线性的动态权重PSO；(d)维变异的动态权重PSO.

为方便描述，这四种方法分别简记为方法a、b、c和d. Fig. 3 The relationship between iterations and slip optimally value (a)classical PSO;(b)linear weight PSO;(c)non-linear PSO;(d)DDMWPSO，shorth and these four methods by a、b、c、d，respectively.

综上验证了DDMWPSO算法的稳定性和有效性.值得说明的是当求解粒子的维数增加时，相对于其他三种算法，该方法的优越性更为显著. 3 河西地区断裂滑动速率反演

河西地区近NW走向的祁连山断裂、海原断裂和六盘山断裂是青藏高原东北缘活动断裂带的重要组成部分，构成了青藏高原NE向运动的前缘地带，是我国构造运动最活跃的地区之一.鉴于DDMWPSO算法的优越性，现利用河西地区1999-2001年的GPS观测数据对该区祁连山断裂、海原断裂和六盘山断裂的三维滑动速率进行反演，以便深入地理解该区地壳运动和形变与活动断裂带的关系. Fu和Sun(2004)和张永志等(2009)均指出实际计算中应考虑断层滑动的不均匀性，特别是在近场区域断层滑动分布的不均匀性影响更为显著.为了精细刻划断层模型，减小模型误差，本文采用断层微分思想将祁连山断裂带、海原断裂带和六盘山断裂带分成17个子断层(表 2所示，其中：Q 表示祁连山断裂带，H表示海原断裂带，L表示六盘山断裂带).让40个粒子在随机解空间中进行最优解的DDMWPSO 算法搜索，最后得到祁连山断裂带、海原断裂带和六盘山断裂带的三维滑动速率(表 2). 从表 2断层滑动速率的反演结果可以看出，祁连山断裂带、海原断裂带和六盘山断裂带的滑动速率在空间上表现出不均匀性的特征.祁连山断裂带断层活动形式复杂，不同段断层呈现出不同的滑动性质，相对走滑方向，在倾滑和张裂方向上祁连山断裂滑动速率略大，与前人(张希等，2007；刘宁和张永志，2009)研究成果基本一致，且与地质学方法(丁国瑜等，1991)得出的祁连山北缘断层的垂直位错速率为2.26 mm/a，水平滑动速率值为1.3 mm/a相吻合；海原断裂表现出明显的左旋走滑运动兼有挤压的性质，最大走滑量可达-3.0 mm/a，最大挤压量可达-0.5 mm/a，与李强等(2013)研究结果相一致，此外，倾向方向上断层也存在明显的滑动，最大值可达0.8514 mm/a；与海原断裂带相似，六盘山断裂带同样表现出走滑兼挤压的滑动特征，在倾向方向上六盘山断裂带由西向东呈现出正倾滑-逆冲-正倾滑-逆冲的构造转换样式.表 2断层滑动速率体现出祁连山断裂带、海原断裂带和六盘山断裂带构造活动的分段变化性，进一步解释了青藏高原东北缘活动断裂带复杂的构造运动背景.

表 2 断层滑动速率反演结果 Table 2 Inversion results of fault sliding by DDMWPSO

为进一步验证DDMWPSO算法反演得到的断层滑动速率的有效性，基于矩形位错模型，通过表 2反演结果，计算了河西地区祁连山断裂带、海原断裂带和六盘山断裂带断层活动产生的地表水平形变场，并和该区1999-2001年的GPS观测结果进行对比(图 4)，可以看出：整个区域，模拟值与观测值在大小和方向上都体现出了较好的一致性，模拟结果与GPS观测结果的差异主要反映在模拟结果只是所研究断层活动引起的变形，而观测结果反映了断层活动与区域动力学过程的整体变形；分析图 4可知，河西地区地壳水平运动呈现显著的顺时针旋转运动特征，这与青藏高原在印度板块北-北东向的推挤作用下，其东北缘的NE向运动受到阿拉善和鄂尔多斯块体阻挡的区域动力学背景密切相关.可见，维多样性的动态权重粒子群算法可以较好的反演出断层的滑动速率.

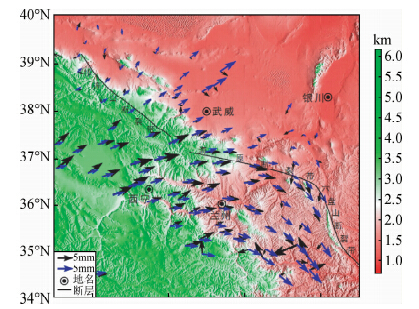图 4 河西地区1999-2001水平运动速率， 黑色箭头为GPS观测值，蓝色箭头为 模拟值.单位：mm/yr. Fig. 4 Horizontal velocities of Hexi area from 1999- 2001，black arrows denote observation values， blue arrows denote simulation values.Unites:mm/yr.
4 认 识

基于反演算法和地球动力学模型，利用GPS等大尺度空间观测数据研究断层三维滑动速率，对区域构造变形的动力学解释、探究地震孕育的过程和地震活动的预测有着重要的意义.本文提出维多样性的动态权重粒子群算法反演断层三维滑动速率，有以下几点认识： (1)基于维多样性混沌变异思想的维多样性动态权重粒子群算法，通过不同粒子各维权重的自适应调整，能够以较快的速度收敛到最优解，具有良好的稳定性和有效性. (2)祁连山断裂带不同段呈现出不同的滑动性质；海原断裂带表现出走滑兼挤压的运动特征，且存在一定的倾滑分量；与海原断裂带相比，六盘山断裂带不同点主要体现在倾向方向上，自西向东呈现出正倾滑-逆冲-正倾滑-逆冲的构造转换样式；祁连山断裂带、海原断裂带和六盘山断裂带的构造活动具有分段变化性. (3)基于DDMWPSO算法得出的断层滑动速率结果计算出的位移场与GPS观测值，在大小和方向上都体现出了较好的一致性，维多样性的动态权重粒子群算法可有效的求解出断层三维滑动速率.

致 谢 感谢审稿专家提出的宝贵修改意见.

参考文献
[1] Ding GY. 1991. Lithospheric Dynamics of China(in Chinese) [M].Beijing: Seismology Press.
[2] Duan HR, Zhang YZ, Xu HJ. 2010. Improved particle swarm optimization algorithm and its application in inversion of slip velocity of fault[J]. Journal of Geodesy and Geodynamics (in Chinese), 30(6): 31-36.
[3] Fu G Y, Sun W. 2004. Effects of spatial distribution of fault slip on calculating co-seismic displacement: Case studies of the Chi-Chi earthquake (MW 7.6) and the Kunlun earthquake (MW 7.8) [J]. Geophysical Research Letters, 31(21): L21601.
[4] Li Q, Jiang ZS, Wu YQ, et al. 2013. Present-day tectonic deformation characteristics of Haiyuan-Liupanshan fault zone[J]. Journal of Geodesy and Geodynamics(in Chinese), 33(2): 18-22.
[5] Liang XM, Dong SH, Long W, et al. 2011. PSO algorithm with dynamical inertial weight vector and dimension mutation[J]. Computer Engineering and Applications(in Chinese), 47(5): 29-31.
[6] Liu J, Zhang YZ, Zhang XX, et al. 2010. Fault slip velocity inversion by using particle swarm optimization algorithm from GPS data [J]. Journal of Geodesy and Geodynamics(in Chinese), 30(2): 40-42.
[7] Liu N, Zhang YZ. 2009. Fault parameter inversion with ant colony algorithm by dislocation model[J]. Journal of Geodesy and Geodynamics(in Chinese), 29(1): 52-56.
[8] Liu X W, Liu H, Li Y M. 2004. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics (in Chinese), 19(1): 8-15.
[9] Luo CZ, Shao HH. 2000. Evolutionary Algorithms with Chaotic Mutations[J]. Control and Decision(in Chinese), 15(5): 557-560.
[10] Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 75(4): 1135-1154.
[11] Okada Y. 1992. Internal deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 82(2): 1018-1040.
[12] Song WQ, Gao YK, Zhu HW. 2013. The differential evolution inversion method based on Bayesian theory for micro-seismic data[J]. Chinese J. Geophys. (in Chinese), 56(4): 1331-1339, doi:10.6038/cjg20130427.
[13] Wang HT, Ren Y. 2011. Particle swarm optimization algorithm based on modified inertia weight[J]. Computer Applications and Software (in Chinese), 28(10): 271-274.
[14] Wen YM, Xu CJ. 2009.MS 7.9 Mani earthquake slip distribution inversion by a sensitivity-based iterative fitting method[J]. Geomatics and Information Science of Wuhan University(in Chinese), 34(6): 732-735.
[15] Yang W, Li QQ. 2004.Survey on particle swarm optimization algorithm [J].Engineering Science(in Chinese), 6(5): 87-94.
[16] Zhang X, Jiang ZS, Wang SX, et al. 2007. United inversion of three-dimensional negative dislocation for GPS and leveling observation in northeastern margins of Qinghai-Tibet block[J]. Recent Developments in World Seismology(in Chinese), (7): 61-66.
[17] Zhang YZ, Zhao DJ, Wang WD. 2009. Effects on the earth surface deformation by asymmetric strike slip on fault plane[J].Chinese J. Geophys.(in Chinese), 52(8): 2113-2118.
[18] Zhang YZ. 2011. Dislocation theory and its application in the study of the deformation of the earth(in Chinese) [M].Xi'an:Xi'an JiaotongUniversity Press.
[19] Zhu S B, Cai YE. 2006. Inversion of viscous properties of crust and mantle from the GPS temporal series measurements[J]. Chinese J. Geophys. (in Chinese), 49(3): 771-777.
[20] 丁国瑜.1991.中国岩石圈动力学概论[M].北京:地震出版社
[21] 段虎荣, 张永志, 徐海军. 2010. 改进的粒子群算法在断层滑动速率反演中的应用[J]. 大地测量与地球动力学, 30(6): 31-36.
[22] 李强, 江在森, 武艳强,等. 2013. 海原-六盘山断裂带现今构造变形特征[J]. 大地测量与地球动力学, 33(2): 18-22.
[23] 梁昔明, 董淑华, 龙文,等. 2011. 动态惯性权重向量和维变异的粒子群优化算法[J]. 计算机工程与应用, 47(5): 29-31.
[24] 刘杰, 张永志, 张秀霞,等. 2010. 基于 GPS 数据的粒子群算法反演断层三维滑动速率[J]. 大地测量与地球动力学, 30(2): 40-42.
[25] 刘宁, 张永志. 2009. 位错模式的蚁群算法反演断层参数[J]. 大地测量与地球动力学, 29(1): 52-56.
[26] 刘喜武, 刘洪, 李幼铭. 2004. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 19(1): 8-15.
[27] 骆晨钟, 邵惠鹤. 2000. 采用混沌变异的进化算法[J]. 控制与决策, 15(5): 557-560.
[28] 宋维琪, 高艳珂, 朱海伟. 2013. 微地震资料贝叶斯理论差分进化反演方法[J]. 地球物理学报, 56(4): 1331-1339, doi:10.6038/cjg20130427.
[29] 王洪涛, 任燕. 2011. 基于改进惯性权重的粒子群优化算法[J]. 计算机应用与软件, 28(10): 271-274.
[30] 温扬茂, 许才军. 2009. 基于敏感度的迭代拟合法反演玛尼 MS 7.9 级地震滑动分布[J]. 武汉大学学报: 信息科学版, 34(6): 732-735.
[31] 杨维, 李歧强. 2004. 粒子群优化算法综述[J]. 中国工程科学, 6(5): 87-94.
[32] 张希, 江在森, 王双绪,等. 2007. 青藏块体东北缘 GPS 与水准资料的三维负位错联合反演[J]. 国际地震动态, (7): 61-66.
[33] 张永志, 赵大江, 王卫东. 2009. 断层走滑不均匀性对地面变形的影响[J]. 地球物理学报, 52(8): 2113-2118.
[34] 张永志.2011.位错理论及其在大地变形研究中的应用[M].西安: 西安交通大学出版社.
[35] 朱守彪, 蔡永恩. 2006. 利用GPS观测的时间序列资料反演地壳地幔黏性结构[J]. 地球物理学报, 49(3): 771-777.