2014, Vol. 29
2. 西北大学数学系, 西安 710127
2. Mathematics Department of Northwest University, Xi'an 710127, China
地震数值模拟在油气藏的勘探开发中正发挥着越来越重要的作用.通过地震波场数值模拟(Kelly et al., 1976；Chen，1984； Dablain，1986；Fei and Larner， 1995；Komatitsch and Vilotte， 1998；董良国等，2000；Ma et al., 2003； 殷文等，2006； 朱生旺等，2007)，人们可以探索地震波传播机理、验证修改解释方案、进行地震反演研究等.加深对地震波在复杂介质中传播规律的认识，检验地震勘探方法技术(地震采集、处理与解释)的适用性.这对于地震采集施工设计，地震资料的处理、解释以及地震勘探后的岩性评价都具有重要意义.随着三维地震勘探的广泛应用及复杂介质精细成像的普遍开展，研究高效的正演模拟数值方法非常必要.
弹性波方程的正演数值模拟技术一直是地球物理学中非常重要的研究课题.弹性波数值模拟技术发展非常迅速，20世纪以来，弹性波数值模拟方法已经有有限差分法(Kelly et al., 1976；Dablain，1986)、伪谱法(Komatitsch and Vilotte， 1998)、有限元法(Chen，1984)、辛算法(Ma et al., 2003)等，这些方法都有各自的优点和不足.
有限差分法因为其编程易实现、计算迅速等优点在地震数值模拟中得到广泛应用.董良国等(2000)提到使用传统的显式差分格式进行波动方程求解时，会因为数值波速与真实波速的不同步，在粗网格情况下产生假波，引起严重的数值频散，使得人们难以辨别真假波，失去了正演模拟计算的意义.为了克服有限差分方法存在的数值频散问题，(Kondoh et al., 1994； Yang et al., 2003； Yang et al., 2006； Yang et al., 2007； 王磊等，2009； Yang et al., 2009)采用了一些方法，这些方法均具有良好的压制数值频散的效果.但这些方法均为非辛格式，为了进行数值模拟都人为的引进一定的数值耗散.
地震波传播过程本质上是能量在传播过程中不断损耗直到殆尽的过程，而在实际应用中，常在无能量损耗的假设下，用弹性波方程描述(罗明秋等，2001).所以，地震波在地球介质中的传播过程可以看成一个保守无耗散的过程，而一切耗散效应可以忽略的方程都可以写成哈密顿偏微分方程的形式.由冯康先生开创的Hamilton 系统的辛几何算法发展至今，在理论上已较为完善.由于这一算法具有长时间的数值稳定性，能够很好地保持Hamilton 系统的辛几何结构的性质，在现代物理学和力学研究中发挥着重要作用.马等应用辛可分Runge-Kutta 方法对波动方程进行了研究，这种方法具有有效压制数值频散，计算快速以及低存储要求等优良的性质.但用此方法对偏微分方程进行辛离散时具有局限性，具体表现在此方法是个全局性的概念.为克服此局限性，Bridges和Reich引入了一个保持守恒型偏微分方程局部多辛结构的多辛积分的概念(Moore and Reich， 2003； Ascher and McLachlan， 2004；Islas and Schober， 2005).在实际研究与实践中，有许多问题需要进行长时间的数值模拟计算，因此，对具有长时间数值行为的辛算法的研究具有重要的理论与实际意义，并且取得了丰硕的研究成果.本文研究一类在石油勘探中具有重要意义的单相各向同性介质中的弹性波方程
其中u，v，w分别为x，y，z方向的位移分量，λ，μ为Lamé常数，ρ为介质密度常数，f1，f2，f3表示x，y，z方向上的力源分量，在二维x-y情况下，可得到v和u，w相分离的方程
许多作者对系统(2)做了一些数值方面的研究，殷等用有限差分法对弹性波方程(2)进行了数值模拟，(王书强等，2002)用紧致差分法对弹性波方程(2)进行了数值模拟，都得到了不错的数值结果，但是这些研究都是非辛数值方法，都带有人为的耗散性，在经过长时间的数值模拟时，都会失真，都不能完全保持原来的物理性质.本文应用保结构算法(Chen，2005)(多辛算法)来研究弹性波方程，这种算法是一种干净的算法，不带有人为的耗散性，能保持原来的物理性质.本文在第二节里给出了单相各向同性介质中的弹性波方程的多辛结构.在第三节里验证了单相各向同性介质中的弹性波方程具Hamilton 多辛格式，并证实此格式具有多辛守恒律、局部能量守恒律、动量守恒律.第四节给出了单相各向同性介质中的弹性波方程的离散中心Preissmann多辛格式，并证实此格式在离散格式下忍保持多辛守恒律、局部能量守恒律、动量守恒律.在第五节给出了一个数值模拟，验证了本文的算法不仅简单，而且有长时间的稳定性. 1 弹性波方程的多辛几何结构
为了考虑弹性波方程的多辛几何结构，我们首先定义弹性波方程(2)的斜变空间为X×U其中X=(x，y，t)，U=(u，v，w)，然后我们可以定义弹性波方程(2)的斜变空间X×U的一阶延拓为
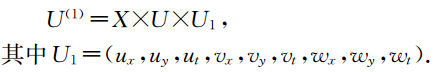
设φ=(u，v，w):X→U，我们定义φ的一阶延拓为
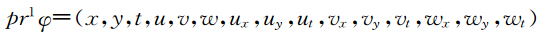
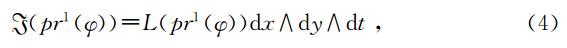
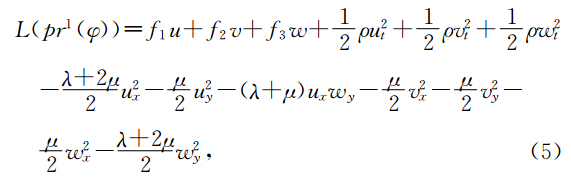
设 V 是弹性波方程(2)的斜变空间X×U为的一个向量场，且
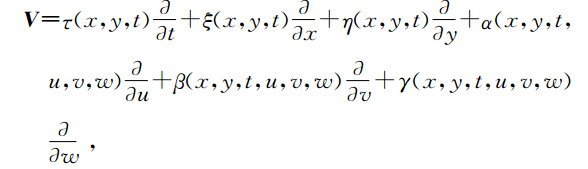
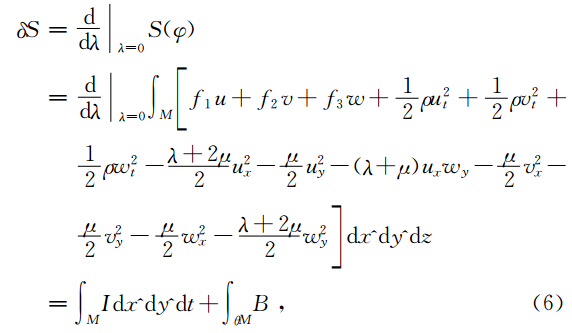
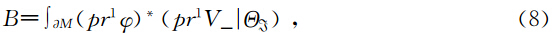
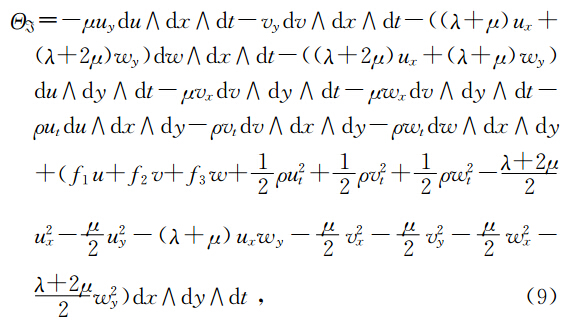
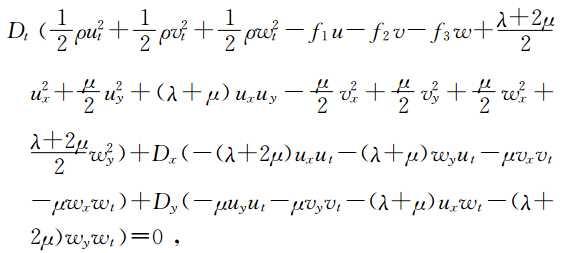
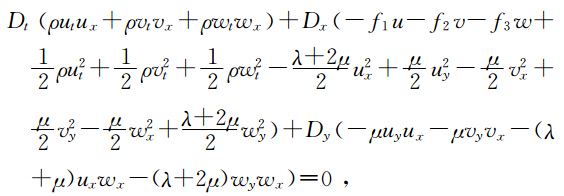
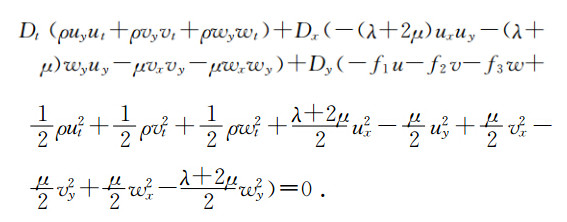
Bridges 首先提出了一切耗散效应可以忽略的方程都可以写成多辛Hamilton系统(多辛偏微分方程组)，实践证明，许多数学物理方程都可以写成多辛偏微分方程组形式为
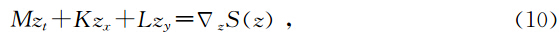
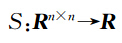
这种形式(10)具有很多优点，第一，系统(10)具有多辛守恒律为
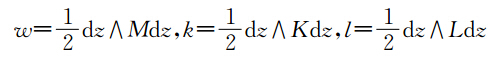
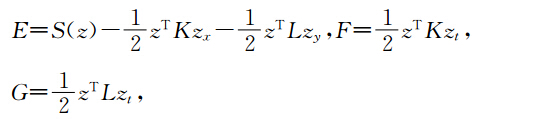
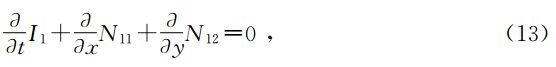
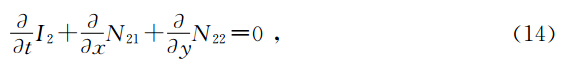
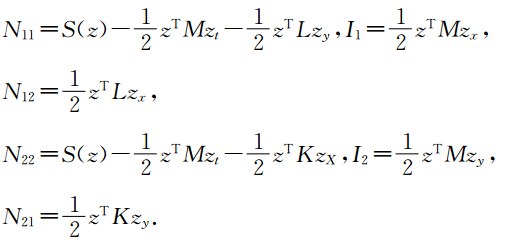
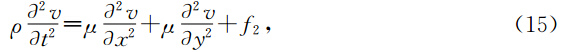
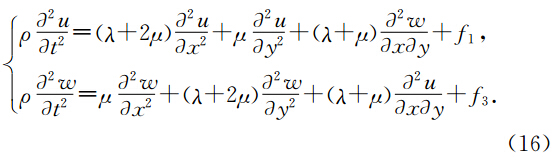
我们首先解方程(15)，对方程(15)引入正则动量
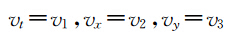
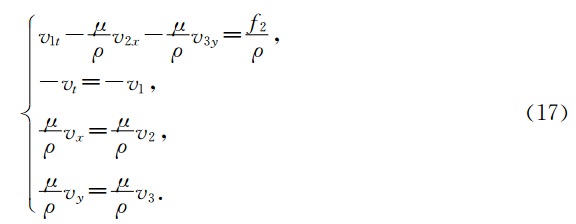
定义状态变量：z=(v，v1，v2，v3)， 方程(15)可以写成多辛方程组(10)的形式，其中
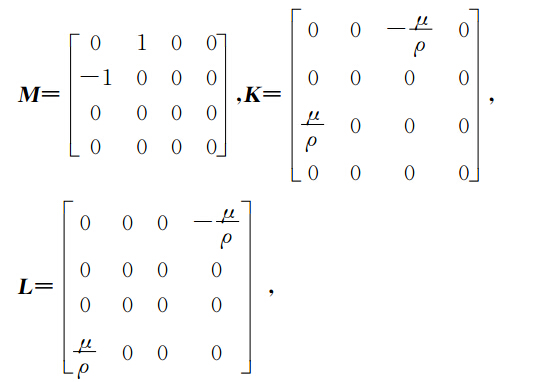
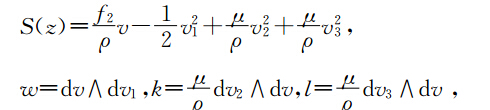
通过计算，方程(15)的等价形式(17)具有局部能量守恒律(12)，其中有
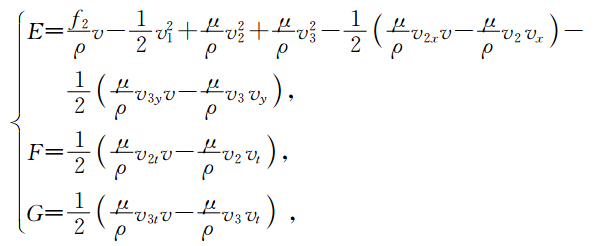
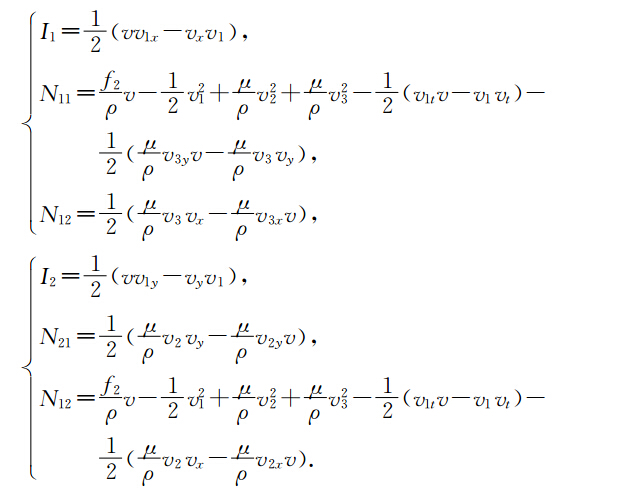
下面我们用同样的方法建立方程(16)的多辛形式、多辛守恒律、多辛局部能量守恒律和局部动量守恒律.对方程(16)引入正则动量有
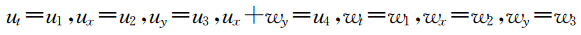
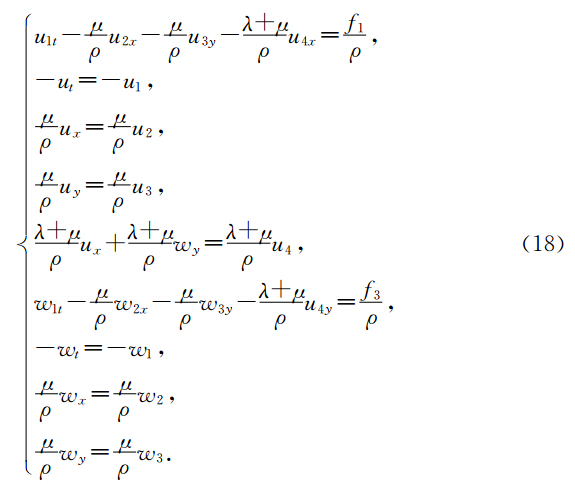
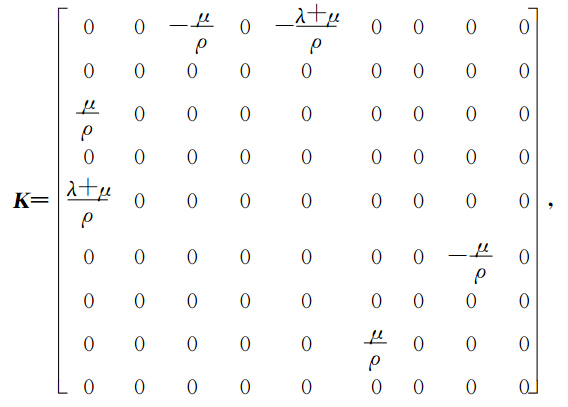
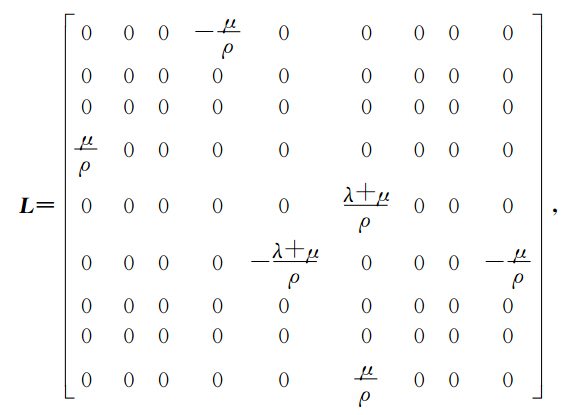
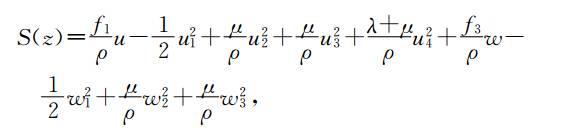
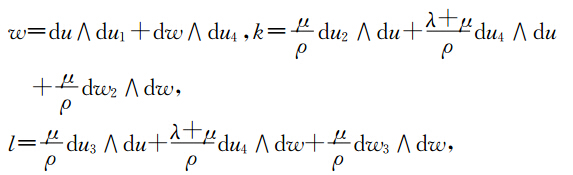
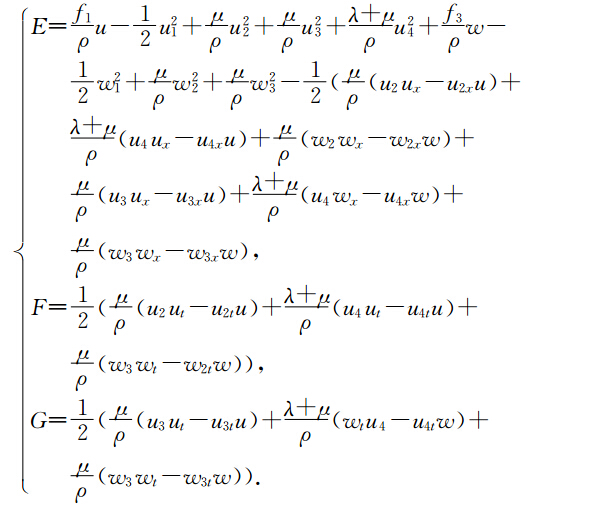
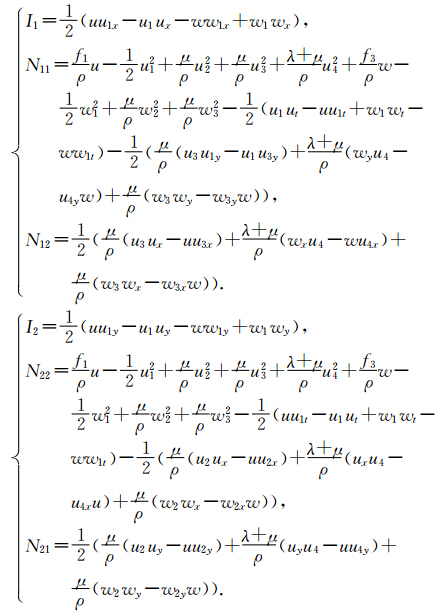
通过上面的分析，最终我们把弹性波方程分解为两个一阶多辛偏微分方程组.由于这两个偏微分方程组都是多辛形式.因此这两个偏微分方程具有多辛守恒律、多辛局部能量守恒律和多辛局部动量守恒律.下面我们建立这两个方程的离散多辛格式，并验证这种离散形式具有离散多辛守恒律、多辛局部能量守恒律和多辛局部动量守恒律. 3 弹性波方程的多辛Preissmann格式及离散守恒律
多辛形式的一个重要性质是它的局部守恒的概念.多辛是Hamilton偏微分方程的一个几何性质，当构造一种数值格式时，我们希望多辛守恒律能保持下来，Bridge和Reich称能保持离散多辛守恒律的格式为多辛格式.下面我们建立方程(17-18)的多辛格式.
多辛Hamilton系统(10)的中心Preissmann格式可表示为(王俊杰等， 2012a，2012b，2012c; Wang and Wang， 2013)
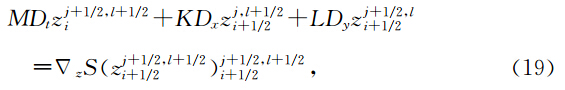
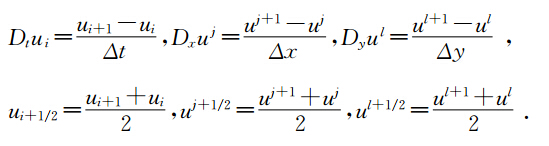
定理1 数值方法(19)为多辛积分，且满足如下离散多辛守恒律为
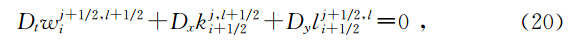
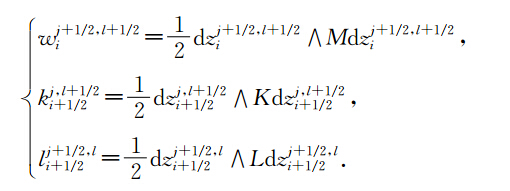
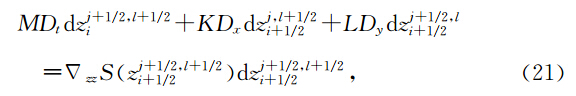
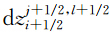做外积，注意到有
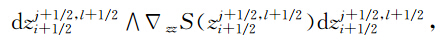
得到离散守恒律(20).
在一般情况下，方程(19)不能保持局部能量守恒律，但当S(z)= 1 2 zTAz或者S(z)= 1 2 zTAz和一个线性项的和时，中心Preissmann格式满足离散局部能量守恒律，动量守恒律.
定理2(.T.JBridges et al., 2001)如果Hamilton函数S(z)可以表示为S(z)= 1 2 zTAz或者S(z)= 1 2 zTAz 一个线性项的和时，其中A为对称矩阵，则中心Preissmann多辛格式离散局部能量守恒律为：
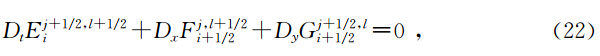
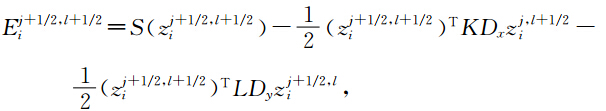
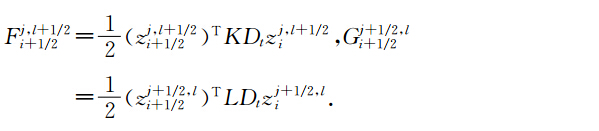
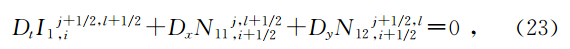
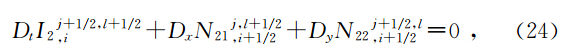
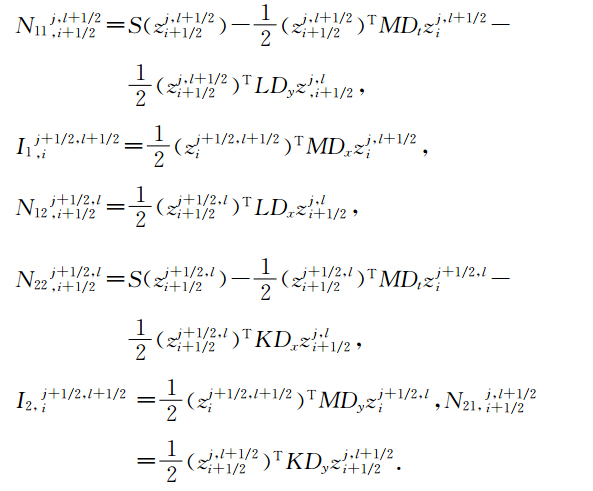
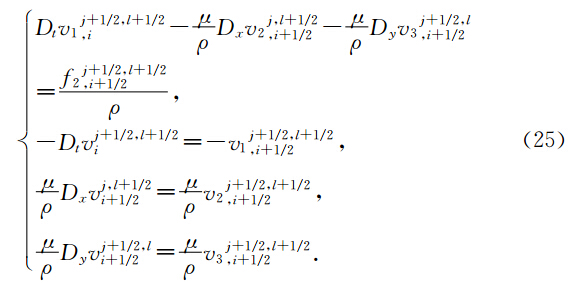
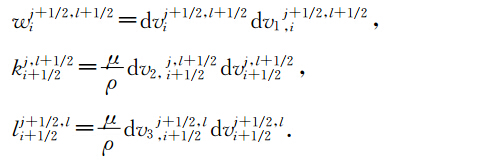
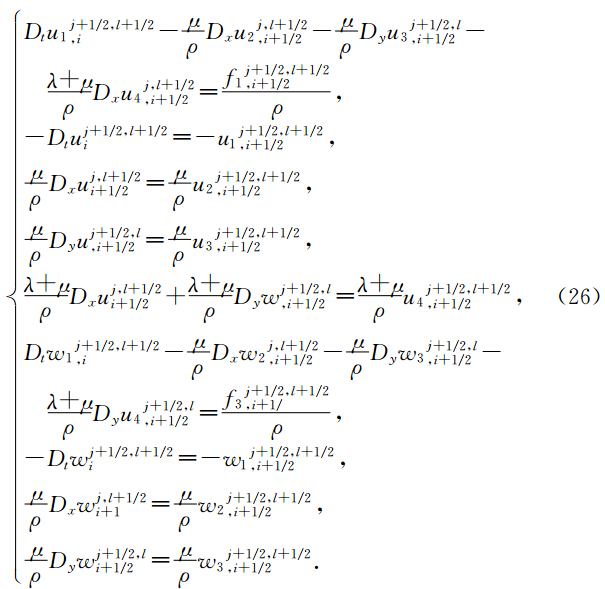
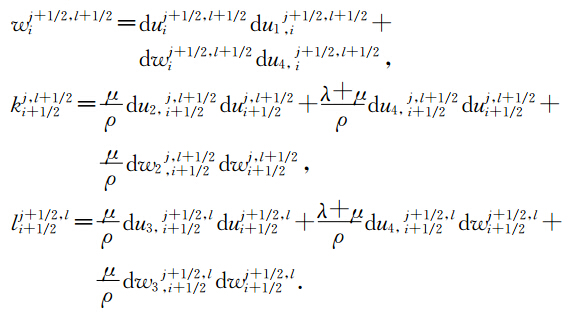
下面我们建立方程(17-18)的离散多辛局部能量守恒律，多辛局部动量守恒律，当f1=f2=f3=0时，方程(17-18)的Hamilton函数S(z)可以表示为S(z)= 1 2 zTAz，当f1，f2，f3≠0时，方程(17-18)的Hamilton函数S(z)可以表示为S(z)= 1 2 zTAz与一个线性项的和，所以方程(27-28)具有离散局部能量守恒律22，动量守恒律23-24.用类似于(胡莹莹等，2009)证明后误差分析的办法，可以得到本文算法具有精度°(Δt+(Δx2+Δy2)). 4 弹性波波场模拟
为了说明多辛方法的诸多优点，本文用中心Preissmann多辛格式(25-26)，来数值模拟单相各向同性介质中的弹性波方程，并且与差分法做一下对比.考虑下面单相各向同性介质中的弹性波方程初值问题为
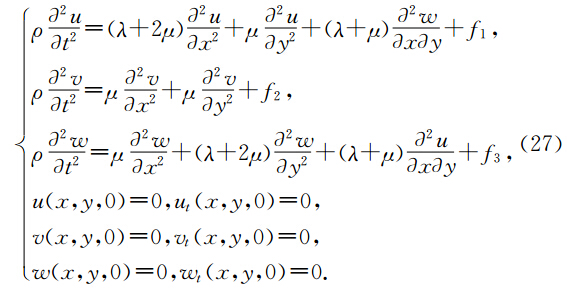
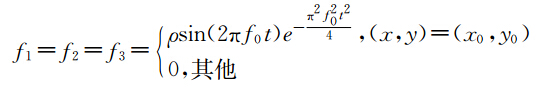
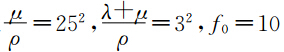Hz，震源位于区间x∈[0，5 km]，y∈[0，5 km]内，取时间步长Δt=0.0025空间步长Δx=Δy=0.01.下面我们应用中心Preissmann多辛格式来模拟上面的单相各向同性介质中的弹性波方程初值问题(27).
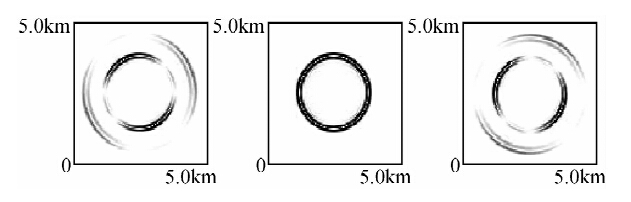 | 图 1 差分法的数值结果 Fig. 1 numerical solution of differential method |
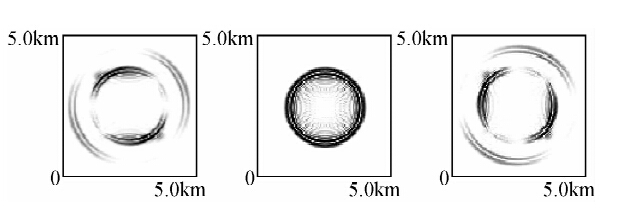 | 图 2 多心Preissmann法的数值结果 Fig. 2 numerical solution of multi-symplectic Preissmann method |
图 1，2是差分格式和中心Preissmann多辛格式计算到t=0.6 s时的波场快照.从图 2可以看出用中心Preissmann多辛格式进行数值模拟.u，w两图中的横波和纵波比较清晰，其结果显然比差分格式的结果要好.从图 2可以看出:波形和波速均没有随着时间的变化而变化这充分说明中心Preissmann多辛格式具有能够很好的保持解的基本几何性质;而且在整个模拟过程中，系统具有多辛守恒律、局部能量守恒律和动量守恒律.数值实验的结果表明:本文构造的多辛格式能够很好地模拟单相各向同性介质中的弹性波方程，同时能够很好地保持系统的多个守恒律，这些充分说明多辛方法具有以下两大优点:良好的长时间数值行为和精确地保持多种守恒律.
致 谢 感谢审稿专家提出的宝贵修改意见，感谢编辑部老师帮助.
| [1] | Ascher U M, McLachlan R I. 2004. Multisymplectic box schemes and the Korteweg-de Vries equation[J]. Applied Numerical Mathematics, 48(3-4): 255-690. |
| [2] | Bridges T J, Reieh S. 2001. Multi-symplectic integrators :numerical schemes for Hamiltonian PDEs that conserve sysmplecticity[J]. Phys. Lett. A, 284(4-5): 184-193. |
| [3] | Chen K H. 1984. Propagating numerical model of elastic wave in anisotropic in homogeneous media-finite element method[C]. Symposium of 54th SEG, 54: 631-632. |
| [4] | Chen J B. 2005. Multisymplectic geometry, local conservation laws and Fourier pseudospectral discretization for the good Boussinesq equation[J]. Appl. Math. Comput, 161(1): 55-67. |
| [5] | Dong G L, Ma Z T,Cao J Z. 2000. A staggered-grid high-order difference method of Vone-order elastic wave equation[J]. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419. |
| [6] | Dablain M A. 1986. The application of high-order differencing to the sclar wave equation[J]. Geophysics, 51(1): 54-66. |
| [7] | Fei T, Larner K. 1995. Elimination of numerical dispersion in finite difference modeling and migration by flux-corrected transport[J]. Geophysics, 60(6): 1830-1842. |
| [8] | Hu Y Y, Wang Y S, Wang H P. 2009. A new explicit multi-symplectic scheme for rlw equation[J]. Mathematica Numerica Sinica (in Chinese), 31(4): 349-362. |
| [9] | Islas A L, Schober C M. 2005. Backward error analysis for multisymplectic discretization of Hamiltonian PDEs[J]. Mathematics and Computers in Simulation, 69(3-4): 290-303. |
| [10] | Kelly K R, Wave P W, Treitel S. 1976. Synthetic seimograms: a finite-difference approach[J]. Geophysics, 41(1): 2-27. |
| [11] | Komatitsch D, Vilotte J P. 1998. The spectral element method: an efficient tool to simulate the seismic response of 2D and 3D geological structures [J]. Bull. Seism Soc. Am., 88(2): 368-392. |
| [12] | Kondoh Y, Hosaka Y, Ishii K. 1994. Kernel optimum nearly-analytical discretization (KOND)algorithm applied to parabolic and hyperbolic equation[J]. Computer Math. Appl., 27(3): 59-90. |
| [13] | Luo M Q, Liu H, Li Y M. 2001. Hamiltonian description and symplectic method of seismic wave propagation[J]. Chinese Journal of Geophysics (in Chinese), 44(1): 120-127. |
| [14] | Ma X, Yang D H, Zhang J H. 2010. Symplectic partitioned runge-kutta method for solving the acoustic wave equation[J]. Chinese Journal of Geophysics (in Chinese), 53(8): 1993-2003. |
| [15] | Moore B, Reich S. 2003. Backward error analysis for multi-symplectic integration methods[J]. Numerische Mathematik, 95(4): 625-652. |
| [16] | Wang J J, Wang L T, Yang K D. 2012a. Multi-symplectic preissmann methods for generalized zakharov-kuznetsov equation[J]. Journal of Atomic and Molecular Physics (in Chinese), 29(6): 1082-1090. |
| [17] | Wang J J, Wang L T, Yang K D. 2012b. Multi-symplectic Preissmann scheme for ZK-MEM equation[J]. Journal of Hangzhou Normal University (in Chinese), 11(5): 453-458. |
| [18] | Wang J J, Wang L T, Yang K D. 2012c. Multi-symplectic Preissmann methods to compute the variant Boussinesq equation[J]. Journal of Dynamics and Control (in Chinese), 10(2): 130-135. |
| [19] | Wang J J, Wang L T. 2013. Multi-symplectic Preissmann scheme for a high order wave equation of KdV type[J]. Applied Mathematics and Computation, 219(9): 4400-4409. |
| [20] | Wang L, Yang D H, Deng X Y. 2009. WNAD method for seismic stress-field modeling in he-terogeneous media[J]. Chinese Journal of Geophysics (in Chinese), 52(6): 1526-1535. |
| [21] | Wang S Q, Yang D H, Yang K D. 2002. Compact finite difference scheme for elastic equations[J]. J. Tsinghua Univ., 42(8): 1128-1131. |
| [22] | Yang D H, Teng J W, Zhang Z J, et al. 2003. A nearly-analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bull. Soc. Am., 93(2): 882-890. |
| [23] | Yang D H, Peng J M, Lu M, et al. 2006. Optimal nearly analytic discrete approximation to the scalar wave equation[J]. Bull. Seism. Soc. Am., 96(3): 1114-1130. |
| [24] | Yang D H, Song G J, Chen S, et al. 2007. An improved nearly analytical discrete method: an efficient tool to simulate the seismic response of 2-D porous structures [J]. J. Geophys. Eng., 4(1): 40-52. |
| [25] | Yang D H, Wang N, Chen S, et al. 2009. An explicit method based on the implicit Runge-Kutta algorithm for solving the wave equation[J]. Bull. Seism. Soc. Am., 99(6): 3340-3354. |
| [26] | Yin W, Yin X Y, Wu G Z, et al. 2006. The method of finite difference of high precision elastic wave equations in the frequency domain and wave-field simulation [J]. Chinese Journal of Geophysics (in Chinese), 49(2): 561-568. |
| [27] | Zhu S W, Qu S L, Wei X C, et al. 2007. Numeric simulation by grid-various finite-difference elastic wave equation[J]. Oil Geophysical Prospecting (in Chinese), 42(6): 634-639. |
| [28] | 董良国, 马在田, 曹景忠,等. 2000. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 43(3): 411-419. |
| [29] | 胡莹莹, 王雨顺, 王会平. 2009. RLM 方程的一个新的显式多辛格式[J]. 计算数学, 31(4): 349-362. |
| [30] | 罗明秋, 刘洪, 李幼铭. 2001. 地震波传播的哈密顿表述及辛几何算法[J]. 地球物理学报, 44(1): 120-127. |
| [31] | 马啸, 杨顶辉, 张锦华. 2010. 求解声波方程的辛可分Runge-Kutta方法[J]. 地球物理学报, 53(8): 1993-2003. |
| [32] | 王磊, 杨顶辉, 邓小英. 2009. 非均匀介质中地震波应力场的WNAD方法及其数值模拟[J]. 地球物理学报, 52(6): 1526-1535. |
| [33] | 王书强, 杨顶辉, 杨宽德. 2002. 弹性波方程的紧致差分方法[J]. 清华大学学报, 42(8): 1128-1131. |
| [34] | 王俊杰, 王连堂, 杨宽德. 2012a. 广义Zakharov-Kuznetsov方程的多辛Preissmann格式[J]. 原子与分子物理学报, 29(6): 1082-1090. |
| [35] | 王俊杰, 王连堂, 杨宽德. 2012b. ZK-MEM方程的多辛Preissmann格式[J]. 杭州师范大学学报, 11(5): 453-458. |
| [36] | 王俊杰, 王连堂, 杨宽德. 2012c. 变形Boussinesq方程组的多辛preissmann格式计算研究[J]. 动力学与控制学报, 10(2): 130-135. |
| [37] | 殷文, 印兴耀, 吴国忱,等. 2006. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 49(2): 561-568. |
| [38] | 朱生旺, 曲寿利, 魏修成,等. 2007. 变网格有限差分弹性波方程数值模拟方法[J]. 石油地球物理勘探, 42(6): 634-639. |