2. 地下信息探测技术与仪器教育部重点实验室(中国地质大学, 北京), 北京 100083
2. Key Laboratory of Geo-detection (China University of Geosciences, Beijing), Ministry of Education, Beijing 100083, China
0 引 言
磁力勘探中,磁测资料处理解释(如化磁极、分量换算、磁源重力异常换算、正演和反演等)通常需要已知场源的总磁化方向信息.总磁化方向是感应磁化方向和剩余磁化方向的矢量和.若岩矿石没有或剩磁不明显,且自退磁效应可忽略,则总磁化方向与感应磁化方向(即现代地磁场方向)基本一致.然而,在有强剩磁的存在下,总磁化方向明显改变,与感应磁化方向并不一致.此时,若直接利用现代地磁场方向作为总磁化方向进行磁测资料处理解释,会导致结果存在误差,与实际地质情况并不相符.
目前,除采集岩石标本并测定剩磁参数外,国内外学者提出了一些估计磁化方向的方法.唐俊德(1986)提出利用磁异常三分量确定磁化方向的圆曲线法;Roest和Pilkington(1993)提出基于磁场总梯度模和磁源重力异常水平梯度互相关的估计方法;Medeiros和Silva(1995)提出利用等效源磁矩反演估计磁化方向;甘西(2001)利用磁场的垂直分量确定磁性体磁化方向;Phillips(2005)给出估计磁化方向的Helbig(1963)积分法的直接算法和间接算法;Dannemiller和Li(2006)提出基于化极磁异常垂直梯度与总梯度模互相关的估计方法;Gerovska等(2009)提出基于化极磁异常与总模量磁异常互相关的估计方法.但目前这些方法仍存在一些实际问题和难题,如要求测区磁化方向相对固定不变,低纬度地区需要特殊稳定的低纬度化极方法,抗噪声或干扰能力较差等,至今没能得到广泛应用.
本文基于重磁三维相关成像的基本思路(Guo et al., 2011a,b; Guo et al., 2012),研究提出从磁总场异常估计磁化方向的新方法—偶极源互相关法,首先介绍该方法的基本原理,然后进行理论模型数据试验,并与Dannemiller方法的处理结果进行对比分析,最后利用我国西北某金属矿区实测航磁资料进行偶极源互相关法的有效性试验验证.
1 方法原理
在地形起伏测区,笛卡儿坐标(x,y)平面在基准面上,z取垂直向下为正.地下任意坐标为(xq,yq,zq)的第q个磁偶极源在测区任意点(x,y,z)处的理论磁总场异常ΔTq(x,y,z)可表示为
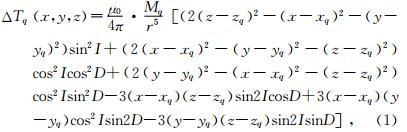
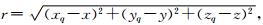 Mq为偶极源的磁矩,I和D分别是偶极源的总磁化方向倾角和偏角,μ0为真空磁导率.
Mq为偶极源的磁矩,I和D分别是偶极源的总磁化方向倾角和偏角,μ0为真空磁导率.定义第q点磁偶极源在测区上的理论磁总场异常ΔTq与实测磁总场异常ΔT的互相关系数为
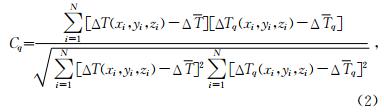
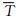 是实测磁总场异常的平均值,Δ
是实测磁总场异常的平均值,Δ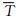 q是第q点偶极源的理论磁总场异常的平均值.
q是第q点偶极源的理论磁总场异常的平均值.假设Mq>0,则将公式(1)代入公式(2)可得
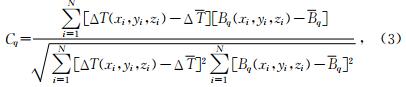
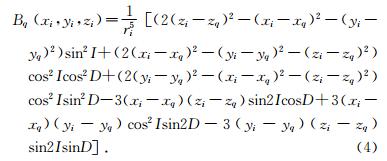
根据公式(3)和(4)计算地下坐标(xq,yq,zq)、总磁化方向倾角I、偏角D的偶极源理论磁总场异常与实测磁总场异常的互相关系数.若Cq越大,说明x、y、z、I、D五个参数值越接近真实值,反之亦然.根据异常特性,对五个参数的每个参数选取一定范围,并以一定的步长递变,依据公式(3)和(4)计算相应的相关系数值,相关系数最大值表明其所对应的五个参数与真实值最接近.于是,取相关系数最大值对应的总磁化方向倾角和偏角作为最终估计出的磁化方向倾角和偏角.
2 理论模型数据试验
理论模型由四个大小不同、受不同斜磁化的长方体组合而成,表 1列出了各长方体几何参数和磁化方向.已知各长方体的磁化强度均为10 A/m,正演计算该模型在高度为0 m的水平观测面上的理论磁总场异常,并引入基准值4%的高斯随机噪声,图 1显示了该模型的含噪磁总场异常,其中白色方框1、2、3和4为各长方体实际水平位置分布.
|
|
表 1 理论模型各长方体几何参数和磁化方向 Table 1 The geometric parameters and magnetization direction of each prism in synthetic model |
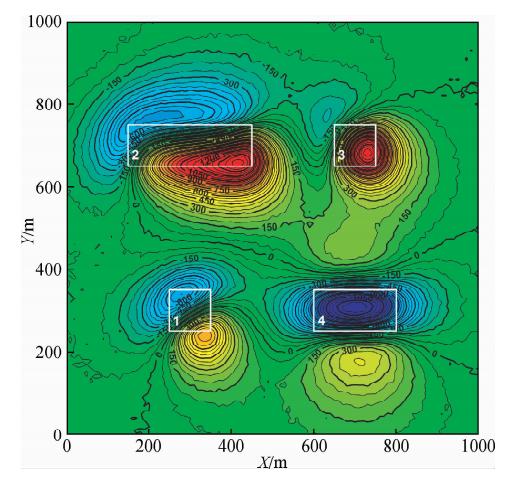 | 图 1 理论模型的含噪斜磁化磁总场异常,单位为nT Fig. 1 The noisy magnetic total field anomalies of synthetic model,the unit is nT |
下面利用本文的偶极源互相关法对理论含噪斜磁化磁总场异常进行磁化方向估计试验,实际磁化方向如图 2中黑色实线箭头所示.首先,根据异常特征划分出四个分块A、B、C和D(图 2中白色方框),每个分块包含一个孤立磁异常.然后,分别选取四个分块试验所用的偶极源空间范围和步长:坐标x范围为全区、步长为50 m;坐标y范围为全区、步长为50 m;坐标z范围为50 m~300 m、步长为50 m.选取分块A、B和C的总磁化方向倾角I范围为20°~90°、步长为1°,偏角D范围为-90°~90°、步长为1°;选取分块D的总磁化方向倾角I范围为-40°~40°、步长为1°,偏角D范围为-40°~40°、步长为1°.利用公式(3)和(4)分别计算各分块互相关系数,得到每个分块的相关系数最大值所对应的偶极源磁化方向,如表 2和图 2白色粗虚线箭头所示.
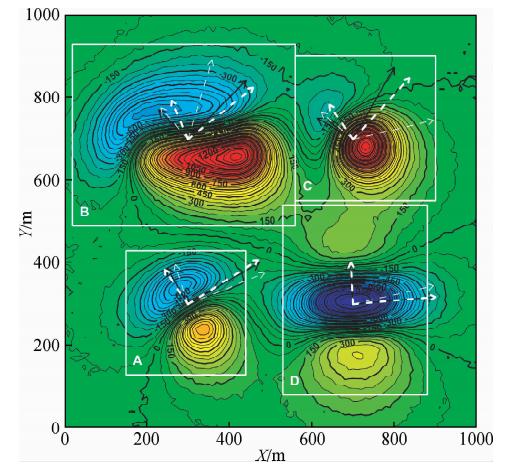 | 图 2 偶极源互相关法和Dannemiller互相关 法估算总磁化方向,单位为nT Fig. 2 The estimated magnetization directions by the CMD method and Dannemiller’s method,respectively. The unit of magnetic anomaly is nT |
为进一步对比试验,本文利用Dannemiller互相关法对上述理论模型的含噪斜磁化磁总场异常进行了同样的估计试验,估算出的各分块总磁化方向(图 2中白色细虚线箭头).由于分块D中异常磁化方向近水平,应用Dannemiller 互相关法时还采用了低纬度地区的改进伪倾角化极方法(Macleod et al., 1993;石磊等,2012)对含噪磁总场异常进行化极处理.
图 2中黑色实线箭头为真实总磁化方向,白色粗虚线箭头为偶极源互相关法估计出总磁化方向,白色细虚线箭头为Dannemiller互相关法估算得到的总磁化方向.由图 2和表 2可以清楚地看出,偶极源互相关法能有效估算出总磁化方向,整体结果优于Dannemiller互相关法.在分块A和D中,对比Dannemiller互相关法结果,偶极源互相关法估算的总磁化方向倾角和偏角更接近于真实值.在分块B和C中,由于区块B和D部分异常的叠加,偶极源互相关法估计出的总磁化方向产生较小误差,而对叠加异常比较敏感的Dannemiller互相关法则产生较大误差.
|
|
表 2 偶极源互相关法和Dannemille互相关法 估算总磁化方向 Table 2 The estimated magnetization directions by the CMD method and Dannemiller’s method |
中国西北某金属矿区矿床形成于晚古生代—早中生代(晚华力西—印支期)裂解及造山作用,矿床类型为矽卡岩型.矿体产于印支期中酸性侵入岩与石炭系灰岩接触带,岩体呈岩株状、岩枝状沿层间构造和层节理侵入于石炭系上统灰岩地层中.矿区磁铁矿为强磁性,磁化率均值在80000×10-5 SI以上,具有明显剩磁.矿区灰岩基本无磁性,中酸性花岗闪长岩表现为一般的磁性,磁化率范围为62×10-5 ~4068×10-5 SI,接触带附近矿化后的矽卡岩类表现为强磁性,磁化率变化范围为10000×10-5~100000×10-5 SI.
勘探区某异常点的航磁异常数据网格为64×49,网格点间距为150 m,观测面较平坦,平均飞行高程约3600 m.图 3显示为该异常点的航磁异常,异常幅度在-54~65 nT.航磁异常主体由两个大小近似相等的近等轴状异常组成,已知勘探区现代地磁场方向倾角为56.25°,偏角为0.57°.
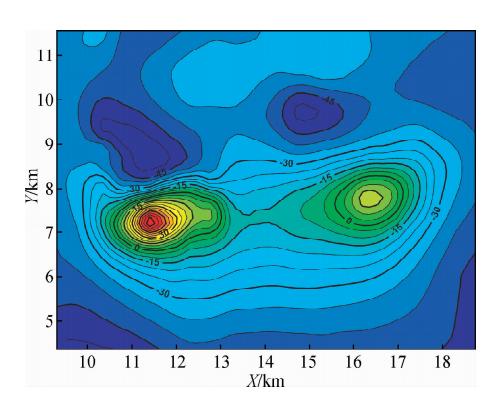 | 图 3 矿区某异常点实际航磁异常,单位为nT Fig. 3 The real aeromagnetic anomalies from a metallic deposit area in northwestern China, the unit is nT |
下面利用本文的偶极源互相关法对某异常点的航磁异常进行总磁化方向估计试验.首先,根据异常特征对数据划分出两个分块(图 4中白色方框A和B),每个分块包含一个孤立磁异常.然后,使用偶极源互相关法独立估计每块数据的总磁化方向.根据异常特征,选取试验所用的偶极源五个参数范围和步长如下:坐标x范围为全区,步长150 m;坐标y范围为全区,步长150 m;坐标z范围为600~3000 m,步长200 m;总磁化方向倾角I范围为10°~80°,步长为1°;偏角D范围为-90°~0°,步长为1°.最后,利用公式(3)和(4)计算各分块互相关系数最大值,经计算得到A分块总磁化方向倾角I=38°,偏角D=-9°(图 4中白色实线箭头);B分块总磁化方向倾角I=33°,偏角D=-11°,见图 4中白色实线箭头.由图可见,偶极源互相关法估计得到的总磁化方向与现代地磁场方向(I=56.25° and D=0.57°)存在差异,这是由于剩磁的存在使现代地磁场方向与总磁化方向不同.
本文同样使用了Dannemiller互相关法对实际航磁数据进行试验,得到A分块总磁化方向倾角I=22°,偏角D=50°(图 4中白色虚线箭头);B分块总磁化方向倾角I=-15°,偏角D=44°,见图 4中白色虚线箭头显示.通过对比分析我们可以看出,Dannemiller方法估计得到的总磁化方向与现代地磁场方向和偶极源互相关法估算结果均有较大差异.
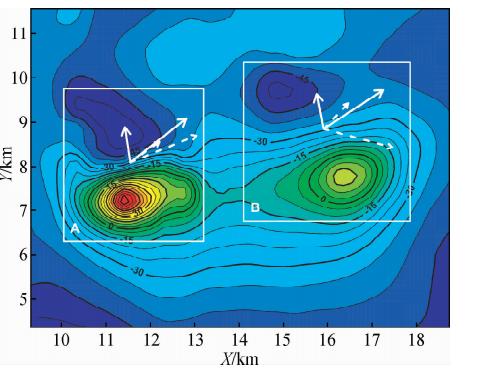 | 图 4 实际航磁异常采用不同方法估算出总磁化方向 Fig. 4 The estimated magnetization directions of real aeromagnetic anomalies by the CMD method and Dannemiller’s method,respectively. The unit of magnetic anomaly is nT |
偶极源互相关法估算出的A、B两个分块总磁化方向比较接近,因此我们采用它们的平均值作为研究区总磁化方向,即倾角I=35.5°,偏角D=-10°,并以此磁化方向对实际航磁异常做化极处理.图 5显示了化极后研究区磁异常,其主要反映两个近等轴状正值异常,异常明显向北移动,幅值变化范围为-73~89 nT.
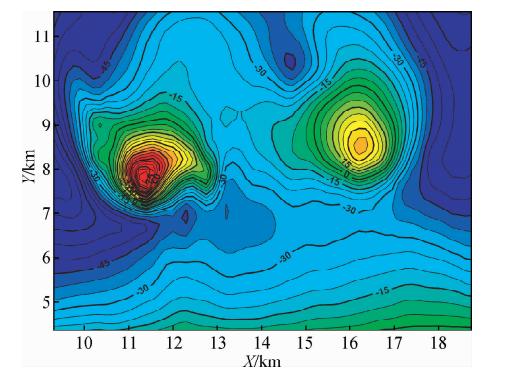 | 图 5 矿区某异常点实际航磁异常化极异常,单位为nT Fig. 5 The RTP anomalies in research area using estimated magnetization direction by the CMD method,the unit is nT |
本文研究提出估计磁总场异常磁化方向的偶极源互相关法,即用磁偶极源的理论磁总场异常与实测磁总场异常作互相关,用一系列递变的偶极源位置和总磁化方向做试错,取互相关最大化对应的总磁化方向作为估计结果.理论模型和实际航磁数据试验表明本方法可靠、有效.
偶极源互相关法简单易行,避免常规估计方法必需的异常分量换算、化磁极、求导或磁源重力异常换算等处理及其间接引入的误差.对于低纬度地区,不存在化极等处理的不稳定性和误差问题,抗干扰能力强;对平面或起伏观测面、规则或不规则磁测数据都能适用.理论数据和实际航磁数据试验表明偶极源互相关法能从近等轴状磁总场异常中有效估计出总磁化方向.
| [1] | Dannemiller N, Li Y G. 2006. A new method for determination of magnetization direction[J]. Geophysics, 71(6): L69-L73. |
| [2] | Gan X. 2001. Feasibility of the application of microcomputer method to the magnetic direction determination of the magnetic body[J]. Hubei Geology & Mineral Resources (in Chinese), 15(1): 33-38. |
| [3] | Gerovska D, Arauzo-Bravo M J, Stavrev P. 2009. Estimating the magnetization direction of sources from southeast Bulgaria through correlation between reduced-to-the-pole and total magnitude anomalies[J]. Geophysical Prospecting, 57(4): 491-505. |
| [4] | Guo L H, Meng X H, Shi L. 2011a. 3D correlation imaging of the vertical gradient of gravity date[J]. Journal of Geophysics and Engineering, 8(1): 6-12. |
| [5] | Guo L H, Shi L, Meng X H. 2011b. 3D correlation imaging of magnetic total field anomaly and its vertical gradient[J]. Journal of Geophysics and Engineering, 8(2): 287-293. |
| [6] | Guo L H, Meng X H, Shi L. 2012. Global correlation imaging of magnetic total field gradients[J]. Journal of Geophysics and Engineering, 9(5): 508-515. |
| [7] | Helbig K. 1963. Some integrals of magnetic anomalies and their relationship to the parameters of the disturbing body[J]. Zeitschrift für Geophysik, 29(2): 83-96. |
| [8] | Macleod I N, Jones K, Dai T F. 1993. 3-D analytic signal in the interpretation of total magnetic field data at low magnetic latitudes[J]. Exploration Geophysics, 24(4): 679-688. |
| [9] | Medeiros W E, Silva J B C. 1995. Simultaneous estimation of total magnetization direction and 3-D spatial orientation[J]. Geophysics, 60(5): 1365-1377. |
| [10] | Phillips J D. 2005. Can we estimate total magnetization directions from aeromagnetic data using Helbig's integrals[J]. Earth, Planets, and Space, 57: 681-689. |
| [11] | Roest W R, Pilkington M. 1993. Identifying remanent magnetization effects in magnetic data[J]. Geophysics, 58(5): 653-659. |
| [12] | Shi L, Guo L H, Meng X H, et al. 2012. The modified pseudo inclination method for magnetic reduction to the pole at low latitudes[J]. Chinese Journal of Geophysics (in Chinese), 55(5): 1775-1783, doi:10.6038/j.issn.0001-5733.2012.05.035. |
| [13] | Tang J D. 1986. Determination of the directions of magnetizations for an arbitrary body[J]. Journal of Guilin College of Geology (in Chinese), 6(2): 169-175. |
| [14] | 甘西. 2001. 利用微机确定磁性体磁化方向的可行性探讨[J]. 湖北地矿, 15(1): 33-38. |
| [15] | 石磊, 郭良辉, 孟小红,等. 2012. 低纬度磁异常化极的伪倾角方法改进[J]. 地球物理学报, 55(5): 1775-1783, doi:10.6038/j.issn.0001-5733.2012.05. 035. |
| [16] | 唐俊德. 1986. 任意磁性体磁化强度方向的确定[J]. 桂林冶金地质学院学报, 6(2): 169-175. |
 2014, Vol. 29
2014, Vol. 29

