2. 石油数据挖掘北京市重点实验室(Z121109009212008), 北京 102200
2. Beijing Key Laboratory of Oil and Gas Data Mining(Z121109009212008), Beijing 102200, China
0 引 言
波场数值模拟是人们理解波在不同介质中传播规律,认识和正确理解采集波信号的携带重要信息的重要手段(魏修成等,1998).但是由于时间域内粘弹性介质的本构方程是一种卷积积分形式,无法将它直接离散化数值求解.围绕这一问题,国内外许多学者提出了多种粘弹性介质的数值模拟方法.Day等(1984)首次将Pade近似方法应用于粘弹性介质数值模拟当中,并利用交错网格有限差分方法模拟常Q粘弹性介质中二维地震波场.随后,Emmerich等(1987)提出一种计算效率更高的近似方法,他们根据流变学的“广义标准线性体”(generalized st and ard linear solid,简称GSLS模型),来逼近介质的粘弹性;并利用该方法与Dey等方法进行对比,证明在相同阶数的情况下精度得到较大的提高.Kristek等(2003)应用Emmerich等人的方法,应用于常Q粘弹性介质地震波模拟中,同时修改粘弹性函数,从而减小了方程的数目.张智(2005)利用伪谱法,用伪谱法研究了在常Q粘弹介质地震波场模拟中的应用效果.
谐振Q模型综合考虑了地震波在固体和流体中的能量损耗,能够较全面的描述地层的粘弹性特征(杨文采,1987).本文采用GSLS模型逼近谐振Q模型的粘弹性,通过引入新的P波波场变量及S波波场变量,推导了粘弹性介质中实现P波和S波分解的等价方程,同时将完全匹配吸收边界(PML)条件引入到谐振Q模型介质的数值模拟中.最后利 用交错网格高阶有限差分法求解等价方程,分别研究了纵、横波在谐振Q模型介质中波的振幅衰减及相速度的频散等特征.
1 GSLS模型逼近粘弹性的推导
频率域内各向同性粘弹性介质的本构方程为

用于逼近粘弹性的GSLS模型为
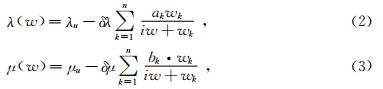
式中,λu、μu,为非松弛模量,wj为地震波主频附近的n个特征频率值,ak、bk、δλ、δμ为待定系数,且有

将方程(2)、(3)代入(1)式中,并对两端进行傅里叶逆变换,可以得到方程
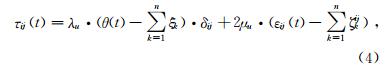
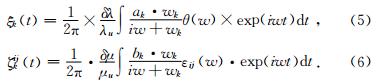
对方程(5)、(6)两端求时间导数,可以得到
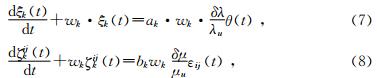
方程系数ak及bk值主要通过频率域GSLS模型逼近给定的谐振Q模型介质的Q值和复弹性模量而得到.具体方法为,在松弛频率范围内选取2n-1个频率wh,在给定的介质中,根据谐振Q模型公式可以得到频率wh所对应的Q值及复弹性模量实部;根据最小二乘方法利用方程(2)、(3)逼近这些理论计算的Q值及复弹性模量实部值,进而得到方程(2)、(3)中的系数ak及bk值.将他们带入方程(4)、(7)、(8)中,得到时间域粘弹性介质的本构方程.
2 纵横波分解等价方程及其差分格式
在弹性波动力学理论中,通常用标量位的梯度和向量位的旋度之和表达弹性波波场的P波和S波分解,以此来进行数值模拟是不太方便的.通过引入P波波场变量及S波波场变量,可以得到P波和S波分解的等价方程(马德堂等,2003).将该方法引入粘弹性介质中,可以得到分离的纯P波或纯S波波场,并保留了P波和S波相互转换的信息.
2.1 纵横波分解等价方程
由二维各项同性粘弹性介质本构关系,同时引入P波速度变量、S波速度变量及应力变量,给出粘弹性介质的速度—应力方程的等价方程, 动量方程为

应力与应变一阶导的关系可表示为

其中,λu、μu,为非松弛模量,ξkkh,ζλkkh,ζμxzh粘弹性项一阶时间导数.
粘弹性项方程为

2.2 等价方程差分格式
运用交错网格有限差分技术,求解粘弹性介质的速度—应力方程的等价方程.图 1给出了各波场变量及地层介质参数在二维交错网格中的相对位置.图中,(i,j)代表空间网格坐标.
 | 图 1 二维交错网格单元示意图 Fig. 1 Stencil of discretization scheme in staggered grid scheme in 2D |
在交错网格技术中,变量的导数是在相应的变量网格点之间的半程上计算的,波场中的变量f(x,y)为例,它的空间x方向一阶导数的2N阶精度差分近似式可写为

李振春等(2007)给出了时间精度为2阶、空间为2N阶精度的有限差分法稳定性条件为

2.4 震源激发方式
通过引入P波波场变量及S波波场变量,可以得到P波和S波分解的等价方程(马德堂、朱光明,2003).将该方法引入粘弹性介质中,可以得到分离的纯P波或纯S波波场,并保留了P波和S波相互转换的信息.
3 PML吸收边界条件
根据PML吸收边界条件的基本原理(严红勇等,2012),采用时间域变量分裂的方法,对粘弹性介质中一阶速度—应力等价方程进行变量分裂,可以得到应用于粘弹性介质中等价方程的PML吸收边界条件公式.对于(18)、(19)式,每一个波场变量分为两部分,而(17)式引入的P波速度变量、S波速度变量正好对应着U、V的分裂的形式,以应力变量为例,有

式中的上标末尾的x和z代表该项与相应空间导数有关的标示.同时,可以得到分裂后的PML吸收边界中带有衰减因子的波动方程.方程(22)吸收边界方程的具体形式为


式中qx,qz代表x,z方向的衰减因子,边界的不同区域,它们的取值不同;上下区间qx=0,qz>0;左右区间qx>0,qz=0;四个角区域qx>0,qz>0.
依据(20)形式,对方程(24)、(25)的空间导数2M阶精度离散化得到

4 数值模拟过程
4.1 GSLS模型可靠性验证
本次模拟主要是利用GSLS模型逼近谐振Q模型,通过对比频率域谐振Q模型计算的品质因子Q(w)及复模量的实部MR(w)与逼近的GSLS模型模拟结果,以验证GSLS模型的可靠性.实验的松弛频率范围选在10到103 Hz之间,介质参数如表 1所示.图 2和3为模拟的单层谐振Q模型介质.
|
|
表 1 层谐振Q模型介质参数 Table 1 The value of single layer’s parameters in the resonance Q media |
GSLS模型近似阶数为n=10时,拟合的纵、横波的品质因子Q值及复模量实部与理论计算的值进行对比如图 1和图 2所示.
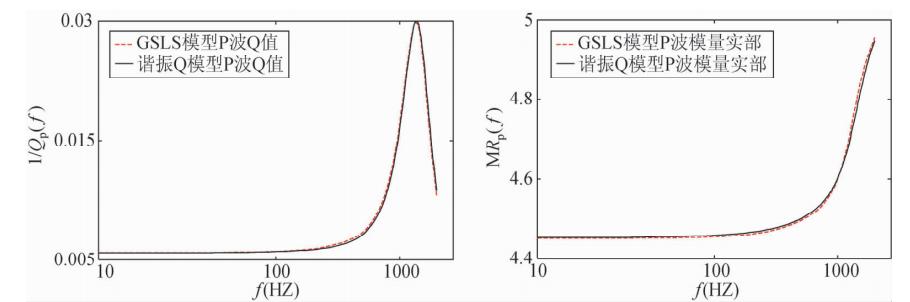 | 图 2 谐振Q模型计算得到的纵波Q值及复模量实部值与拟合的GSLS模型计算得到的结果对比 Fig. 2 The contrast between the Q value and the real part of the modulus of the P-wave calculated by resonance Q model and the one the by GSLS model |
通过对比谐振Q模型计算结果与拟合结果,可以看出10阶GSLS模型能够很好的逼近谐振Q模型.
4.2 PML吸收效果及纵横波分解效果
为检验PML吸收效果及纵横波分解效果.采用不同的震源激发方式,分别在单层及双层谐振Q模型介质中进行,分别检验了PML吸收效果、纵横波分解效果.
4.2.1 PML吸收效果检验
为验证谐振Q模型介质中PML吸收效果,设计一个大小为250×250个网格的二维单层介质,吸收边界厚为50个网格.空间采样间隔Δx=Δz=3.4 m,时间步长Δt=1 ms,震源采用主频为30 Hz的雷克子波,震源位置设置于网格坐标(125、125)处.震源激发方式采用集中力源方式,同时产生纵、横波波场.谐振Q模型参数如表 1所示,吸收系数为0.2.图 4a和b为分别考虑PML吸收边界时得到的x、z两个分量的波场快照,分别对应着150 ms、200 ms、250 ms、350 ms时的波场快照.
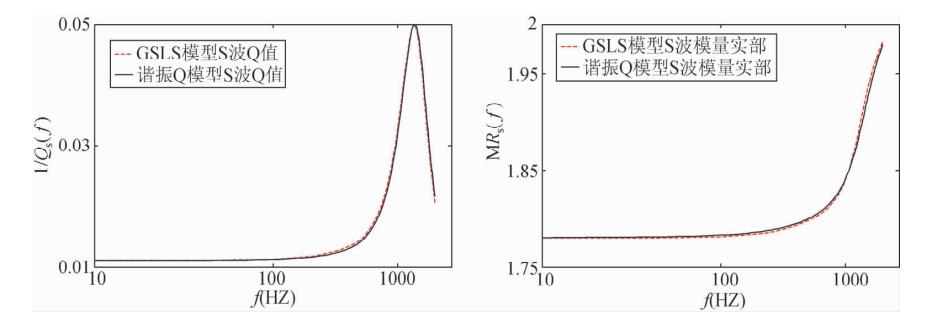 | 图 3 谐振Q模型计算得到的横波Q值及复模量实部值与拟合的GSLS模型计算得到的结果对比 Fig. 3 The contrast between the Q value and the real part of the modulus of the S-wave calculated by resonance Q model and the one by the GSLS model |
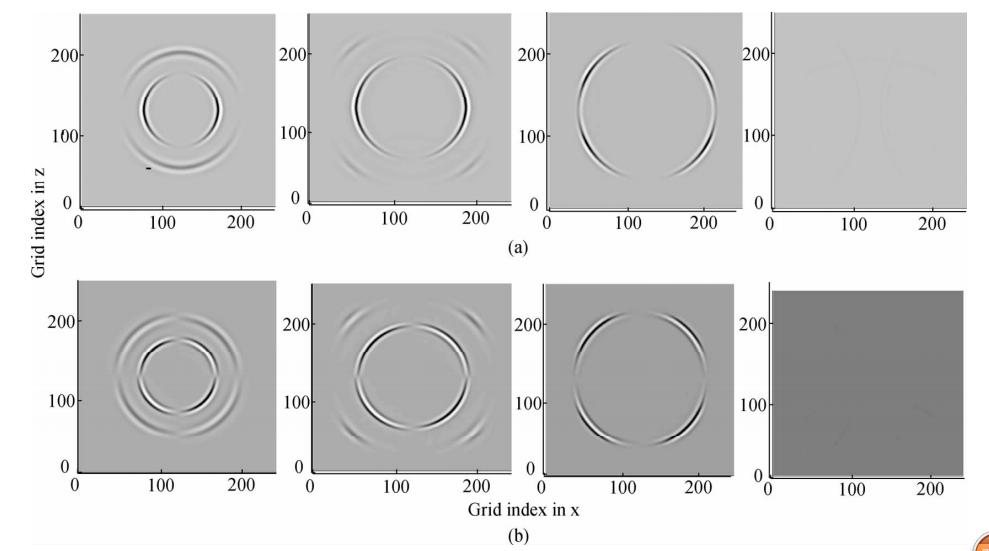 | 图 4 单层介质中波场的PML吸收效果快照 (a)为x分量;(b)为Z分量. Fig. 4 The snapshot of wakefield in the resonance Q media with PML absorption effect (a)The x-component’s and (b)The z-component’s. |
吸收效果如图 3所示,PML吸收边界对纵横波都有良好的吸收效果.
4.2.2 纵、横波分解效果
为检验谐振Q模型介质中的纵横波分解效果,分别采用不同震源,进行三次模拟.
第一次模拟在单层介质(参数如表 1)中,设计一个大小为250×250个网格的二维介质,吸收边界厚为50个网格. 空间采样间隔Δx=Δz=3.8 m,时间步长Δt=1 ms,震源采用主频为30 Hz的雷克子波,震源位置设置于网格坐标(125,125)处.震源激发方式采用集中力源方式,沿Z轴激发,产生混合波qPS及分解的纯纵波qP和纯横波qS.图 5a和b分别为x、z分量,t=200 ms时的混合粘弹性波混合场及分离后的纯P波与纯S波波场快照.
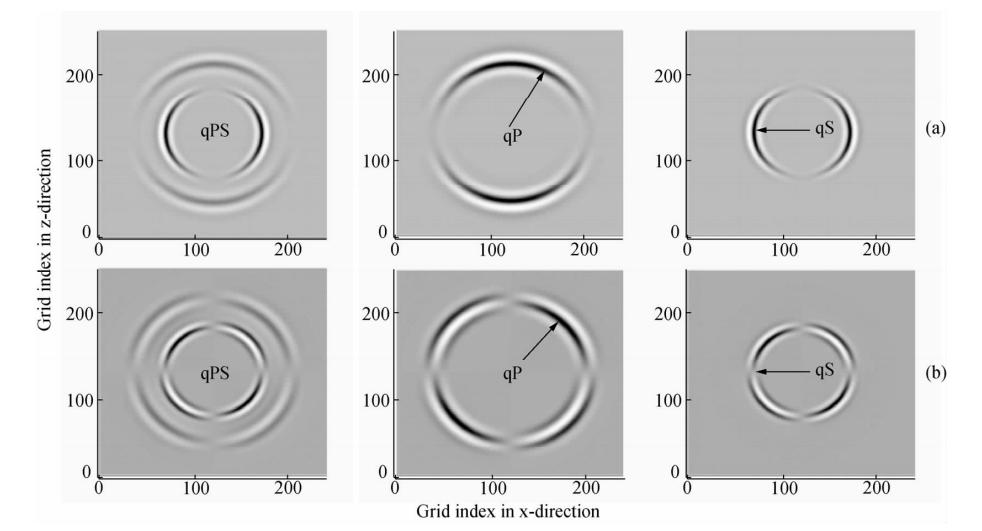 | 图 5 单层介质纵横波分解 (a)x分量纵、横波分量快照;(b)z分量纵、横波分量快照. Fig. 5 Snapshot of wakefield in the resonance Q media about the P-wave and S-wave decomposition (a)The x-component’s;(b)The z-component’s. |
|
|
表 2 双层介质谐振Q模型参数 Table 2 The vale of two layers’ parameters in the resonance Q media |
第二次模拟在双层介质中进行,介质参数如表 2所示.设计一个大小为250×250个网格的二维介质,吸收边界厚为50个网格.双层介质的反射界面水平,位于网格坐标z=80处,为满足稳定性条件(式25),空间采样间隔ΔX=ΔZ=3.8 m,时间步长Δt=1 ms.震源采用主频为30 Hz的雷克子波,震源位置设置于网格坐标(125,125)处.波源激发方式采用纯P波源激发,只产生P波.图 6a和b为x、z分量t=200 ms波场快照.
 | 图 6 双层介质纵波波源的波场分解快照 (a)x分量纵、横波分量快照;(b)z分量纵、横波分量快照. Fig. 6 The snapshot of Wakefield in the resonance Q media about the P-wave and S-wave decomposition arousing by P-wave source (a)The x-component’s;(b)The z-component’s. |
反射界面处除了产生反射P波(RqP)与透射P波(TqP)外,在反射界面处还有微弱反射的转换S波(RqS)及透射的转换S波(TqS)(如图 5所示).
第三次模拟,除震源激发方式不同外,其他设置都相同.震源采用了纯S波源激发,只产生S波.图 7(a、b)为x、z分量t=200 ms波场快照.
反射界面处除了反射S波(RqS)与透射的S波(TqS)外,还有微弱反射的转换波(RqP)及透射的转换波(TqP)(如图 7所示).
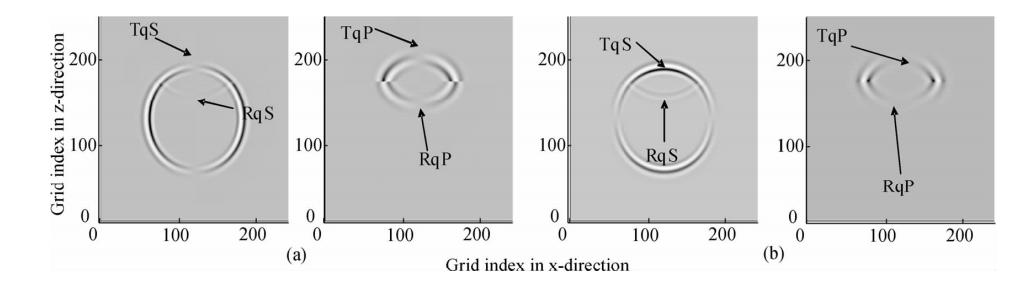 | 图 7 双层介质横波波源的波场分解快照 (a)为z分量纵、横波分量快照;(b)为x分量纵、横波分量快照. Fig. 7 The snapshot of wakefield in the resonance Q media about the P-wave and S-wave decomposition arousing by S-wave source (a)The x-component’s;(b)The z-component’s. |
通过数值模拟,分别模拟谐振Q模型介质中的能量吸收及速度频散特征.
4.3.1 粘弹性介质中波幅值衰减
为研究P、S波在谐振Q模型介质中的振幅衰减特征,设计三个大小相同,都为为400×600个网格的二维单层介质,介质参数如表 3所示.震源位于网格坐标(200,400)处,采用沿Z轴的集中力源激发方式,震源函数为雷克子波,主频fm=25 Hz,记录点设为(200,50)处.
|
|
表 3 三种粘弹性介质所对应的参数 Table 3 The parameters about the 3 kinds of resonance Q medias |
图 8和9分别为记录点接收到的纵(qp)、横(qs)波x、z分量的地震记录.图 8和9中纵、横波随着Q值的减小,衰减越严重,且横波更为明显.
 | 图 8 在记录点处记录的不同介质模型中纵、横波x分量 Fig. 8 The contrast of the records about the x-components of the P-wave and the S-wave in the different resonance Q medias |
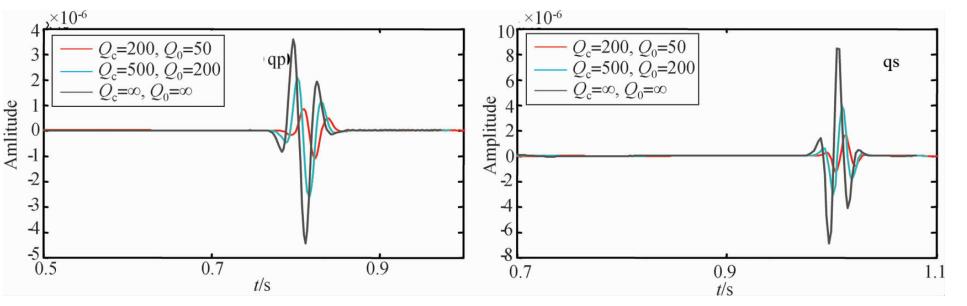 | 图 9 在记录点处记录的不同介质模型中纵、横波z分量 Fig. 9 The contrast of the records about the z-components of the P-wave and the S-wave in the different resonance Q medias |
本次研究设计两个深度不同的震源,通过对比两个震源所激发的不同主频地震波到达记同一录点的时间间隔及振幅的差异,来研究谐振Q模型介质中的速度及振幅随频率变化的特征. 模拟设计两个单层二维介质的网格,大小分别为300×500和300×800,震源分别处于(150,350)及(150,650)处,震源的激发方式都为集中力源,记录点为(150,50).震源主频分别为20、30、40 Hz.两套网格的谐振Q模型参数相同如表 1.
 | 图 10 不同主频及位置的震源激发得到的纵、横波z分量记录 (a)、(c)为震源位于(150,350)时地面得到的纵、横波Z轴方向地震记录; (b)、(d)为震源位于(150,650)时地面得到的纵、横波Z轴方向地面记录. Fig. 10 The contrast of the z-components records of the P-wave and S-wave aroused by sources with different dominant frequency and different sites (a)、(c)are the records aroused by source in(150,350)with different dominant frequency, (b)、(d)are the record aroused by the source in(150,650). |
 | 图 11 不同主频及位置的震源激发得到的纵、横波x分量记录 (a)、(c)为震源位于(150,350)时地面得到的纵、横波Z轴方向地震记录; (b)、(d)为震源位于(150,650)时地面得到的纵、横波Z轴方向地面记录. Fig. 11 The contrast of the x-components records of the P-wave and S-wave aroused by sources with different dominant frequency and different sites (a)、(c)are the records aroused by source in(150,350)with different dominant frequency, (b)、(d)are the record aroused by the source in(150,650). |
图 10和11中分别为在记录点处记录的x、z分量的纵(qp)、横(qs)波记录.通过图 10、11中,左右两边记录对比可知:由于粘弹性介质中地震波相速度速存在频散,且频率越高速度越快.因此随着地震波的传播,高频成分更早到达记录点.
5 结 论
5.1 只要近似阶数n值足够大,GSLS模型可以高精度的逼近谐振Q模型介质.
5.2 通过引入新的变量,给出了粘弹性介质波动方程的一种等价形式;用交错网格有限差分方法计算该波动方程,在不增加方程数目的情况下得到混合波场的同时,也得到了完全分离的纯P波或纯S波波场,并保留了P波和S波能量相互转换的信息.
5.3 通过对不同Q值及不同主频震源子波的波场进行模拟,可以看出不论P波还是S波,在谐振Q模型介质中,地震波在传播过程中存在明显的幅度衰减及相速度频散,并且横波比纵波更为明显.
| [1] | Chen K Y. 2012. Numerical modeling of pure seismic source in high precision [J]. Lithologic Reservoirs (in Chinese), 24(1): 84-91. |
| [2] | Day S M, Minster J B. 1984. Numerical simulation of attenuated wavefields using a Pade approximant method [J]. Geophysics, 78(1): 105-118. |
| [3] | Dong L G, Ma Z T, Cao J Z, et al. 2000. A staggered-grid high-order difference method of one-order elastic wave equation [J]. Chinese Journal of Geophysics (in Chinese), 43(3): 411-419. |
| [4] | Emmerich H, Korn M. 1987. Incorporation of attenuation into time-domain computations of seismic wave fields [J]. Geophysics, 52(9): 1252-1264. |
| [5] | Graves R W. 1996. Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences [J]. Bulletin of the Seismological of America, 86(4): 1091-1106. |
| [6] | Kristek J, Mcozo P. 2003. Seismic-wave propagation in viscoelastic media with material discontinuities: A 3D fourth-order staggered-grid finite-difference modeling [J]. Bulletin of the Seismological Society of America, 93(5): 2273-2280. |
| [7] | Lambert M A, Saenger E H, Quintal B, et al. 2013. Schmalholz. Numerical simulation of ambient seismic wavefield modification caused by pore-fluid effects in an oil reservoir [J]. Geophysics, 78(1): T41-T52. |
| [8] | Li Z C, Zhang H, Liu Q M, et al. 2007. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm [J]. Oil Geophysical Prospecting (in Chinese), 42(5): 500-515. |
| [9] | Ma D T, Zhu G M. 2003. Numerical modeling of P-wave and S-wave separation in elastic wavefield [J]. Oil Geophysical Prospecting (in Chinese), 38(5): 482-486. |
| [10] | Wei X C, Dong M Y, Chen Y T. 1998. Elastic wave propagation in inhomogeneous and anisotropic media [J]. Acta Seismologica Sinica (in Chinese), 20(6): 561-572. |
| [11] | Yan H Y, Liu Y. 2012. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics (in Chinese), 55(4): 1354-1365. |
| [12] | Yang W C. 1987. A resonance Q model for Viscoelastic rocks[J]. Chinese Journal of Geophysics (in Chinese), 30(4): 399-411. |
| [13] | Zhang Z, Liu C, Shao Z G, et al. 2005. The application of pseudo-spectral forward modeling of seismic wave field in constant Q viscoelastic medium [J]. Progress in Geophysics (in Chinese), 20(4): 945-949. |
| [14] | 陈可洋. 2012. 高精度地震纯波震源数值模拟[J]. 岩性油气藏, 24(1): 84-91. |
| [15] | 董良国, 马在田, 曹景忠,等. 2000. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 43(3): 411-419. |
| [16] | 李振春, 张华, 刘庆敏,等. 2007. 弹性波交错网格高阶有限差分法波场分离数值模拟[J]. 石油地球物理勘探, 42(5): 500-515. |
| [17] | 马德堂, 朱光明. 2003. 弹性波波场P波和S波分解的数值模拟[J]. 石油地球物理勘探, 38(5): 482-486. |
| [18] | 魏修成, 董敏煜, 陈运泰. 1998. 非均匀各向异性介质中弹性波的传播[J]. 地震学报, 20(6): 561-572. |
| [19] | 严红勇, 刘洋. 2012.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 55(4): 1354-1365. |
| [20] | 杨文采. 1987. 岩石的粘弹性谐振Q模型[J]. 地球物理学报, 30(4): 399-411. |
| [21] | 张智, 刘财, 邵志刚,等. 2005. 伪谱法在常Q粘弹介质地震波场模拟中的应用效果[J]. 地球物理学进展, 20(4): 945-949. |
 2014, Vol. 29
2014, Vol. 29

