在瞬变电磁正演过程中，首先计算频率域层状介质的电磁响应，经过频-时转换，得到电磁场的时间域响应.频-时转换有多种方法，傅里叶变换(Newman，1986；陈向斌，2008)，Guptasarma算法(Guptasarma，1982；阮百尧，1996)，G-S逆拉式变换方法(Knight，1982；朴化荣， 1987，1990；罗延钟，2000；李永兴，2010；李建慧， 2011，2013)，线性数字滤波法(Anderson，1979；刘继东，1996)和余弦变换法(殷长春，1994；昌彦君，1998；翁爱华，2010)等.每种方法有不用的使用范围和精度，如傅里叶变换具有很强的适用性，对各种发射源和地电模型都适用，但是计算量大且计算速度慢；G-S逆拉式变换方法计算速度比较慢，但是计算复杂地电模型较有优势；余弦变换法计算精度高，对于缓变函数计算效果非常好(薛国强，2008).昌彦君等(1995)基于电偶源的解析解，对G-S逆拉式变换、线性数字滤波和余弦变换方法做了比较，认为余弦变换的计算精度最高.余弦变换目前多采用折线逼近法或数字滤波法(考夫曼，1987；王华军，2004)来计算.但在前人的论述中，折现逼近法的积分步长难以控制，要采用误差控制步长(李建慧，2012).在我们实际应用的过程中发现，频率范围的选择也起到了决定性作用.在本文中，笔者基于折线逼近法，通过与解析解的对比，来讨论频率范围对余弦变换精度的影响，从而确定出在多种因素影响下最佳频率范围的选择，使瞬变响应计算精度达到最高.

1 瞬变响应计算

频率域和时间域瞬变电磁场之间的关系可以表示为

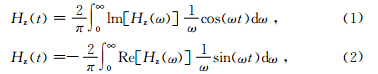
式中Re[Hz(ω)]，lm[Hz(ω)]分别为垂直磁场Hz频率域响应的实部和虚部，ω为角频率，t为时间.

利用折线逼近法来计算(1)和(2)式，对于一般的情况

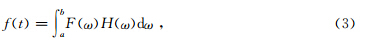
采用分布积分，用S_k代替 dF dω，最后重新写出其中各项，整理后可以得到关于f(t)的近似表达式ƒ_∧(t)

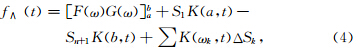
其中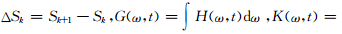

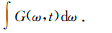
当H(ω，t)=cos(ωt)，a=0，b=+∞时整理得到Hz(t)的近似表达式H^{^}_z(t)为

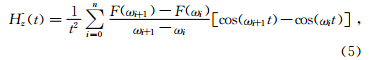
上式中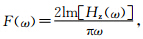公式(5)就是利用折线逼近方法计算余弦变换的基本公式(考夫曼，1987).从公式可见，为了获得较高的计算精度，需要选择适当的F(ω)和n，F(ω)是由频率区间决定的，因此选择合适的频带对计算精度起到关键性作用.

2 数值结果 2.1 频率区间设置

由于在模拟过程中，考虑到了位移电流，所以在讨论的过程中，我们把高频限设置为f^max_H=10⁸ Hz，低频限f^min_L=10^－8 Hz，选取对数频率宽度为12的5个频率区间，具体见表 1.在每个频率区间内，等对数间隔采集300个频点，计算出相应的频率域响应，均匀半空间大回线和磁偶极子的垂直磁场的频率域响应计算参见(考夫曼，1987)，再利用上述的余弦变换公式(5)，计算出相应的瞬变响应，并与解析解对比，确定出5个频率范围fⁱ_L~fⁱ_H(i=1，2，3，4，5)中平均百分比误差最小的那个频带B_i，然后，在此最佳频带的基础上分别：(1)固定ƒ_L，缩小和扩大ƒ_H；(2)固定ƒ_H，缩小和扩大ƒ_L；(3)同时缩小和扩大ƒ_L、ƒ_H，来进一步分析频带选择对余弦变换结果的影响，从而确定出最优的频率范围.

表 1(Table 1)

表 1 5个频带(单位Hz)分布 Table 1 Five frequency ranges B1 B2 B3 B4 B5 10－8~104 10－7~105 10－6~106 10－5~107 10-4~108

表 1 5个频带(单位Hz)分布 Table 1 Five frequency ranges

电阻率影响是利用大回线源解析解来讨论的.在电阻率分别为100 Ωm，500 Ωm的均匀半空间条件下，发射回线的半径为50 m.

图 1a和图 1b给出了电阻率100 Ωm时，表 1中5个频带(单位Hz)的频率响应，余弦变换与解析解对比情况，从图 1a可见，计算误差主要出现在瞬变响应的早期和晚期两端，特别是早期，误差受频带范围选择的影响更大.比较图 1b，不同频率范围，计算精度不同，频率范围B3的计算误差最小，频带向高频和低频移动，都将导致计算误差变大.因此必须选择合适的频率范围.事实上，当采用B1的频率范围，由于高频信息的相对缺失，导致早期瞬变信号的误差明显增加.而向高频移动，变为B5，早期误差明显减小，但晚期误差相对增加.因此，最佳频率范围的选择还应考虑观测时窗，对于本例，最佳的频率范围为10^－6~10⁶ Hz.在此频率范围的基础上，进一步改变，分别求出6个频率范围时间域响应，与解析解对比的平均百分比误差如表 2所示.从表中可以看出，当f_H>10⁶ Hz且log^f_H－log^f_L≥11时，计算精度都能得到保证.综合上述各个频率范围余弦变换结果可以发现，电阻率为100 Ωm的情况下，余弦变换的最佳频率选择范围可以选择为10^－6~10⁶ Hz.

图 1

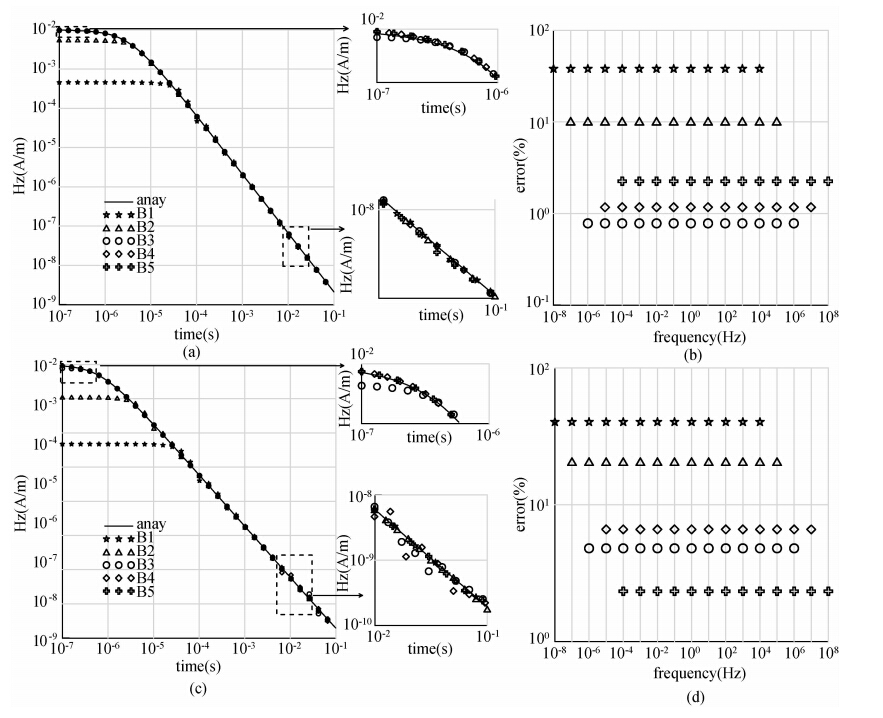图 1 均匀半空间，半径为50 m的地面大回线中心Hz的瞬变响应和百分比误差 (a)电阻率为100 Ωm；(b)百分比误差； (c)电阻率为500 Ωm；(d)百分比误差. Fig. 1 In homogeneous halfspace, the radius of 50 m ground large loop center Hz transient response and the percentage error

表 2(Table 2)

表 2 电阻率为100 Ωm时，不同频带响应误差 Table 2 Resistivity is 100 Ωm，the different frequency b and response error 频率范围(Hz) 10－6~105 10－6~107 10－7~106 10－5~106 10-5~105 10－7~107 平均误差 11.05% 1.33% 1.32% 1.25% 10.34% 1.41%

表 2 电阻率为100 Ωm时，不同频带响应误差 Table 2 Resistivity is 100 Ωm，the different frequency b and response error

电阻率为500 Ωm时，分别计算表 1中5个初始频段的时间域响应，如图 1c和图 1d所示，通过对比可以看出，最低频率大于10^-6 Hz时，计算的误差都能满足精度要求.这是由于介质电阻率增加，低频的感应效应弱，必须有更高频的信息参与响应计算.综合分析图 1c和图 1d，最佳的频带为10^－4~10⁸ Hz.为进一步分析频带的影响，又分别计算了6个频段的瞬变响应，与解析解对比的平均百分比误差如表 3所示.从表中可见，在电阻率增高后，只要高频端f_H>10⁷ Hz，频带宽度在12个数量级，余弦变换的精度都较高.

表 3(Table 3)

表 3 电阻率为500 Ωm时，不同频带响应误差 Table 3 Resistivity is 500 Ωm，the different frequency b and response error 频率范围(Hz) 10－4~107 10－4~109 10－5~108 10－3~108 10－5~109 10－3~107 平均误差 1.62% 2.21% 2.21% 1.64% 1.91% 1.88%

表 3 电阻率为500 Ωm时，不同频带响应误差 Table 3 Resistivity is 500 Ωm，the different frequency b and response error

比较图 1和表 2、3可见，在给定的时窗范围内，对于常用的大回线(半径为50 m)，余弦变换的计算精度主要取决f_H，只要f_H>10⁷ Hz，带宽在12个数量级，精度都能得到保证.从图 1对比可以见，随着电阻率的增大，余弦变换对频率区间的依赖增强.

2.3 线圈大小的影响

为了讨论线圈大小对余弦变换频率区间选择的影响，我们在图 1的基础上进一步计算了电阻率为100 Ωm的均匀半空间，线圈半径为50 m，1000 m的中心H_Z的TEM响应，具体结果如图 2和表 4所示.

表 4(Table 4)

表 4 回线半径为1000 m时，不同频带响应误差 Table 4 The loop radius is 1000 m，the different frequency b and response error 频率范围(Hz) 10－6~105 10－6~107 10－7~106 10－5~106 10－5~105 10－7~107 平均误差 0.14% 0.20% 0.20% 0.16% 0.11% 0.24%

表 4 回线半径为1000 m时，不同频带响应误差 Table 4 The loop radius is 1000 m，the different frequency b and response error

线圈半径为50 m、电阻率为100 Ωm的情况，在2.2中已经讨论过了，这里不再赘述.线圈半径为1000 m时，表 1中5个频段的瞬变响应及误差如图 2所示，改变频率范围f_H和f_L后的结果见表 4.从图 2和表 4可见，对于大回线源，如大定源发射，所有频率范围得到的晚期TEM精度都很高.从图 2b可见，计算误差主要是来自早期，并且同样取决于高频限，当f_H>10⁵ Hz时，精度都能满足.线圈半径为1000 m的 最佳频率范围为10^－5~10⁷ Hz.比较线圈半径为 50 m的情况可以看出，随着线圈半径的增加，频率范围的选取对余弦变换精度的影响减弱.

图 2

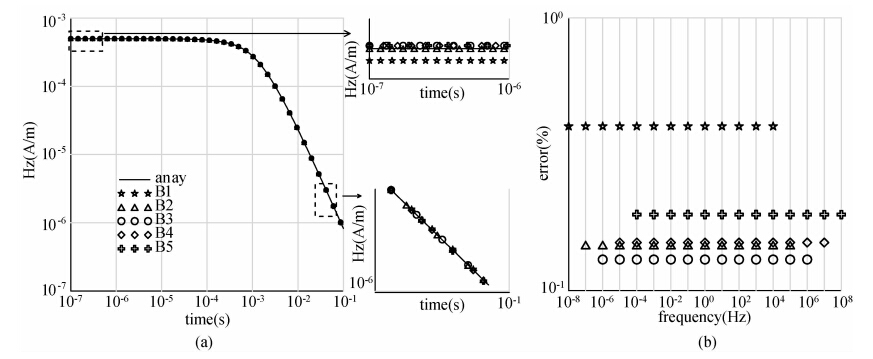图 2 电阻率为100 Ωm的均匀半空间，线圈半径为1000 m的地面大回线中心Hz的瞬变响应和百分比误差 (a)瞬变响应；(b)百分比误差. Fig. 2 The resistivity is 100 Ωm halfspace，radius is 1000 m large ground loop center Hz transient response and the percentage error

为了讨论收发距的影响，计算电阻率为100 Ωm的均匀半空间，地面垂直磁偶极子，收发距分别为500 m，1000 m时的TEM响应.频带取为表 1，结果如图 3所示.分别改变频率范围f_L和f_H后的误差统计见表 5和表 6.

图 3

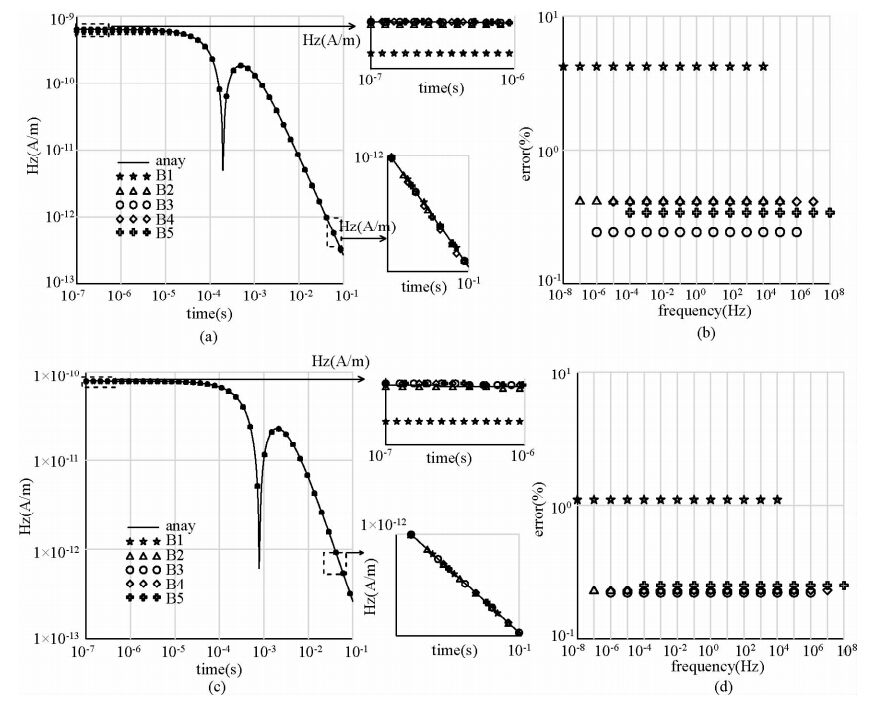图 3 电阻率为100 Ωm的均匀半空间，磁偶极子Hz的瞬变响应和百分比误差 (a)收发距为500 m；(b)百分比误差； (c)收发距为1000 m;(d)百分比误差. Fig. 3 The resistivity is 100Ωm halfspace，magnetic dipole Hz transient response and the percentage error

表 5(Table 5)

表 5 收发距为500 m时，不同频带响应误差 Table 5 The T-R distance is 500 m，the different frequency b and response error 频率范围(Hz) 10－6~105 10－6~107 10－7~106 10－5~106 10－5~105 10－7~107 平均误差 0.42% 0.37% 0.36% 0.29% 0.47% 0.56%

表 5 收发距为500 m时，不同频带响应误差 Table 5 The T-R distance is 500 m，the different frequency b and response error

表 6(Table 6)

表 6 收发距为1000 m时，不同频带响应误差 Table 6 The T-R distance is 1000 m，the different frequency b and response error 频率范围(Hz) 10－6~105 10－6~107 10－7~106 10－5~106 10－5~105 10－7~107 平均误差 0.20% 0.28% 0.28% 0.20% 0.17% 0.33%

表 6 收发距为1000 m时，不同频带响应误差 Table 6 The T-R distance is 1000 m，the different frequency b and response error

从图 3a、b可见，收发距为500 m时，除了10^－8~10⁴ Hz这个频带早期的效果不好，误差较大外，其他各个频带无论是在早期还是在晚期精度都很高.结合表 5，余弦变换的误差主要由低频限控制.当f_L>10^－6 Hz时，频率区间的选取对余弦变换的结果影响减弱，平均百分比误差基本在0.2%~0.3%浮动.因此，收发距为500 m时的最佳频率范围为10^－6~10⁶ Hz.

收发距离为1000 m时，表 1中5个频段的瞬变响应如图 3c、d所示.从图中可以看出，每个频率范围的余弦变换与解析解对比，整体来说，都有较高的精度.不过从局部的放大图来看，频带范围的选择只对早期TEM响应有影响，对中晚期TEM响应计算影响不大.并且，从图 3d所示，当低频高于10^-6 Hz时，计算误差都在5%以下.比较图 3b可见，随着收发距离的增加，为了得到较高的余弦变换计算精度，需要提供低频下限.或者说，更远处，需要更高频的信息，更低频响应计算误差变大，计算精度变差.

改变频率的结果如表 6可见，当f_L>10^－6 Hz，log^f_H－log^f_L≥12时，频率范围的选取对余弦变换的结果影响非常小，误差基本在0.2%~0.3%之间.因此，参考500 m的收发距，可以选择1000 m收发距离时的最佳频率范围为10^－6~10⁶ Hz，从表 5、表 6的对比可见，收发距增大，余弦变换的精度对频率区选取的依赖性减弱.

3 结 论

从上述的讨论可以看出，用折线逼近法计算余弦变换，其结果精度受到频率区间选择的影响.在固定折线数量，当电阻率不断增大时，频率区间的选择对计算结果的影响不断增强，f_H的选取对结果精度的贡献增强.当增大回线的半径时，频率区间的选取对计算结果的影响不断减弱，最佳的频率范围有减小的趋势.同样，当增大收发距时，频率区间的选取对计算结果的影响减弱，对最佳频率范围的依赖减弱.

对于大回线源，余弦变换的精度对高频限的依赖性大，只要高频上限大于10⁷ Hz，有合适的带宽，计算精度基本满足.

对于磁偶极子源，余弦变换的精度对低频限的依赖性更大，只要低频限大于10^-6 Hz，采用合适的带宽，计算精度满足误差要求.

通过最佳频率范围的对比，可以总结出，无论是那种因素的最佳频率范围大约都可以选择10^－6~10⁷ Hz.电阻率增大的时候可以适当的增大f_H来提高精度；回线半径和收发距增大时，可以适当的增大f_L或减小f_H，来提高余弦变换精度，但必须保持log^f_H－log^f_L≥12.利用上述的频率区间的选取规则，能够最大限度地提高余弦变换的精度，降低因为频段的选取对计算结果所产生的不良影响，从而为瞬变电磁的正演奠定基础.