2. 胜利油田分公司物探研究院, 东营 257000
2. Geophysical Research Institute of Shengli Oil-field Branch, Dongying 257022, China
0 引 言
在地震数据采集设计中,通常会将炮点和检波点位置放在规则的网格之下,但是由于野外地形条件限制,检波点的位置通常是不规则的,这就导致地震数据的不规则采样,出现地震道缺失.同时,在采集过程中,不可避免地会采集到环境及人为造成的随机噪声干扰,虽然叠加处理可以去除一部分随机噪声,但噪声残余以及道缺失现象在地震数据中仍然是普遍存在的,而大多数成像方法都不适用于不规则的地震数据,这将大大影响成像效果以及后期的解释成果(李振春和张军华,2004;陆基孟和王永刚,2009).因此,进行数据重建和去噪研究具有十分重要的意义.
用于数据重建的方法通常包括四类,一种方法是将地震数据变换到其他域,如傅里叶变换(Liu and Sacchi, 2004)、曲波变换(Herrmann et al,2008)等,这种方法是建立在数学变换以及信号分析的基础上的.另一种方法基于预测滤波器,它利用地震信号在频率域的可预测性( Abma and Claerbout, 1995).还有一类是基于波动方程的重建方法,如DMO和反DMO交替进行的规则化方法、方位角时差变换法(Chemingui and Biondi, 2002)等.第四种是基于奇异值分解的矩阵秩减方法(Oropeza,2010),利用地震数据的相干性进行插值数据重建.此外,奇异值分解也可以用于随机噪声的压制(Eckart and Yong, 1936;吴亚东等,2003;冯兴强等,2005;Sacchi,2009; Oropeza,2010; Oropeza and Sacchi, 2010;沈鸿雁和李庆春,2010;Xue et al., 2013;鲍伟和马继涛,2013).但是,现有的方法大都不能在数据重建时同时进行去噪处理.
相对于其他去噪和数据规则化方法,奇异谱分析(即频域奇异值分解方法)基于地震数据的相干性压制随机噪声,并可以通过迭代进行地震数据重建(Schoellhamer,2001;Oropeza,2010),但现有的迭代公式不能进行噪声压制.本文改进奇异谱分析进行数据重建的迭代公式,在迭代时自动在地震道缺失的位置进行插值,在不缺失地震道的位置压制噪声,插值结束后自动进行一次去噪.此外在插值时,将每次迭代时一次性插值改为按信号分量的能量分步插值.最后,本文将新的迭代公式应用到合成记录和实际资料的去噪和规则化处理中,并将改进公式的处理结果与分别规则化和去噪的结果相对比,分析这种方法在去噪和规则化处理中的优势和局限性.
1 方法原理
1.1 基于奇异谱分析的去噪原理
对于一个含有k个线性无关的同相轴的地震记录,当把它的任一频率分量插入到Hankel矩阵中后,Hankel矩阵的秩为k.但是,当地震记录中混入随机噪声或者地震记录缺失地震道时,Hankel矩阵的秩就会增加,如图 1所示.因此,地震记录的去噪和数据重建问题就可以归结为Hankel矩阵的秩减问题(Eckart and Yong, 1936).基于奇异谱分析去噪的流程(Oropeza and Sacchi, 2010)为:
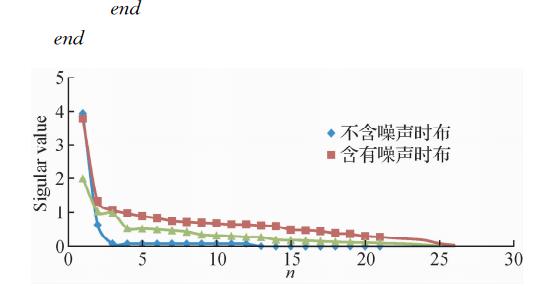 | 图 1 Hankel矩阵奇异值分布图 Fig. 1 Singular value distribution of Hankel matrix |
(1)通过傅里叶变换将地震信号变换到频率-空间域为
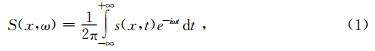
(2)将每一频率分量插入Hankel矩阵
假设 S ω=[ S1,S2,S3,…,S Nx]T表示地震信号的某一频率分量,Nx表示空间采样点数.然后,将这一频率分量插入到Hankel矩阵中:
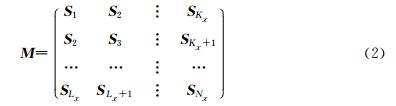
(3)对Hankel矩阵进行奇异值分解;

(4)Hankel矩阵的秩减;
对分解得到的 U、Σ、V 进行截断处理,截取前k列,得到矩阵 M的近似矩阵M k,k即为近似矩阵 M k的秩.如(4)式所示:

(6)通过傅里叶逆变换将数据变换回时域.
1.2 基于奇异谱分析的数据重建原理
地震道的缺失也会使Hankel矩阵的秩增加,同样地,通过矩阵秩减可以进行数据重建.为了得到更好的重建效果,可以通过迭代的方法对Hankel矩阵进行插值,从而减小重建后的信号与原信号的振幅差.基于奇异谱分析的数值重建原理可以由下式表示为
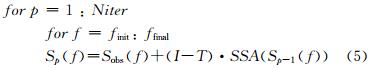
其中,finit和ffinal代表进行奇异谱分析的最小频率和最大频率,Sobs(f)表示缺失了地震道的观测数据,矩阵 I 是一个元素全部为1的矩阵,T为采样算子,用以识别缺失的地震道位置.
在含有数据的地震道位置,算子T(i,j)的值为1;在缺失地震道的位置,算子T(i,j)的值为0.公式(5)中表示点乘,SSA()表示奇异谱分析过程,且奇异谱分析过程与去噪过程相同,Sp(f)表示每次迭代的得到的结果.
1.3 联合去噪和数据重建原理
使用公式(5)进行迭代时,在缺失地震道的位置通过奇异谱分析进行插值,不缺失地震道的位置保留观测数据Sobs(f),这种方法在观测数据不含噪声时可以取得很好的插值效果.但是,当地震数据含有噪声时,噪声也会被保留下来,且迭代时噪声的存在将降低数据的相干性,进而影响插值效果.为了在数据重建时压制噪声,本文将迭代公式进行了如下修改:
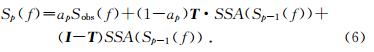
在不缺失地震道的位置,新迭代出的数据由apSobs(f)和(1-ap)T·SSA(Sp-1(f))两部分组成,前者为原始的观测数据,后者为奇异谱分析后的数据.ap控制每次迭代后两者所占比例,在迭代过程中,ap从1.0开始减小,保留的原始数据越来越少,其值逐渐被奇异谱分析后的值所替代,随机噪声得到压制.在ap=0时,公式(6)变为:

在缺失地震道的位置,公式(6)与公式(5)等价.
此外,在每次迭代时,本文做了一些优化:将一次性插值改为分步插值,先对信号能量强的部分(大奇异值所对应的部分)进行插值,再和信号能量较弱的部分(小奇异值所对应的部分)一起进行插值.对能量强的部分插值时效果较好,可以改善整体数据的相干性,有利于提高弱能量部分插值的正确性.
基于奇异谱分析的联合规则化、去噪处理的流程如图 2所示.虚线框中的部分为奇异谱分析的过程,nit为给定的最大迭代次数,a为每次a减小的步长,nw为频率分量的个数.
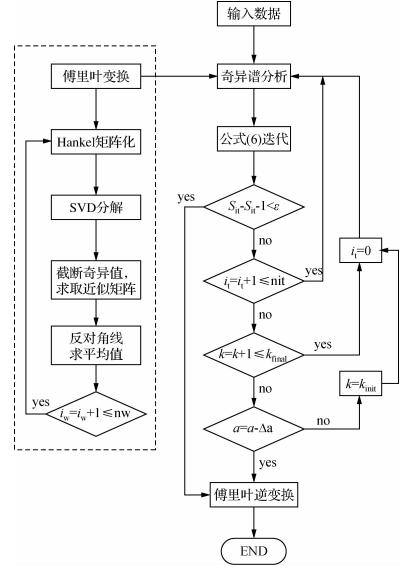 | 图 2 基于奇异谱分析的联合数据规则化及去噪处理流程图 FigFig. 2 Flow chart of simultaneous 2D seismic data de-noising and regularization method |
2.1 合成地震记录
为了验证联合方法的有效性,本文对一个只含有两个相互独立线性同相轴的合成剖面进行规则化处理.用一个采样算子T抽掉了大约50%的地震道,但不添加噪声.在这个二维地震剖面中,每道72个采样点,采样间隔为0.02 s.对图 3b中的地震记录进行规则化处理,图 3c、图 3d分别为使用原始迭代公式和改进迭代公式后的结果,图 3e、图 3f是两者与原剖面的差.通过对比图 3,得到如下认识:
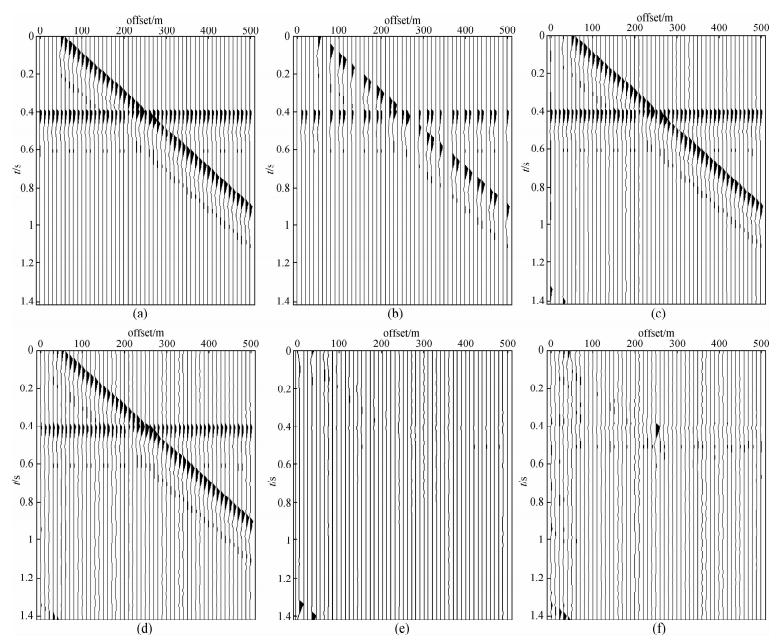 | 图 3 联合去噪及规则化算法与原算法处理效果对比图 (a)原始二维自激自收剖面;(b)抽取了约50%地震道的自激自收剖面; (c)原始迭代公式(5)的计算结果;(d)联合方法处理结果; (e)公式(5)的计算结果与初始记录的差;(f)联合方法处理结果与初始记录的差. Fig. 3 Regularization result of original algorithm and improved algorithm (a)Synthetic section;(b)Section with 50% traces off;(c)The calculated result of original algorithm;(d)The calculated result of improved algorithm;(e)Difference section of originalalgorithm;(f)Difference section of improvedalgorithm. |
(1)对于只缺失地震道不含噪声的地震记录,两种方法处理的结果相似,都可以得到很好地插值效果,同相轴连续性较好;
(2)对比差剖面,图 3f中可以看到微弱的有效信号.这是因为在含有地震数据的位置,经过奇异谱分析的信号与原信号存在微弱的振幅差.
为了进一步验证联合方法的优势,本文在图 3b中的地震记录上添加了有效信号最大振幅50%的随机噪声(按有效信号最大振幅计算),然后再分别使用两种迭代公式进行处理,最后再对由公式(5)重建后的数据进行一次去噪处理,比较三者的效果.在图 4中,图 4b、4c分别为使用原始和改进后的迭代公式进行处理得到的结果,图 4d是对图 4b中地震记录进行了一次SSA去噪后的结果,三者对比可以发现:
(1)改进后的迭代公式取得了较好的去噪和数据重建效果,而原始迭代公式处理的结果虽然同相轴连续性变好,但是随机噪声没有得到压制,改进后的公式去噪效果要优于原始迭代公式;
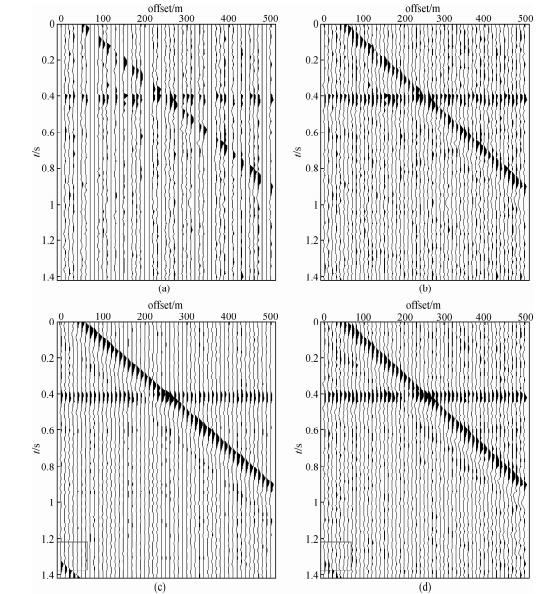 | 图 4 联合去噪及规则化算法与原算法处理效果对比图 (a)同时含有噪声和道缺失的剖面;(b)原始迭代公式(5)的计算结果; (c)联合去噪及规则化方法处理结果;(d)对(b)中记录进行SSA去噪结果. Fig. 4 Processing result of original algorithm and improved algorithm (a)Input data with noise and a loss of traces;(b)The regularization result of original algorithm; (c)The regularization result of improved algorithm;(d)SSA de-noising result of section(b). |
(2)将图 4c与4d对比,图 4c的信噪比要优于与图 4d,这是因为在迭代过程中,分步插值改善了数据相干性,取得了更好的去噪效果;
(3)在图 4c、4d的红框中出现了与倾斜同相轴平行的一个小的同相轴,这是在插值时插进来与倾斜同相轴相干的信号. 2.2 实际资料
图 5a为某探区一个101×501低信噪比叠后剖面,同时存在道缺失和随机噪声现象.为了验证联合方法对实际数据的处理效果,本文分别使用改进前后的迭代公式对这个叠加剖面进行处理,结果如图 5所示.图 5b和5c分别为改进的联合方法和原始迭代公式进行处理的结果,分析可以看出:
(1)图 5c中信号同相轴较为连续,并且具有良好的信噪比,这表明基于联合方法在进行实际资料处理时是有效的;
(2)在图 5b中可以看到明显的噪声,影响了有效信号的识别,尤其是在红色箭头所指区域,同相轴难以辨认.而在图 5c中,在与5b同一区域的同相轴可以识别.这验证了联合方法相对于原有方法的优越性.
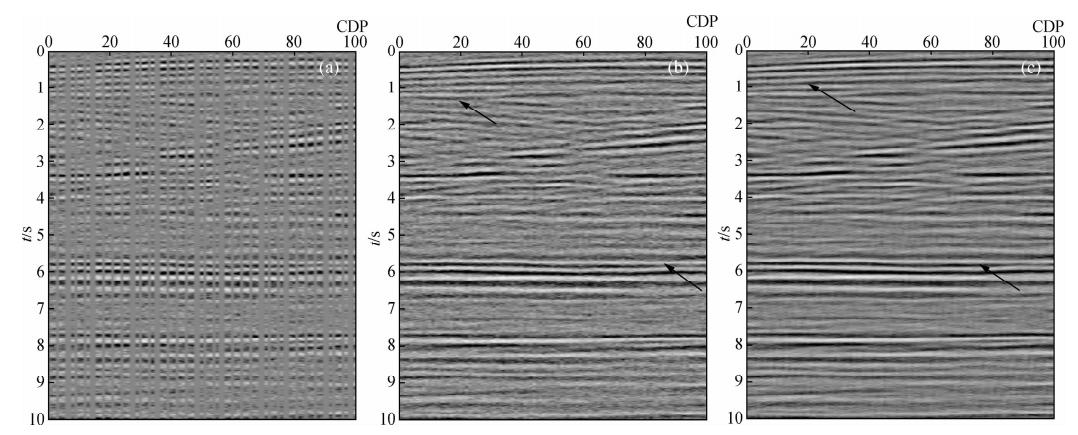 | 图 5 实际资料处理效果图 (a)某探区含缺失道低信噪比实际资料;(b)原始迭代公式计算的结果;(c)联合去噪及规则化方法处理结果. Fig. 5 Processing result of two methods to field data (a)Input field data with low SNR and a loss of traces; (b)The regularization result of original algorithm; (c)The regularization result of improved algorithm. |
本文实现了基于奇异谱分析的联合去噪及规则化处理方法,并通过对合成记录和实际资料的处理,得到了如下几点认识:
(1)改进的联合去噪、规则化方法能够在补全缺失地震道的同时进行随机噪声压制,提高计算效率;
(2)通过分步插值改善数据相干性,提高了去噪效果;
(3)对于倾角较大的倾斜同相轴,插值时会插入部分非有效的相干信号,这在改进前后的算法中都是无法避免的.
改进的算法仍然不能完全压制随机噪声,这是因为每次只将单一频率分量插入Hankel矩阵造成的.如果每次向Hankel矩阵中插入多个频率分量,就可以得到更好的去噪效果(Oropeza and Sacchi, 2009).这个问题在进行三维地震数据去噪时也能得到改善,因为在三维地震数据去噪时向Hankel矩阵中插入一个三维数据体,具有更多的信息.最后,需要强调的是本文提出的联合去噪、规则化算法可以很好地推广到三维地震数据规则化和去噪以及多频率SSA方法中.
致 谢 作者感谢国家自然科学基金(41104069,41274124),国家973课题(2014CB239006,2011CB202402),山东省自然科学基金(ZR2011DQ016),中央高校基本科研业务费专项基金(R1401005A)及骨干教师人才支持计划联合资助.
| [1] | Abma R, Claerbout J. 1995.Lateral prediction for noise attenuation by t-x and f-x techniques[J]. Geophysics, 60(6): 1887-1896. |
| [2] | Chemingui N, Biondi B. 2002. Seismic data reconstruction by inversion to common offset[J]. Geophysics, 67(5): 1575-158 |
| [3] | Eckart C, Young G. 1936. The approximation of one matrix by another of lower rank[J]. Psychometrika,1(3): 211-218. |
| [4] | Liu B, Sacchi M D. 2004. Minimum weighted norm interpolation of seismic records[J]. Geophysics, 69(6): 1560-1568. |
| [5] | Oropeza V E, Sacchi M D. 2009. Multifrequency singular spectrum analysis[C].Expanded Abstracts of 77th Annual Internat SEG Mtg,3193-3197. |
| [6] | Oropeza V E. 2010.The singular spectrum analysis method and its application to seismic data denoising and reconstruction[D].Canada: University of Alberta. |
| [7] | Oropeza V E, Sacchi M D. 2010. A randomized SVD for multichannel singular spectrum analysis (MSSA) noise attenuation[C]//80th Annual International Meeting, SEG, Expanded Abstracts.1989-1992. |
| [8] | Sacchi M D. 2009. FX singular spectrum analysis[C]//CSPG CSEG CWLS Convention,392-395. |
| [9] | Schoellhamer D H. 2001.Singular spectrum analysis for time series with missing data[J]. Geophysical Research Letters, 28(16): 3187-3190. |
| [10] | Xue Z G, Huang J, Li Z C, et al. 2013.De-noising Method for 3D Field Data Based on the MSSA[C]//75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013. |
| [11] | 鲍伟, 马继涛. 2013. 频率域奇异值分解压制随机噪声方法[J]. 科技导报, 31(21): 58-63. |
| [12] | 冯兴强, 杨长春, 龙志祎. 2005. 基于奇异值分解的 f-x-y 域滤波方法[J]. 物探与化探, 29(2): 171-173. |
| [13] | 李振春, 张军华. 2004. 地震数据处理方法[M]. 北京: 中国石油大学出版社. |
| [14] | 陆基孟, 王永刚. 2009.地震勘探原理[M]. 北京: 中国石油大学出版社. |
| [15] | 沈鸿雁, 李庆春. 2010. 频域奇异值分解 (SVD) 地震波场去噪[J]. 石油地球物理勘探, 45(2): 185-189. |
| [16] | 吴亚东, 符溪, 文鹏飞,等. 2003. 奇异值分解压制随机噪声的方法及应用[J]. 新疆石油地质, 24(2): 144-145. |
 2014, Vol. 29
2014, Vol. 29

