地球物理学进展  2014, Vol. 29 Issue (4): 1512-1517   PDF    
引用本文
穆大鹏, 郭金运, 孙中昶, 孔巧丽. 基于主成分分析的GRACE重力场模型等效水高[J]. 地球物理学进展, 2014, 29(4): 1512-1517, doi: 10.6038/pg20140405  
MU Da-peng, GUO Jin-yun, SUN Zhong-chang, KONG Qiao-li. Equivalent water height from GRACE gravity model based on principal component analysis. Progress in Geophysics, 2014, 29(4): 1512-1517, doi: 10.6038/pg20140405   
基于主成分分析的GRACE重力场模型等效水高
穆大鹏1, 郭金运1,2 , 孙中昶3, 孔巧丽1,2    
1. 山东科技大学测绘科学与工程学院, 青岛 266590;
2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室, 青岛 266590;
3. 中科院遥感与数字地球研究所, 北京 100096
收稿日期: 2013-8-8 修回日期: 2013-12-13 .
基金项目：国家自然科学基金（40974004、41274018、41374009）和国际科技合作计划（2009DFB00130）联合资助.
作者简介：穆大鹏，男，1989年生，在读硕士，主要从事GRACE时变重力场研究.（E-mail：mdp321@126.com）
通讯作者：郭金运，男，1969年生，博士，教授，博士生导师，主要从事空间大地测量、物理大地测量和海洋大地测量等研究.（E-mail：jinyunguo1@126.com）
摘要：本文使用主成分分析在空间域提取GRACE重力场模型的等效水高，假设信号与噪声之间统计不相关，把由CSR、GFZ和JPL的GRACE重力场模型计算得到的等效水高值作为统计量，通过线性变换来分离信号和噪声.选择2007年3月份GRACE重力场模型作为实验，在直接分离没有取得预期结果后，对GRACE作半径为300 km、400 km和500 km的高斯平滑，然后利用主成分分析得到了3个模式.结果显示，3种平滑半径下，主成分的第1模式的贡献率分别为79%、90%和93%.从主成分3个模式的统计结果以及等效水高图判断，第1模式对应于水文变化信号，其他2个模式为南北条带状噪声.由主成分的第1模式估算了CSR、GFZ和JPL的等效水高，与经验去相关方法进行了对比，结果较为一致.2010年12个月的结果显示，第1模式的贡献率不仅与平滑半径有关，而且与时间有关.
关键词： 主成分分析     GRACE重力场模型     等效水高    
Equivalent water height from GRACE gravity model based on principal component analysis
MU Da-peng1, GUO Jin-yun1,2 , SUN Zhong-chang3, KONG Qiao-li1,2    
1. College of Geometrics, Shandong University of Science and Technology, Qingdao 266590, China;
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef of NASMG, Qingdao 266590, China;
3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China
Abstract: Gravity Recovery and Climate Experiment (GRACE) satellite can provide time-variable gravity field every month with spatial resolution 300-400 km. Monthly solutions from GRACE suffered so called north-south stripes noise which needed to be removed by filter approach. Many methods have been proposed and focus on filtering the spherical harmonic coefficients. In this paper, we use principal component analysis (PCA) to extract equivalent water height (EWH) from GRACE in spatial domain, which based on the assumption that signal and noise are uncorrelated. One of the main characteristics of PCA is taking advantage of different GRACE models produced by different groups, i.e., Center for Space Research (CSR), Jet Propulsion Laboratory (JPL), GeoForschungs Zentrum (GFZ). We view the GRACE gravity model released by CSR, GFZ and JPL as statistical variables, and separate the signal and noise by linear transformation, e.g., the orthogonal matrix derived by PCA. First of all, we choose the GRACE model of March, 2007 as an example to apply PCA. Unfortunately, we didn't obtain the anticipative result when we decomposed the EWH directly. We did obtain 3 components which are very similar to each other, but none of them can match the signal or noise. The possible reason is that our assumption is too simple for the relation between signal and noise from GRACE, so we choose Gaussian smoothing with 300 km, 400 km and 500 km to pre-process GRACE solutions, and then decompose the EWH. In this time, 3 different components are obtained using principal component analysis. The result showed that the first mode of three radiuses contributes to 79%, 90% and 93% of total variation, respectively. According to the statistical results and EWH maps, the first mode can be viewed as signal and others noise. We use the first mode to estimate the EHW of CSR, GFZ and JPL, and they are close to the result of Empirical De-correlation Method. Also, the result of 2010 showed that the contribution of first mode not only depended on smoothing radius, but also depended on time.
Key words: principal component analysis     GRACE gravity model     equivalent water height    

0 引 言

GRACE重力卫星计划由美国宇航署(NASA)和德国空间飞行中心(DLR)联合开发，于2002年3月成功发射，可以探测地球重力场的时变特征，其空间分辨率为300 km至400 km，时间分辨率为10天至30天(Tapley et al., 2004).GRACE时变重力数据自公开以来，被广泛应用于地球表面质量变化的研究，比如监测大尺度流域的陆地水储量变化以及干旱情况(苏晓莉等2011;冯伟等，2012；李琼等，2013)，研究南极和格陵兰岛的冰川质量变化(Luthcke et al., 2006；罗志才等，2012；丁明虎，2013)，冰川消融对海平面变化的影响(鄂栋臣等，2009)，以及监测地面重力的长期变化(邢乐林等，2012).

GRACE重力场模型位系数受卫星轨道误差、模型误差等因素影响，其高阶部分含有较多噪声(Huang et al., 2012)，对反演结果影响较大，其等效水高图被南北条带状噪声占据，很难观察到需要的信号.为提高估算精度，通常是对GRACE位系数进行某种限制措施，比如常见的高斯平滑核函数，降低高阶位系数的权重，来减少其含有的噪声(Wahr et al., 1998)；通过拟合多项式的方法剔除位系数的相关误差(Swenson and Wahr， 2006; Duan et al., 2009)；基于先验信息构造非各向同性平滑核函数(Kusche，2007)；利用统计方法对时间序列的GRACE位系数进行分析(Wouters and Schrama， 2007；Davis et al., 2008)，构造平滑核.

以上方法均是对一个研究机构发布的GRACE重力场模型进行处理，并且是使用平滑核函数对位系数进行限制.Frappart把CSR(Center for Space Research)、GFZ(GeoForschungs Zentrum)和JPL(Jet Propulsion Laboratory)的GRACE重力场模型作为三个观测值(Frappart et al., 2010；2012)，对信号和噪声做出统计独立的假设，利用独立成分分析(Independent Component Analysis，ICA)，从空间域获取地球表面的质量变化.本文将CSR、GFZ和JPL的GRACE重力场模型作为统计量，假设信号和噪声统计不相关，使用主成分分析(Principal Component Analysis，PCA)从空间域提取等效水高.我们首先选择2007年3月份GRACE重力场模型作为实验，使用主成分分析分离信号和噪声；然后又解算得到2010全年12个月的结果，证明主成分分析可以适用于时间序列的GRACE重力场模型.

1 主成分分析

主成分分析将原统计变量通过线性变换得到新变量，新变量之间统计不相关(Jolliffe，2002).假设 x1，x2，…，x n为统计变量，经过线性变换，得到新变量 p1，p2，…，p n，即：

式中，X=(x1 x2 … xn)，P=(p1 p2 … p n)，E是线性变换矩阵，它由统计变量X 的协方差矩阵计算得到.假设该协方差矩阵为C，那么它是一个n×n阶对称矩阵.通过求解矩阵C的特征值和特征向量，可以将其分解成为

式中，D 是对角阵，对角线上的元素λ1≥λ2…≥λn是矩阵 C的特征值，同时等于对应主成分的方差，E是由特征向量构成的正交矩阵，满足EE T=I，I是单位矩阵.因此，在公式(1)两边右乘以矩阵 E T，得到

如果选取前 k个特征值较大的新变量P k=(p1 p2 … p k)，可以由选择的新变量重构原统计变量，得到 X PCA，以达到压缩噪声的目的：

式中，E k表示由选择的特征向量构成的矩阵.重构变量 X PCA所包含的信息可以由贡献率α来衡量，即：

式中，λj表示特征值，n表示特征值总的个数，k表示选取的个数.

2 GRACE重力场模型

GRACE重力场模型的数据主要由CSR、GFZ、JPL等科研机构处理并对外公布，本文使用的数据是最新版本的Level-2 GRACE RL05数据.这些机构解算在GRACE重力场模型时，使用了相同的原始数据以及时间、坐标系统(Bettadpur，2012；Watkins，2012；Dahle et al., 2012)，它们所反映的地球重力场信息必然含有类似的成分，包括信号和噪声.但由于使用的地球物理模型、计算软件和方法的不同，其包含的信号尺度和噪声水平也必然有所区别.表 1给出了CSR、GFZ和JPL在解算重力场时使用的地球物理模型和方法的对比.从表中可以看出，CSR与JPL在使用的地球物理模型区别不大，主要区别是使用的软件不同；而GFZ与CSR、JPL的差异较大，不但使用的软件不同，而且模型也有很大差异.

表 1 GRACE重力场模型比较 Table 1 The comparison of different GRACE gravity models

由于这些GRACE重力场模型的异同点，使得它们包含的信号尺度和噪声水平不同.于是我们做出假设，认为信号与噪声统计不相关，尝试利用主成分分析，把CSR、GFZ和JPL的GRACE重力场模型作为三个统计量，来分离信号和噪声.

地球表面的质量异常可以由GRACE重力场模型的位系数残差计算得到，由于GRACE含有较多噪声，通常构造平滑核函数对位系数进行限制(如果不平滑则核函数的数值为1)来提高估算精度，经过平滑之后的质量异常可以由下式计算(Wahr et al., 1998)：

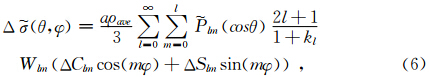
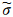式中，θ和φ分别为地心余纬和地心经度，Δ 表示质量异常，a为地球平均半径，ρave为地球平均密度(=5517 kg/m3)，P lm是规格化缔合勒让德函数，kl表示负荷勒夫数，Wlm表示平滑核函数，ΔClm和ΔSlm为GRACE位系数残差.质量异常Δ 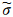除以水密度ρw(=1000 kg/m3)就得到等效水高，即：

3 等效水高的主成分分析

本文把CSR、GFZ和JPL的等效水高值作为三个统计量，尝试利用主成分分析，在空间域分离信号和噪声.GRACE位系数残差由以下方式计算得到：将2003年至2012年共120个月Level-2 GRACE RL05位系数求平均(对于缺少数据的月份，利用其前后两个月的平均值代替)，再将平均值从每个月的位系数中扣除得到残差.首先，我们选择了2007年3月份的GRACE重力场模型等效水高值作为实验，原因是水文变化在亚马逊流域、刚果河流域等地区较为活跃，同时便于从等效水高图中观察分离的结果.

由公式(6)、(7)分别计算得到CSR、GFZ和JPL全球1°经纬格网点的等效水高值，再将每个机构的数值按照经纬度顺序排列成具有360×180=64800个元素的列向量(相当于把360×180的矩阵拉直成为一个列向量)，这样三个机构的观测值就组成了64800×3的矩阵 X=(EWH CSR EWH GFZ EWH JPL)，作为统计量.需要特别指出的是，在公式(5)中，我们没有采取平滑，也就是Wlm的值均为1.未经平滑得到的等效水高值含有较多噪声，正是如此，我们才假设信号与噪声统计不相关，使用主成分分析从空间域分离信号和噪声.

在得到统计量 X之后，通过公式(2)计算其特征向量构成的线性变换矩阵E，再由公式(1)，得到主成分的三个模式.结果显示，所得到三个模式的等效水高图均为南北条带状，并且它们的方差接近，也就是说主成分分析没有实现信号与噪声的分离.我们认为GRACE含有信号和噪声并不能满足统计不相关的假设，需要采取其他手段对噪声进行抑制，然后再使用主成分分析进一步分离噪声.比如高斯平滑(汪汉胜等，2007；周旭华等，2006)，在一定半径平滑之后，仍然残余较多的南北条带状噪声，并且这种噪声水平和空间分布在不同机构的GRACE重力场模型中不同(Werth et al., 2009).

本文选择使用平滑半径为300 km、400 km和500 km的高斯平滑核函数，对GRACE重力场模型作预处理，然后再使用主成分分析进一步分离残余的噪声.即，在使用公式(6)、(7)计算等效水高值的时候，使用了高斯平滑核函数Wlm，然后再组成统计量X，进行主成分分析.

研究发现，在平滑半径为300 km、400 km和500 km时，主成分分析实现了残余噪声与信号的分离，其第一模式的贡献率分别为79%、90%和93%，在亚马逊流域等地区可以观察到较强的水文信号，而其他两个模式均为南北条带状噪声.表 2给出了不同平滑半径下主成分3个模式的统计结果，图 1左边为主成分3个模式的等效水高图.

表 2 不同平滑半径下主成分3个模式统计结果 Table 2 The statistical result of 3 principal component

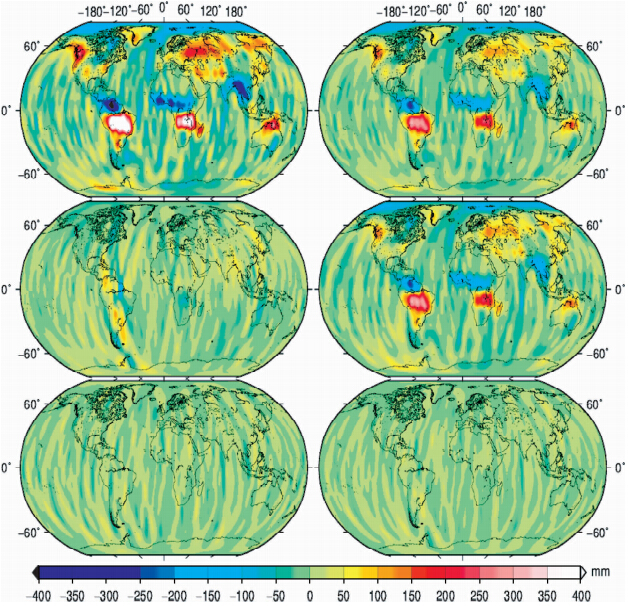图 1 平滑半径为400 km时等效水高图：左边由上至下为PC1-PC3；右边为CSR的结果，由上至下分别PCA，EDM以及二者之差 Fig. 1 EWH maps with 400 km radius: left，from top to bottom: PC1-PC3; right are the results of CSR，from top to bottom: PCA，EDM and the difference

至此可以看出，主成分分析不能直接实现信号与噪声的分离，需要高斯平滑来移除一部分噪声，然后再分离出残余的南北条带噪声，这种统计方法与GRACE的去相关滤波(Empirical De-correlation Method，EDM)十分相近.去相关滤波是通过拟合多项式来移除位系数的相关误差，就是移除等效水高图中的南北条带噪声.去相关滤波是在频谱域内完成，而主成分分析是在空间域内实现.下面我们比较了两种方法的结果.

从前面分析得知，主成分的第一模式PC1为分离得到的信号，因此，我们选择该模式来重构统计量 X，分别得到PCA估算CSR、GFZ和JPL等效水高值的结果.由公式(4)，选择第1模式进行重构：

如果详细展开，得则到：

式中，EWH PCACSR，EWH PCAGFZ，EWH PCAJPL分别为PCA估算CSR、GFZ和JPL的等效水高，e11，e21，e31是矩阵E 第1列向量中的元素，PC 1是主成分的第1模式.表 3给出了不同平滑半径下PCA与EDM的对比.图 1右边为PCA和EDM的等效水高图.

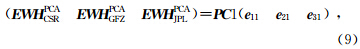
表 3 不同平滑半径下PCA与EDM对比 Table 3 The comparison of PCA and EDM with different radius

从表 3可以看出，在平滑半径为300 km时，EDM估算GFZ的最大值要高于PCA 85 mm，而CSR和JPL分别为38 mm、25 mm；在均方根方面，不同平滑半径下，无论是由PCA还是EDM得到的结果，CSR与JPL较为接近，而GFZ与前两者差异较大，其原因可能是，在计算GRACE重力场模型中，CSR和JPL使用的地球物理模型较为一致，主要区别在于使用的软件，而GFZ与它们在模型使用和计算软件方面都有较大区别，从而导致等效水高的结果也有着较大区别.

以上分析只是2007年3月的结果，为证明主成分分析可以适用于时间序列的GRACE重力场模型，本文计算了2010全年12个月的结果.结果显示，主成分第一模式的贡献率不仅与选择的平滑半径有关，而且与时间有很大关系，如图 2，400 km平滑半径时，6月份只有84%，在而2、3、4、8、9、10、11这些月份均超过了90%，其中9月份达到了94%.

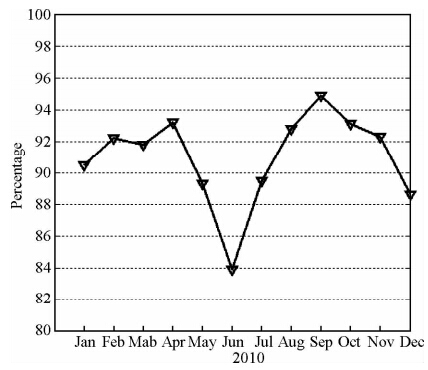图 2 400 km平滑半径时第1模式的贡献率 Fig. 2 The percentage of first mode with 400 km radius

同时，从图 3可以看到，在不同月份，尽管使用主成分分析分离了信号与噪声，但仍有残余的南北条带噪声.在上半年，这种残余噪声水平较少，而在下半年较多，尤其是在9月份与10月份.

图 3 2010年400 km平滑半径时CSR等效水高图 Fig. 3 EWH maps of CSR with 400 km radius in 2010
4 结 论

4.1    本文利用主成分分析，把CSR、GFZ和JPL的等效水高值作为三个统计量，并且假定GRACE重力场模型的信号与噪声之间统计不相关，从空间域对两者进行分离.由于GRACE重力场模型的位系数含有较大噪声，直接进行分离时，没能取得理想的结果，所以首先使用高斯平滑来移除一部分噪声，然后在进行分离.对于2007年3月份的GRACE重力场模型，当平滑半径为300 km、400 km和500 km时，第一模式的贡献率分别为79%、90%和93%，包含了重力场的绝大部分信息.从主成分3个模式的统计结果以及等效水高图判断，第1模式可以认为是信号部分，而其他2个模式可以视为噪声.通过主成分的第1模式进一步估算了CSR、GFZ和JPL的等效水高值，与经验去相关(EDM)进行了对比.在相同平滑半径下，两者结果较为一致.2010年12个月的结果表明，主成分第1模式的贡献率不仅与平滑半径选择有关，而且与时间有关.

4.2    使用主成分分析直接分离信号与噪声，没有成功，原因可能在于我们所作出的假设较为简单，GRACE重力场含有的信号与噪声远比统计不相关复杂；主成分分析的实现，需要采用必要的预处理来减弱一部分噪声，然后再从空间域分离信号与噪声.从主成分分析的过程来看，与经典的去相关滤波十分类似，只是后者在频谱域内实现，主成分分析是在空间域内实现，但两者的结果较为一致.今后，可以尝试深入分析信号与噪声的关系，探索从空间域分离信号与噪声的其他方法.

致 谢 感谢德国ISDC提供的GRACE Level-2 RL05时变重力场数据.

参考文献
[1] Bettadpur S. 2012. UTCSR Level-2 processing standards document for level-2 product release 0005[R]. Center for Space Research, The University of Texas at Austin. GRACE 327-742, Rev 4.0.
[2] Dahle C, Frank F, Christian G, et al. 2012. GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005[R]. Potsdam.
[3] Davis J, Tamisiea M E, Elosegui P, et al. 2008. A statistical filtering approach for Gravity Recovery and Climate Experiment (GRACE) gravity data[J]. J. Geophys. Res., 113(B4), B04410.
[4] Ding M H. 2013. An up to data review on the mass balance over Antarctica[J]. Progress in Geophys. (in Chinese), 28(1): 24-35.
[5] Duan X J, Guo J Y, Shum C K, et al. 2009. On the post-processing removal of correlated errors in GRACE temporal gravity field solutions[J]. J. Geod., 83(11): 1095-1106.
[6] E D C, Yang Y D, Chao D B. 2009. The sea level change from the Antarctic ice sheet based on GRACE[J]. Chinese J. Geophys. (in Chinese), 52(9): 2222-2228.
[7] Feng W, Lemoine J M, Zhong M, et al. 2012. Terrestrial water storage changes in the Amazon basin measured by GRACE during 2002-2010[J]. Chinese J. Geophys. (in Chinese), 55(3): 814-812.
[8] Frappart F, Ramillien G, Maisongrande P, et al. 2010. De-noising satellite gravity signals by independent component analysis[J]. Geosci. Remote Sens. Lett., 7(3): 421-425.
[9] Frappart F, Ramillien G, Leblanc M, et al. 2012. An independent component analysis filtering approach for estimating continental hydrology in the GRACE gravity data[J]. Remote Sens. Environ., 115(1): 187-204.
[10] Huang J L, Halpenny J, van der Wal W, et al. 2012. Detectability of groundwater storage change within the Great Lakes Water Basin using GRACE[J]. J. Geophys. Res., 117(B8), B08401.
[11] Jolliffe I T. 2002. Principal component analysis[M]. New York: Springer.
[12] Kusche J. 2007. Approximate de-correlation and non-isotropic smoothing of time-variable GRACE-type gravity field models[J]. Journal of Geodesy, 81(11): 733-749.
[13] Li Q, Luo Z C, Zhong B, et al. 2013. Terrestrial water storage changes of the 2010 southwest China drought detected by GRACE temporal gravity field[J]. Chinese J. Geophys. (in Chinese), 56(6): 1843-1849.
[14] Luo Z C, Li Q, Zhang K, et al. 2012. Trend of mass change in the Antarctic ice sheet recovered from the GRACE temporal gravity field[J]. Sci. China Earth Sci., 55(1): 76-82.
[15] Luthcke S B, Zwally H J, Abdalati W, et al. 2006. Recent Greenland ice mass loss by drainage system from gravity observations[J]. Science, 314(5803): 1286-1289.
[16] Su X L, Ping J S, Ye Q X. 2011. Terrestrial water variations in the North China Plain revealed by the GRACE mission[J]. Sci. China Earth Sci., 54(12): 1965-1970.
[17] Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data[J]. Geophys. Res. Lett., 33, L08402.
[18] Tapley B D, Bettadpur S, Ries J C, et al. 2004. GRACE measurements of mass variability in the Earth system[J]. Science, 305(5683): 503-505.
[19] Wahr J,Molenaar M,Bryan F.1998. Time variability of the Earth's gravity filed: Hydrological and oceanic effects and their possible detection using GRACE[J]. J Geophys. Res., 103(B12): 30205-30229.
[20] Wang H S, Wang Z Y, Yuan X D. 2007. Water storage changes in Three Gorges water systems area inferred from GRACE time-variable gravity data[J]. Chinese J. Geophys.(in Chinese), 50(3): 730-736.
[21] Watkins M. 2012. JPL Level-2 processing standards document for Level-2 product release 05 GRACE 327-741[R]. Jet Propulsion Laboratory. Rev. 4. 0.
[22] Werth S, Gunter A, Schmidt R, et al. 2009. Evaluation of GRACE filter tools from a hydrological perspective[J]. Geophysical Journal International, 179(3): 1499-1515.
[23] Wouters B, Schrama E O. 2007. Improved accuracy of GRACE gravity solutions through empirical orthogonal function filter of spherical harmonics[J]. Geophys. Res. Lett., 34(23), L23711.
[24] Xing L L, Li H, Xuan S B, et al. 2012. Long-term gravity changes in Chinese mainland from GRACE and terrestrial gravity measurements. Chinese J. Geophys. (in Chinese), 55(5): 1557-1564.
[25] Zhou X H, Wu B, Peng B B. 2006. Detection of global water storage variation using GRACE[J]. Chinese J. Geophys. (in Chinese), 49(6): 1644-1650.
[26] 丁明虎. 2013. 南极冰盖物质平衡最新研究进展[J]. 地球物理学进展, 28(1): 24-35.
[27] 鄂栋臣, 杨元德, 晁定波. 2009. 基于GRACE资料研究南极冰盖消减对海平面的影响[J]. 地球物理学报, 52(9): 2222-2228.
[28] 冯伟, Lemoine J M, 钟敏,等. 2012. 利用重力卫星GRACE监测亚马逊流域2002-2010年的陆地水变化[J]. 地球物理学报, 55(3): 814-821.
[29] 李琼, 罗志才, 钟波,等. 2013. 利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J]. 地球物理学报, 56(6): 1843-1849.
[30] 罗志才, 李琼, 张坤,等. 2012. 利用GRACE时变重力场反演南极冰盖的质量变化趋势[J]. 中国科学: 地球科学, 2012, 42(10): 1590-1596.
[31] 苏晓莉, 平劲松, 叶其欣. 2011. GRACE卫星重力观测揭示华北地区陆地水量变化[J]. 中国科学: 地球科学, 42(6): 917-922.
[32] 汪汉胜, 王志勇, 袁旭东. 2007. 基于GRACE时变重力场的三峡水库补给水系水储量变化[J]. 地球物理学报, 2007, 50(3): 730-736.
[33] 邢乐林, 李辉, 玄松柏,等. 2012. GRACE和地面重力测量监测到的中国大陆长期重力变化[J]. 地球物理学报, 55(5): 1557-1564.
[34] 周旭华, 吴斌, 彭碧波. 2006. 全球水储量变化的GRACE卫星检测[J]. 地球物理学报, 49(6): 1644-1650.