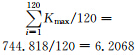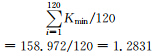2. 南京师范大学地理科学学院, 南京 210023;
3. 中科院南京地理与湖泊研究所湖泊与环境国家重点实验, 南京 210082
2. College of Geography, Nanjing Normal University, Nanjing 210023, China;
3. State Key Laboratory of Lake Science and Environment, Nanjing Institute of Geography and Limnology, Chinese Academy of Sciences, Nanjing 210082, China
0 引 言
太阳大气中发生的一系列物理现象统称为太阳活动.太阳活动周期一般是指11年、22年或更长时间的太阳黑子数目的多寡和太阳黑子群磁极性变换的周期变化(张桂清,2003).平均11.1年的太阳活动周期又称Schwabe-Wolf周期.也有学者对太阳黑子数和太阳黑子面积数周期进行分析得到太阳活动最显著的周期是10.69年(占腊生等,2006)和10.6年、10.9年(李可军等,2004).以往认为这些周期都是统计意义上的平均周期,并非严格的物理周期.太阳黑子是太阳活动中与太阳磁场极性有关的一种表现.太阳活动的其他一些现象,如太阳耀斑和太阳紫外线通量可能也显示出同样的周期旋回特征(Lean,1987).G.E.Hale于1908年的测量首次揭示了黑子中磁场更强.已知太阳磁场每隔11年倒转一次!这表明黑子周期在太阳磁场极性方面实际上是22年,这就是所谓的22年磁周期,又称海尔周期.多数学者是从太阳黑子数和太阳黑子相对数分析太阳活动规律(陈彪和印春霖,1965; Chernosky,1966; Lean,1997; Foukal,1998; Solanki and Fligge, 1998; 廖德春和廖新浩,2001; Kane,2002; 李可军等, 2004,2010; Le and Wang, 2004; 郭汉伟和乐贵明,2004; 乐贵明和王家龙,2004;占腊生等,2006; Ternullo,2007; Haigh.2007; 尹志强等,2007; de Jager,2008; Zolotova,2009; Charvátová,2009; Krivova, et al., 2010; Schrijver,2011; Scafetta,2012).也有少数学者从太阳磁场极性的22年磁周期分析太阳活动规律(Jose,1965;杨志根和赵铭,1988;杨志根,1991;曲维政等, 2004,2008;刘复刚和王健, 2013a,2013b).
太阳活动的周期性,应该首先是物理特征的重现性.太阳黑子11年活动周期只体现了黑子活动奇数周和偶数周黑子数或黑子相对数多少的集聚规律,恰恰丢失了太阳黑子磁极性每隔11年倒转一次的重要物理特征.根据曲维政等(2008)文中数据,我们绘出了太阳黑子磁极性指数图像(图 1a).如果将黑子磁极性指数为负值部分取绝对值就得到了图 1b,这就是通常所见到的太阳黑子数和太阳黑子相对数所反映出的太阳黑子活动的11周期.图 1a M1-M2,M2-M3,M4-M5,M6-M7时段图像陡缓变化和黑子正负磁极性转换处所体现的太阳黑子数变化特征的连续性,在图 1b相应时段就很难识别.
 | 图 1 太阳黑子磁极性指数特征与太阳黑子数变化特征的比较(曲维政等,2008数据) Fig. 1 Comparison between magnetic index and numbers of the Sunspot(data from reference Quwei-zheng,2008) |
Jose(1965)研究发现,太阳绕太阳系质心绕转的角动量变率具有178.76年周期,太阳绕瞬时曲率中心的角动量变率具有178.70年周期,并发现二者和太阳22年磁周期存在很好对应关系.刘复刚和王建(2013b)得出太阳轨道运动极值状态和轨道运动角动量变化等于零的相位是完全一致的.杨志根和赵铭(1988)在对太阳极性黑子相对数周期分析时指出:“太阳黑子活动在相当程度上是受到了行星运动所导致的日心轨道运动的牵制……,说明太阳黑子活动的周期性重复不是本身固有的,而是随(太阳轨道运动)角动量变率的周期性变化而变化,其变化周期约为178年”.太阳活动的22年磁周期与太阳轨道运动周期图像和太阳轨道运动角动量变率图像都有较好的对应关系(陈彪和印春霖,1965; Jose,1965; 杨志根和赵铭,1988;杨志根,1991;刘复刚和王建等, 2013a,2013b).这种探究似乎更接近问题本质,但还存在一个没能逾越的障碍,就是还没找到太阳轨道角动量和太阳自转角动量之间的本质联系.因为所有的太阳活动都是产生于或依附于太阳本体,所以要把研究太阳自转角动量变化作为攻克的目标.
1 太阳自转角动量和太阳轨道角动量之和守恒
“太阳系可作为一个孤立的力学子系统建立内部天体的动力学关系”(赵铭,2012).Jose(1965)根据整个太阳系的角动量守恒,探讨了太阳绕转角动量的变化.就整个太阳系而言,其“绝对方向”是不可观测的,而“由假定空间的‘绝对方向’的不可观测性,我们可以导出转动不变性,并得到角动量守恒(李政道等,2000).整个太阳系的角动量视为守恒可得(1)式为
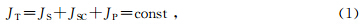
行星在围绕太阳系质心旋转时,太阳系的结构是变化的.例如,会出现8大行星位于太阳一侧和木星与其它行星分别位于太阳两侧的情形.这说明整个太阳系的质量分布相对太阳系质心发生了变化.由于JT=const,因此会导致整个太阳系的绕转速度发生变化.而整个太阳系的绕转速度是由太阳质心(S)和行星系统质心(P)同步绕太阳系质心(C)运动所决定(戴文赛,1979).因为行星首先遵从绕太阳系质心绕转,如若将太阳系质心视为太阳质心,则每个行星的绕转半径 L i始终通过力心,又因为L i与 F i的方向平行,所以每个行星的绕转角动量变化为:
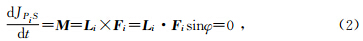

根据刘复刚和王建(2013b)创建的行星会合指数(K)运动学方程(见K表达式)得到的图像2可知,太阳系质心(C)和太阳质心(S)多半是不重合的.这说明每个行星绕太阳系质心绕转的角动量瞬时不守恒.然而,整个行星系统的轨道角动量则是守恒的.因为太阳系质心(C)始终位于行星系质心(P)和太阳质心(S)的连线上,这说明行星系质心(P)始终在引力 中心太阳(S)的引力作用线上,即P的绕转半径方向始终和太阳引力方向平行,所以整个行星系统绕转角动量瞬时守恒,K表达式为
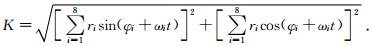
行星系统角动量守恒(JP=const)通过下面的统计分析也可以得到证明.根据行星会合指数运动学方程得到的2300~2400年周期中(如图 5)(刘复刚和王建等,2013a),任意选择平均13.5个(13~14个)连续的178~179年周期构成的一个完整的2403年哈尔斯塔(Hallstatt)长周期.根据图像得到2403年周期中每个峰值和谷值的K值(见表 1),然后求得峰值K1和谷值K2的平均值分别为K1=6.2068和K2=1.2831.理论上,所有行星都在太阳一侧会合,因行星总质量为446.66个地球质量(5.976×1024 kg)单位,这时行星系统角动量最大值为:
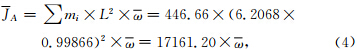
|
|
表 1 通过K指数图像获得的2403年周期中每个峰值和谷值的K值 Table 1 K-values of every peak and valley of 2403 years cycle inferred from K-index figure |
当行星系统处于最大分离状态时,除木星外,其它7颗行星按质量权重获得的权重半径之和为13.2144(AU)(实际上7颗行星不可能排成直列,故权重半径之和一定小于此值).如若这7颗行星与木星分居在太阳两侧且位于同一直线上,根据刘复刚和王建(2013b)文中表 2中质量权重半径ri得到,行星系统8颗行星除木星外的其它7颗行星的质量权重半径之和为3.826(AU).而通过表 1实际获得的平均极小值半径为1.2831(AU),即实际7颗行星的质量权重平均半径为木星的权重半径减去1.2831,即3.6983-1.2831=2.4152.就是说,行星系统中此7颗行星会合(与木星相背离,即日心黄经相差180°)质心距太阳质心(S)的实际长度是理论长度的0.6312(2.4152/3.826)倍.就7颗行星按质量权重获得平均半径为13.2144(AU)而言,实际平均半径只有8.341(AU)(0.6312×13.2144).这时整个行星系统的角动量最小值为木星和另外7颗行星的角动量之和,即
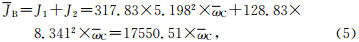
|
|
表 2 根据太阳自转角度变化峰值预测2000-2550年间太阳活动奇数周12个峰值出现的时间 Table 2 Occurring time prediction of the 12 odd cycles of the solar activity cycle during 2000-2550 according to the changes of the angular momentum of the Sun’s rotation |
因为J B/J A=1.0227,所以得到J A≈J B.这说明,行星系统高度会合与高度相背离时的两种极端状态下角动量相等.因为角动量的极大值和极小值相等,根据极限的夹逼定理推断整个行星系统的瞬时绕转角动量也应该守恒,这一结果验证了JP=const推论的正确性.因太阳自转角动量与太阳绕转角动量之和守恒,从而得到

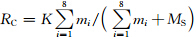 , 进而得到ω与K2呈线性负相关关系(刘复刚和王建等,2013c),见图 3.通过图 3上下两图的对比发现,太阳自转速度图像与行星会合指数图像的形态特征具有量值反向的完全一致性(如竖实线指示).这说明行星会合指数具有指代太阳自转速度的作用.因为行星会合指数改正后平均具有22年的周期规律,因此太阳自转速度也同样具有平均22年的周期性变化.太阳黑子活动与太阳自转速度变化特征的一致性更符合理论要求,为此,根据(6)式推导出太阳自转角速度变化与K指数的关系.
, 进而得到ω与K2呈线性负相关关系(刘复刚和王建等,2013c),见图 3.通过图 3上下两图的对比发现,太阳自转速度图像与行星会合指数图像的形态特征具有量值反向的完全一致性(如竖实线指示).这说明行星会合指数具有指代太阳自转速度的作用.因为行星会合指数改正后平均具有22年的周期规律,因此太阳自转速度也同样具有平均22年的周期性变化.太阳黑子活动与太阳自转速度变化特征的一致性更符合理论要求,为此,根据(6)式推导出太阳自转角速度变化与K指数的关系.
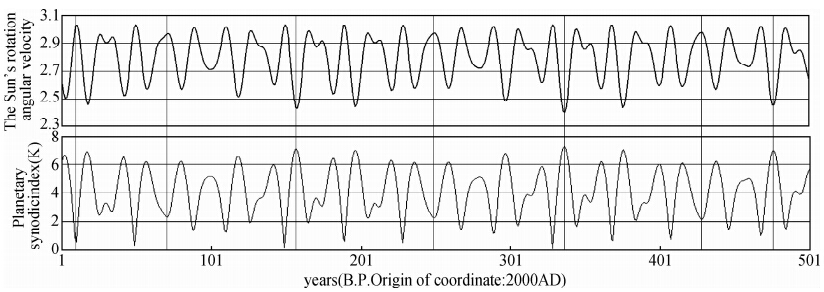 | 图 3 太阳自转速度(上图)与行星会合指数(下图)的比对) Fig. 3 Comparison of the solar rotation speed(above) and planetary synodic index(below) |
对(6)式两侧同时求导可得:
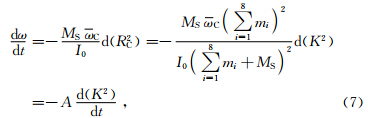
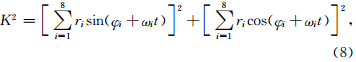
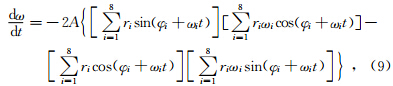
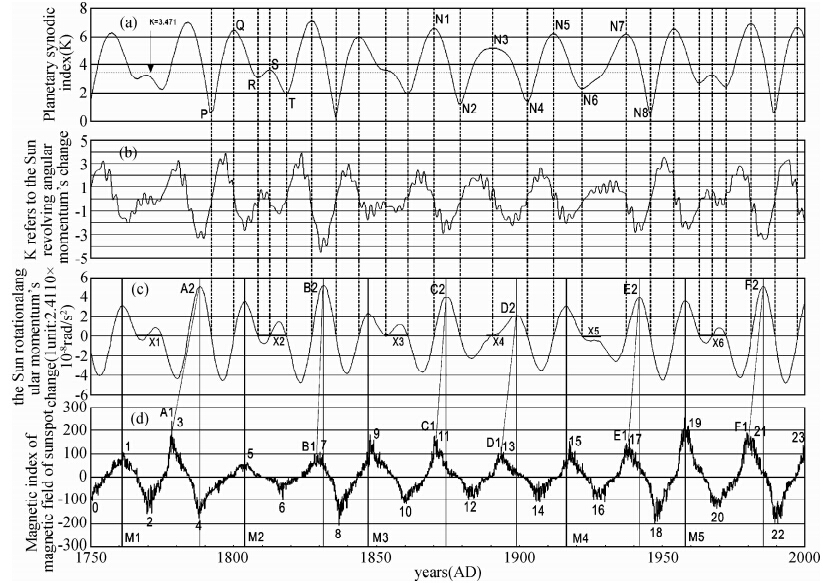 | 图 4 太阳轨道运动周期(a)、太阳轨道运动角动量变化周期(b)、太阳自转角动量变化周期(c)和太阳黑子磁场极性22年周期(d)的图像对比 Fig. 4 Comparisons of the cycle of the Sun’s orbital motion(a),the angular momentum variation of the Sun’s orbital motion(b),the angular momentum variation of the Sun’s rotation(c), and the 22-year cycle of the Sunspot magnetic index(d) |
因为木星、土星、海王星和天王星的轨道平面与不动面的夹角分别是0°23′、0°57′、0°46′、1°06′(戴文赛,1979),根据精度要求,可以视为行星系质心在“不动面”内运动(即Z=0).因为太阳距太阳系质心的距离与行星系质心距太阳系质心距离成正比例关系.所以可以通过行星系质心P的坐标(X,Y)变化指代太阳绕转角动量变化.根据
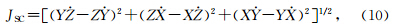
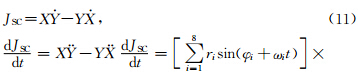
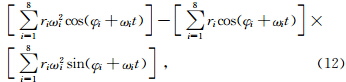
3 太阳活动双世纪周期和2403年哈尔斯塔周期
因为对太阳黑子的观测资料不超过400年,由此获得的周期长度一般不超过250年.更长的周期只能通过太阳活动替代性指标,或是通过这些替代性指标重建太阳活动的理论模型推测得到.到目前为止尚未发现从太阳活动可能的物理机制(dJS/dt或dω/dt)上获得超过双世纪长度的周期.刘复刚和王建等(2013a)在分析太阳轨道运动的双世纪周期和2400年哈尔斯塔周期时得出,前者是由平均9个19.8585年基本轨道运动周期集合而成,如图 2中峰值或谷值所呈现的周期.后者是由13~14个178~179年周期集合而成(两者均没改正).图 5b是将图 4a整个时间跨度延长到3万年,从而得到十分明显和稳定的2400年哈尔斯塔周期.从该周期峰值振幅相等的特点看具有十分稳定的等齐性,从周期长度看具有稳定的等长性.
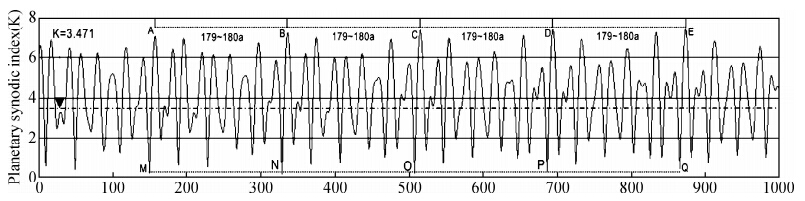 | 图 2 行星系统质心绕日不动点运动轨迹图像(纵坐标为行星会合指数K,原点为2000年,横坐标为过去距2000年的时间间隔)(该图像特征亦为太阳绕太阳系质心绕转的运动轨迹图像.但横坐标时间步长为1.0987年(此为改正系数,见刘复刚和王建(2013b)的证明);其纵坐标放大了746.153倍.太阳系质心绕太阳质心绕转的运动轨迹图像与图 2同形.K=3.471是太阳系质心进入和旋出太阳本体的临界值) Fig. 2 The path of planetary system centroid orbiting the Sun(vertical coordinate represents K,the origin represents the year of 2000, and the horizontal coordinate represents the time span from the past to the year of 2000AD)(The image also describes the path of the Sun orbiting the mass centre of the solar system. but horizontal coordinate the time unit was 1.0987-year(It is corrected factor; see reference Liu fugang and Wang jian(2013b)). The vertical coordinate enlarged 746.153 times. The image for the path of solar system mass center orbiting the Sun is similar to Fig. 2. K=3.471 is the boundary value for the mass center of the solar system entering into the Sun body.) |
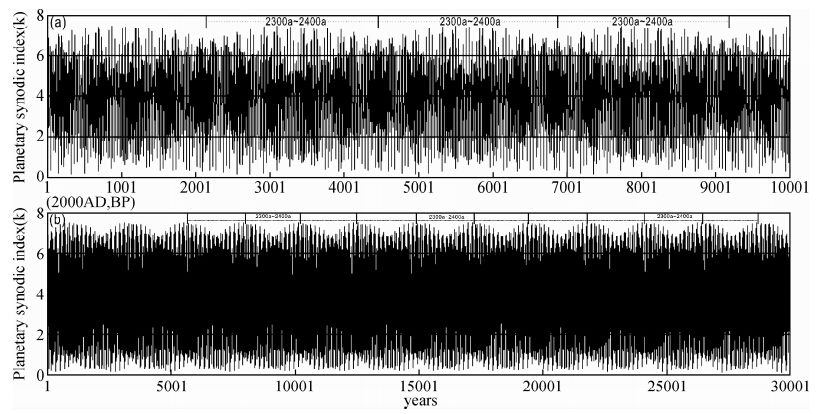 | 图 5 不同时间跨度太阳轨道运动双世纪周期和哈尔斯塔周期特征(未改正) Fig. 5 The double-century and Hallstatt cycles of the Sun’s orbital motion for different time scales(unrevised) |
图 6是将图 4c整个时间跨度分别延长到1万年和3万年,从该周期峰值的振幅和周期长度看具有与图 5一样稳定的等齐性和等长性.这说明太阳自转角动量变化和自转角速度同样具有双世纪周期和哈尔斯塔周期特点.同样可以用K指数指代的太阳自转角速度变化(dω/dt)规律与太阳活动替代性指标检测到的哈尔斯塔周期进行对比.这说明dω/dt可能是太阳活动超长周期性变化的成因,它可作为检验太阳活动替代性指标指代太阳活动周期律的理论时标依据,进而可以揭示区域性环境周期性变化的特点.由于太阳轨道运动和太阳自转角速度变化从图像振幅和周期长度看具有稳定的等齐性和等长性,同时二者又具有2400年周期,为此把2400年的哈尔斯塔(Hallstatt)周期称为太阳轨道运动和太阳活动的特征周期.
把太阳轨道运动角动量变化的图 4b同样延长到上述2种时间长度就没有发现如此明显的哈尔斯塔周期.图 7具有约2500年和5000年并存的特点,哈尔斯塔周期没有图 5和图 6明显,有的时段5000年周期更强(如2000~7000a;7000~12000a).
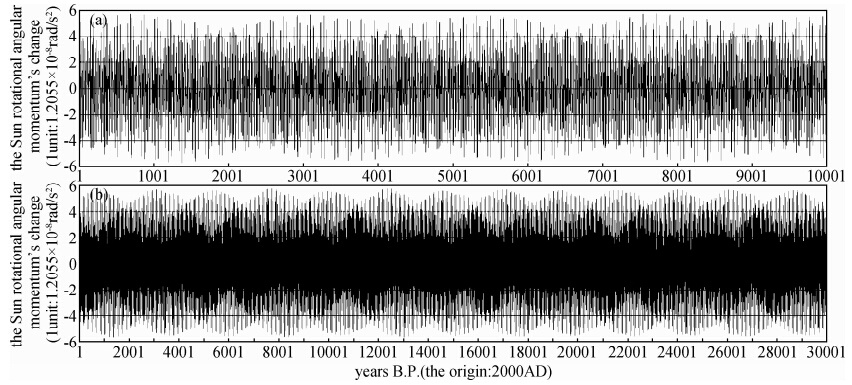 | 图 6 不同时间跨度太阳自转角动量变化双世纪周期和哈尔斯塔周期特征(未改正) Fig. 6 The double-century and Hallstatt cycles of the angular momentum variation of the Sun’s rotation for different time scales(unrevised) |
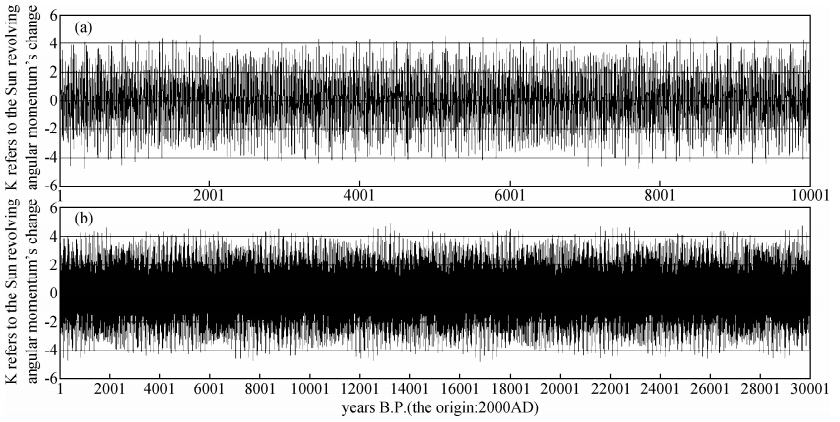 | 图 7 不同时间跨度太阳轨道角动量变化双世纪周期和哈尔斯塔周期特征(未改正) Fig. 7 The double-century and Hallstatt cycles of the angular momentum variation of the Sun’s orbital motion for different time scales(unrevised) |
太阳黑子活动的11年周期与太阳轨道运动的对应关系图见刘复刚和王建(2013b)文中图 11.偶数周对应K指数极小值,奇数周对应K指数极大值.因为K指数间接指代太阳轨道运动角动量的大小,虽然二者具有较好的相关性,但用K值大小指代太阳黑子活动在理论上还不能给出合理的解释.
太阳黑子磁极性指数变化除与太阳轨道运动具有较好的对应关系外,还具有太阳黑子磁极性指数极小值与太阳系质心进入太阳本体时K=3.471位置基本对应.这一时期刚好是太阳绕转角动量和太阳自转角动量进行交换的时期,说明此时期处于太阳活动的极值状态的解释近似合理.
太阳自转速度与太阳轨道运动特征K指数具有量值反向的一致对应关系(刘复刚和王建等,2013c),见本文中的图 3所示.太阳自转速度快似乎可以说明应对应太阳活动的极大值,因为按太阳表层磁力线的缠绕方式,太阳自转加速可以导致太阳的较差自转加速并产生磁力线扭结,致使磁力线缠绕程度加强(M.L.库特纳,2005).但不能很好说明太阳自转减速达到最大值时为什么也对应太阳黑子活动的极大值状态.
Jose(1965)和杨志根、赵铭(2012)给出了太阳轨道角动量变化图像与太阳黑子磁极性指数22年周期图像的对应关系.虽然二者具有较好的对应关系,然而,所有的太阳活动都是产生于或依附于太阳本体,所以从太阳轨道运动来阐述太阳活动的成因显然缺乏有说服力的动力学解释.
因为太阳自转和太阳绕太阳系质心绕转的角动量之和守恒,根据(12)式得到了太阳轨道运动角动量变化 (dJSC/dt)图像,如图 4b.这样就建立了图 4中的4种图像特征对比关系((a)、(b)、(c)图横坐标皆进行了改正).图 4中(a)图K指数峰值和谷值都具有平均19.8585年的周期(改正后为准22年).除此之外,K的极大值具有指代8大行星会合和相背离的极值程度.当K越接近Kmax=7.51时,说明行星会合在太阳一侧,近似排成直列的程度越高;当K越接近最小值Kmin=0时,则说明木星和其它7颗行星相背离的程度越大.理论上,行星系质心(P)与太阳质心(C)重合,也就是P、S和太阳系质心(C)三者重合,因为C始终位于P和S的连线上.因此K指数的变化揭示了整个太阳系结构是有规律变化的事实,即整个太阳系的质量分布相对太阳系质心(C)是变化的.
图 4b和图 4c呈现出量值反向的一致对应关系,这正是太阳自转角动量和太阳轨道角动量二者之和守恒的反映.图 4中(a)、(b)、(c)三图中的虚线具有特殊意义,图 4a P点处的虚线指示行星系质心(P)向太阳质心靠近,即C越接近S时候,K指数约等于0.该虚线在图 4b和图 4c中分别对应绕转角动量变化dJSC/dt=0和自转角速度变化dω/dt=0.因(c)曲线本身就是角速度变化曲线,且在A2竖线右侧dω/dt曲线是减函数,说明自转角速度ω的二阶导数小于零,所以虚线和纵坐标等0的交点处的角速度ω具有极大值.以同样 方法得到图 4a Q点虚线在图 4c与纵坐标值为0直线的交点处角速度ω具有极小值.同理R、S、T处也存在准确的对应关系,这说明按上述公式得到的图像形态特征是正确的.
如果将图 4c整个时间跨度延长到800年,如图 8.发现太阳角速度变化图像与太阳轨道运动图像一样也具有由9个约20年基本周期(振幅小于2的不计)集合成的178~179年周期,改正后为196~197年的双世纪周期.
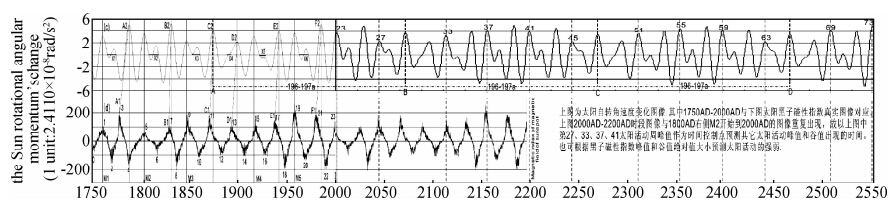 | 图 8 根据太阳自转角速度变化预测太阳活动周峰值的周期和强度 Fig. 8 Prediction of phase and degree of the solar activity cycle according to the changes of the angular momentum of the Sun’s rotation |
图 8c和图 8d左侧是图 4c和图 4d的太阳活动周和太阳自转角度变化周期,能在197年(从第1周到第19周)的双世纪周期中找到一一对应关系.如1、5、9、15、19周太阳活动黑子磁极性指数峰值与太阳自转角动量变化的极大值都有准确对应关系(如M1、M2、M3、M4、M5处所示).但图 8c谷值,即太阳自转角动量变化的极小值(绝对值仍然是变化的极大值)与太阳活动的偶数周(磁极性指数为负值的峰值)对应关系多数不吻合.但它们之间存在很好的规律性:如果太阳自转角动量变化从振幅最大的极大值向振幅最小值的极小值转变时,出现波动.如图中X1、X2、X3、X4、X5、X6处,则太阳活动偶数周峰值(负的绝对值大)提前于太阳自转角动量变化的极小值,这可能是处于太阳系质心C进入太阳本体时绕转角动量和自转角动量转换产生波动造成强太阳活动提前所致.这也导致了接下来的奇数周也提前于太阳角速度变化的极大峰值,如A1-A2、B1-B2、C1-C2、D1-D2、E1-E2、F1-F2所示.而上述1、5、9、15、19太阳活动周期峰值的准确对应则是dω/dt由振幅极大值向振幅极小值转变,和接下来由极小值向极大值转变时都没有发生波动的体现.这说明当太阳系质心(C)按一种曲率稳定地旋进和旋出太阳本体时,接下来就有一个准确的太阳活动奇数周与太阳角速度变化dω/dt极大值准确对应.
根据系统结构决定系统功能的观点,太阳自转角速度变化(dω/dt)的结构特点,应该与太阳活动变化特点相关联并对其产生影响.因此可以通过dω/dt图像确定相应的太阳黑子活动极值状态所对应的时间,以此来预测太阳活动奇数周和偶数周何时到来以及强弱的变化.图 8中2000AD之后的长竖虚线给出了太阳活动奇数周的准确对应时间(见表 2),以此为时间控制点可以推断其它峰值和谷值的时间.其强弱可比照2000AD之前的对应关系作出判断.例如,介于第23周和第25周之间的第24周对应的太阳自转角速度变化图像与第5周和第7周所对应的图像是同构的,所以推断第24周太阳活动强度与第6周基本一致,应是太阳活动较弱周,其峰值在2013年初到来,这情况已得到了证实(Chernosky,1966; Qian, et al., 2006; Jiang, et al., 2007; Antia and Basu, 2013).
5 结 论5.1 基于K指数运动学方程,推导出太阳自转角动量与太阳绕转角动量之和守恒.进而得到太阳自转角动量变化(dJS/dt)与K指数的函数关系,发现dω/dt=0与太阳轨道运动图像中K的极值准确对应,并能给出合理解释.
5.2 太阳活动的双世纪周期和Hallstatt周期可由太阳角速度变化的22年准周期集合而成.这说明由22年dω/dt周期在长时间尺度指代太阳活动规律更具有合理性.在图4中的(c)图和(d)图中,在一个完整的双世纪周期(197年)中有4处dω/dt峰值与太阳黑子磁极性指数峰值准确对应.由于dω/dt结构变化具有稳定的197年周期,且在该周期内能找到准确的4个太阳活动峰值的时间控制点,因此可以通过这种对应关系预测未来太阳黑子活动的周期和强弱变化的规律.其它峰值和谷值在上述时间控制点的基础上也可以给出基本预测.
5.3 太阳轨道运动和太阳自转角速度变化具有稳定的Hallstatt特征周期.它们都是由最基本的22周期集合而成,而这种22年周期的峰值和太阳活动奇数周的峰值对应,谷值和太阳活动偶数周一一对应.而峰值对应太阳黑子磁极性指数的极大值,谷值对太阳黑子磁极性指数的极小值,这说明Hallstatt周期的峰值也是由太阳黑子磁极性指数极大值构成,因此可以推断太阳活动的Hallstatt长周期也应该是太阳活动在千年尺度上的磁周期.
| [1] | Antia H M, Basu S. 2013. Contrasting the solar rotation rate of cycles 23 and 24[J]. J. Phys.: Conf. Ser., 440(1): 012018. |
| [2] | Charvátová I. 2009. Long-term predictive assessments of solar and geomagnetic activities made on the basis of the close similarity between the solar inertial motions in the intervals 1840-1905 and 1980-2045[J]. New Astronomy, 14(1): 25-30. |
| [3] | Chernosky E J. 1966. Double sunspot-cycle variation in terrestrial magnetic activity, 1884-1963[J]. Journal Geographic Reserch, 71(3): 965-974. |
| [4] | de Jager C. 2008. Solar activity and its influence on climate[J]. Netherlands Journal of Geosciences-Geologie en Mijnbouw, 87-3: 207-213. |
| [5] | Foukal P. 1998. Extension of the F10.7 index to 1905 using Mt. Wilson Ca K spectroheliograms[J]. Geophysical Research Letters, 25(15): 2909-2912. |
| [6] | Haigh J D. 2007. The Sun and the Earth's Climate[J]. Living Rev. Solar Phys.,4, doi: 10.12942/lrsp-2007-2. |
| [7] | Jiang J, Chatterjee P, Choudhuri A R. 2007. Solar activity forecast with a dynamo model[J]. Monthly Notices of the Royal Astronomical Society, 381(4): 1527-1542. |
| [8] | Jose P D. 1965. Sun's motion and sunspots[J]. The Astronomical Journal, 70(3): 193-200. |
| [9] | Kane R P. 2002. Some implications using the group sunspot number reconstruction[J]. Solar Physics., 205(2): 383-401. |
| [10] | Krivova N A, Vieira L E A, Solanki S K. 2010. Reconstruction of solar spectral irradiance since the Maunder minimum[J]. Journal of Geophysical Research, 115(A12): A12112. |
| [11] | Le GM, Wang J L. 2004. Wavelet analysis of the strongest periods in the relative sunspot numbers[J]. Chinese J. Geophys. (in Chinese), 47(5): 743-746. |
| [12] | Lean J. 1987. Solar ultraviolet irradiance variations: A review[J]. Journal of Geophysical Research: Atmospheres (1984-2012), 92(D1): 839-868. |
| [13] | Lean J. 1997. The Sun's variable radiation and its relevance for earth[J]. Annu. Rev. Astron. Astrophys., 35: 33-67. |
| [14] | Liu F G, Wang J. 2013b. Changes of the planet juncture index and solar revolution cycle around the mass center of the solar system[J]. Chinese J. Geophys. (in Chinese), 56(5): 1457-1466, doi:10.6038/cjg20130504. |
| [15] | Liu F G, Wang J, Shang Z Y, et al. 2013a. Study on long-term cyclical rhythm of solar activity[J]. Chinese Journal of progress in Geophysics (in Chinese), 28(2): 570-578, doi:10.6038/pg20130205. |
| [16] | Liu F G, Wang J, Bai S B, et al. 2013c. The planetary motion and the change of 22-year cycle of the Sun spin velocity[J]. Progress in Geophys. (in Chinese), 28(4): 1678-1683, doi:10.6038/pg20130406. |
| [17] | Qian L Y, Roble R G, Solomon S C, et al. 2006. Calculated and observed climate change in the thermosphere, and a prediction for solar cycle 24[J]. Geophysical Research Letters, 33(23): L23705.1-L23705.5. |
| [18] | Qu W Z, Deng S G, Huang F, et al. 2004. Influence of magnetic index abnormal change in the solar magnetic field on climate at the middle latitudes of north hemisphere[J]. Chinese J. Geophys. (in Chinese), 47(3): 398-405 |
| [19] | Qu W Z, Qin T, Deng S G, et al. 2008. The time sequence of the magnetic index of the sunspot magnetic field[J]. Progress in Geophysics, 23(6): 1727-1735. |
| [20] | Scafetta N. 2012. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass-luminosity relation[J]. Journal of Atmospheric and Solar-Terrestrial Physics., 81-82: 27-40. |
| [21] | Schrijver C J, Livingston W C, Woods T N, et al. 2011. The minimal solar activity in 2008-2009 and its implications for long-term climate modeling[J]. Geophysical Research Letters, 38(6): L06701. |
| [22] | Solanki S K, Fligge M. 1998. Solar irradiance since 1874 revisited[J]. Geophysical Research Letters, 25(3): 341-344. |
| [23] | Ternullo M. 2007. The butterfly diagram fine structure. Solar Phys., 240(1): 153-164. |
| [24] | Yang Z G, Zhao M. 1988. An investigation for the cause of formation of the major period of the relative sunspot numbers with bipolarity[J]. Acta Astronomica Sinica (in Chinese), 29(3): 297-304. |
| [25] | Yang Z G. 1991. The possible influence of the orbital motion of the major planets on sunspot activities[J]. Chinese Journal of Astronomy and Astrophysics, 11(4): 370-377. |
| [26] | Zolotova N V, Ponyavin D I, Marwan N, et al. 2009. Long-term asymmetry in the wings of the butterfly diagram[J]. Astronomy & Astrophysics, 503: 197-201. |
| [27] | 陈彪, 印春霖. 1965. 关于太阳活动周期—相对数曲线的一种数学表达式[J]. 天文学报, 13(1): 89-96. |
| [28] | 戴文赛. 1979. 太阳系演化学(上册)[M]. 上海科学技术出版社, 22-23. |
| [29] | 郭汉伟, 乐贵明. 2004. 太阳黑子群周期的小波分析[J]. 自然科学进展, 14(5): 597-600. |
| [30] | 库特纳 M L. 2005. 天文学: 物理学新视野[M]. 萧耐园, 胡方浩译. 长沙: 湖南科学技术出版社. |
| [31] | 乐贵明, 王家龙. 2004. 太阳黑子相对数最强周期的小波分析[J]. 地球物理学报, 47(5): 743-746. |
| [32] | 李可军, 苏同卫, 梁红飞. 2004. 现代黑子观测的太阳黑子活动的周期性[J]. 科学通报, 49(24): 2511-2516. |
| [33] | 李可军, 冯雯, 梁红飞. 2010. 异常的第 24 太阳活动周—新千年的第一个完整的太阳活动周[J]. 中国科学: 物理学 力学 天文学, 40(10): 1293-1301. |
| [34] | 李政道, 朱允伦, 柳怀祖. 2000. 对称与不对称[M]. 清华大学出版社、暨南大学出版社. |
| [35] | 廖德春 廖新浩. 2001. 太阳活动影响地球自转长周期变化的新证据[J]. 科学通报, 44(1): 13-16. |
| [36] | 刘复刚, 王建. 2013b. 行星会合指数变化与太阳绕太阳系质心运转的周期[J]. 地球物理学报, 56(5): 1457-1466, doi:10.6038/cjg20130504. |
| [37] | 刘复刚, 王建, 商志远,等. 2013a. 太阳轨道运动长周期性韵律的成因[J]. 地球物理学进展, 28(2): 570-578, doi:10.6038/pg20130205. |
| [38] | 刘复刚, 王建, 白世彪,等. 2013c. 行星运动与太阳自转角速度22年周期变化[J]. 地球物理学进展, 28(4): 1678-1683, doi:10.6038/pg20130406. |
| [39] | 尹志强, 马利华, 韩延本,等. 2007. 太阳活动的甚长周期性变化[J]. 科学通报, 52(16): 1859-1863. |
| [40] | 占腊生, 何娟美, 叶艺林,等. 2006. 太阳活动周期的小波分析[J]. 天文学报, 47(2): 166-174. |
| [41] | 张桂清. 2003. 太阳活动周期变化与日地关系[J]. 大自然, (4): 29-31. |
| [42] | 赵铭. 2012. 天体测量学导论(第2版)[M]. 北京: 中国科学技术出版社, 357-357. |
| [43] | 周衍柏. 1986. 理论力学教程(第2版)[M]. 北京: 高等教育出版社, 14, 64, 112-114. |
 2014, Vol. 29
2014, Vol. 29