2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
深层地热资源具有资源量巨大、污染零排放、安全性好、热能连续性好、利用效率高、发电成本低等优点(王晓星等,2012).而增强型地热系统(Enhanced Geothermal System,简称EGS)目前被认为是深层地热资源开采的最有效技术.建造EGS电站,首先需钻井至适当深度,通过注入高压流体,实现水力压裂,增强特定区块的岩体导流能力,形成可用的人造储层,然后再钻井穿过人造裂隙网络,实现井孔间的裂隙连通.通过流体在注入井、生产井及人造裂隙系统中循环提取干热岩中的热量,获得的高温热液带到地表,再进行能量转化或直接利用(Abé, et al., 1999;Brown, et al., 1999;苏正等,2012).
EGS运行中,始终存在多个物理化学场的耦合作用(王晓星等,2012).了解ESG的运行状况和储层特征的变化,必须对其中的多场耦合过程有清晰认识.当然,在EGS开发过程中,并不是所有场之间的耦合都必须考虑,如力-热耦合、化-热耦合都可忽略不计(王晓星等,2012).由于EGS开发以裂隙建造为核心,无论是前期流体与岩石之间短期快速的激发作用,还是后期深部复杂地质环境流体循环长达数年甚至数十年的运行过程,与力学作用有关的诸多变化因素往往都是影响裂隙产生和生长的主要原因,进而影响流水路径以及热储换热性能.因此,当前对EGS多场耦合的研究大多集中在热-流-力(T-H-M)三场耦合上(Mclarty, et al., 2000;Sanyal, et al., 2000;赵阳升等,2004;MIT,2007).
在T-H-M耦合中,由于力学影响的存在,导致耦合的强非线性,在处理耦合计算时或是弱化热流的作用,或是复杂化热流的作用.导致的结果都是对最基本的热流耦合过程认识不深刻,从而无法从本质上认识裂隙中的热开采过程.事实上,EGS开发的主要目标是在裂隙储层内,流体与岩体充分接触的前提下,生产井保持较高流体温度和流量的同时确保足够长的储层寿命,这本质上是一个流动传热问题.因此,从EGS初期研究探索和储层产热效率分析角度看,EGS多场耦合中最基本和最重要的耦合关系应为热流耦合(T-H耦合),即在温度场作用下裂隙介质的渗流问题.
目前已有学者对热流耦合进行了初步的数值模拟研究(He, et al., 2010;Shaik, et al., 2011;Gelet, et al., 2012;Chen, et al., 2013;Jiang, et al., 2013),但是单纯的数值模拟研究既不能保证其模拟过程的合理性,也无法从本质上对问题产生深刻认识,更无法对影响问题的因素进行有导向的敏感性分析.而且已建模型在处理耦合过程中传热量时大部分都是以水与裂隙面对流换热系数为基础来近似考虑的(He, et al., 2010;Shaik, et al., 2011;Gelet, et al., 2012;Chen, et al., 2013;Jiang, et al., 2013).然而,对流换热系数不是一个热物性参数,其取值受环境的影响较大,不同模拟条件下取值差别往往较大,这也在较大程度上影响了预测效果.而特定岩体的热传导系数是一个热物性参数,其值不易受到模拟条件变动的影响,以岩体热传导系数为基础来考虑耦合过程中的传热量,有利于更精确地模拟计算不同条件下的热流耦合过程.
为深入认识EGS运行中热流耦合过程,从理论上刻画热从岩体传导至裂隙面和裂隙流体,以及热量被提取的过程,需要建立一个专门针对热流耦合过程的简明数学模型.本文研究中建立了基于岩石热导系数表征的水岩耦合传热模型,并基于该模型求解出对应的水岩耦合温度场解析解,重建热在岩体和裂隙中的传递过程,研究水岩温度场与裂隙长度、裂隙宽度、水流速度等之间的关系,分析裂隙特征对采热效率的影响.
1 概念模型
EGS热储是由高温岩石块体和裂隙网络组成的裂块结构.对于采用怎样的几何形态抽象热储结构用于研究热提取过程,前人已有很多探索(Gringarten, et al., 1975;Mcfarl and , et al., 1976;Wunder, et al., 1978;Cheng, et al., 2001).尽管实际情况中,热储中裂隙肯定是由多条复杂的裂隙组成,但是有研究表明单裂隙模型已经能捕捉多复杂裂隙系统中EGS热提取的基本特征和过程(Cheng, et al., 2001).即便是裂隙中流体经历了复杂的流动路径,但最终由注入井流向产出井,所采热量都源于裂隙两侧的热岩体,单裂隙流犹如把一个复杂曲折的流动路径拉直,更易于从机理上认识EGS裂隙储层中热流耦合作用和温度场特征.
本文在借鉴前人经验基础上建立了单裂隙概念模型,如图 1所示,岩体中间仅有一条裂隙,岩体被单裂隙分开为两部分.干热岩体的初始温度为Tr0,裂隙宽度为δ,长度为L,注水温度为Tf0,以匀速uf流入裂隙,在流经裂隙过程中与两侧的高温干热岩发生热交换,流体温度场Tf和岩体温度场Tr将不断变化.水岩交界处的热传导量为2Q,垂直于裂隙水流方向.设置二维坐标x-z轴.入口处为(0,0)点,沿裂隙向上为z正方向,垂直z方向和视角界面向右为x正方向.与裂隙垂直的水平方向x可无限延伸.系统运行时水从(0,0)处进入裂隙系统,从(0,L)处离开裂隙系统,并提取热能.
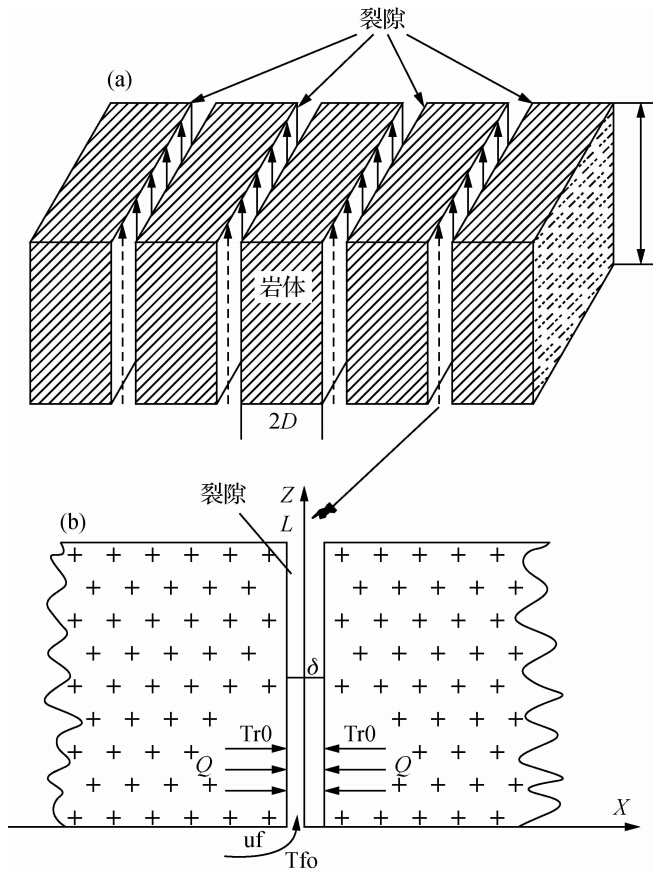 | 图 1 单裂隙流动采热概念模型(a)整体三维立体模型;(b)局部二维平面模型.δ和L分别表示裂隙宽度和长度、Tr0是岩体原始温度、Tf0是进水温度、uf是水流速率、2D是两裂隙间的间距.低温流体的注入和流动,必然引起流体温度上升、热干岩温度下降.Q表示裂隙界面处的热交换量.Fig. 1 Conceptual model of flow and heat production in single fracture(a)The 3D view conceptual model;(b)The local 2D plane model.δ and L respectively denote width and length of the fracture,Tr0 represents original temperature of the matrix,Tf0 represents temperature of the inlet fluids,uf represents velocity of the inlet fluids, and 2D represents the spacing in between fractures . Injection and flow of low-temperature fluid must induce increases in fluid temperature and decreases in rock temperature. Q represents the amount of heat exchange at the interface of fracture. |
为简化问题,提取问题本质特性,对研究对象作如下假设:
1 )岩体是均质各向同性的不渗透块体,无岩体孔隙流体产出.在低孔渗条件下,该假设被近似认为可靠.
2)岩体热传导系数较低,水岩交界处热阻忽略,即裂隙面上流体温度与岩体温度相等.这一假设的合理性已经在很多已有的实际案例中得到证实(Mcfarl and ,et al.,1976;Wunder,et al.,1978;Ogino,et al.,1999;Fox, et al., 2013).
3 )裂隙中水流方向为单向,且速度均匀.
4)裂隙流体温度变化只表现在水流方向.这是因为裂隙宽度很小,即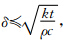 热效应在x方向的影响很小.
热效应在x方向的影响很小.
5 )沿z方向的热传导忽略不计.只考虑岩体中沿x方向的热传导及裂隙流体中沿z方向的热对流.这一假设是基于在热开采过程中,x方向温度梯度远大于z方向温度梯度以及裂隙宽度一般很小这一事实.
6)热辐射效应一律不予考虑.这一点已由实验证明可信(田鲁鲁,2003).
7 )裂隙水中温度增量为单边水岩传热效应的两倍(陈兴周等,2007).这由系统对称性导致.
8)系统运行时裂隙水始终为液相.
9 )热开采阶段不考虑热恢复效应(Fox, et al., 2013).
10)忽略温压条件变化对系统热物性的影响,即整个热开采过程中岩体的热传导系数、比热容、密度为常数,裂隙水的比热容、密度为常数.
2 数学模型
根据传热学理论及概念模型中的假设,可知裂隙流体温度场控制方程包含非定常项、对流项及源项;高温岩体温度场控制方程只包含非定常项和热传导项.
推导过程中,系统的温度场统一用T表示,其中岩体温度场与裂隙流体温度场分别用下标r和下标f区分.由假设2、3、4可知,岩体温度场是x、z和t的函数,裂隙流体温度场是z和t的函数.分别得到水岩温度场的控制方程.
裂隙流体温度场控制方程为
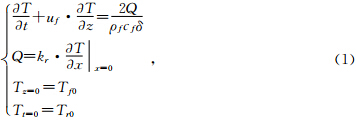
岩体温度场控制方程为
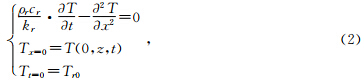
对上述耦合数学模型采用拉普拉斯变换法求解(严震军,2004;胡汉平,2010),可变为
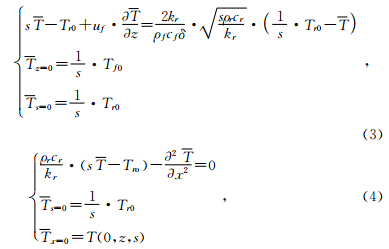
基于上述耦合方程特征,先求解带有未知量的岩体温度场,后利用岩体温度场将体现模型耦合作用的Q表达出来,再代入到裂隙流体温度场方程中,运用无量纲化、拉普拉斯变换、平移定理及反拉普拉斯变换耦合求解,最后得到热流耦合水岩温度场数学模型解析解.
岩体温度场:
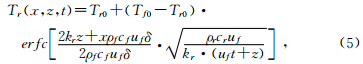
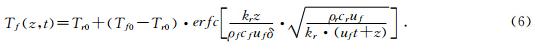
从上述解析模型中可以看出岩体温度场和流体温度场都与岩体初始温度Tr0和注水温度Tf0有关,不同空间位置上的温度变化是裂隙宽度δ、水流速率uf和时间t的函数.
3 计 算
EGS工程主要是在深层高温花岗岩和花岗闪长岩类的岩石中实施.从数学解析模型可以看出,岩体初始温度、裂隙宽度和长度、注水温度、水流速度等对系统温度场变化和热能提取效率、系统寿命、工程的经济性等有关键性影响.本文计算中对上述影响因素的参考取值借鉴前人所做研究时取值水平(Shaik, et al., 2011).具体相关参数见表 1.
|
|
表 1 模型计算相关参数参考值 Table 1 Reference value of the parameters in the modeling |
EGS开发的主要目的是通过流体在地下热储层中的循环,从裂隙岩体中提取地热能,其基本要求是能从开采井中源源不断地产出足量的高温水,因此,裂隙水升温过程和产水温度是衡量EGS储层开发效益和寿命的关键指标.图 2表征了在参考参数条件下裂隙流体的温度场特征.流体温度从进水口(z=0)开始逐渐升高,并在流到出水口(z=1000)之前达到岩体初始温度.可以看出在热开采进行10年时,水沿裂隙流经500 m左右时,其温度即可上升到200 ℃的岩体初始温度,其后半程温度维持不变;在热开采进行20年时,水沿裂隙流经635 m时温度达到200 ℃;开采进行30年时 的升温路径长度为778 m,40年时的升温路径长度为878 m,50年时为992 m.
计算表明,在上述条件下的热开采过程中,裂隙出口的流体温度与岩体初始温度相等,即Tf=Tr0=200 ℃,可认为该单裂隙地热开采系统可以高效稳定运行.同时也说明当要求该地热系统高效运行10年、20年、30年、40年或50年,其 相应岩体裂隙长度最好分别达到500 m、635 m、778 m、878 m和992 m,才能保证循环水流被加热到岩体初始温度.若放宽评价指标,产水温度与岩体初始温度相差在10%以内,即最大温降为20 ℃,Tf≥180 ℃,运行10年所需的裂隙长度为230 m,而运行50年所需的裂隙长度为515 m.这说明 在此类EGS裂隙储层中,只要裂隙长度或水流路径达到515 m以 上,在设定的水流条件下,该系统可在运行50年内满足EGS开发的温度指标要求.
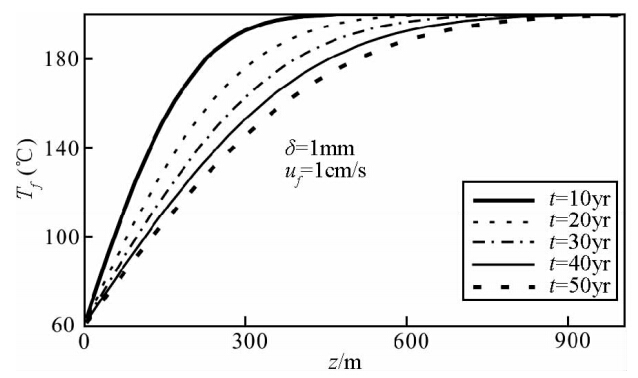 | 图 2 参考条件下裂隙流体的温度场特征及变化.裂隙宽度为1 mm,流水速率为1 cm/s.温度对比的时间点分别是开采进行了10年、20年、30年、40年和50年Fig. 2 Evolution characteristics of fracture fluid temperature field in the reference conditions. The fracture width is 1 mm,the flow rate of inlet fluids is 1 cm/s. The timing of temperature contrast is 10 yrs,20 yrs, 30 yrs,40 yrs, and 50 yrs,respectively |
地热能开采必然引起岩体温度下降,而岩体温度场特征及其变化规律反映了水岩热交换过程和可持续开发潜力.图 3表征了在参考参数条件下,干热岩单裂隙热开采过程中的岩体温度场在x-z平面展布特征和演化规律.可以看出,裂隙底端进水口处为明显低温区,随着开采年限的增加,在x方向上的采热半径(横向温度变化区间长度)逐渐增加,在z方向上的采热区间(纵向温度变化区间长度)逐渐拉长,但岩体温度逐渐接近岩体初始温度,形成了逐渐扩张的三角形采热区域,热开采的影响面积不断增大.
在EGS开发运行中,如果岩体温度下降超过10%,预示着储层产热效率不足,系统需要终止运行或暂歇以使温度恢复,因此,以温度下降超过20 ℃,即Tr≤180 ℃为界划定单裂隙系统热开采的严重影响区域,有助于分析储层潜力和出力寿命等.如图 3显示,热开采进行10年对x、z方向上温度的显著影响长度分别为34 m和230 m;开采20年在x、z方向上的显著温度影响长度分别为47 m和325 m;30年的显著温度影响长度分别为58 m和400 m;开采40年的显著温度影响长度分别68 m和460 m,影响面积约为3.1万m2.也就是说,在参考裂隙宽度和水流速率条件下,40年的采热作业后,注入井所在平面周围约3.1万m2岩体温度需要恢复.
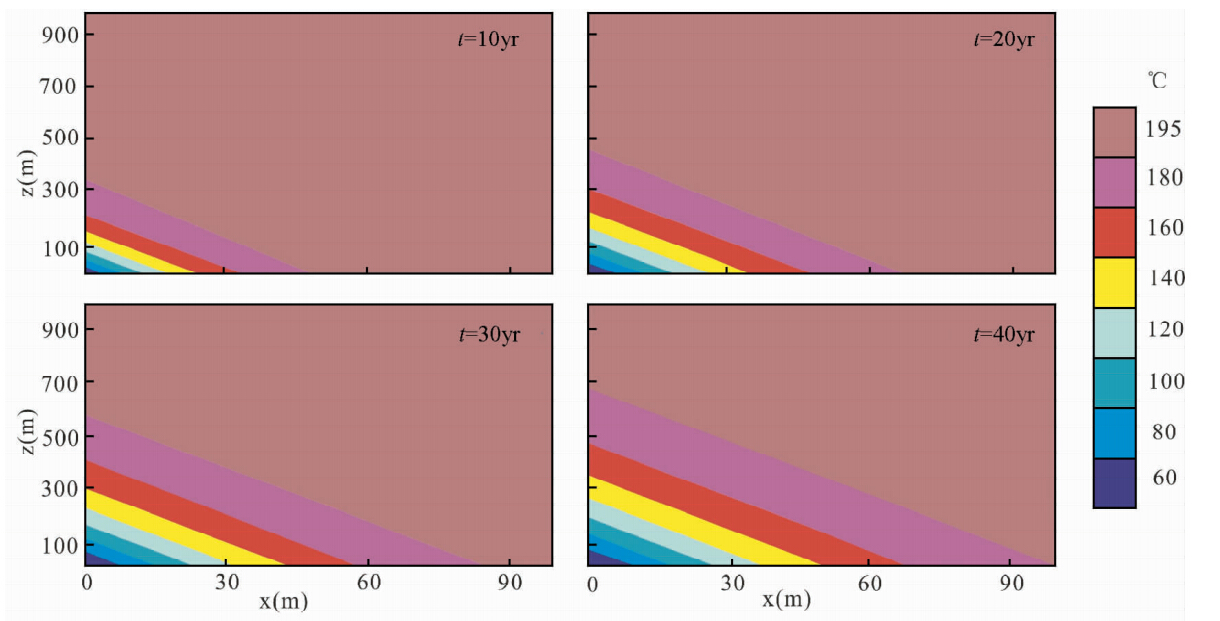 | 图 3 参考条件下模拟的热开采过程中岩体温度场演化特征.裂隙宽度为1 mm,水流速率为1 cm/s.显示的温度场时间点分别为10年、20年、30年和40年Fig. 3 Evolution of the matrix temperature field in simulated heat mining process under the reference conditions. The fracture width is 1 mm,the flow rate of inlet fluids is 1 cm/s. The timing of temperature contrast is 10 yrs,20 yrs,30 yrs, and 40 yrs,respectively |
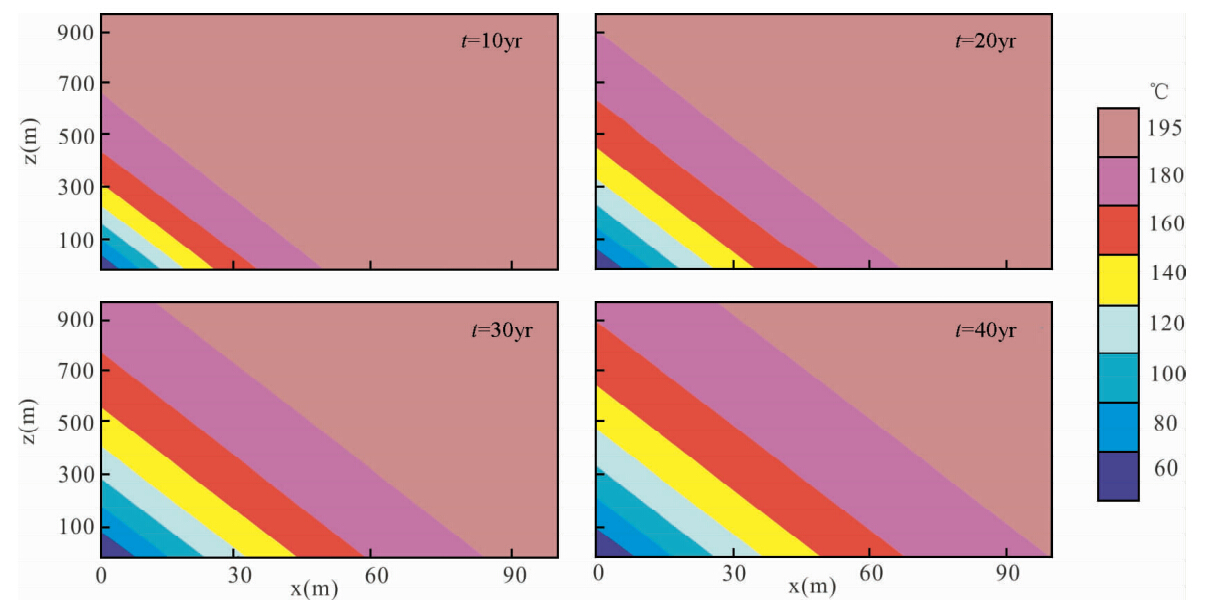 | 图 5 裂隙宽度为2 mm时热开采过程中岩体温度场演化特征.水流速率为1 cm/s.显示温度场时间点分别为10年、20年、30年和40年Fig. 5 Evolution of temperature field in the matrix rock during heat mining process. The flow rate of inlet fluids is 1 cm/s. The timing of temperature field is 10 yrs,20 yrs,30 yrs, and 40 yrs,respectively |
裂隙主要是由储层建造过程中的水力压裂所致,裂隙宽度决定于岩石性质和水力压裂工艺技术、以及后期流体循环作业过程中的裂隙发育控制技术.裂隙宽度与流体循环阻抗、水流短路、产热效率和储层寿命等问题密切相关.在水流速率等条件一定时,裂隙宽度决定了裂隙中的进水量和含水量及对岩体热量的提取能力,同时还决定了流体加热到特定温度需要的加热时间、热量和裂隙路径长度等,从数学解析模型中也可以看出,裂隙宽度与岩体温度下降存在正相关.
图 4显示了裂隙宽度对流体温度场的影响.相对于参考条件,仅把裂隙宽度变为原来的两倍(从1 mm变大为2 mm),其它条件不变,即裂隙长度约为1000 m、水流速率为1 cm/s、岩体初始温度为200 ℃、进水温度为60 ℃.在裂隙流体从进水口流向出水口过程中,其温度逐渐升高的规律仍然存在,但温度增长减缓,水温上升路径长度明显增大.从图中可以看出,热开采进行10年,水流温度在出水口附近才到达岩体初始温度,即其所途径的裂隙长度为1000 m,约为参考条件下水流加热路径长度(500 m)的两倍;热开采进行20年时,裂隙出口处的水流温度为197 ℃,略低于岩体初始温度;热开采进行30年、40年和50年时的产水温度分别为191 ℃、185 ℃、179 ℃.这说明,如果在系统运行期间,允许的最大产水温度降幅为20%,则此裂隙系统基本可以满足50年的开采强度,最终的产水温度约为179 ℃.
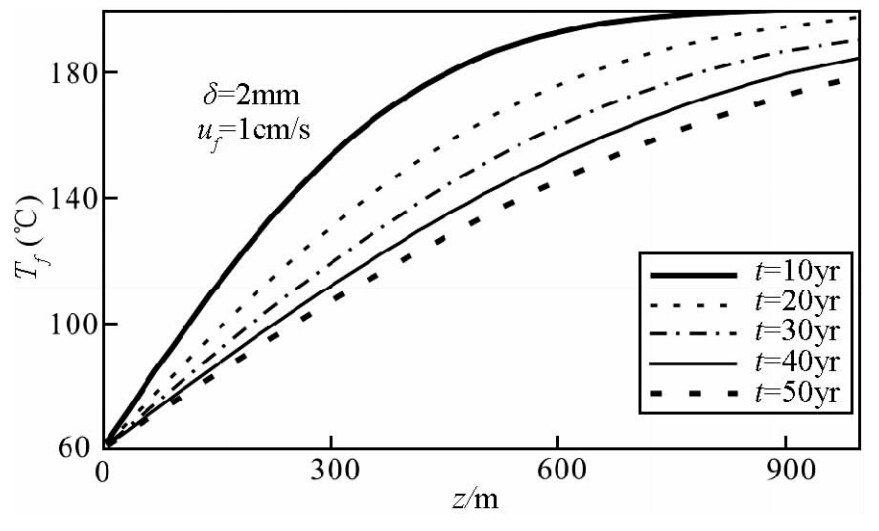 | 图 4 裂隙宽度对裂隙流体温度场的影响.裂隙宽度为2 mm,水流速率为1 cm/s.温度对比的时间点是开采进行10年、20年、30年、40年和50年Fig. 4 Effect of fracture width on the fracture fluid temperature. The fracture width is 2 mm,the flow rate of inlet fluid is 1cm/s. The time points for temperature contrast are respectively 10 yrs,20 yrs,30 yrs,40 yrs, and 50 yrs since the production get started |
裂隙宽度影响了水温的增长过程,也因此影响岩体热传输和温度场分布特征.图 5显示了裂隙宽度增加1倍后的岩体温度场分布和演化特征.相对于参考情形,仅把裂隙宽度从1 mm变大为2 mm,从岩体温度场在x-z平面上展布特征和演化规律可以看出,裂隙流体入口处仍为明显低温区,且表现为x方向采热半径逐渐增加、z方向采热区间逐渐拉长的特征.但与图 3比较发现,裂隙宽度增长1倍后,x方向上的采热半径几乎没有变化,而z方向上的采热区间有显著增长,热开采影响面积也明显变大.开采进行10年和20年时,z方向上采热区间分别为660 m和930 m,都明显大于参考条件下的采热区间,开采到第30年时,产水温度已低于岩体初始温度,裂隙流体从整个裂隙两侧的岩体采热.若以岩体最大温降20 ℃为储层稳定性能评价标准,即裂隙出口处的岩体温度低于180 ℃,则此裂隙系统的最大运行时间约为50年.
3.3 水流速率对水岩温度场的影响
从理论上分析,进入裂隙储层的水流通量正比于裂隙宽度和水流速率.在裂隙宽度等条件一定时,水流速率决定了裂隙水流通量和热量传输速率.裂隙内的热量对流传输速率取决于流体速度,当水流速率较快时,水尚未得到充分加热即已流出裂隙岩体,裂隙储层产水温度较低.从极端条件看,水流速率足够快时,裂隙水温度变化不大,产水温度甚至接近进水温度,即“短路”;热岩体与裂隙水之间的热量传输主要通过热传导实现,热传导速率取决于水岩之间的温度梯度,裂隙流体温度越低,其与热岩体之间的温度梯度越大,热传递效率越高,而裂隙流体温度与水流速率相关,因而,快速水流速率造成快速的热量传输和岩体温度下降,而且低温水流造成较长的采热区间.
从水岩温度场的数学解析模型可以看出,裂隙水流速率和裂隙宽度一样,与温度下降存在正相关,但水流速率与水岩温度场间的响应关系更为复杂.模拟计算中,裂隙水流速率增加1倍(从1 cm/s变为2 cm/s),而其它条件维持不变.计算结果表明,水流速率变化对水岩温度场演化特征的影响与同样倍数裂隙宽度变化产生的影响,即水流温度增长、岩体中的热影响半径、采热区间、采热面积几乎完全一致.这说明数学模型中根号内水流速率参数对水岩温度变化的贡献可以忽略不计,水流速率变化与裂隙宽度变化对水岩温度场的影响处于同等地位.
4 讨 论
本文EGS水岩温度场研究中,将热储内裂隙系统抽象为单裂隙形式,这与实际EGS热储的裂隙网络形态存在明显差异.但若以研究热储内部基本传热过程为目的,抽象为单裂隙已能捕捉复杂裂隙系统中热提取的基本特征(Cheng, et al., 2001).因此,应用此单裂隙模型,对EGS热储内部的传热过程和采热效率展开研究,具备代表性.
4.1 传热过程
EGS热开采过程中,岩体内部的热量传输包括热传导和热液对流,其中热液对流热量传输决定于岩体孔隙度、渗透率、热液饱和度和岩体的可压缩性,对一般的深部花岗结晶岩体,其孔渗条件很差,可压缩性很小,天然蕴含的热液很难在压力差作用下流向裂隙网络,因此,岩体内部的热量传输可视为通过热传导完成.
热量从温度较高的岩体内部传导至温度较低的岩体边界—裂隙面,高温岩石裂隙面与进入裂隙的低温水发生热交换,水岩接触瞬间,由于水岩温差巨大,热量传输较快,但水的热容较大,温度增长需要较多热量,因此,裂隙面温度被很快拉低至与水温相当.如果到达裂隙界面的热量都能瞬间被低温水吸收,即“平衡热交换”,则在水岩接触瞬间其温度差基本消失,水温等于与之接触的裂隙面温度(Mcfarl and , et al., 1976;Wunder, et al., 1978;Ogino, et al., 1999;Fox, et al., 2013).如果裂隙水不能与到达岩体边界的热量瞬间完成热交换,只吸取了其中部分热量,其温度不能与裂隙面达到平衡,仍存在一定的温度差,这种热交换量和温度差决定于二者的换热系数.
同时,需要指出的是,本文中处理水岩热交换时依然是基于局部热平衡(local thermal equilibrium)假设.但是Sanyal等人为,裂隙间距在2~3 m以上即不宜采用局部热平衡假设.为充分考虑岩石与流体之间的对流换热效应,采用基于局部非热平衡(local thermal non-equilibrium)思想应该是本模型今后工作的改进方向(Sanyal, et al., 2005;陈继良等,2013).
本模型耦合计算时处理岩体对流体加热效应是基于岩石的热传导系数,而文献8模型耦合计算时处理岩体对流体加热效应是基于流体在流过裂隙面时的对流换热系数.在与文献8使用相同基本参数的前提下,对比两种不同耦合模型计算结果中,在裂隙长度为500 m处的裂隙流体温度场特征.结果显示,在运行10年之后,文献8模型计算的流体温度为196 ℃,本模型计算的流体温度为200 ℃;在运行20年之后,文献8模型计算的流体温度为192 ℃,本模型计算的流体温度为197 ℃,两种模型计算得到的流体温度相差大约是4 ℃.由于采用热传导量来表征岩体对流体的加热比采用对流换热量来表征岩体对流体的加热更为精确,所以本研究中所采用的模型应属更优.
此外,本文模型中岩体的热传导方向只垂直于裂隙面,但实际上,热量传导是沿着最大温度梯度方向.单裂隙系统热开采过程中,由于受低温水的控制,水流入口处一直处于明显低温区,周缘高温区的热量都有向此区域汇集的趋势,使低温区得到一定热量补给,低温区展布形态必然与本文模拟的“三角形”展布有所不同,等温线会略凸向水流入口低温区.虽然二者的热量传输路径和温度场分布稍有差异,但热量最终均被输送到裂隙界面和水中,因此,本文模型的热传导计算对分析裂隙储层热开采效率和潜力的影响不大.
4.2 采热效率
采热效率是评价EGS储层性能的一个关键指标.采热效率受到岩体初始温度、裂隙特征和循环流体等诸多因素的影响,可简单表示为水岩即时温差比岩体初始温度与进水温度之差(Chen, et al., 2013).而对采热效率的影响主要体现在影响出口流体温度的因素上.结合数学模型理论分析和上述计算结果可以看出,在某特定热开采条件下,水沿裂隙流动,温度不断增加,当流经路径超过某一长度后,系统运行周期内的流体产出温度不再增长,体现了一定范围内的裂隙长度增加对采热效率表现为正效应.此外,裂隙宽度和水流速率对水岩温度场有近乎一致的影响,在裂隙宽度或水流速率增加后,相等幅度的流体温度上升需要更长的时间和流径,产水温度下降提前,采热效率降低,表现为负影响.
5 结 论
本文构建了针对EGS单裂隙热流耦合的数学模型,模型主要控制热流耦合时水岩温度场的演化,并以此计算了裂隙宽度和水流速率对水岩温度场的影响,分析了热在裂隙岩体中传递的过程及裂隙对采热效率的影响.研究发现:
1 )与前人模型结果对比,本模型在参数意义明确和易用性上表现出一定的优越性;
2)裂隙宽度和水流速率对水岩温度场的影响具有相近的影响效果;
3 )特定开采条件有确定的岩体温度影响半径;
4)进水口为明显低温区,并显示以水流前进的裂隙为对称面,向两侧岩体展开的近三角形采热区域;
5 )裂隙长度对采热效率表现为正效应,而裂隙宽度和水流速率对采热效率表现为负效应.
此外,文中首次推导给出了EGS热流耦合水岩温度场演化特征简明数学表达式;另一亮点是本文基于岩体热传导系数来考虑耦合过程中的热传导量.本文研究结果为今后更精细深入的EGS热流耦合、甚至多场耦合研究奠定了一定的理论基础,同时也对EGS的工程实施具有参考指导作用.
| [1] | Abé H, Niitsuma H, Murphy H. 1999. Summary of discussions, structured academic review of HDR/HWR reservoirs. Geothermics, 28(4-5):671-679. |
| [2] | Brown D W,Duchane D V. 1999. Scientific progress on the Fenton Hill HDR project since 1983. Geothermics,28(4-5):591-601. |
| [3] | Cheng A H D, Ghassemi A, Detournay E. 2001. Integral equation solution of heat extraction from a fracture in hot dry rock. International Journal for Numerical and Analytical Methods in Geomechanics,25:1327-1338. |
| [4] | Chen X Z, Li B G, D Y, et al. 2007. Analysis of water-rock heat transfer in fractured rock mass. NORTHWEST WATER POWER. (in Chinese),3:18-20. |
| [5] | Chen J L, Luo L, JIANG F M. 2013. Analyzing heat extraction and sustainability of enhanced geothermal systems (EGS) with a novel single-porosity model. In: Proceedings: Thirty-Eighth Workshop on Geothermal Reservoir Engineering. Stanford University, Stanford, SGP-TR-198. |
| [6] | Chen J L,LUO L,JIANG FM. 2013. Thermal compensation of rocks encircling heat reservoir in heat extraction of enhanced geothermal system. Chinese Journal of Computational Physics. (in Chinese),30(6):862-870. |
| [7] | Fox D B, Sutter D, Beckers K F, et al. 2013. Sustainable heat farming: Modeling extraction and recovery in discretely fractured geothermal reservoirs. Geothermics,46:42-54. |
| [8] | Gringarten A C, Witherspoon P A, Ohnishi Y. 1975. Theory of heat extraction from fractured hot dry rock. Journal of Geophysical Research, 80:1120-1124. |
| [9] | Gelet R, Loret B, Khalili N. 2012. A thermo-hydro-mechanical coupled model in local thermal non-equilibrium for fractured HDR reservoir with double porosity. Journal of Geophysical Research,117:B07205-B07228. |
| [10] | He L W, Jin Z H. 2010. A local thermal nonequilibrium poroelastic theory for fluid saturated porous media. Journal of Thermal Stresses,33:799-813. |
| [11] | Hu H P. 2010.The theory of heat conduction. Hefei: University of Science and Technology of China Press. (in Chinese). |
| [12] | Jiang F M, Luo L, Chen J L. 2013. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems. International Communications in Heat and Mass Transfer,41:57-62. |
| [13] | U.S. Massachusetts Institute of Technology. The Future of Geothermal Energy. (2007). http://geothermal.inel.gov. |
| [14] | McFarland R D, Murphy H D. 1976. Extracting energy from hydraulically fractured geothermal reservoirs. ASME,State Line,NV. |
| [15] | McLarty L.2000. Assessment of the State-of-the-Art of Numerical Simulation of Enhanced Geothermal Systems. Federal Geothermal Research Program Update Fiscal Year 1999. |
| [16] | Ogino F, Yamamura M, Fukuda T. 1999. Heat transfer from hot dry rock to water flowing through a circular fracture. Geothermics,28:21-44. |
| [17] | Sanyal K S, Butler S J, Swenson D, et al. 2000. Review of the state-of-the-art of numerical simulation of enhanced geothermal system. Proceedings World Geothermal Congress 2000. Kyushu-Tohoku:[s.n.]. |
| [18] | Sanyal S K, Granados E E, Butler S J, et al. 2005. An alternative and modular approach to enhanced geothermal systems.//World Geothermal Congress. California: Stanford Universiy, 139-144. |
| [19] | Shaik A R, Rahman S S, Tran N H, Tran T. 2011. Numerical simulation of fluid-rock coupling heat transfer in naturally fractured geothermal system. Applied Thermal Engineering,31:1600-1606. |
| [20] | SU Z,WU N Y,ZENG Y C,et al. 2012. Research and development of enhanced geothermal system: a case study of Fenton hill in New Mexico (USA). Progress in Geophys. (in Chinese), 27(2):0771-0779. |
| [21] | Tian L L. 2003. Experimental and numerical study on the Thermo-Hydrological coupling of fractured rocks [Master D. thesis].Beijing: Beijing Jiao Tong University. (in Chinese). |
| [22] | Wang X X, Wu N Y, Su Z, et al. 2012. Research progress of the Enhanced Geothermal Systems development technology. PROCESS IN GEOPHYSICS.(in Chinese),27(1):0355-0326. |
| [23] | Wang X X, Wu N Y, Zhang K N, et al. 2012. Multi- field coupling for enhanced geothermal system development. HYDROGEOLOGY & ENGINEERING GEOLOGY. (in Chinese), 39(2):126-130. |
| [24] | Wunder R, Murphy H. 1978. Thermal drawdown and recovery of singly and multiply fractured hot dry rock reservoirs. Informal Report W-7405-ENG.36. Los Alamos Scientific Laboratory of the University of California. |
| [25] | Yan Z J. 2004. Method of mathematical physic. Hefei: University of Science and Technology of China Press. (in Chinese). |
| [26] | Zhao Y S, Wan Z J, Kang J R. 2004. Introduction to HDR Geothermal Development. Beijing: Science Press. (in Chinese). |
| [27] | 陈兴周,李宝国,董源,等.2007.裂隙岩体水-岩传热分析. 西北水电,3:18-20. |
| [28] | 陈继良,罗良,蒋方明. 2013.热储周围岩石热补偿对增强型地热系统采热过程的影响. 计算物理, 30(6):862-870. |
| [29] | 胡汉平. 2010.热传导理论. 合肥:中国科学技术出版社. |
| [30] | 苏正,吴能友,曾玉超,等. 2012. 增强型地热系统研究开发:以美国新墨西哥州芬凳山为例. 地球物理学进展,27(2):0771-0779. |
| [31] | 田鲁鲁.2003.裂隙岩体渗流-传热耦合模型试验及数值模拟研究[硕士论文]. 北京:北京交通大学. |
| [32] | 王晓星,吴能友,苏正,等. 2012.增强型地热系统开发技术研究进展. 地球物理学进展,27(1):0355-0326. |
| [33] | 王晓星,吴能友,张可霓,等. 2012. 增强型地热系统开发过程中的多场耦合问题. 水文地质工程地质,39(2):126-130. |
| [34] | 严镇军. 2004. 数学物理方法.合肥:中国科学技术大学出版社. |
| [35] | 赵阳升,万志军,康建荣. 2004. 高温岩体地热开发导论.北京:科学出版社,2004. |
 2014, Vol. 29
2014, Vol. 29


