2. 中国科学院大学, 北京 100049;
3. 东华理工大学, 南昌 330013
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. East China Institute of Technology, Nanchang 330013, China
在地下流体动力学中,裂隙岩体的渗流是指流体在岩体多孔介质或裂隙介质(裂隙、断层等)中流动,其相关理论在油、气、水资源开发、环境保护和温室气体埋存等工程方面都有着重要的应用.由于裂隙储层的非均质性,因而其渗透性不可能直接观察;受实验条件的限制,大尺度、长时间、可以考虑多种因素影响的实验往往也无法实现.因而,数值模拟技术正成为研究储层渗透性的重要手段(刘振峰等,2003;王克文等,2006; 周波等,2007;刘得军等,2013;赵迎月等,2013).
Boardbent和Hammersley(Broadbent and Hammersly, 1957)在1956年提出了逾渗理论(Percolation Theory),最初逾渗模型被用于描述流体在随机多孔无序介质中的随机扩展和流动.岩体内部的多孔介质由许多狭窄且长的孔喉连接而成的相互连通的集团.随着外部条件而逐步演化成为贯通整个多孔介质的连通团.这种经典的逾渗理论研究仅仅局限于孔隙介质,忽略了裂隙这一主要的渗流通道.因此,孔隙介质的逾渗理论不能与地质体的渗流现象很好地符合.本文将裂隙引入到介质的逾渗研究中,建立了裂隙介质的逾渗研究方法,研究了流体在裂隙网络中的流动.
目前用来描述裂隙介质渗流的数学模型主要有两种(葛家理,2003;程汉鼎等,2007;周志芳,2007): 一是考虑岩体中裂隙系统和基质岩块系统的流体交换过程,即所谓的裂隙-孔隙双重介质模型; 二是忽略了两类系统间的流体交换过程,即非双重介质模型,包括等效连续介质模型和离散裂隙网络模型(Berkowitz,2002).对于低渗透储层,孔体的渗透率几乎为0,可以忽略.本文使用离散的裂隙网络模型研究流体在裂隙岩体中的渗流模型.裂隙网络渗流模型最初是由Wittke提出的,考虑了裂隙的形状、大小、密度和方向等参数.这类模型适合于低渗透储层,即渗透主要由裂隙控制的储层.应用该模型,需要进行野外调查,统计节理的分布规律,按照节理参数的分布概率,使用Monte Carlo理论随机生成小尺度裂隙网络模型.
近年来,国内外使用逾渗理论对裂隙储层的研究正在逐渐的深入,并对裂隙岩体的性状和渗流系统进行了较为深入的研究(朱大勇等,2007;冯增朝等,2007;Sadeghnejad et al., 2011;郑委等,2011;Jafari and Babadagli, 2013).朱大勇等(2007)用二维座逾渗模型描述裂隙岩体的渗透问题,得到了裂隙岩体渗透率的递推矩阵.冯增朝等(2007)等使用逾渗方法研究了孔隙裂隙双重介质的逾渗规律,给出了孔隙率、裂隙分形维数、裂隙数量分布初值与逾渗概率的关系.郑委等(2011)使用逾渗研究了裂隙多孔介质的连通性,并提出能够反映和比较裂隙多孔介质连通性的2个量化参数.周波(2006)利用狭窄平行板裂隙模型来模拟和分析单个裂隙内油气运移的过程,得到流体在裂隙中的运移路劲具有分形的特点.国内学者使用逾渗研究裂隙是小尺度,甚至是微观尺度的,而研究深层复杂岩体的渗透性都是基于大尺度甚至是盆地尺度的.Masihi和King(2007)假设低渗透储层中,裂隙控制着流体的流动,使用逾渗理论研究了估计裂隙储层连通性的方法.假定裂隙的方向是垂直的,使用FRACA软件建立裂隙的网络图,根据逾渗模型的尺度定律,得到裂隙的渗透性和无量纲化密度之间的乘幂关系(Jafari and Babadagli, 2013).但是逾渗模型的尺度定律的适用条件是模拟区域的边长是无限长的,因而在有限尺度的系统情况下,尺度定律是不合适的.另外,在成岩作用下,裂隙的方向分布是随机的.S.Sadeghnejad(2011)使用有限尺度转换定律,研究了储层中孔隙被占据概率和渗透性之间的关系,然后使用尺度放大思想(upscaling method),分别得到了储层的平均渗透性、平均连通性与占据概率之间的关系,并和实际数据对比.这些工作为本文中研究裂隙储层的渗透性模型的设计和实现奠定了基础.
本文使用裂隙网络模型,并结合连续逾渗理论和COMSOL Multiphysis中的自带的有限元方法求解器,研究低渗透储层的平均渗透性和无量纲化裂隙密度之间的关系.首先考虑了裂隙的分布方向、长度、密度和裂隙的开度,进而建立裂隙的网络图,而后通过引入排除体积,对裂隙的密度进行无量纲化,从而使得裂隙的渗透率和裂隙的形状无关,再根据有限尺度转换定律(King,1990; Stauffer and Aharony, 1992)和尺度放大方法(up-scaling method),使用重复子区域的方法研究每个小区域的渗透性,分析了不同尺度下裂隙储层平均渗透性和裂隙无量纲化密度之间的关系函数.将模拟结果和FRACA软件得到的渗透率值进行对比,泊松相关系数为0.885,结果较吻合.该模拟结果可以为石油勘探工程在定性分析深层复杂介质渗透率时提供一个依据,为逾渗理论从小尺度放大到宏观物理模型即储层尺度的应用提供了一个理论依据.
1 二维裂隙网络模型 1.1 裂隙网络模拟的假设
裂隙网络模拟的基本假设有四条:
(1)裂隙的迹线是由裂隙中点(x0,y0)、裂隙长度l、裂隙的方向θ(定义为自x轴逆时针旋转至裂隙的角度)和裂隙的开度a4个参数来确定,迹线开度的中点坐标为

(2)裂隙的模拟区域内,裂隙的中点服从均匀分布,裂隙的长度服从对数正态分布,裂隙的方向服从正态分布,裂隙的开度服从正态分布.
(3)模拟区域内的裂隙是狭窄的平面,迹长表示裂隙的长度,宽度表示裂隙的开度,方向表示裂隙的产状.
(4)模拟区域内裂隙的密度定义为区域内裂隙的总数(Khamforoush et al., 2008),即

1.2 裂隙网络模拟的生成
近年来,随着计算机的发展,建立在概率论和统计学基础上的裂隙网络模型研究得到了迅速的发展.裂隙网络的模拟主要是应用Monte Carlo方法.连续逾渗理论是处理具有强无序和随机结构系统的重要理论方法之一,本质上是概率论的一个分支.因而本文用连续逾渗理论方法和Monte Carlo方法来研究裂隙储层平均渗透率和裂隙岩体无量纲化密度之间的关系.
根据目前对岩体裂隙几何分布的研究成果以及工程实践可知,岩体裂隙的几何参数一般服从某一种或几种的概率密度分布.根据裂隙生成的四个假设,使用Matlab得到裂隙的网络图,如图 1.从图中可知:在相同裂隙长度情况下,随着裂隙密度的增加,流体在裂隙中运移的通道也增加.
 | 图 1 不同裂隙密度时的裂隙网络图 Fig. 1 The fracture network of different fracture density |
得到不同裂隙密度下的裂隙网络图后,给定流体的控制方程以及边界条件等,便可以得到流体在裂隙网络图中的速度分布和压力分布.
假定流体是单相的Newton流体,流动是定场、等温的,裂隙介质中的渗流速度很小,可以忽略对流作用.由于流体力学分析理论知,裂隙中的流动为层流,这时流体在裂隙介质的流动应满足Navier-Stokes方程,即:



采用有限元方法利用COMSOL Multiphysics求解器解方程(5)(贺瑶瑶和刘建军,2011).COMSOL Multiphysics是以有限元法为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来实现真实物理现象的仿真,被当今世界科学家称为“第一款真正的任意多物理场直接耦合分析软件”,因而本文使用COMSOL Multiphysics软件求解不同裂隙密度下的裂隙岩体渗透率值,图 2是流体通过裂隙密度为0.075时的速度分布图和压力分布图,可知,流体是沿着相互连通的裂隙中流动的.
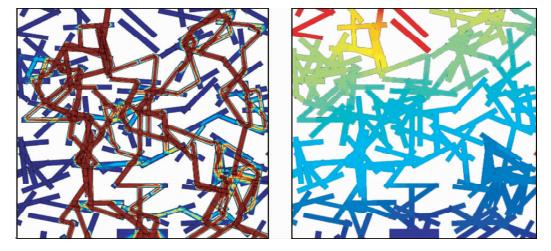 | 图 2 密度为0.075时裂隙的 速度和压力的分布 Fig. 2 The velocity distribution(a) and pressure distribution(b)of fracture at the density of 0.075 |
逾渗理论是概率论的一个分支,可以用来处理具有强无序和随机特征系统的重要理论方法之一,可以描述深层复杂几何结构系统的渗透性(Stauffer and Aharony, 1992).该理论的优点是许多具有强无序和随机结构系统的性质可以用简单的代数关系来表示,即尺度定律(scaling law)(King,1990)来表示.
逾渗模型包括二种基本模型:座逾渗(site percolation)和键逾渗(site percolation).假定座(或者键)被占据的概率为p,即流体可以通过的概率为p.对于很小的p,则存在很多孤立不连通的渗流团,流体不能通过;随着概率p的不断增加,渗流团中的单元数逐渐增加,当p达到某个临界值pc时,存在可以贯穿区域二边的渗流团,即流体可以从区域的一边流到另一边,该pc值称为逾渗阀值,与空间维数和网格的形状有关.在逾渗阀值pc处是存在尺度定律(Masihi M et al., 2007):

但是该乘幂关系只适用于无限大的储层,对于有限尺寸的储层并不适用.King(1990)提出了有限尺度转换定律(finite size scaling transformation)来研究有限尺寸的宏观裂隙储层的平均渗透性:
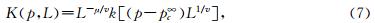
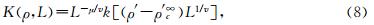
|
|
表 1 逾渗计算中的参数值 Table 1 Value of parameters used in percolation calculations |
Balberg等(1984)提出排除体积Aex的概念,将裂隙密度用排除体积来表示,无量纲化裂隙密度,从而使裂隙的有效渗透率和裂隙的形状无关(Vaentini et al., 2007).所谓排除体积Aex,就是在一个系统中,裂隙占据某一空间后,其余的裂隙仅能占据剩余的一定空间,体系总体积与允许其它裂隙占有的剩余体积之差就是被研究裂隙的排除体积.
二维裂隙网络模型中,排除体积Aex与裂隙长度l之间的关系为(Balberg et al., 1984)

裂隙的密度定义为单位面积区域内裂隙的数目,因而裂隙的密度表示为(Khamforoush et al., 2008)

对裂隙的密度进行无量纲化,表示(Balberg et al., 1984; Khamforoush et al., 2008)为

3 模拟计算结果与讨论
基于连续逾渗和Monte Carlo方法建立好的小尺度裂隙网络模型,然后用尺度放大思想进一步研究宏观裂隙储层的渗透性.以达西定律为基础的流体动力学模型中,尺度放大方法(upscaling method)的实现主要采用网格粗化的方法获得,即在更大的尺度上采用合适的方法获得某参数在低一 级网格的平均值(Kruel-Romeu and Noetinger, 1995;Jackson et al., 2003). 尺度放大方法又叫实空间重整化群方法(real space renormalization),其理论是Wilson于1974年提出的,是目前研究这些与尺度无关的过程的一种方法,已广泛应用于裂隙储层中的研究(Masihi et al., 2007;Sadeghnejad et al., 2011).图 3示意了Bryant关于粗视方法的概念.
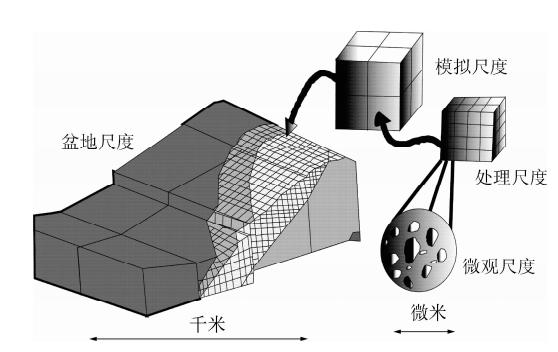 | 图 3 将孔隙尺度的模型扩展到 地质尺度过程示意图(Bryant,1988) Fig. 3 The diagram of pore scale model extended to the geological scale process |
为了研究裂隙储层的平均渗透率和无量纲化裂隙密度之间的关系,在不同尺度下(粗视化程度)对裂隙网络进行模拟.图 4是裂隙网络模型的尺度放大过程,用相对较少的网格来实现从微观尺度扩展到宏观的物理模型尺度及实际储层尺度的模拟.
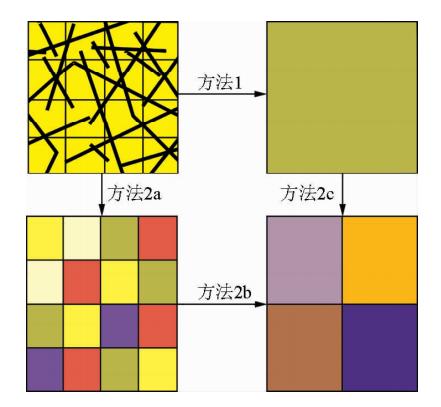 | 图 4 裂隙网络的尺度放大过程 Fig. 4 The upscaling process of fracture network |
在裂隙网络模型中,裂隙密度的大小直接决定了模型中裂隙数的多少.从定性分析来说,裂隙网络模型中随着裂隙条数的增加,流体在模型中流动的通道就越多,渗透率变大.本文通过给出一组变化的密度参数来定量分析尺度L=16时的裂隙储层渗透性,如表 2.
|
|
表 2 不同密度裂隙的逾渗性质 Table 2 The percolation properties of different density of fracture |
在模拟尺度(simulation scale)下,使用尺度放大思想中的第一种方法,分别研究了流体在研究区域为L=64,32,16,8,4这四个不同区域下的裂隙网络中运移,并用有限元方法得到流体裂隙网络中的渗透率.由于研究区域为L=64时,对该区域划分网格数非常多,计算量大,因而不易计算.本文采用重复子区域的方法(Multiply sub-region method),即尺度放大过程的第二个方法来研究流体在L=64研究区域下的裂隙网络中运移及渗透性,最后得到不同研究区域尺度下的平均渗透率.图 5分别是不同尺度下的裂隙储层渗透率、平均渗透率值和无量纲化密度之间的关系,即 KLμ/v与(ρ′-ρ∞c)L1/v之间的关系.模拟结果表明:对于有限尺度的宏观储层,其渗透率和裂隙储层无量纲化密度之间存在着正相关的关系,即随着裂隙密度的增加,裂隙储层的渗透性增加.
 | 图 5 无量纲化裂隙密度和渗透率在 不同尺度下的关系 Fig. 5 The relationship between the dimensionless fracture density and permeability at different scales |
FRACA是基于地质统计学的裂缝分析、描述与建模软件,而不是从应力及岩石机械性能出发研究储层裂缝发育机制的工具,所以不要求使用者具备复杂的力学和岩石破裂方面的知识,也不需要大量的相关岩石物理参数.因此,FRACA软件不仅是一个易学、易用、实用的裂缝分析、描述与建模工具,而且得到了成功的应用:塔里木油田桑南及桑塔木断垒奥陶系碳酸盐岩储层地质建模技术研究、塔里木油田塔河裂缝建模、哈萨克斯坦让纳若尔油田南油藏裂缝建模等.
为了验证该结果的可行性,设研究区域L=100 m,本文将模拟结果和FRACA软件得到的渗透率进行对比,如图 6.使用t检验得到模拟渗透率值和FRACA软件计算的渗透着值之间的泊松相关系数为0.885,相关度很好.
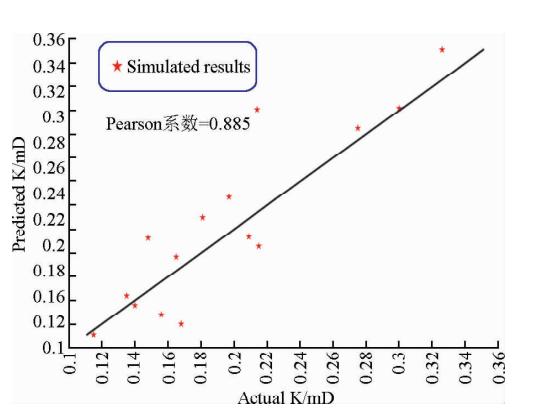 | 图 6 模拟裂隙渗透率和FRACA软件 得到的渗透率关系 Fig. 6 Predicted equivalent fracture network permeability vs. the actual permeability obtained using FRACA software |
该模拟结果可以为石油勘探工程在定性分析深层复杂介质渗透率时提供一个依据,为逾渗理论从小尺度放大到宏观物理模型即储层尺度提供了一个理论依据.
4 结果和讨论 4.1 使用Monte Carlo方法得到裂隙在不同密度下的网络图,基于COMSOL里的有限元求解器得到流体在裂隙网络图中的速度和压力分布,结果表明:随着裂隙密度的增加,裂隙的连通性增加,进而渗透性增加.
4.2 引入排除体积Aex,无量纲化裂隙密度,从而使裂隙的渗透性和裂隙的形状无关,进而可以简化深层复杂介质渗透性的计算. 4.3 使用有限尺度转换定律和尺度放大思想求得流体在裂隙储层中的平均渗透率和无量纲化裂隙密度之间的正相关曲线,该模拟结果和FRACA软件得到的渗透率值泊松相关系数为0.885,相关度很好,可以为石油勘探工程在定性分析深层复杂介质渗透率时提供一个依据,为逾渗理论从小尺度放大到宏观物理模型即储层尺度提供了一个理论依据. 4.4 低渗透储层具有复杂的地质特点,如何借助连续逾渗模型和尺度放大思想,研究深层复杂介质的渗透性,获得渗透率等参数的理论分析和定量计算,增强逾渗理论在油气田开发中的应用能力,值得进一步深入探讨.致 谢 本文受到国家重大油气专项(2011X05008-004-44)和国家自然科学基金(41376061)的资助,中科院南海所副研究员杨小秋老师以及审稿人的指导,特此致谢!
| [1] | Balberg I, Anderson C H, Alexander S, et al. 1984. Excluded volume and its relation to the onset of percolation[J]. Phys. Rev., (B30): 3933. |
| [2] | Berkowitz B. 2002. Characterizing flow and transport in fractured geological media: a review[J]. Adv. Water. Resour., 25(8-12): 861-884. |
| [3] | Broadbent S R, Hammersly J M. 1957. Percolation processes[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 53(3): 629-641. |
| [4] | Cheng H D, Chai J R, Li Y M. 2007. Brief overview on solute transport in fractured rock masses[J]. Water Resources and Power (in Chinese), 25(3): 33-37. |
| [5] | Feng Z C, Zhao Y S, Lü Z X. 2007. Study on percolation law of 2D porous and fractured double-medium[J]. Acta Physica Sinica (in Chinese), 56(5): 2796-2801. |
| [6] | Ge J l. 2003. The Modern Mechanics of Fluids Flow in Oil Reservior (in Chinese)[M]. Beijing: Petroleum Industry Press. |
| [7] | He Y Y, Liu J J. 2011. Numerical experimental research of equivalent seepage characteristic for fractured porous media[J]. Advances in Porous Flow (in Chinese), 1(2): 17-20. |
| [8] | Jackson M D, Muggeridge A H, Yoshida S, et al. 2003. Upscaling permeability measurements within complex heterolithic tidal sandstones[J]. Math. Geol., 35(5): 499-520. |
| [9] | Jafari A, Babadagli T. 2013. Relationship between percolation-fractal properties and permeability of 2-D fracture networks[J]. International Journal of Rock Mechanics & Mining Science, 60: 353-362. |
| [10] | Khamforoush M, Shams K, Thovert J F, et al. 2008. Permeability and percolation of anisotropic three-dimensional fracture networks[J]. Phys. Rev. E Stat Nonlin Soft Matter Phys., 77(5 Pt 2): 056307. |
| [11] | Kruel-Romeu R, Noetinger B. 1995. Calculation of intermodal transmissibilities in finite difference models of flow in heterogeneous media[J]. Water Resour. Res., 31(4): 931-959. |
| [12] | Liu D J, Ma Z H, Zhang Y Y, et al. 2013. Numerical simulation of the logging-while-drilling for fracture-vuggy reservoirs using adaptive FEM[J]. Progress in Geophysics (in Chinese), 28(2): 928-936. |
| [13] | Liu Z F, Hao T Y, Yang C C. 2003. Sedimention models and stochastic reservoir modeling[J]. Progress in Geophysics (in Chinese), 18(3): 519-523. |
| [14] | Masihi M, King P, Nurafza P. 2007. Fast estimation of connectivity in fractured reservoirs using percolation theory[J]. Soc. Pet. Eng. J., 12(2): 167-178. |
| [15] | Mourzenko V V, Thovert J F, Adler P M. 2005. Percolation and permeability of three dimensional fracture networks with a power law size distribution[M].// Fractals in Engineering. London: Springer, 81-95. |
| [16] | Sadeghnejad S, Masihi M, Pishvaie M, et al. 2011. Utilization of percolation approach to evaluate reservoir connectivity and effective permeability: a case study on North Pars gas field[J]. Scientia Iranica, 18(6): 1391-1396. |
| [17] | Stauffer,D, Aharony A. 1992. Introduction to Percolation Theory, 2nd edn., Taylor and Francis, London, UK. King, P.R. 1990. "The connectivity and conductivity of overlapping sand bodies", In 2nd Int. Conf. of North Sea Oil and Gas Reservoir, pp. 353-358. |
| [18] | Vaentini L, Perugini D, Poli G. 2007. The " small-world " topology of rock fracture networks[J]. Physica A: Statistical Mechanics and Its Applications, 377(1): 323-328. |
| [19] | Wang K W, Sun J M, Geng S C, et al. 2006. Percolation network study of shale effects on rock electrical properties under different salinity[J]. Chinese J.Geophys. ( in Chinese), 49(6): 1867-1872. |
| [20] | Zhao Y Y, Gu H M, Wang Y, et al. 2013. Research on constructing clastic reservoir seismic geologic model under well condition[J]. Chinese J. Geophys. (in Chinese), 56(6): 2055-2064. |
| [21] | Zheng W, Lu X B, Liu Q J, et al. 2011. Study of connectivity of fractured porous media based on dual-percolation model[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 30(6): 1289-1296. |
| [22] | Zhou B, Luo X R, Didier L, et al. 2006. Experiments and characterization of oil migration in a single fracture[J]. Acta Geologica Sinica (in Chinese), 80(3): 454-458. |
| [23] | Zhou B, Jin Z J, Luo X R, et al, 2007. Changing patterns of hydrocarbon migration pathway in a up-scaling percolation model[J]. Oil & Gas Geology (in Chinese), 28(2): 175-180. |
| [24] | Zhou Z F. 2007. Principle of Dynamics of Fractured Media (in Chinese)[M]. Beijing: Higher Education Press. |
| [25] | Zhu D Y, Fan P X, Guo Z K, et al. 2007. Recurrence matrix of permeable probability in percolation model for fractured rock mass[J]. Chinese Journal of Rock Mechanics and Engineering (in Chinese), 26(2): 262-267. |
| [26] | 程汉鼎, 柴军瑞, 李亚盟. 2007. 裂隙岩体溶质运移简述[J]. 水电能源科学, 25(3): 33-37. |
| [27] | 冯增朝, 赵阳升, 吕兆兴. 2007. 二维孔隙裂隙双重介质逾渗规律研究[J]. 物理学报, 56(5): 2796-2801. |
| [28] | 葛家理. 2003. 现代油藏渗流力学原理-上册[M]. 北京: 石油工业出版社. |
| [29] | 贺瑶瑶, 刘建军. 2011. 裂隙-孔隙介质等效渗透率的数值试验研究[J]. 渗流力学进展, 1(2): 17-20. |
| [30] | 刘得军, 马中华, 张颖颖,等. 2013. 缝洞型储层随钻测井自适应有限元法的数值模拟[J]. 地球物理学进展, 28(2): 928-936. |
| [31] | 刘振峰, 郝天珧, 杨长春. 2003. 沉积模型和储层随机建模[J]. 地球物理学进展, 18(3): 519-523. |
| [32] | 王克文, 孙建孟, 耿生臣,等. 2006. 不同矿化度下泥质对岩石电性影响的逾渗网络研究[J]. 地球物理学报, 49(6): 1867-1872. |
| [33] | 赵迎月, 顾汉明, 汪勇,等. 2013. 无井条件下建立碎屑岩储层地震地质模型研究[J]. 地球物理学报, 56(6): 2055-2064. |
| [34] | 郑委, 鲁晓兵, 刘庆杰,等. 2011. 基于双重逾渗模型的裂隙多孔介质连通性研究[J]. 岩石力学与工程学报, 30(6): 1289-1296. |
| [35] | 周波, 罗晓容, Didier L,等. 2006. 单个裂隙中油运移实验及特征分析[J]. 地质学报, 80(3): 454-458. |
| [36] | 周波, 金之钧, 罗晓容,等. 2007. 尺度放大时逾渗模型中的油气运移路径变化规律探讨[J]. 石油与天然质, 28(2): 175-180. |
| [37] | 周志芳. 2007. 裂隙介质水动力学原理[M]. 北京: 高等教育出版社. |
| [38] | 朱大勇, 范鹏贤, 郭志昆,等. 2007. 裂隙岩体逾渗模型中渗透概率递推矩阵[J]. 岩石力学与工程学报, 26(2): 262-267. |
 2014, Vol. 29
2014, Vol. 29


