0 引 言
地震波场模拟在地震勘探领域有多方面的应用,例如优化地震数据采集参数,为各种偏移成像方法提供输入数据等.地震波场模拟主要有积分数值解、微分数值解以及射线追踪方法.微分数值解又包括有限差分、有限元和傅氏变换法.本文将采用应用较多的有限差分方法来模拟波场传播.
Alterman和Karal首次将有限差分方法用于地震波场模拟,研究了弹性波在层状介质中的传播、反射以及面波等问题,并获得了弹性波的水平分量和垂直分量的地震记录(Alterman and Karal, 1968).此后,有限差分方法应用于二维非均匀介质(Kelly et al., 1976).以上研究所用的波动方程都是二阶双曲型波动方程,以质点的位移为未知量,采用差分格式时需要近似位移对时间和空间坐标的二阶导数,精度低且计算量较大.
通过对二阶波动方程降阶处理,将弹性波动方程转化为一阶速度-应力方程,可以降低计算量,提高模拟精度(Aki and Richards, 2002).Vireux利用基于一阶速度-应力方程的有限差分方法,分别模拟了SH波和P-SV波在二维非均匀介质中的传播(Virieux,1984;Virieux,1986).针对复杂介质中弹性波场的模拟,Dai等利用一阶波动方程模拟了弹性波在非均匀各项同性孔隙介质中的传播(Dai et al., 1995).一阶应力-速度方程不仅降低了单位波长的网格点数,而且提高了计算效率.
以上学者在采用有限差分求解波动方程时,都是在直角坐标系中采用规则网格实现的,但规则网格会产生“阶梯状”边界,会在模拟中作为绕射点产生模拟噪声.不规则网格的出现解决了此问题,并能保持较高的算法速度.
有限差分方法固有的一个缺陷是计算量较大,对计算机内存要求也较高.因为模拟时需要遍历空间每个网格点和每一个时间步长,所以在模拟较大规模网格的波场时,需要很大的计算机时.尤其是模拟精度要求较高,采取更小的时间和空间步长时,这种现象更加严重.因此,如何提高地震波场模拟的效率是一个很重要的课题.
除了在算法上提高波场模拟的效率之外,另外一种可行的方法是采用高性能计算.GPU(Graphics Processing Unit,图形处理单元)利用自身多线程并行执行的优势被广泛应用于波场模拟及偏移成像中.GPU集群MPI技术(Michéa和Komatitsch,2010)和CUDA顶点编程、FBO技术(王占刚和苑春方,2011)已经用于地震波场模拟的加速.
除了在正演模拟方面,GPU技术在叠前偏移、逆时偏移及多次波压制方面方面也发挥了重要作用.例如,利用GPU加速地震叠前时间偏移(李博等,2009)和地震叠前逆时偏移(李博等,2010);将GPU加速用于山地地震资料的叠前时间偏移(刘国峰等,2009);利用GPU加速了地震叠前逆时偏移高阶有限差分算法(刘红伟等,2010);将GPU加速技术应用于表面多次波的预测(石颖和王维红,2012).以上GPU技术在地震资料处理和偏移方面的应用,都极大的提高了计算效率,缩短了处理周期.目前,有些学者正在进行全波形反演的GPU加速研究.根据GPU现有的发展趋势,我们可以预料到:随着计算机技术的发展,GPU将会在地震数据处理、计算等方面发挥越来越重要的作用.
本文首先介绍有限差分波场模拟的基本原理,然后提出了一种利用GPU加速的实现方法,通过比较CPU和GPU上的运行时间,验证了该方法在节省计算时间上的优势.
1 基本原理1.1 一阶应力-速度声波方程组交错网格计算实现1.1.1 标量声波方程的一阶应力-速度方程
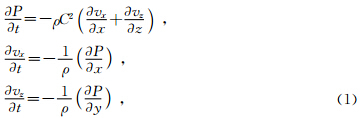
1.1.2 交错网格
规则网格是将地质模型划分为规则小矩形,所有物理量及其导数都在网格的节点上求取.而对于交错网格,对整数节点上的物理量求偏导是在半节点,对半节点的物理量求偏导是在整节点上.交错网格有限差分系数比规则网格有更好的收敛性,能够提高模拟精度和减少频散.
一阶应力-速度声波方程组中各个物性参数交错网格计算格式如下:在空间网格上,压力、体积模量参数在规则的网格节点上;而密度和x方向质点速度参数位于的x方向的半节点上,密度和z方向速度分量位于z方向的半节点上.其具体的分布情况可见图 1a.
在时间维度上,压力分布在整数的时间节点上,压力对时间的导数在半数节点求取;质点速度分量参数都位于半数时间节点上,对时间的导数是在整时间节点求取.其分布情况可见图 1b.
 | 图 1(a)二维交错网格物理量分布示意图;(b)时间维度上的网格点分布.(○为P、K参数位置、▲为νx,ρ参数位置,■为νz,ρ参数位置)Fig. 1(a)The distribution of parameters in the staggered grid;(b)Distribution of p and the Vx,Vz in the time dimension. |
一阶导数的任意2L阶精度有限差分近似格式(刘洋等,1998)可写为

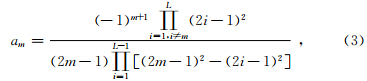
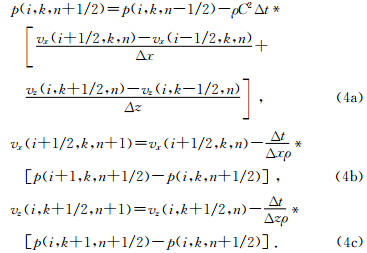
本文利用目前具有最好吸收效果的PML边界条件,来消除人工边界引起的反射波.PML方法在计算边界处引入一个吸收层,在这个层中,将所求的未知量的各个分量分解为两个辅助分量,一个平行于边界面,在方程中只保留平行于交界面方向的偏导数分量;一个垂直于边界面,只保留垂直于交界面方向的偏导数分量.最后对垂直于边界的分量引入阻尼因子,使界面上不产生反射的特征.Liu和Tao(1997)详细讨论了PML边界吸收条件在声波方程中的应用.
利用有限差分进行波场模拟时,需要考虑到差分方程的稳定性,一阶应力-速度方程组的交错网格高阶有限差分数值解法的稳定性条件为
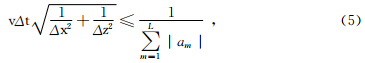
1.2 CUDA编程模型
CUDA编程模型将CPU作为主机(Host),GPU作为协作处理器(co-processor)或者设备(Device).在这个模型中,CPU与GPU协同工作,各司其职.CPU负责逻辑性较强的事物和串行计算,GPU则专注于执行高度线程化的并行处理任务.CPU、GPU各自拥有相互独立的存储器,可以实现主机与设备间的数据传输.
我们把并行计算的工作交给GPU.运行在GPU上的CUDA函数称为Kernel(内核函数).一个Kernel中存在两个层次的并行,一个是Grid中的Block间的并行和Block中的Thread间的并行(见图 2).我们将利用这两层并行执行模型,把每个网格点波场计算的任务分配给独立的线程,由所有的线程并行执行,加快计算效率.
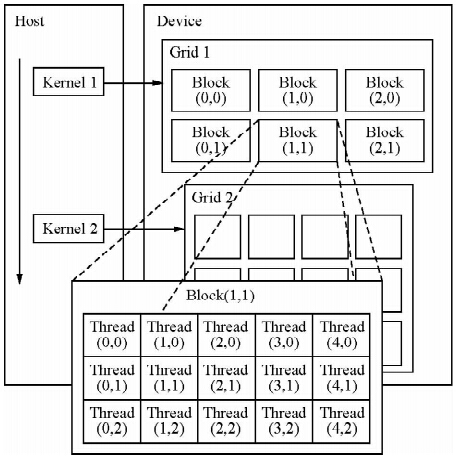 | 图 2 CUDA编程模型Fig. 2 The CUDA programming model |
2 GPU上实现数值模拟
目前,通用的GPU编程平台被称为CUDA.算法设计的主要问题就是如何把各个节点的计算量均匀地加载到各线程.为此,我们将速度网格的坐标映射到线程块中,以取代CPU算法中关于横坐标、纵坐标的循环.
需要在GPU上执行的操作有:
1 )x、z方向上整数节点处质点运动速度的微分;
2)整数节点处t+1时刻的声波压力值(加震源项);
3 )x、z方向半数节点处声波压力的微分;
4)t+1时刻半数节点的x、z方向的质点速度值.以计算整数节点的声波压力为例,详细介绍GPU的计算原理.
首先将加了PML吸收层地质模型分为如图 3a所示的子块(图中已用蓝、白两色分开),每个子块的规模相同.每个整数节点上t时刻的压力值已知.相应的,在GPU端分配和地质模型子块数目同样多的线程块(Thread Block),如图 3b所示.每个线程块负责对应的地质子块的声波压力差分值的计算.
 | 图 3(a)地质模型网格(斜线部分为PML吸收层);(b)Kernel函数分配的与地质模型对应的线程块,每个线程块负责对应子块数值的计算;(c)二维线程块分配的共享内存(中间白色部分为BLOCKD_DIMY X BLOCK_DIMX,对于空间2N阶精度的有限差分,四周蓝色部分为N×BLOCK_DIMX(Y))Fig. 3(a)The grid of geological model(the PML layer is marked by slash);(b)Thread block allocated to Kernel,each block is responsible for corresponding subblock;(c)Example of 2D block assigned to the shared memory.The block size is BLOCKD_DIMY *BLOCK_DIMX(white).For 2N order finite-difference,N ghost points are also required to be assigned(blue) |
若有限差分的空间精度为2N阶,计算x(z)方向上(i+1/2,j)节点处声波压力的微分则需要从全局内存读取该节点左侧(上侧)和右侧(下侧)各N个节点的压力值.读取的(i±n,j)(n=0,1,2,…,N-1)数据将与该点关于(i+1/2,j)对称节点的压力值做一次减法,两者之差再与差分系数做一次乘法.也就是说,每做两次运算,就需要从访问速度较慢的全局内存中访问两次.全局内存带宽严重限制了GPU超强的浮点运算能力.为此,借助于速度较快但是容量较小的共享内存减少对全局存储器的访问次数.假设每个二维线程块的规模为BLOCK_DIMX x BLOCK_DIMY,为每个线程块分配大小为(BLOCK_DIMX+N)x(BLOCK_DIMY+N)大小的共享存储器(如图 3c).这样分配的原因是对于子块临近边界附近N以内的节点,计算微分时需要用到相邻子块内节点的压力值.线程块内的各个线程负责从全局内存读取各自对应节点的压力值.当压力值存储在共享存储器之后,每个值可以多次用于微分值的计算.以8×8的线程块和N=4为例,共享内存中数据被用到的次数如图 4所示.可见,从全局内存读取一个压力值存放到共享存储器之后,可以被该线程块内计算其他节点的线程使用8~14次,提高了浮点运算与数据访问次数的比值,有利于计算的加速.
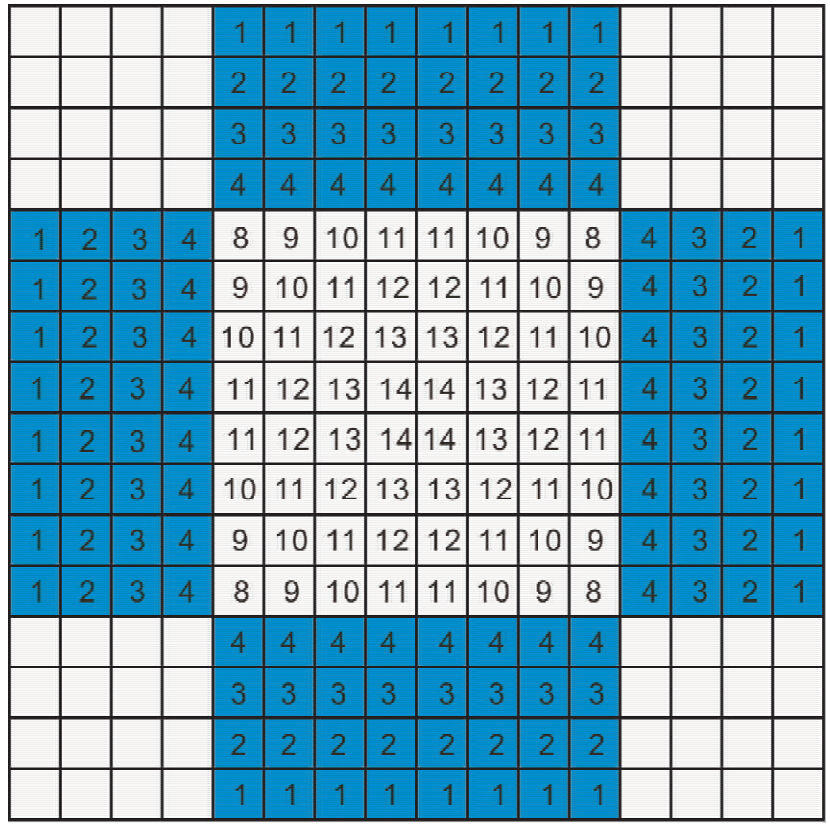 | 图 4 块共享内存中数据使用次数Fig. 4 The number of use of one data in shared memory |
对于频繁读取且不会变更的差分系数,将其存储在访问速度较快的常数存储器.按照各个线程在Grid中的索引,各线程所计算出的结果都存储到较大容量的全局存储器,以供t+1时刻计算质点速度使用.
类似的,质点速度的x、z方向的偏微分计算采用同样的策略. 3 测试分析
通过CUDA编程平台实现本文方法.测试环境为CPU:Intel Core i7-2600,3.40 GHz,16 G 内存.显卡配置为:NVidia GeForce GTX580,512个核心,3 G显存,GPU时钟频率为1.54 GHz.Warp size 为32,每个Block所能容纳的最大线程数为1024.选用Centos6.4操作系统.模拟的迭代次数设定为2500次,每隔10个时间步长存储一次波场快照.
模型为边角模型,如图 4所示:模型的空间步长都为5 m.依次采用128×128、256×256、512×512、1024×1024,2048×2048的网格规模.表 1显示了GPU、CPU的模拟时间、加速比,图 5显示了CPU与GPU的时间对比结果.
|
|
表 1 CPU端、GPU端不同网格规模的模拟时间对比 Table 1Comparison of CPU and GPU time |
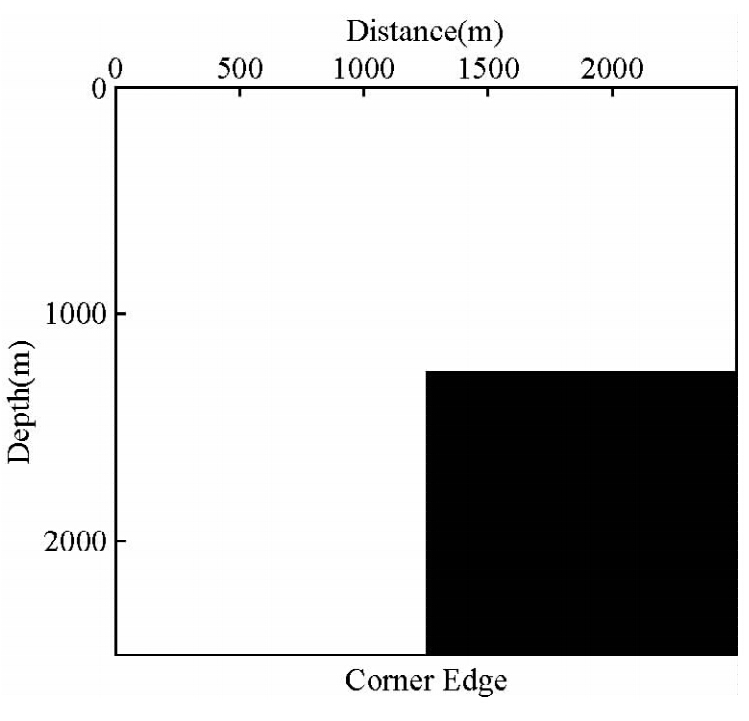 | 图 5 模拟所用的边角模型Fig. 5 Core-edge model |
从表 1和图 6可以看出:不论是在CPU端还是在GPU/CPU端,随着网格规模的不断增加,所需要的计算机时都近似呈指数增加.可以预见,当网格规模很大时,模拟的高效率将是生产中的一个重要考虑因素.但是,图 6明显的表明了GPU所需机时的增长速度要远远小于CPU的增长速度.因此,GPU将更加适用于大规模网格的模拟.另外,GPU相对CPU所用时间的加速比是不断增加的,该结果表明,网格规模越大,GPU加速技术所带来的高效率越显著.
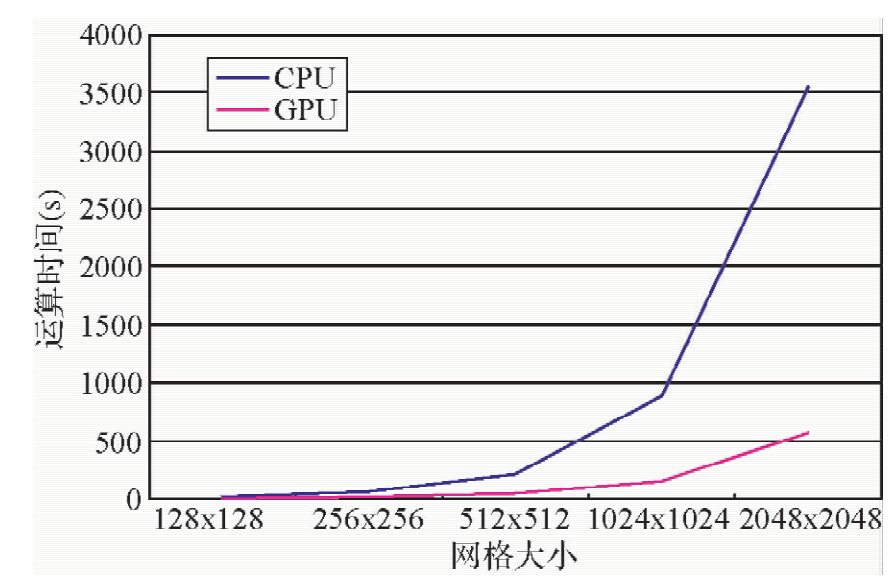 | 图 6 CPU端、GPU端不同网格规模的模拟时间(単炮)对比Fig. 6 Comparison of CPU and GPU time with different grid points |
4.1 通过CPU和GPU对比可以看出:GPU加速的算法可以缩短模拟时间,其关键原因是分块策略减少了程序对全局内存的访问,且各线程块并行计算取代了CPU端耗时的循环计算.尤其是当网格规模越大时,节约的时间越多.因此,GPU加速的波场模拟可以适用于大规模网格波场正演模拟,将在生产实际中得到广泛应用.
4.2 在CUDA编程时,计算效率主要由算法的并行度及其不同类型的内存使用策略有关.由于CUDA对每个块内的线程数限制在512个以下,块内的共享内存容量也较小,因此,若要开发计算效率更高的计算方案,还需要优化并行算法及内存存储策略.
致 谢 感谢审稿专家的帮助和支持.
| [1] | Aki K, Richards P G. 2002. Quantitative Seismology: Theory and Methods[M]. University Science Books. |
| [2] | Alterman Z, Karal F C Jr. 1968. Propagation of elastic waves in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 58(1): 367-398. |
| [3] | Dai N, Vafidis A, Kanasewich E R. 1995. Wave propagation in heterogeneous, porous media: a velocity-stress, finite-difference method[J]. Geophysics, 60(2): 327-340. |
| [4] | Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms: a finite-difference approach[J]. Geophysics, 41(1): 2-27. |
| [5] | Li B, Liu G F, Liu H. 2009. A method of using GPU to accelerate seismic pre-stack time migration[J]. Chinese J. Geophys. (in Chinese), 52(1): 245-252. |
| [6] | Li B, Liu H W, Liu G F, et al. 2010. Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J]. Chinese J. Geophys. (in Chinese), 53(12): 2938-2943. |
| [7] | Liu G F, Liu H, Li B, et al. 2009. Method of prestack time migration of seismic data of mountainous regions and its GPU implementation[J]. Chine J. Geophys. (in Chinese), 52(12): 3101-3108. |
| [8] | Liu H W, Li B, Liu H, et al. 2010. The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J]. Chinese. J. Geophys. (in Chinese), 53(7): 1725-1733. |
| [9] | Liu Q H, Tao J P. 1997. The perfectly matched layer for acoustic waves in absorptive media[J]. Journal Acoustical Society America, 102(4): 2072-2082. |
| [10] | Liu Y X, Li C C, Mou Y G. 1998. Finite-difference numerical modeling of any even-order accuracy[J]. OGP (in Chinese), 33(1): 1-10. |
| [11] | Michéa D, Komatitsch D. 2010. Accelerating a three-dimensional finite-difference wave propagation code using GPU graphics cards[J]. Geophysics Journal International, 182(1): 389-402. |
| [12] | Shi Y, Wang W H. 2012. Method for multiples attenuation of seismic data (in Chinese)[M]. Beijing: Geological Publishing House. |
| [13] | Virieux J. 1984. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 49(11): 1933-1942. |
| [14] | Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 51(4): 889-901. |
| [15] | Wang Z G, Yuan C F. 2011. Research on GPU accelerated 2D seismic wave modeling[J]. Computer Engineering (in Chinese), 37(9): 9-11. |
| [16] | 李博, 刘国峰, 刘洪. 2009. 地震叠前时间偏移的一种图形处理器提速实现方法[J]. 地球物理学报, 52(1): 245-252. |
| [17] | 李博, 刘红伟, 刘国峰,等. 2010. 地震叠前逆时偏移算法的 CPU/GPU 实施对策[J]. 地球物理学报, 53(12): 2938-2943. |
| [18] | 刘国峰, 刘洪, 李博,等. 2009. 山地地震资料叠前时间偏移方法及其GPU实现[J]. 地球物理学报, 52(12): 3101-3108. |
| [19] | 刘红伟, 李博, 刘洪,等. 2010. 地震叠前逆时偏移高阶有限差分算法及GPU实现[J]. 地球物理学报, 53(7): 1725-1733. |
| [20] | 刘洋, 李承楚, 牟永光. 1998. 任意偶数阶精度有限差分法数值模拟[M]. 石油地球物理勘探, 33(1): 1-10. |
| [21] | 石颖, 王维红. 2012. 地震资料表面多次波压制方法[M]. 北京: 地质出版社. |
| [22] | 王占刚, 苑春方. 2011. GPU 加速的二维地震波场模拟研究[J]. 计算机工程, 37(9): 9-11. |
 2014, Vol. 29
2014, Vol. 29


