地球物理学进展  2014, Vol. 29 Issue (3): 1201-1205   PDF    
引用本文
马德堂, 杨春雨, 李绪宣. 2014. 基于双线性插值的三维横向各向同性介质初至波射线追踪[J]. 地球物理学进展, 29(3): 1201-1205, doi: 10.6038/pg20140327  
MA De-tang, YANG Chun-yu, LI Xu-xuan. 2014. Preliminary waves ray tracing by linear travel-time interpolation method in 3-D transversely isotropic medium. Progress in Geophysics, 29(3): 1201-1205, doi: 10.6038/pg20140327   
基于双线性插值的三维横向各向同性介质初至波射线追踪
马德堂1, 杨春雨1, 李绪宣2    
1. 长安大学 地测学院, 陕西 710064;
2. 中海油研究总院, 北京 100027
收稿日期: 2013-9-9 修回日期: 2014-1-15 .
基金项目：国家科技重大专项课题（2011zx05024-001-03）资助.
作者简介：马德堂，1965年生，长安大学地测学院教师，副教授，陕西旬阳人，现从事地球物理教学及科研工作.（E-mail：madetang2004@163.com）
摘要：给出了基于旅行时双线性插值（LTI）的三维横向各向同性（VTI）介质中的地震初至波旅行时计算及射线追踪方法，通过三维均匀及水平层状VTI介质模型的试算，证实了该方法的准确性及适应性.该方法可用于三维VTI介质中的深度偏移及层析成像.
关键词： 射线追踪     地震波旅行时     线性插值     三维横向各项同性介质    
Preliminary waves ray tracing by linear travel-time interpolation method in 3-D transversely isotropic medium
MA De-tang1, YANG Chun-yu1, LI Xu-xuan2    
1. Changan University, Xian, Shanxi 710064, China;
2. CNOOC Research Institute, Beijing 100027, China
Abstract: In the paper, linear travel-time interpolation method based on Fermat's principle is applied to calculate seismic first-break time and seismic ray path tracing in 3-D transversely isotropic media is given. Based on three dimensional uniform and horizontal layer transversely isotropic medium model trial proved the feasibility of this method and accuracy, This method can be applied to the three dimensional transverse isotropic medium depth migration and seismic tomography research.
Key words: ray tracing     seismic travel-time     linear interpolation     3-D transversely isotropic medium    
0 引 言

射线追踪在地震资料的正反演中起着重要的作用，广泛应用于地震波的层析成像、偏移成像及震源精确定位等处理 环节之中(高尔根，1998；张钋，2000；张建中， 2003，2004；张永刚，2003).因此，地震波射线追踪方法的改进与应用倍受关注.

基于费马原理的旅行时线性插值射线追踪方法(LTI)最早由Asakawa等人(1993)提出，它具有适应性强、稳定、效率高、计算速度快等特点(Asakawa，1991；赵改善等， 1991，1998).马德堂等将LTI方法推广、应用到适应任意各向异性强度的二维横向各向同性(VTI)介质及TTI介质中的射线追踪(马德堂等， 2005，2011)；彭直兴和沈中民在LTI方法原理的基础上，给出了一种基于双线性插值的计算三维地震波旅行时的方法原理，并验证了该方法的正确性，同时也证明了该方法具有较高的精度(彭直兴，2005)；同时张东，傅相如等提出基于LTI和网格界面剖分三维射线追踪算法，该算法既可获得高精度最小全局走时和射线路径，又具有快速稳定等特点(张东等， 2009a，b)；梅胜全等又提出了基于改进的双线性旅行时插值的三维射线追踪方法，进一步提高双线性插值算法的精度和效率(梅胜全等，2010).在三维各向同性介质中，双线性插值射线追踪方法已有较快的发展，但还未见到三维各向异性介质中基于双线性插值的射线追踪方法.

本文在前人的基础上，将双线性插值方法推广到三维 VTI介质中的初至波旅行时计算及射线追踪，取得了较好的效果.

1 方法原理

1.1 三维VTI介质相速度和群速度计算

Berryman给出的利用5个独立弹性参数c11、c13、c33、c44、c66计算VTI介质中qP波、qSV波及qSH波的相速度的精确表达式(Berryman，1979；戚艳萍，2008；吴国忱等2005，2009)为

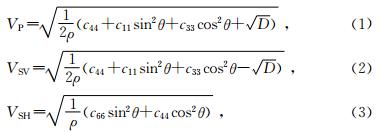
其中，D=[(c11－c44)sin2θ－(c33－c44)cos2θ]2+4(c13+c44)2sin2θcos2θ，θ为波前法线方向与Z轴正向的夹角，即相角.

群速度可用相速度表示，Berryman(1979)给出的表达式为

其中，V是相速度，k是波矢量的模，kH=ksinθ，kz=kcosθ.Crampin(Crampin，1981)按4式推导的VTI介质的分量形式的群速度表达式为

在VTI介质中，射线与Z轴夹角为群角，射线水平投影与X方向夹角为射线的方位角，这里分别用θ′表示.根据5式可得到计算θ′及群速度VG的公式为

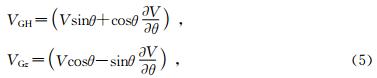
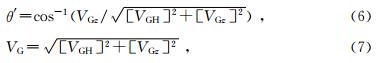
若将(1)式代入(5)式，然后再代入(6)式和(7)式，则群角θ′和群速度VG可分别表达为相角θ的显示函数，但表达式较复杂，而且在下面的双线性插值射线追踪中，首先设定的是群角θ′而不是相角θ.为此，在实现双线性插值射线追踪之前，先生成相角θ与群角θ′和群速度VG的离散关系表，即给定相角θ的一系列离散值，按(1)式、(5)式、(6)式、(7)式计算出对应的群角θ′和群速度VG的离散值.在实现双线性插值射线追踪时，对于给定的群角θ′，从上述表中查找或线性插值出其对应的群速度VG，便可计算射线走时. 如图 1为当弹性参数分别取c11=6.3×109 N/m2、c13=2.25×109 N/m2、c33=4.51×109 N/m2、c55=1×109 N/m2、c66=1.5×109 N/m2时，根据所生成的离散关系表绘出的θ与θ′、θ与VG及θ′与VG的关系曲线.

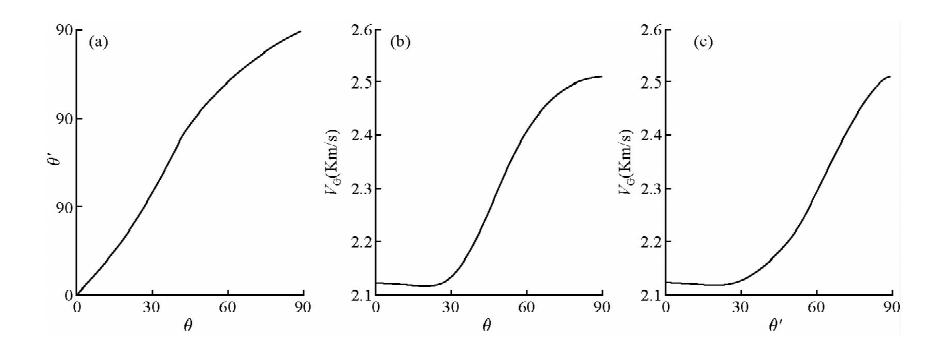图 1 相角、群角及群速度关系曲线图 (a)相角与群角；(b)相角与群速度；(c)群角与群速度. Fig. 1 Relation of phase angle、group angel and group velocity (a)Phase angle and group angel;(b)Phase angle and group angel;(c)Group angle and group velocity.
1.2 三维VTI介质初至波射线追踪的双线性插值算法

基于双线性插值的射线追踪可分为“向前”和“向后”两部分.“向前”过程：首先将弹性参数模型网格化，然后从震源开始计算其所在单元节点的最小旅行时，然后再以该单元为激发单元，以该单元各节点的最小旅行时为基础，依次求取其它单元上各节点的最小旅行时，直至求出所有网格节点上的最小旅行时；“向后”过程：从接收点所在单元开始，计算出该单元边界上所有主节点及次级节点到接收点的旅行时，将旅行时最小的节点作为所追踪射线上的一个节点，然后以该节点为新“接收点”，按照同样的方法寻找射线路径上的下一个节点，直至追踪到震源位置，从而得到射线路径.

基于双线性插值的三维VTI介质中的初至波射线追踪算法的核心有两点: 旅行时双线性插值和最小旅行时搜索.

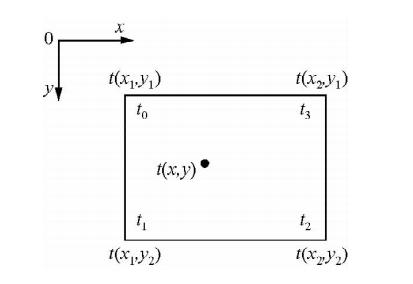图 2 矩形单元内旅行时插值示意图 Fig. 2 Schematic diagram of getting seismic Travel-time in the giant grid
1.2.1 旅行时双线性插值

如图 2所示，设XOY平面内四边形ABCD的顶点处的旅行时ti(i=0，1，2，3)已知，其内部任意点(x，y)处的旅行时用如下的双线性插值函数表示.

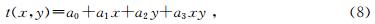
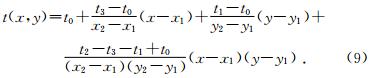
其中ai(i=0，1，2，3)为插值系数，可根据四边形的顶点坐标和顶点处的旅行时ti(i=0，1，2，3)求出，(8)式化为

同理，平行于XOZ平面的矩形单元内任意点的旅行时插值方程为

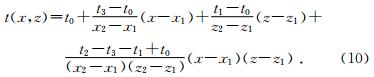
平行于YOZ平面的矩形单元内任意点的旅行时插值方程为

1.2.2 最小旅行时搜索

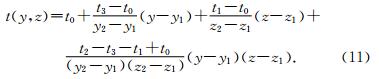
如图 3所示，设某条射线穿过矩形单元ABCD到达单元外给定点F，在四个顶点的旅行时tA、tB、tC及tD已知时，求射线穿过矩形单元的点E及F点处的最小旅行时.

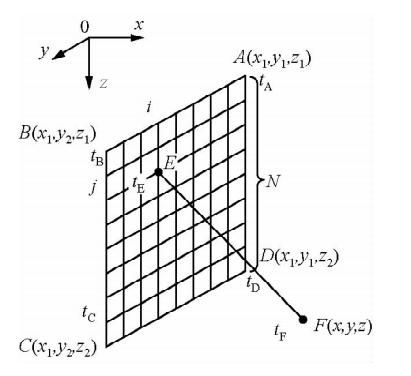图 3 网格面内次级节点示意图 Fig. 3 Schematic diagram of the secondary node

将矩形单元ABCD再离散化为多个小单元，每个小单元的顶点Eij称为次级节点，其坐标记为(x1，yi，zj)，其中：

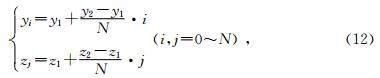
根据(10)式可得任意次级节点的旅行时为

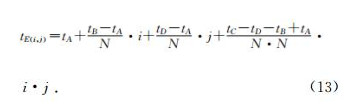
任意次级节点到达F点的旅行时为

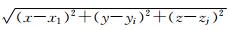其中，dEF= 为任意次级节点Eij到F点的距离，为群速度.

群速度VG是先按下面的(15)式计算出相应的群角，再从群角和群速度的离散关系表中查找或线性插值得到的.

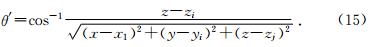
按(13)式和(14)式计算出所有次级节点到F点旅行时tF(i，j)，其中最小的就作为F点处的最小旅行时，对应的次级节点作为射线穿过矩形单元的点E.

2 模型算例 2．1 均匀VTI介质模型算例

该算例为均匀横向各向同性介质，模型弹性参数见表 1，弹性参数单位为109 N/m2.模型长、宽、高均为800 m，震源坐标为(400 m，400 m，400 m)，图 4左、中、右分别为过震源点的平行XOY面、XOZ面及YOZ面的平面内的初至波旅行时等值线图.

图 4 算例1的初至波旅行时等值线图 Fig. 4 Contour map of preliminary wave travel-time of example 1

表 1 模型1弹性参数 Table 1 Elastic parameters of model 1
2.2 水平层状VTI介质模型算例

模型的分层及各层的弹性参数见表 2，深度单位是米，弹性参数单位为109 N/m2.震源坐标为(500 m，200 m，1000 m)，检波器垂直排列，其X、Y坐标为(200 m，150 m).图 5左、中、右分别为过震源点的平行XOY面、YOZ面及XOZ面的平面内的初至波旅行时等值线图.图 5为从震源到检波器的初至波射线路径图.

表 2 模型2弹性参数 Table 2 Elastic parameters of model 2

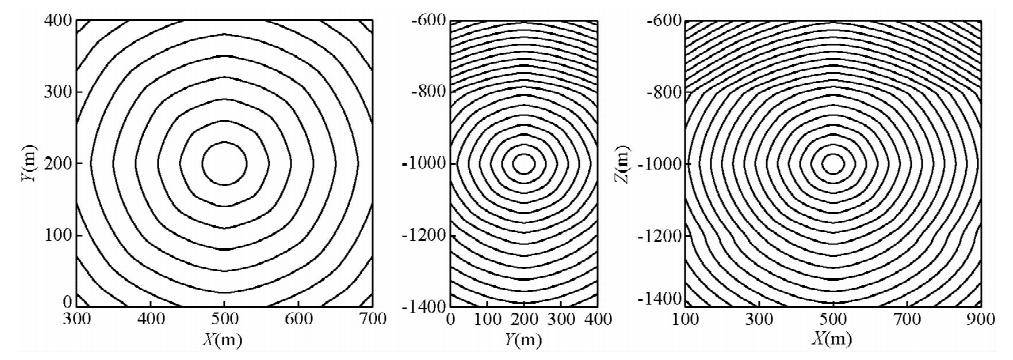图 5 算例2的初至波旅行时等值线图 Fig. 5 Contour map of preliminary wave travel-time of example 2
3 结 论

通过模型试算，证实了文中给出的基于双线性插值的射线追踪方法在三维横向各向同性介质中能够快速且较准确地计算出初至波旅行时，正确地追踪初至波射线路径，适用层状介质等较复杂的三维地质模型.该方法可应用于井间地震各向异性层析成像及偏移成像处理.

致 谢 本文查阅引用了相关文献，在此表示感谢！同时感谢审稿专家和编辑部老师的指导和帮助. 

参考文献
[1] Asakawa E, Kawanaka T. 1993. Seismic ray tracing using linear travel time interpolation[J]. Geophysics Prospecting, 41(1):99-112.
[2] Berryman J.G. 1979. Long-wave elastic anisotropy in transversely isotropic media[J]. Geophysics,44:896-917.
[3] Crampin S. 1981. A review of wave motion in anisotropic and cracked elastic-media[J], Wave Motion,3:343-391.
[4] Gao E G, Xu G M, Zhao Y. 1998. Ray tracing method[J]. Oil Geophysical Prospecting,33(1): 54-60.
[5] Ma D T. 2005. Numerical simulation of elastic wave field and cross-hole seismic first arrival wave travel time tomography[D]. Xi'an: Chang'An University.
[6] Ma D T, Zhu G M, Fan T E. 2011. 2D TTI medium primary wave travel search algorithm[J]. Oil Geophysical Prospecting,46(5):710-714.
[7] Mei S Q, Deng F, Zhong B S, Zhou X X. 2010.3D Seismic ray tracing algorithm based on the improved double linear travel interpolation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2(32):152-157.
[8] Peng Z X. 2005. Ray Tracing Forward Modeling with Seismic First Arrival Times[D].Chengdu: Chengdu University of Technology.
[9] Wu G C. 2005. Propagation and Migration for seismic wave in anisotropic media[M]. Dongying: Press of UPC,1-85.
[10] Wu G C, Liang K, Qi Y P. 2009. Phase velocity and group velocity in 3D TTI media[J]. Progress in Geophys, 24(6): 2097-2105.
[11] Qi Y P. 2005. The Study on qP Wave Forward Modeling Methods in 3D VTI Media[D]. Dongying: China University of Petroleum.
[12] Zhang D, Fu X R, Yang Y, et al. 2009a. 3-D Seismic ray tracing algorithm based on LTI and partition of grid interface[J]. Geophys.(in Chinese), 52(9):2370-2376.
[13] Zhang D, Xie B L, Yang Y, et al. 2009b. A ray tracing method based on improved linear travel-time interpolation[J].Geophys.(in Chinese), 52(1): 200-205.
[14] Zhao G S. 1991. Fast ray tracing algorithm[J]. Oil Geophysical Prospecting.,26(2):145-151.
[15] Zhao G S, Hao S L, Yang E H. et al. 1998. Seismic ray tracing algorithm based on the liner travel-time interpolation[J]. Geophysical prospecting for Petroleum,37(2):14-25.
[16] Zhang J Z, Chen S J,Xue C W. 2004. A method of shortest path ray tracing with dynamic network[J].Geophys(in Chinese),47(5):899-904.
[17] Zhang P, Liu H, Li Y M. 2000.The situation and progress of ray tracing method research[J]. Progress in Geophysics, 15(1):36-45.
[18] Zhang Y G. 2003. Seismic wave field numerical simulation method[J]. Geophysical Prospecting for Petroleum, 42(2):143-148.
[19] Zhang Z Z, Chen S J. 2003. Complex media seismic first-arrival wave numerical simulation[J]. Chinese Journal of Computational Physics,20(5):429-433.
[20] Zhou B, Greenhalgh S. 2006. Ray-path and travel-time computations for 2D transversely isotropic media with dipping symmetry axes[J]. Exploration Geophysics, 37: 150-159.
[21] Zhou B. 2004 On the computation of elastic wave group velocities for a general anisotropic medium[J]. Geophysics Eng,1: 205-215.
[22] 高尔根,徐果明,赵燚. 1998. 射线追踪方法[J].石油地球物理勘探,33(1):54-60.
[23] 马德堂. 2005.   弹性波场数值模拟及井间地震初至波旅行时层析成像[D][博士论文],西安:长安大学.
[24] 马德堂,朱光明,范廷恩.2011.二维TTI介质中初至波旅行时的搜索算法[J].  石油地球物理勘探,46(5):710-714.
[25] 梅胜全,邓飞,钟本善,等. 2010.基于改进的双线性旅行时差值的三维射线追踪[J].  物化探计算技术,2(32):152-157.
[26] 彭直兴. 2005. 地震波初至旅行时射线追踪正演方法研究[D][硕士论文].   成都:成都理工大学.
[27] 戚艳萍. 2008. 三维VTI介质qP波正演方法研究[D].   东营:中国石油大学.
[28] 吴国忱. 2005. 各向异性介质地震波传播与成像[M],东营:中国石油大学出版社,1-85.
[29] 吴国忱,梁楷,戚艳萍. 2009. 三维TTI介质相速度和群速度[J]. 地球物理学进展, 24(6):2097-2105.
[30] 张东,傅相如,杨艳,等. 2009a.基于LTI和网格界面剖分的三维地震射线追踪算法[J].  地球物理学报,52(9):2370-2376.
[31] 张东,谢宝莲,杨艳,等. 2009b.一种改进的线性走时插值射线追踪算法[J].  地球物理学报,52(01):200-205.
[32] 张建中,陈世军. 2003. 复杂介质地震初至波数值模拟[J].   计算物理, 20(5):429-433.
[33] 张建中,陈世军,徐初伟.2004.动态网络最短路径射线追踪[J].   地球物理学报,47(5):899-904.
[34] 张钋,刘洪,李幼铭. 2000.射线追踪方法发展现状[J].地球物理学进展,15(1): 36-45.
[35] 张永刚. 2003. 地震波场数值模拟方法[J]. 石油物探, 42(2):143-148.
[36] 赵改善.1991. 快速射线追踪算法[J].  石油地球物理勘探, 26(2):145-151.
[37] 赵改善,郝守玲,杨尔皓,等. 1998. 基于旅行时线性插值的地震射线追踪算法[J].  石油物探,37(2):14-25.