2. 同济大学海洋与地球科学学院波现象与反演成像研究组, 上海 200092
2. Tongji University, School of Ocean and Earth Science Wave Phenomenon and Inversion Imaging Team, Shanghai 200092, China
复杂地表复杂构造是近年来陆上地震勘探的重难点问题.随着叠前深度偏移的不断发展,特别是逆时偏移(Baysal E, and Kosloff D D et al,1983;McMechan G A 1983;Whitmore,N.D 1983)在计算性能和存储能力大幅提高的推动下,迅速发展成熟并得到较广泛的应用(Gray S.H. and Marfurt K.J,1995;Raiaskaran S. and McMeehan G A,1995;Larry Lines et al,1996;Yoon K and Marfurt K J,2004;Symes W W,2007;Zhang Y et al,2007;Clapp R G,2009;赵磊等,2010;刘定进等,2011;孔祥宁等,2013),复杂构造成像问题找到了较好的解决途径.然而,因地表起伏引起的道间时差问题依然是一个突出瓶颈.在常规地震资料处理与成像中,通常基于地表一致性假设采用基准面静校正的办法解决道间时差的影响.但是,在地表起伏剧烈且横向速度变化剧烈、地表速度高的地区,地表一致性假设不再成立,静校正会使地震记录发生畸变扭曲,采用“静校正+固定面偏移”的成像流程无法很好地解决复杂地表条件下的地震成像问题.
基于地表进行偏移是解决复杂地表成像问题的一个有效途径.Wiggins(1984)提出了非水平地震数据的Kirchhoff积分法延拓和偏移方法;Gray和Marfurt(1995)将基于地表的Kirchhoff叠前深度偏移应用于加拿大山地模型数据成像,显著改善了浅层成像质量;Raiaskaran和McMeehan(1995)以及Lines等(1996)介绍基于地表的逆时偏移方法和应用效果.在国内,朱海波等(2012),孔祥宁等(2013)给出了一套起伏地表叠前时间偏移处理流程及其应用效果;刘少勇和王华忠(2010)研究了起伏地表Kirchhoff叠前深度偏移方法,认为应当选择适当光滑的成像基准面来消除或减弱高波数道间时差对叠前成像的影响,并提出了一套起伏地表条件下的Kirchhoff积分法叠前深度偏移处理流程;刘红伟等(2011)、王延光(2012)介绍了起伏地表叠前逆时偏移技术,以起伏地表模型数据为例展示了起伏地表逆时偏移方法的成像效果.本文借鉴文献(刘少勇和王华忠等, 2010)关于消除高波数道间时差的思想,提出结合常规地震数据处理的逆时偏移成像技术流程,并应用到模型数据和实际资料的成像处理中.
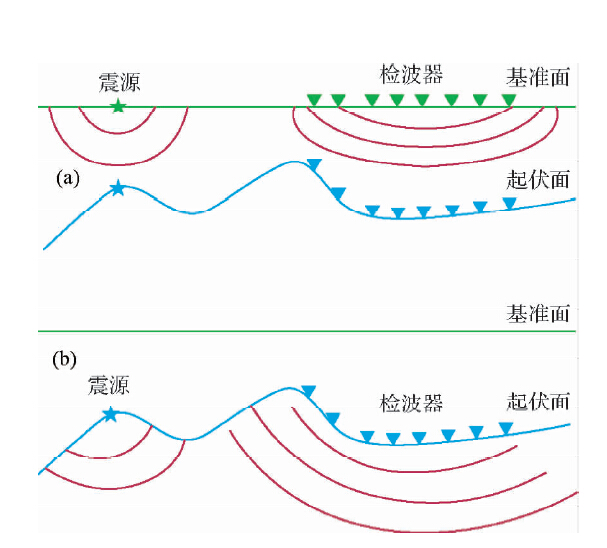 | 图 1 固定面逆时偏移(a)与起伏面逆时 偏移(b)示意图 Fig. 1 The diagram of RTM from fixed datum(a) and RTM from rugged datum(b) |
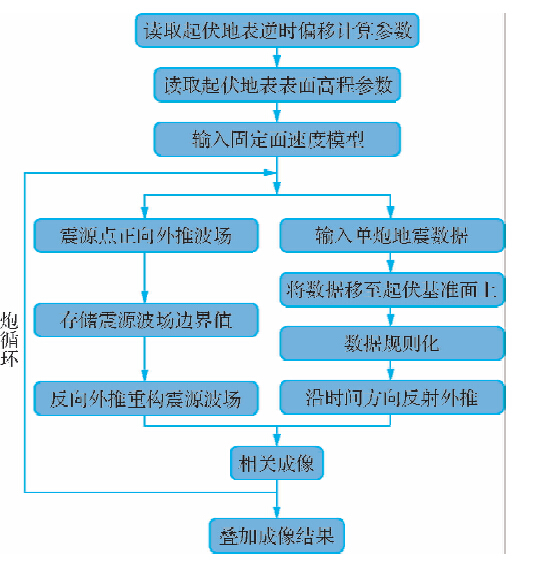 | 图 2 基于起伏面的逆时偏移流程图 Fig. 2 The flow of reverse time migration from rugged datum |
弱散射假设下,地表 r g处接收到的地震数据在频域内表示为(Gray S.H et al,1995)
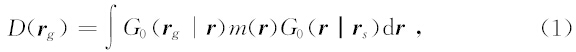
将正演模拟算子的伴随矩阵作用于地震数据,代表地震偏移成像过程(Raiaskaran S et al,1995),成像值为
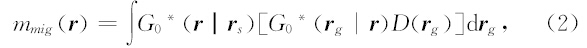
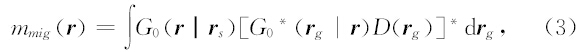
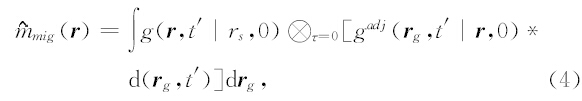
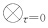 表示正传信号与反传信号进行零延迟互相关,它是一个对时间的积分.以上为逆时偏移的基本原理.在逆时偏移实现过程中,通常基于波动方程的微分解利用有限差分算法实现地震波场的正向传播与逆向传播.
表示正传信号与反传信号进行零延迟互相关,它是一个对时间的积分.以上为逆时偏移的基本原理.在逆时偏移实现过程中,通常基于波动方程的微分解利用有限差分算法实现地震波场的正向传播与逆向传播.基于起伏面的逆时偏移与固定面逆时偏移的基本理论一致,正演模拟波场传播算法也相同.两者差别在于后者的炮点、接收点都位于固定面上,或者被校正到固定面上(图 1a),而前者的炮点、接收点则位于接近于真地表的起伏面上(图 1b).为简单起见,起伏面逆时偏移中波场模拟计算网格和速度模型仍然是规则立方体,炮点、接收点位于立方体内部,炮点与接收点以上部分没有考虑真实的边界情况.
2 技术流程叠前偏移成像需要基于常规处理后的地震数据,结合起伏面逆时偏移算法实现方式,我们形成基于起伏面的逆时偏移技术流程,内容如下:
(1)常规预处理,数据校正到固定基准面.
(2)在平滑起伏面进行速度分析和速度建模,在固定面与起伏面之间填充替换速度,获得基于固定面的深度域速度模型.
(3)进行起伏面逆时偏移.利用固定面与起伏面高程差和替换速度将固定面地震数据时移到起伏基准面上,本时移过程相当于反静校正,去掉低频静校正量,仅保留高波数静校正量;利用固定面速度模型进行震源正向传播和地震数据逆向传播,炮点和接收点位于起伏面上,利用互相关成像条件提取成像值.本步骤实现流程如图 2所示.与传统固定面逆时偏移不同的是,起伏面逆时偏移要将输入的静校正后的数据通过时移返还到起伏面上,在起伏面进行波场的正向传播和逆向传播,而固定面逆时偏移则直接假定震源和检波点位于同一顶面上,从该基准面开始波场传播.
(4)对偏移叠加数据体做laplace滤波,去除逆时偏移的低频噪音.
3 模型试验与实际应用 3.1 起伏地表模型该模型由Amoco和BP公司设计,速度场如图 3所示,其地质原型为加拿大英属哥伦比亚东北部的逆掩断层构造.该模型地表起伏变化大,地形最大高差达1527 m,地表横向速度变化剧烈.地震炮记录由SEG/EAGE提供,共278炮,每炮最大道数为480道,时间采样点2000,采样率4 ms,道间距15 m,最小偏移距15 m,最大偏移距3600 m,炮间距90 m.
图 4a是某一炮原始地震记录,图 4b是静校正后的该炮记录,可见一些不规则的时距曲线经静校正后近似双曲线形状.对静校正的该炮地震数据进行逆时偏移,图 5a是固定面偏移结果,图 5b是起伏面偏移结果.需要指出,由于速度精确模型已知,静校正时不存在高频静校正量与低频静校正量之别,因此起伏面偏移基于真地表,而没有必要选择平滑起伏面.由图 5可见,固定面偏移中波场从地表开始传播,与真实的波传播过程存在较大差异,造成波场扭曲,从而使得偏移成像效果较差.图 6是加拿大起伏地表模型278炮数据的逆时偏移成像结果,偏移后采用laplace滤波去除了逆时偏移低频噪音,并沿地表做了地表高程以上剖面切除.分析图 6a固定面偏移结果与图 6b起伏面偏移结果,可见固定面偏移波场收敛较差,同相轴连续性不好、剖面整体信噪比低,浅层尤为严重,中浅层构造形态与真实速度模型存在较大差异,而起伏面偏移效果远好于固定面偏移,构造形态与真实速度模型一致.
3.2 实际资料成像某实际陆地三维地震工区位于西亚库尔德斯坦地区,地表以山丘为主,分布有耕地、沙漠和草地等,起伏不平,最大地形高差为700多米.现有的地震资料和微测井资料均表明该区近地表速度变化大,存在严重的静校正问题.该处存在NW-SE向背斜构造,裂缝发育,主要含油层系为中生界白垩系的三套地层,埋深约为1000~1800 m,储层厚度达500 m.由模型数据偏移结果可知,相对于固定面逆时偏移而言,起伏面逆时偏移的浅层成像效果有很大改善.因此,考虑到该工区目的层较浅,我们将起伏面逆时偏移应用到该工区的成像处理中.
在平滑起伏面上进行地震资料常规预处理和速度建模,把预处理后的叠前炮集数据校正到一个固定基准面,并利用替换速度获得固定面深度域速度模型.由叠前炮集数据和深度域速度模型,分别进行了固定面逆时偏移和起伏面逆时偏移.叠前逆时偏移计算采用25.0 m×25.0 m的面元网格,最大成像深度为10000 m,深度延拓步长为8 m,为了满足陡构造的成像要求,成像计算时采用的单边偏移孔径为6000.0 m×6000.0 m,x,y方向的吸收边界厚度均为500 m,子波频率为40.0 Hz,时间延拓长度为6.0 s,时间延拓步长为0.5 ms.使用60个计算节点,每个节点两块NVIDIA Tesla M2090 GPU卡,单炮用时约为20 min.总成像范围为Ny=1000(dy=25.0 m),Nx=650(dx=25.0 m),Nz=1251(dz=8.0 m)面积:406 km2(满覆盖210 km2),共10206炮,总用时为3天.
图 7是静校正后的一炮地震数据,图 8a和图 8b分别是该炮固定面偏移剖面和起伏面偏移剖面,易见固定面偏移从静校正后的基准面开始传播波场,而起伏面偏移从基准面下的真实炮检点位置开始传播波场.图 9是所有炮偏移成像结果,偏移后做了laplace滤波处理.可以看出,起伏面逆时偏移剖面的浅层同相轴连续性更好,剖面信噪比更高,波组强弱特征更加明显.
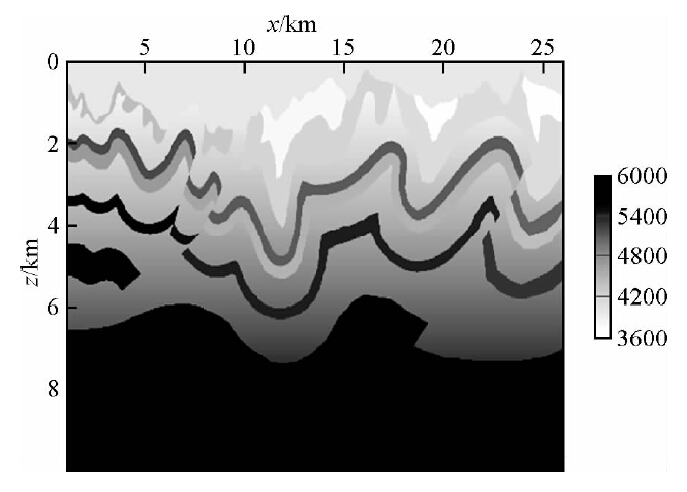 | 图 3 加拿大起伏地表模型 Fig. 3 Canada rugged topography model |
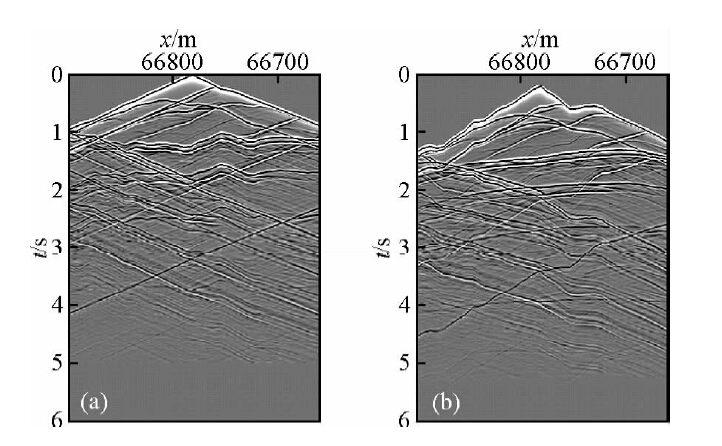 | 图 4 某炮原始记录(a)与静校正后记录(b) Fig. 4 The original shot gather(a) and the shot gather after static correction(b) |
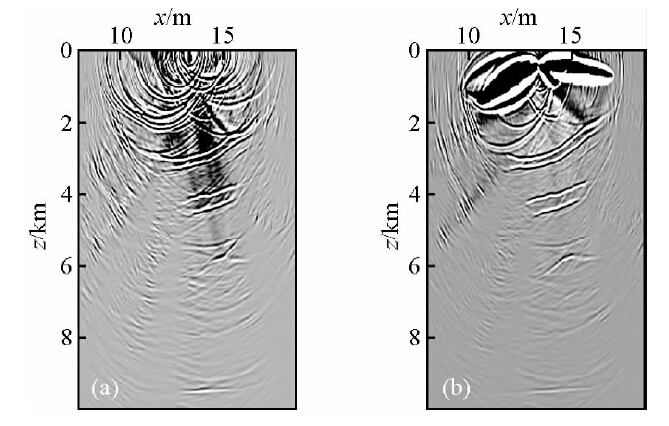 | 图 5 某炮固定面逆时偏移(a)与起伏面逆时 偏移(b)结果 Fig. 5 The result of RTM from fixed datum(a) and RTM from rugged datum(b)by one shot |
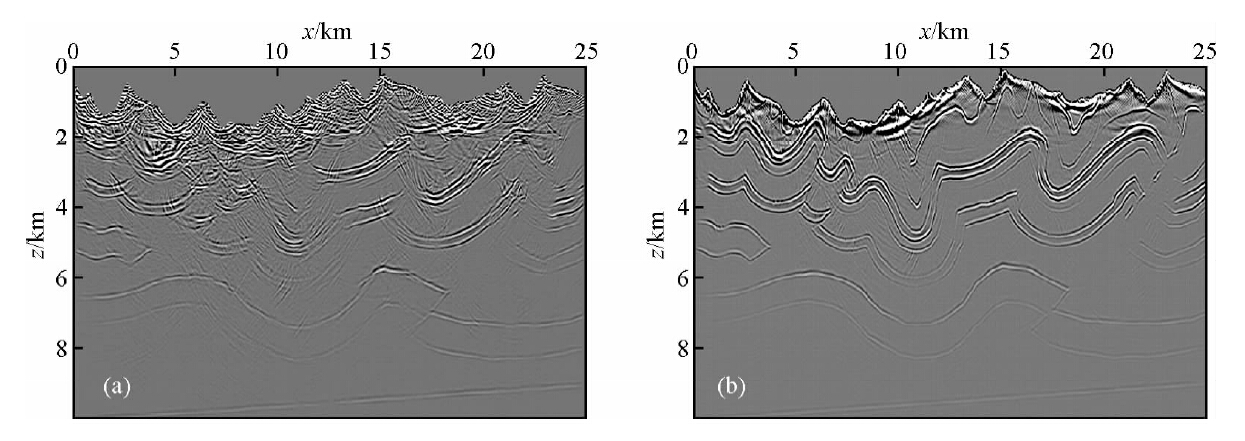 | 图 6 加拿大模型固定面逆时偏移(a)与起伏面逆时偏移(b)结果 Fig. 6 The result of RTM from fixed datum(a) and RTM from rugged datum(b)on Canada model |
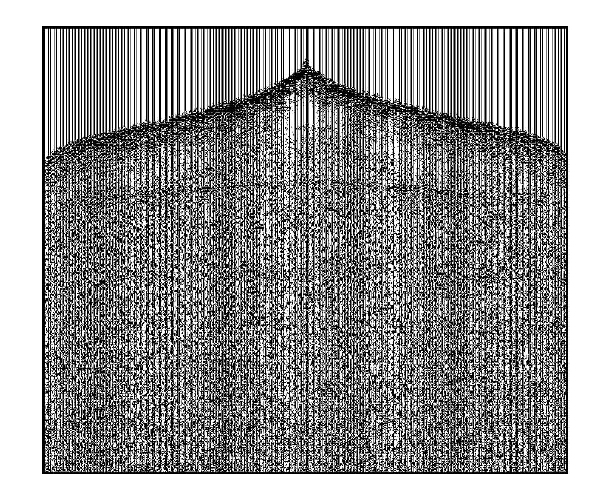 | 图 7 静校正后的炮集记录 Fig. 7 The shot gather after static correction |
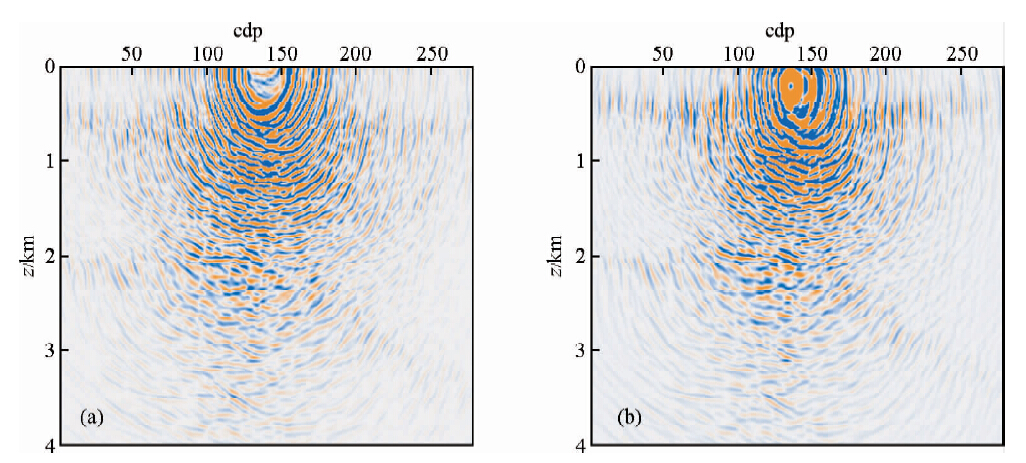 | 图 8 某炮固定面逆时偏移(a)与起伏面逆时偏移(b)结果 Fig. 8 The result of RTM from fixed datum(a) and RTM from rugged datum(b)by one shot |
 | 图 9 所有炮固定面逆时偏移(a)与起伏面逆时偏移(b)结果 Fig. 9 The result of RTM from fixed datum(a) and RTM from rugged datum(b)by all shot gathers |
结合地震资料常规处理流程,本文介绍了一种基于起伏面的逆时偏移成像技术.输入静校正后的叠前地震数据和固定面深度域速度模型,利用固定面与起伏面高程差和替换速度可以进行起伏面逆时偏移.模型数据和实际资料均表明,相对于固定面逆时偏移而言基于起伏面的逆时偏移成像效果更好,同相轴连续性更好,剖面信噪比更高,浅层尤为明显.
致 谢 论文得到了中国石化石油物探技术研究院及同济大学WPI课题组的大力支持,在此对其表示衷心的感谢.另外,非常感谢审稿专家对本文的指导和建议.
| [1] | Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11):1514-1524. |
| [2] | Clapp R G. 2009. Reverse time migration with random boundaries. Expanded Abstracts of 79 th Annual International Meeting, SEG, 2809-2812. |
| [3] | Gray S.H.,Marfurt K.J. 1995. Migration from topography:Improving the near-surface image. Canadian Journal of Exploration Geophysics, 31(1):18-24. |
| [4] | Kong X N, Zhang H Y, Liu S W,et al. 2013. Multi-GPUs parallel computational stratery of prestack reverse-time migration for mass seismic data. Geophysical Prospecting for Petroleum, 52(5):288-293. |
| [5] | Kong X N, Zhu H B. 2013. Application study of topography pre-stack migration in YCN area. Progress in Geophys.(in Chinese), 28(3):1390-1397. |
| [6] | Larry Lines,Wenjing Wu,Hanxing Lu, et al. 1996. Migration from topography: Experience with an Alberta Foothills dataset. Canadian Journal of Exploration Geophysics, 32(1):24-30. |
| [7] | Liu D J, Yang Q Y, Fang W B,et al. 2011. Realization and Practices of prestack reverse-time depth migration. Geophysical Prospecting for Petroleum, 50(6): 545-549. |
| [8] | Liu H W, Liu H, Li B,et al. 2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology. Chinese J.Geophys. (in Chinese), 54(7):1883-1892. |
| [9] | Liu S Y, Wang H Z, Zhang B. 2010. Kirchhoff Integral PSDM for Rugged Topography:Technology and Applications. Lithologic Reservoirs, 7:49-54. |
| [10] | McMechan G A. 1983. Migration by extrapolation of time-dependent boundary values. Geophysical Prospecting, 31(3): 413-420. |
| [11] | Raiaskaran S.,McMeehan G A. 1995. Prestack processing of land data with complex topography. Geophysics, 60(6):1875-1886. |
| [12] | Symes W W.2007. Reverse time migration wit h optimal checkpointing. Geophysic , 72 (5):SM213-SM221. |
| [13] | Wang Y G,Kuang B.2012.Prestack reverse-time depth migration on rugged topography and parallel computation realization.Oil Geophysical Prospecting,47(2):266-271. |
| [14] | Whitmore,N.D. 1983. Iterative Depth Migration by Backward Time Propagation. Expanded Abstracts of 53nd Annual International Meeting, SEG , 382-385. |
| [15] | Yoon K, Marfurt K J, Starr W. 2004. Challenges in reverse-time migration. Expanded Abstracts of 74th Annual International Meeting, SEG, 1057-1060. |
| [16] | Zhang Y, Sun J, Gray S. 2007. Reverse-time migration: amplitude and implementation issues. Expanded Abstracts of 77th Annual International Meeting, SEG, 2145-2149. |
| [17] | Zhang Y, Sun J. 2009. Practical issues in reverse time migration: true amplitude gathers, noise removal and harmonic source encoding. First Break, 26(1):29-35. |
| [18] | Zhao L, Wang H Z, Liu S W. 2010. Reverse-time Depth Migration Imaging and Its Application at CPU/GPU Platform. Lithologic Reservoirs, 22(F07):36-41. |
| [19] | Zhu H B, Lin B X, Xu Z T,et al. 2012. Prestack time migration scheme from rugged topography and its application. Geophysical Prospecting for Petroleum, 51(5):486-492. |
| [20] | 孔祥宁,张慧宇,刘守伟,等. 2013. 海量地震数据叠前逆时偏移的多GPU联合并行计算策略. 石油物探, 52(5):288-293. |
| [21] | 孔祥宁,朱海波. 2013. 起伏地表叠前偏移在YCN探区的应用研究.地球物理学进展. 28(3):l390-1397. |
| [22] | 刘定进,杨勤勇,方伍宝,等. 2011. 叠前逆时深度偏移成像的实现与应用. 石油物探, 50(6): 545-549. |
| [23] | 刘红伟,刘洪,李博,等. 2011. 起伏地表叠前逆时偏移理论及GPU加速技术. 地球物理学报. 54(7):1883-1892. |
| [24] | 刘少勇,王华忠,张兵. 2010. 起伏地表Kirchhoff积分法叠前深度偏移方法研究与应用. 岩性油气藏, 7:49-54. |
| [25] | 王延光,匡斌. 2012. 起伏地表叠前逆时深度偏移与并行实现. 石油地球物理勘探, 47(2):266-271. |
| [26] | 朱海波,林伯香,徐兆涛,等. 2012. 起伏地表叠前时间偏移处理流程及其应用研究. 石油物探, 51(5):486-492. |
| [27] | 赵磊,王华忠,刘守伟. 2010. 时深度偏移成像方法及其在逆CPU/GPU异构平台上的实现.岩性油气藏,22(F07):36-41.. |
 2014, Vol. 29
2014, Vol. 29

